Eventos de crecidas extraordinarias en el Rio San Pedro

Encuentro Internacional de Manejo del Riesgo por Inundaciones
Eventos de crecidas extraordinarias en el Rio San Pedro‐Mezquital, Nayarit, Mexico
Luis Brito Castillo
CIBNOR, SC ‐ REDESClim
21 – 24 de enero de 2013
Instituto de Ingeniería, UNAM, Ciudad Universitaria, México, D.F.
E‐mail: lbrito04@cibnor.mx
Dr. David Gochis, NCAR, Boulder Colorado, USA
Dr. Enrique Vivoni, University of Arizona, USA
Prof. Alexander Zolotokrylin, Instituto de Geografìa, Academia de Ciencias Rusa
Dra. Iryna Tereshchenko, Universidad de Guadalajara
Dr. Emilio Palacios, Universidad de Guadalajara
Dr. Anatoliy Filonov, Universidad de Guadalajara
Dr. Oscar Gutierrez Ruacho, CESUES, Sonora
Alumnos
Jose Pablo Vega Camarena
Rodolfo Jofre
Susana Dominguez
Mayra Gaxiola
Marcos Alberto Rodriguez Najera
Julio Cesar Zamora Valenzuela
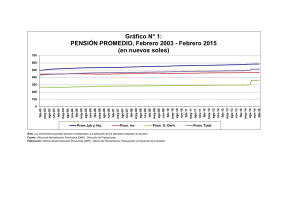
Distribución de la lluvia
Media diaria por mes
Brito‐Castillo, 2012. INTECH, cap. 18.
CONTENIDO
• Antecedentes de investigación
– Variabilidad climática vs. Cambio climático
– Zona climatológicamente anómala
• Importancia e interés de la cuenca del río San Pedro Mezquital
• Características y aforos
• Análisis de gastos máximos
• Análisis de frecuencias
• Conclusiones
Variabilidad climática vs. Cambio climático
TEMPERATURAS
Prom = Cte.
Enfriamiento paulatino
(Tendencia negativa)
Oscilación de baja frecuencia
SALTO REPENTINO
Prom 1 = Cte.
Prom 2 = Cte.
Borroughs, 2008
Hay dos enfoques para detectar los cambios en los recursos hídricos:
1. Analizando los cambios observados en los componentes del balance hídrico
(entendiendo el CICLO HIDRO-ILÓGICO)
2. El análisis de tendencias
Ambos enfoque son difíciles de llevar a la práctica
En el primer caso, se espera que el incremento de la temperatura global provoque perturbaciones en el ciclo del agua, pero los cambios son extremadamente difíciles de detectar. Algunos componentes ni siquiera los podemos medir, son estimaciones, ejem, las pérdidas por evapotranspiración.
En el segundo caso, se hace necesario contar con series suficientemente largas, homogéneas y representativas de una región (falta de datos)
Aún cuando se observan tendencias de algún tipo, su correcta interpretación no es sencilla, hay dificultades al intentar atribuir los cambios a perturbaciones antropogénicas como la sobreexplotación de acuíferos, los desvíos de agua para irrigación, el control del agua para generación de energía eléctrica y control de avenidas, y la complejidad de los procesos que externamente forzan la variabilidad hidroclimática (cambios naturales y variabilidad intrínseca de baja frecuencia)
El ajuste lineal:
Yest = a + bT,
donde
b = [Σ{(Ti - Tavg)(Yi - Yavg)}] / [Σ{(Ti - Tavg)²}], pendiente de la recta
T = tiempo (predictor, variable indpendiente)
Y = Serie problema (criterio, variable dependiente)
Σ = sumatoria de i = 1….n;
est y avg = subíndices, serie estimada y valor promedio respectivamente
No siempre es adecuado, particularmente cuando la serie muestra variabilidad
interanual sobrepuesta a variabilidad de baja frecuencia (medida en décadas).
El ajuste de la línea de tendencia se estima como:
Var (b) = (SE)² = MSE/ [Σ{(T - Tavg)²}]
MSE = [Σ{(Y - Yest)²}] / (n - 2)
MSE y SE son error medio cuadrado y desviación estándar, respectivamente. Entre
más pequeños sean, mejor el ajuste.
Ejemplos:
Línea oscura, ajuste de tendencia lineal por el método de mínimos cuadrados.
± = define el intervalo de confianza de la tendencia al 95%
Número de días en el año con
precipitación diferente de cero
Precipitación acumulada anual
Caudal medio anual
En las tres series se observa un incremento general. Un análisis detallado muestra mejor la estructura de las series, hasta 1959, las series muestran un decremento y posterior a ese año un incremento. Procesos no lineales.
Correspondencia en las tendencias observadas en lluvias y caudales,
Ejemplo: cuenca del río Lerma (Caudal medio anual Vs. lluvia acumulada y número de días en
el año con lluvia diferente de cero)
Estaciones al interior
de la cuenca
Climatológica
DP: Número de días
con registro de lluvia
diferente de cero
VP: lluvia acumulada
Climatológica
Hidrométrica
Q: Caudal medio
RESULTADOS ( tendencias observadas en precipitación acumulada)
RESULTADOS (tendencias observadas en caudales medios)
Referencias
Brito‐Castillo et al., 2010. J. Arid. Environ., 74(5): 531‐539;
Palacios‐Hernández et al., 2010.
Ocean Dynamics, 60: 81‐90
Palacios‐Hernández et al., 2012. Atmósfera, 25(4): 335‐370
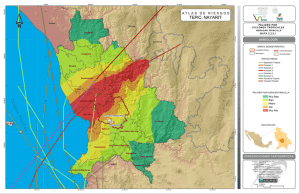
LA CUENCA DEL RÍO SAN PEDRO‐MEZQUITAL
Cuenca hidrológica del río San Pedro-Mezquital
Características
Aaforada = 25,800 KM²
Lsección = 340 m
Lcauce = 255 km
Esviajamiento = 20°
Aforos
Se realizan con Molinete
Lietz, Tamaya y Gurley
(02 de nov. de 1944)
Registro gráfico de niveles con limnígrafo Stevens tipo E (07 de marzo de 1948)
Periodo 1944‐2006
Qmax = 6300 m³/s (Sep 93)
Qmin = 0.210 m³/S (Jul 67)
Qavg_an = 1850 m³/s
Qavg_smr = 1570 m³/s
Qavg_wnt = 750 m³/s
Nos propusimos analizar los hidrogramas observados resultantes de crecidas extraordinarias y para cada evento determinar, el gasto pico, el tiempo de crecimiento de la crecida y la duración total.
METODOLOGIA
Selección de eventos de crecidas extraordinarias a partir de datos horarios (BANDAS)
Estimación de las caracteristicas de cada evento
Separación de crecidas de invierno y de verano
Ajuste de una distribución de probabilidades para series de maximos anuales, maximos
de verano y maximos de invierno
Nombre
Acrónimo
Referencia
Normal
(N)
(Gauss)
Log‐normal
(LN)
(Hazen, 1914)
Pearson tipo 3
(P3)
(Foster, 1924)
Valores extremos tipo 1
(EV1)
(Gumbel, 1941)
Valores extremos tipo 2
(EV2)
(Gumbel, 1941)
Valores extremos tipo 3
(EV3)
(Jenkinson, 1969)
Distribución gamma de 3 parametros
(Kritsky, Menkel, 1946)
Gamma
(G)
(Moran, 1957)
Log‐Pearson tipo 3
(LP3)
(U.S. Water Resources Council, 1967)
Weibull
(Wu et Goodbridge, 1976)
Boughton
(Boughton, 1980)
Análisis de gastos máximos horarios
Tr=20
N
Año
Mes
Día
Hora
Gasto m³/s
1
1957
10
22
05
4790
2
1968
09
14
00
4800
3
1969
10
12
14
4020
4
1972
11
24
18
5050
5
1976
11
28
14
5120
6
1985
01
14
06
4120
7
1993
09
13
23
6300
8
1994
10
14
19
4850
9
2003
09
22
01
4550
Ajuste de una distribución de probabilidades
DISTRIBUCIÓN DE PEARSON TIPO III
VERANO: media = 1576 m³/s; Cv = 2.13; n = 62
P
0.01
0.1
1
3
5
10
Q
11888
8943
6016
4652
4024
3134
INVIERNO: media = 736 m³/s; Cv = 2.39; n = 61
P
0.01
0.1
1
3
5
10
Q
11022
8017
5058
3710
3026
2168
CONCLUSIONES
N
Año
Gasto, m³/s
Tr=1/p
T, hr
D, hr
Causa
1
1957
4792
30
14
34
17‐21/oct/ Huracan‐1
2
1968
4800
30
22
71
09‐13/sep/ Huracan‐1
3
1969
4016
20
24
44
09‐12/oct/ Huracan‐1
4
1972
5045
100
24
48
5
1976
5122
100
37
67
6
1985
4125
30
7
61
7
1993
6302
100
28
65
08‐14/sep/ LIDIA CAT. 4
8
1994
4847
30
18
43
08‐15/oct/ ROSA CAT. 2
9
2003
4553
30
17
70
19‐24/oct/ MARTY CAT. 2
4840
50
21
56
Prom.
http://weather.unisys.com/hurricane/index.php
‐ La duración de la creciente hasta alcanzar el pico máximo es mayor de 6 hrs
‐ Se observa una intercalación de picos máximos entre verano e invierno, en diferentes periodos. GRACIAS!
AGRADECIMIENTOS
INEGI
Instituto de Geofísica de la UNAM
CIBNOR SC, Unidad Sonora, campus Guaymas
REDESClim (CONACYT)