Optimización. E: Halle el punto de la recta y = mx + b más cercano al
Anuncio

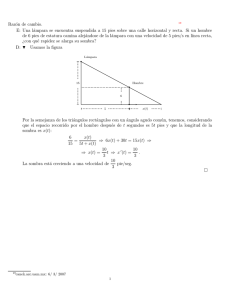
Optimización. E: Halle el punto de la recta y = mx + b más cercano al origen. 25 D: H y = mx + b Un punto arbitrario sobre la recta tiene las coordenadas (x, mx + b). Distancia de un punto de la recta al origen. p d = x2 + (mx + b)2 • Vamos a trabajar con el cuadrado de la función anterior. Tiene los mismos puntos crı́ticos. Usaremos la notación D = d2 D = x2 + (mx + b)2 D 0 = 2x + 2(mx + b)m D 00 = 2 + 2m2 > 0 Segunda derivada siempre positiva 2x + 2(m2 x + bm) = 0 ⇒ x + m2 x + bm = 0 ⇒ x(1 + m2 ) = −bm ⇒ xM in = − bm 1 + m2 Mı́nimo absoluto yM in = m(− bm −bm2 −bm2 + b + bm2 b ) + b = + b = = 1 + m2 1 + m2 1 + m2 1 + m2 Ası́ xM in = −myM in El punto deseado sobre la recta es : (xM in , yM in ) = bm b − , 2 1 + m 1 + m2 25 canek.azc.uam.mx: 6/ 3/ 2007 1