1. Construcción de la Integral
Anuncio
1. Construcción de la Integral
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
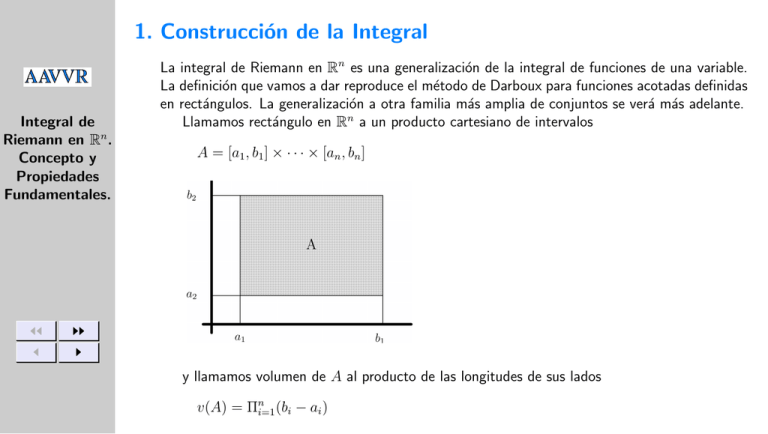
La integral de Riemann en Rn es una generalización de la integral de funciones de una variable.
La definición que vamos a dar reproduce el método de Darboux para funciones acotadas definidas
en rectángulos. La generalización a otra familia más amplia de conjuntos se verá más adelante.
Llamamos rectángulo en Rn a un producto cartesiano de intervalos
A = [a1 , b1 ] × · · · × [an , bn ]
y llamamos volumen de A al producto de las longitudes de sus lados
v(A) = Πni=1 (bi − ai )
Llamamos partición de A a una familia P formada por una partición de cada uno de los
intervalos, P = {P1 , . . . , Pn }, donde Pi = {a = t0 ≤ · · · ≤ tki = bi } es una partición de [ai , bi ]
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Una partición P de A define una familia finita de rectángulos, que llamaremos RP , que verifica
[
X
A=
R; v(A) =
v(R)
R∈RP
JJ
II
J
I
R∈RP
Si P = {P1 , . . . , Pn } y Q = {Q1 , . . . , Qn } son dos particiones de A, se dice que Q ≥ P , o
que Q es más fina que P , si para cada i entre 1 y n Pi ⊆ Qi . En este caso, Q define en cada
rectángulo R de RP una partición QR .
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Dadas dos particiones P y Q de A, llamaremos P ∪ Q a la partición formada por todos los
puntos de cada Pi y Qi
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Definición (Sumas de Riemann).
Sea f : A −→ R una función acotada, y P una partición de A. Para cada rectángulo R ∈ RP
se definen:
mR (f ) = inf{f (x); x ∈ R}
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
MR (f ) = sup{f (x); x ∈ R}
Se definen la Suma Inferior de Riemann y la Suma Superior de Riemann por
X
mR (f ) v(R)
S(f, P ) =
R∈RP
S(f, P ) =
X
R∈RP
respectivamente.
JJ
II
J
I
MR (f ) v(R)
Si f es una función no negativa, S(f, P ) es la suma de los volúmenes de los rectángulos
R × [0, mR (f )], levantados por debajo de la gráfica de f , y S(f, P ) es la suma de los volúmenes
de los rectángulos R × [0, MR (f )] construidos por encima de la gráfica de f
Caso n=1:
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Caso n=2
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Estas sumas superiores e inferiores verifican las siguientes propiedades:
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Estas sumas superiores e inferiores verifican las siguientes propiedades:
1.- Para toda partición P de A,
S(f, P ) ≤ S(f, P )
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
2.- Si P y Q son dos particiones con P ≤ Q, entonces
S(f, P ) ≤ S(f, Q)
y
S(f, P ) ≥ S(f, Q)
es decir, cuanto más fina es la partición, la suma inferior es mayor y la superior es menor.
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
t0
t1
t2
t3
t4
t5
s0 s1 s2 s3 s4 s5 s6 s7 s8 s9 s10
P ≤Q
P = {t0 , t1 , t2 , t3 , t4 , t5 }
JJ
II
J
I
S(f, P )
Q = {s0 , s1 , s2 , s3 , s4 , s5 , s6 , s7 , s8 , s9 , s10 }
S(f, Q)
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
t0
t1
t2
t3
t4
t5
s0 s1 s2 s3 s4 s5 s6 s7 s8 s9 s10
P ≤Q
P = {t0 , t1 , t2 , t3 , t4 , t5 }
S(f, P )
Q = {s0 , s1 , s2 , s3 , s4 , s5 , s6 , s7 , s8 , s9 , s10 }
S(f, Q)
JJ
II
J
I
3.- Para toda partición P de A,
mA (f )v(A) ≤ S(f, P ) ≤ S(f, P ) ≤ MA (f )v(A)
MA (f )v(A)
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
S(f, P )
S(f, P )
t0
t1
t2
t3
t4
t5
mA (f )v(A)
P = {t0 , t1 , t2 , t3 , t4 , t5 }
JJ
II
J
I
4.- Si P y Q son dos particiones cualesquiera de A,
S(f, P ) ≤ S(f, Q)
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
t0
t1
t2
t3
t4
t5
s3
s4
s5 s6
s0 s1
s2
P = {t0 , t1 , t2 , t3 , t4 , t5 }
JJ
II
J
I
S(f, P )
Q = {s0 , s1 , s2 , s3 , s4 , s5 , s6 }
S(f, Q)
Definimos ahora las integrales inferior y superior de una función de la siguiente manera:
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Definición (Integral Superior e Integral Inferior).
Sea A un rectángulo en Rn , y f : A −→ R una función acotada.
Se llama integral inferior de f en A a
Z
f = sup{S(f, P ); P partición de A}
A
Y se llama integral superior de f en A a
Z
f = inf{S(f, P ); P partición de A}
A
JJ
II
J
I
Las integrales superior e inferior están bien definidas, en el sentido de que como los conjuntos
de sumas superiores e inferiores de Riemann de f son acotados, existen el supremo y el ı́nfimo
respectivamente.
Además, por las propiedades que hemos visto antes, se tiene que
Z
Z
mA (f )v(A) ≤
f≤
f ≤ MA (f )v(A)
A
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
Definición (Función Integrable Riemann).
Sea A un rectángulo en Rn , y f : A −→ R. Se dice que f es integrable Riemann en A si es
acotada y las integrales superior e inferior de f en A coinciden. En este caso se llama integral
de f en A a
Z
Z
Z
f
f=
f=
A
A
A
Ejemplo 1. Toda función
Z constante en un rectángulo es integrable. Además, si f (x) = a para
f = av(A)
cada x ∈ A, entonces
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
En efecto, si P es una partición cualquiera de A, y R es uno de los rectángulos definidos por
P , mR (f ) = a = MR (f ), ası́ que
X
X
X
S(f, P ) =
MR (f )v(R) =
av(R) = a
v(R) = av(A)
R∈RP
R∈RP
R∈RP
y
S(f, P ) =
X
R∈RP
mR (f )v(R) =
X
av(R) = a
R∈RP
X
v(R) = av(A)
R∈RP
Por tanto
Z
f = inf{S(f, P ), P partición de A} = av(A)
A
y
JJ
II
J
I
Z
f = sup{S(f, P ), P partición de A} = av(A)
A
Z
las dos integrales son iguales, f es integrable, y
f = av(A)
A
Ejemplo 2. La función de Dirichlet, f : [0, 1] −→ R definida por
1
si x ∈ Q
f (x) =
0
si x 6∈ Q
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
no es integrable Riemann.
En efecto, si P es una partición cualquiera de A, y R es uno de los rectángulos definidos por
P , en R habrá números racionales y números irracionales, de modo que mR (f ) = 0 y MR (f ) = 1,
ası́ que
X
X
S(f, P ) =
MR (f )v(R) =
v(R) = v([0, 1]) = 1
R∈RP
R∈RP
y
S(f, P ) =
X
mR (f )v(R) = 0
R∈RP
Por tanto
Z
JJ
J
f = inf{S(f, P ), P partición de A} = 1
II
I
A
y
Z
f = sup{S(f, P ), P partición de A} = 0
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Ejemplo 3. Funciones no integrables en R2
Partiendo del ejemplo anterior, es fácil construir funciones que no sean integrables, definidas
en conjuntos de R2 , o en general de Rn . Por ejemplo, puede ser
1
si x ∈ Q
f (x, y) =
0
si x 6∈ Q
definida en A = [0, 1] × [0, 1], o
g(x, y) =
1
0
si
si
(x, y) ∈ Q2
(x, y) 6∈ Q2
JJ
II
J
I
2. Criterio de Riemann
El primer teorema que vamos a demostrar, da una condición equivalente para la integrabilidad de
una función, aunque no da el valor de su integral. Es una condición parecida a la condición de
Cauchy de las sucesiones de números reales, o de vectores de Rn .
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Teorema (Criterio de Integrabilidad de Riemann).
Sea A un rectángulo en Rn, y f : A −→ R una función acotada en A.
f es integrable en A si y sólo si para cada > 0 existe una partición
P de A tal que
S(f, P) − S(f, P) ≤ JJ
II
J
I
Demostración:
I (Saltar al final de la demostración)
Supongamos primero que f es integrable en A, y sea > 0. Por la definición de la integral
superior como el ı́nfimo de
R las sumas superiores de Riemann, existirá al menos una partición P1
de A tal que S(f, P1 ) < A f + /2. Y por la definición de la integral inferior como
R supremo de
f − /2.
las sumas inferiores, existirá al menos una partición P2 de A tal que S(f, P2 ) >
A
Consideramos entonces la partición P unión de P1 y P2 , y tenemos
Z
S(f, P ) ≤ S(f, P1 ) <
f + /2
A
y
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Z
S(f, P ) ≥ S(f, P2 ) >
f − /2
A
de donde restando las dos desigualdades se obtiene
Z
Z
S(f, P ) − S(f, P ) <
f + /2 −
f + /2 = A
A
Z
Z
f=
ya que por ser f integrable
A
JJ
II
J
I
f.
A
Recı́procamente, supongamos ahora que para cada > 0 existe alguna partición P de A tal
que S(f, P ) − S(f, P ) < Z
Z
Entonces como
f ≤ S(f, P ) y
f ≥ S(f, P ), tenemos
A
Z
A
Z
0≤
f−
A
f ≤ S(f, P ) − S(f, P ) < A
y esto para todo > 0, luego necesariamente
Z
Z
f=
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
f
A
y por tanto f es integrable en A.
J(Volver al enunciado)
Como consecuencia de este teorema es fácil demostrar que toda función continua en un
rectángulo es integrable, o incluso que toda función monótona es integrable (ver problemas)
3. Propiedades
Para terminar este primer capı́tulo, vamos a demostrar las propiedades elementales de la integral
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Teorema (Propiedades de la Integral de Riemann).
Sea A un rectángulo en Rn , y sean f : A −→ R y g : A −→ R dos funciones integrables en A.
R
R
R
1. la suma f + g es integrable y A (f + g) = A f + A g
R
R
2. para todo α ∈ R el producto αf es integrable, y A (αf ) = α A f
Z
3. si f ≥ 0, entonces
f ≥0
A
Z
4. si f ≥ g, entonces
Z
f≥
A
5. |f | también es integrable, y
JJ
II
J
I
g
A
Z Z
f ≤
|f |
A
6. max{f, g} y min{f, g} son integrables
7. el cuadrado f 2 es integrable
8. el producto f g es integrable
A
I (Saltar al final de la demostración)
Demostración:
(1) Como f y g son acotadas, también f + g es acotada.
Sea P una partición cualquiera de A, y R ∈ RP un rectángulo cualquiera definido por P .
entonces
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
mR (f + g) = inf{f (x) + g(x), x ∈ R} ≥
≥ inf{f (x), x ∈ R} + inf{g(y), y ∈ R} = mR (f ) + mR (g)
y
MR (f + g) = sup{f (x) + g(x), x ∈ R} ≤
≤ sup{f (x), x ∈ R} + sup{g(y), y ∈ R} = MR (f ) + MR (g)
En consecuencia, multiplicando por v(R) y sumando
Z
S(f, P ) + S(g, P ) ≤ S(f + g, P ) ≤
(f + g)
JJ
II
J
I
A
Z
≤ ≤
(f + g) ≤ S(f + g, P ) ≤ S(f, P ) + S(g, P )
A
Si tomamos ahora dos particiones cualesquiera de A, P 1 y P 2 , y consideramos la unión
P = P 1 ∪ P 2 , tenemos
S(f, P 1 ) + S(g, P 2 ) ≤ S(f, P ) + S(g, P ) ≤ S(f + g, P )
Z
Z
≤
(f + g) ≤
(f + g) ≤ S(f + g, P ) ≤
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
A
A
≤ S(f, P ) + S(g, P ) ≤ S(f, P 1 ) + S(g, P 2 )
Dejando fija P 2 , y tomando a la izquierda de la cadena supremos en P 1 , como f es integrable
queda
Z
Z
Z
2
f + S(g, P ) ≤
(f + g) ≤
(f + g) ≤ S(f, P 1 ) + S(g, P 2 )
A
A
A
y tomando ahora supremos en P 2
Z
Z
Z
Z
f+
g≤
(f + g) ≤
A
JJ
II
J
I
A
A
(f + g) ≤ S(f, P 1 ) + S(g, P 2 )
A
Repitiendo estos argumentos con la parte derecha de la desigualdad, tomando ı́nfimos en vez
de supremos, obtenemos
Z
Z
Z
Z
Z
Z
f+
g≤
(f + g) ≤
(f + g) ≤
f+
g
A
A
A
A
A
A
luego en efecto f + g es integrable, y su integral es la suma de las integrales de f y g
(2) Si f es integrable, entonces es acotada y evidentemente entonces también αf es acotada.
Supongamos ahora que α ≥ 0.
Sea P una partición cualquiera de A, y R uno de los rectángulos de RP .
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
mR (αf ) = inf{αf (x), x ∈ R} = α inf{f (x), x ∈ R} = αmR (f )
y análogamente
MR (αf ) = sup{αf (x), x ∈ R} = α sup{f (x), x ∈ R} = αMR (f )
Entonces, multiplicando por el volumen de cada rectángulo de la partición, y sumando
X
X
mR (αf )v(R) =
αmR (f )v(R) = αS(f, P )
S(αf, P ) =
R∈RP
JJ
II
J
I
r∈RP
y
S(αf, P ) =
X
R∈RP
MR (αf )v(R) =
X
r∈RP
αMR (f )v(R) = αS(f, P )
Por tanto
Z
αf = sup{S(αf, P ), P partición de A} =
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
= sup{αS(f, P ), P partición de A} =
= α sup{S(f, P ), P partición de A} =
Z
f
= α
A
y análogamente
Z
αf = inf{S(αf, P ), P partición de A} =
A
= inf{αS(f, P ), P partición de A} =
= α inf{S(f, P ), P partición de A} =
Z
= α
f
JJ
II
J
I
A
R
R
Ası́ que como f es integrable, αf también lo es, y A αf = α A f
Cuando α < 0, hay que tener en cuenta que para sacar α de un supremo o un ı́nfimo, hay
que cambiar el sentido de las desigualdades, con lo que se cambian los ı́nfimos por supremos y
los supremos por ı́nfimos:
mR (αf ) = inf{αf (x), x ∈ R} = α sup{f (x), x ∈ R} = αMR (f )
y análogamente
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
MR (αf ) = sup{αf (x), x ∈ R} = α inf{f (x), x ∈ R} = αmR (f )
de modo que
S(αf, P ) =
X
mR (αf )v(R) =
R∈RP
X
αMR (f )v(R) = αS(f, P )
r∈RP
y
S(αf, P ) =
X
MR (αf )v(R) =
R∈RP
X
αmR (f )v(R) = αS(f, P )
r∈RP
De aquı́
Z
αf = sup{S(αf, P ), P partición de A} =
JJ
II
J
I
A
= sup{αS(f, P ), P partición de A} =
= α inf{S(f, P ), P partición de A} =
Z
= α
f
A
y análogamente
Z
αf = inf{S(αf, P ), P partición de A} =
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
= inf{αS(f, P ), P partición de A} =
= α sup{S(f, P ), P partición de A} =
Z
= α
f
A
Ası́ que también αf es integrable y
R
A
αf = α
R
A
f
(3) Es trivial, ya que si f (x) ≥ 0 para todo x ∈ A, entonces
Z
Z
f≥
f ≥ mA (f )v(A) ≥ 0
A
JJ
II
J
I
A
R
(4)
Se
deduce
de
las
tres
propiedades
anteriores:
por
(2),
−g
es
integrable,
y
R
R
R
R
R A (−g)
R =
− A g. Por (1), f − g = f + (−g) es integrable, y A (f − g) = A f + A (−g) = A f − A g.
Y por (3), como f (x) − g(x) ≥ 0 para todo x ∈ A,
Z
Z
Z
f−
g = (f − g) ≥ 0
A
A
A
luego
Z
Z
f≥
A
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
g
A
(5) Como f es integrable, en particular es acotada, y por tanto también |f | es acotada.
Sea P una partición cualquiera de A, y R uno de los rectángulos definidos por P , R ∈ RP ,
y sean x e y dos puntos cualesquiera en R. Se tiene
mR (f ) − MR (f ) ≤ f (x) − f (y) ≤ MR (f ) − mR (f )
luego
|f (x)| − |f (y)| ≤ | |f (x)| − |f (y)| | ≤ |f (x) − f (y)| ≤ MR (f ) − mR (f )
y tomando supremos en x e ı́nfimos en y,
MR (|f |) − mR (|f |) ≤ MR (f ) − mR (f )
Multiplicando cada una de estas desigualdades por el volumen de R, y sumando
JJ
II
J
I
S(|f |, P ) − S(|f |, P ) =
X
(MR (|f |) − mR (|f |)) v(R) ≤
R∈RP
≤
X
R∈RP
(MR (f ) − mR (f )) v(R) ≤ S(f, P ) − S(f, P )
Como f es integrable, aplicando el Criterio de Riemann, dado > 0 existe alguna partición
P de A tal que S(f, P ) − S(f, P ) < . Y entonces
S(|f |, P ) − S(|f |, P ) ≤ S(f, P ) − S(f, P ) < Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
luego aplicando el mismo criterio a |f |, también es integrable.
Además, como para todo x ∈ A
−|f (x)| ≤ f (x) ≤ |f (x)|
aplicando las propiedades (2) y (4)
Z
Z
Z
− |f | ≤
f≤
|f |
A
JJ
II
J
I
de donde
Z
A
A
A
se deduce que
Z
f ≤
|f |
A
(6) Basta observar que para cada cada x ∈ A
max{f, g}(x) = max{f (x), g(x)} =
f (x) + g(x) + |f (x) − g(x)|
2
y
min{f, g}(x) = min{f (x), g(x)} =
f (x) + g(x) − |f (x) − g(x)|
2
y aplicar las propiedades anteriores.
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
(7) Como f es integrable, es acotada, y entonces también f 2 es acotada. Además también
|f | es integrable, como ya hemos visto.
Sea k > 0 tal que |f (x)| ≤ k para todo x ∈ A, y sea > 0. Aplicando el criterio de Riemann
a la función |f |, existe una partición P de A tal que
S(|f |, P ) − S(|f |, P ) ≤
2k
Si R es uno de los rectángulos definidos por esa partición, tenemos
JJ
II
J
I
MR (f 2 ) = sup{f 2 (x), x ∈ R} = sup{|f (x)|2 , x ∈ R} =
= sup{|f (x)|, x ∈ R}2 = MR (|f |)2
mR (f 2 ) = inf{f 2 (x), x ∈ R} = inf{|f (x)|2 , x ∈ R} =
= inf{|f (x)|, x ∈ R}2 = mR (|f |)2
(es decir, el cuadrado se puede sacar fuera del supremo y del ı́nfimo de una familia de números
positivos)
Entonces
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
MR (f 2 ) − mR (f 2 ) = MR (|f |)2 − mR (|f |)2 =
= (MR (|f |) − mR (|f |))(MR (|f |) + mR (|f |))
≤ 2k(MR (|f |) − mR (|f |))
Multiplicando estas desigualdades por el volumen de cada rectángulo R, y sumando, queda
S(f 2 , P ) − S(f 2 , P ) ≤ 2k(S(|f |, P ) − S(|f |, P )) ≤ 2k
=
2k
Aplicando el criterio de Riemann a la función f 2 , ésta es integrable.
(8) Por último, para demostrar que el producto de f y g es integrable basta escribir
JJ
II
J
I
fg =
(f + g)2 − (f − g)2
4
y aplicar las propiedades anteriores.
J(Volver al enunciado)
Y además
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
Proposición.
Sea P una partición cualquiera de A. f es integrable en A si y sólo si para cada rectángulo
R ∈ RP la restricción de f a R es integrable. Además en este caso
Z
X Z
f=
f
A
R∈RP
R
Demostración:
Sea P una partición cualquiera de A.
Supongamos primero que f es integrable en A,
Aplicando el criterio de Riemann a A, dado > 0 existe una partición P de A tal que
S(f, P )−S(f, P ) < . Consideramos entonces en A la unión de las dos particiones, Q = P ∪P ,
que es mayor que P , con lo que
S(f, Q) − S(f, Q) ≤ S(f, P ) − S(f, P ) < JJ
II
J
I
y también es mayor que P , con lo que define sobre cada rectángulo R ∈ RP una partición QR .
Los rectángulos definidos por QR en R son los rectángulos S ∈ RQ que están contenidos en R.
P
P
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
R
Q = P ∪ P
S
R
Para un rectángulo R ∈ RP cualquiera, si calculamos para esa partición QR definida en R la
diferencia entre la suma superior y la inferior, obtendremos
JJ
II
J
I
S(f |R , QR ) − S(f |R , QR ) =
X
[MS (f ) − mS (f )]v(S) ≤
S∈RQ ,S⊆R
≤
X
[MS (f ) − mS (f )]v(S) =
S∈RQ
= S(f, Q) − S(f, Q) < Por tanto la restricción de f a R es integrable.
Recı́procamente, supongamos que la restricción de f a cada rectángulo R de RP es integrable.
Dado > 0, aplicando en cada rectángulo R el criterio de Riemann, existirá una partición PR
de R tal que
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
S(f |R , PR ) − S(f |R , PR ) ≤
k
donde k es el número de rectángulos definidos por la partición P .
Definimos entonces la partición Q de A unión de la partición original P y todas las particiones
PR , que es mayor que P , y define en cada rectángulo R de RP una partición QR mayor que PR ,
formada por los rectángulos S ∈ RQ que están contenidos en R
PR1
R1
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
PR2
R2
P
P
QR1
QR2
Q = P ∪ PR1 ∪ PR2
JJ
II
J
I
Para calcular la diferencia entre la sumas superior e inferior definidas por Q, aplicamos
la propiedad distributiva de la suma, agrupando los rectángulos S ∈ RQ que están en cada
rectángulo R ∈ RP
S(f, Q) − S(f, Q) =
X
[MS (f ) − mS (f )]v(S) =
S∈RQ
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
=
X
X
R∈RP
[MS (f ) − mS (f )]v(S) =
S∈RQ ,S⊆R
=
X
X
R∈RP
=
[MS (f ) − mS (f )]v(S) =
S∈RQR
X S(f |R , QR ) − S(f |R , QR ) ≤
R∈RP
≤
X S(f |R , PR ) − S(f |R , PR ) ≤
R∈RP
≤
JJ
II
J
I
X =
k
R∈R
P
Por tanto f es integrable en A.
Además, si P 0 es ahora una partición cualquiera de A, y consideramos la unión Q = P ∪ P 0 ,
y como antes la partición QR definida por Q en cada rectángulo R de RP , tenemos
S(f, P 0 ) ≤ S(f, Q) =
X
mS (f )v(S) =
S∈RQ
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
=
X
R∈RP
=
X
X
R∈RP
mS (f )v(S) =
S∈RQ ,S⊆R
S(f |R , QR ) ≤
X Z
R∈RP
f
R
y tomando supremos cuando P 0 recorre todas las posibles particiones de A se tiene
Z
X Z
f≤
f
A
R∈RP
Análogamente
JJ
II
J
I
R
S(f, P 0 ) ≤ S(f, Q) =
X
MS (f )v(S) =
S∈RQ
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
X
=
X
R∈RP
X
=
R∈RP
MS (f )v(S) =
S∈RQ ,S⊆R
S(f |R , QR ) ≥
X Z
R∈RP
f
R
y tomando ı́nfimos cuando P 0 recorre todas las posibles particiones de A, se tiene
Z
f≥
A
JJ
II
J
I
X Z
R∈RP
f
R
Por tanto
Z
X Z
f=
f
A
R∈RP
R
Ejemplo 4. Las funciones f + y f −
Un caso particular que se deduce de las propiedades anteriores, y que jugará un papel especial
en la teorı́a de integración es el de las funciones f + y f − .
Dada una función f : A −→ R, se llaman
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
JJ
II
J
I
f + (x) = max{f (x), 0}
y
f − (x) = − min{f (x), 0} = max{−f (x), 0}
f
Integral de
Riemann en Rn .
Concepto y
Propiedades
Fundamentales.
f+
f−
Contenido
Las funciones f + y f − son funciones no negativas, y cumplen
f = f+ − f−
JJ
II
J
I
y
|f | = f + + f −
de donde se deduce, por ejemplo, que f es integrable si y sólo si f + y f − son integrables.