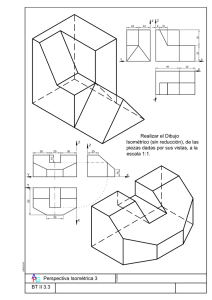
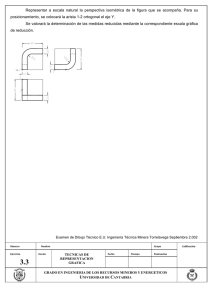
SISTEMAS DE REPRESENTACIN

©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
SISTEMAS DE REPRESENTACIÓN. No es habitual, que la persona que diseña un objeto sea luego la misma que se encarga de
su construcción. Por ello, la información gráfica tiene que ser accesible a todas las personas que
quieran contemplarlo o bien construirlo.
Los procedimientos que se emplean para la difusión gráfica de ideas y diseños son los
sistemas de representación. Todos estos sistemas se basan en la representación de los objetos
por medio del empleo de las proyecciones.
PROYECCIONES Si interponemos una cartulina cuadrada entre el haz de luz que produce un foco y la superficie
de una mesa, se produce una sombra que va cambiando de tamaño a medida que la cartulina se
acerca o se aleja de la mesa. Lo mismo sucede si es el foco de luz el que se acerca o se aleja.
Esta sombra, que no es más que la proyección cónica de la cartulina, no da la visión real de la
cartulina, sino una imagen deformada del diseño real.
Uno de los sistemas de representación que más se emplean, el llamado sistema cónico o
central, se basa en las proyecciones cónicas, ya que la sensaciones de profundidad que se
consiguen por este método son similares a las que se obtienen cuando se ven los objetos tal y
como son en la realidad.
Persepectiva isométrica
-1-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Si en vez de un foco de luz tuviésemos una fuente de luz de un enorme tamaño, o bien
situáramos el foco en el infinito, los rayos de luz serían prácticamente paralelos, y, por lo tanto,
la imagen real de la cartulina no sufriría ningún tipo de deformación, manteniendo la sombra el
mismo tamaño que el original. En este caso, la proyección o sombra obtenida de la cartulina
cuadrada sería una proyección cilíndrica. Si el plano de la mesa es perpendicular a los rayos de
la luz, se dice que la proyección cilíndrica es ortogonal; en caso contrario, la proyección es
oblicua.
Hay tres sistemas de representación en los que se utilizan las proyecciones cilíndricas; a
saber: el sistema diédrico, el sistema acotado y el sistema axonométrico.
Persepectiva isométrica
-2-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
PERSPECTIVA ISOMÉTRICA. La forma más fácil y lógica de situar los objetos para su representación gráfica es hacer
que sus ejes tridimensionales queden paralelos a los del sistema de coordenadas, es decir que las
direcciones principales del objeto que se va a representar coincidan con las direcciones de los
ejes. La proyección de los objetos que se obtiene por este procedimiento se llama perspectiva
isométrica.
La perspectiva isométrica pertenece al sistema axonométrico de representación y se emplea
para representar los objetos mediante proyecciones cilíndricas ortogonales sobre un plano, que es
el papel. Para ello utiliza un sistema de ejes de coordenadas constituido por tres ejes que forman
entre sí ángulos de 120º.
Persepectiva isométrica
-3-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Los ejes de coordenadas se denominan X, Y y Z, se cortan en el origen 0 y forman, dos a
dos, tres planos de referencia o de coordenadas que se denominan de la siguiente manera: al
plano XY se le llama horizontal; al XZ, vertical o vertical primero, y al YZ, de perfil o vertical
segundo. Sobre el eje X se mide la longitud; sobre el Y, la anchura, y en el Z se sitúa la altura.
El procedimiento para representar un punto en el sistema isométrico recuerda mucho a la
manera de representar un punto del plano en sus ejes de coordenadas. La clave está en llevar las
coordenadas del punto a los ejes y trazar desde allí paralelas a los otros ejes. En el punto en el
que se cortan las líneas paralelas, allí está nuestro punto.
En el ejemplo del dibujo se representa el punto P (3, 5, 2). Se lleva sobre el eje OX el valor 3,
y sobre el eje OY, el valor 5. Se traza por el punto marcado en el eje OX una línea paralela al eje
OY, y, viceversa, por el punto marcado en OY una paralela a OX. Las dos líneas se cortan en un
punto por el que se traza una paralela al tercer eje. Al llevar sobre esta línea la tercera
coordenada, es decir, el 2, habremos conseguido representar el punto. Para representar un
segmento, es suficiente con representar sus dos puntos extremos y unirlos a continuación.
Persepectiva isométrica
-4-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Para trazar figuras planas sobre cualquiera de los planos de coordenadas o de referencia,
basta llevar sobre los ejes correspondientes de cada plano las medidas que tiene la figura,
trazando a continuación líneas paralelas al otro eje del plano hasta que se corten. Cuando las
figuras planas son algo complicadas, será necesario ayudarse de líneas auxiliares.
Persepectiva isométrica
-5-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
A la hora de representar objetos sólidos sencillos limitados por caras planas, lo primero que
hay que hacer es situarlos de manera que sus ejes fundamentales sean paralelos a los de los ejes
de coordenadas. A continuación, se traza, si es posible, la planta del cuerpo, y se levantan líneas
paralelas por los diferentes vértices al eje OZ, sobre las que se lleva la altura del cuerpo.
También se puede dibujar el perfil de la figura y trazar líneas paralelas a los ejes X o Y,
dependiendo de si dicho perfil se ha dibujado en el plano YZ o en el XZ. Sobre esas líneas se
llevarían la longitud o la anchura del cuerpo.
Persepectiva isométrica
-6-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Los círculos en la perspectiva isométrica se transforman en elipses, pero al resultar un tanto
complicado trazarlas, se sustituyen por óvalos, que son más fáciles de representar y suponen una
buena aproximación del círculo. Estos óvalos se forman con cuatro arcos de circunferencia, que
se trazan fácilmente con el compás.
Para calcular los puntos sobre los que pincharemos el compás, hay que dibujar previamente
un cuadrado cuyo lado sea igual al diámetro del círculo y trazar en él a continuación las
diagonales, cuyo punto de corte será el centro, tanto del cuadrado como del círculo. Por el
centro así obtenido se trazan líneas paralelas a los lados del cuadrado, cortando a este en cuatro
puntos: A, B, C y D.
Los extremos de la diagonal más corta son los dos primeros centros que buscamos. Los otros
dos serán los puntos de corte de las líneas, que, partiendo de los extremos de dicha diagonal, van
a parar a los puntos A, B, C y D. Con centro en los puntos 1, 2, 3 y 4 y radios respectivos los
segmentos 1C, 2D, 3A y 4B, se trazan los cuatro arcos de circunferencia.
Persepectiva isométrica
-7-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Persepectiva isométrica
-8-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Persepectiva isométrica
-9-
©NGHG
Departamento de Tecnología
I.E.S. San José (Villanueva de la Serena)
2º ESO
Bloque de contenidos: EXPRESIÓN GRÁFICA
Actividades.
1. Dibujar la perspectiva isométrica de la siguiente figura dada por sus vistas.
Persepectiva isométrica
- 10 -