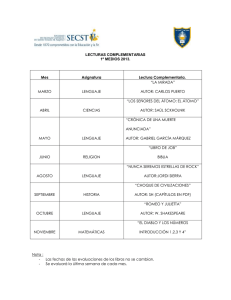
ˆ ˆˆ H HH = )(ψ)(ψ),( r r rr о о оо = Ψ )(ψ )(ψˆ )(ψ )(ψˆ r E r H r E r H о
Anuncio

CAPITULO 4. El átomo de hidrógeno 1) Atomo de hidrógeno e hidrogenoides Z = número atómico o número de protones del núcleo + Z = 1 (H); 2 (He ); 3 (Li2+). z e F F e e θ = = = = q1 q2/4 π ε0 r2 q1 q2 / r2 1.6021 10-19 cul 4.8030 10-10 uee r N x euee = ecul/(4 π ε0 )1/2 y φ V(r)= -Ze2/r (euee) r r r r Ψ (re , rN ) = ψCM (rCM )ψint (r ) Hˆ = Hˆ CM + Hˆ int r r Hˆ CM ψCM (rCM ) = ECM ψ CM (rCM ) r r Hˆ int ψ int (r ) = Eint ψint (r ) µ= mn ⋅ me mn + me Ĥ = - h2 2 Z e2 ∇ 2µ r [4.1] En un sistema de fuerzas centrales, las funciones propias de Ĥ son del tipo R(r).Y(θ,φ). Para encontrar R(r) se resuelve la ecuación diferencial [3.25]. h2 2 1 Z e2 2 l (l + 1) h R(r) R(r) = E R(r) R'' (r) + R' (r ) + 2 2µ r r 2µr Transformando esta ecuación y haciendo R'' (r) + a= [4.2] h2 µ e2 2 2 E 2 Z l (l + 1) R' (r) + 2 + R(r) = 0 r ar r2 ae [4.3] Cuando r→∞, (1/r)→0, [4.2] se transforma en: R'' (r) + 2E R(r) = 0 a e2 Ecuación análoga a [2.2] cuya solución era del tipo [2.3] Cap.4. El átomo de hidrógeno 1 2E E ≥ 0, - 2 ae 1/2 2E =i 2 ae 1/2 (número imaginario) 2 1/2 R(r) = k e ± (2E/ae ) r = k e ± i r 2Eµ /h [4.4] Son las funciones propias del continuo. El núcleo y el electrón están tan lejos que V(r) = 0 y el electrón se comporta como una partícula libre. 2E Si E < 0, - 2 ae 1/2 (número real y positivo). Son los estados enlazantes. R(r) = K(r) e - r - 2 E/a e 2 [4.5] Sustituyendo [4.5] en [4.3] se obtiene la ecuación diferencial: γ l (l + 1) 2 ε 2 K =0 K'' + - ε K' + 2 r r r r γ= 2 Z µ e2 h2 Haciendo: r = K'' = ρ 2 ε ; n= ∂ 2 K (r ) ∂r 2 γ ; 2 ε ε=- 2E 2Eµ =- 2 2 ae h K' = ∂ K (r ) ∂r K(r) = ρ l L(ρ) L' ' + (2(l + 1) - ρ ) L' + (n - (l + 1) ) L = 0 [4.6] que es la ecuación asociada de Laguerre, cuyas soluciones son aceptables siempre que n sea un número entero y positivo y n(l+1) no sea negativo. Por tanto para los átomos; l = 0, 1, … (n-1) La energía está cuantizada Z2 e2 µ Z 2 e4 E==2 a n2 2 h2 n2 ( n = 1, 2, 3, …) E Contínuo, N y e no interaccionan 0 n=4 n=3 V=-Ze’ 2 /r Los niveles de energía están n2 veces degenerados. Las soluciones de [4.6] son los polinomios asociados de Laguerre que dependen de n y l; n=2 n=1 Cap.4. El átomo de hidrógeno [4.7] 2 R n ,l (r ) = ρ l L n,l (ρ) e - ρ/2 ρ= 2 Z r 2 Z µ e2 r = an n h2 [8.9] h2 ; µ e2 a= a0 = h2 =0.5929 Å (radio de Bohr) me e2 (µH = 0.9946 me) 2) Funciones radiales de los átomos hidrogenoides 1s, Z R 1,0 = 2 a 1 = 2 3/2 Z a e -Zr/a 3/2 Z r -Zr/2a 1 e 2a 2s, R 2,0 5/2 2p, 1 Z R 2,1 = 2 6a 3/2 3s, R 3,0 2 Z = 3 3a 3p, R 3,1 = 3d, R 3,2 r e -Zr/2a 8 Z 27 6 a 3/2 Z = 81 30 a 4 2 Z r 2 Z 2 r 2 -Zr/3a 1 e + 3a 27 a 2 Z r Z 2 r 2 -Zr/3a e − 6 a 2 a 7/2 r 2 e -Zr/3a El factor rl hace que Rn.l sea nulo en el origen, excepto para Rn,0 (ns). Si l = 0 el momento angular es nulo. 1s 2s 3s 2p 3p r/a Cap.4. El átomo de hidrógeno 3 3d E=− µZ 2euee 4 1 2h 2 µ Z 2 ec 4 1 =− n2 32π 2ε 02h 2 n 2 4 1 E 2 − E1 µZ 2euee 2π 2 1 1 1 − = RZ 2 − υ = = = n2 n2 n2 n2 c hc h3c 1 1 2 2 υ (Mod. Atómico de Bohr) 1 1 − ni2 n 2j ν = RH ( RH = cte de Rydberg) 2π 2 µe 4 R= h3c µ= Mm M +m 2π 2 me e 4 = 109737.3 cm -1 R∞ = 3 hc ⇒ 2π 2 µe 4 = 109677.6 cm -1 RH = 3 hc µH = m p me m p + me = 0.9994557 me ; µ ∞ = me mp=1836 me Cap.4. El átomo de hidrógeno 4 3) Orbitales hidrogenoides. Función de onda de un electrón Ψn,l,m(r,θ,φ) = Rn,l(r).Yl,m(θ,φ) es un orbital. Valor de l nombre del orbital 0 s 1 p 2 d 3 f 4 g Probabilidad infinitesimal de encontrar al electrón elemento diferencial de volumen, dτ = r2 senθ dr dθ dφ. 2 en un 2 2 Ψn ,l ,m (r , θ, φ) r 2 senθ dr dθ dφ = R n,l (r ) Ylm (θ, φ) r 2 senθ dr dθ dφ Probabilidad de encontrar al electrón en una delgada superficie esférica de radio comprendido entre r y r+dr. π 2π ∫ ∫ R(r) 2 2 Y(θ, φ ) r 2 sen θ dr dθ dφ = R 2 r 2 dr 0 0 Función de distribución radial : R2 r2. ( d R n2 ,l r 2 dr )=0 (radio más probable) R2 r 2 rm 2s <r> 2p 1s r/a r/a Un orbital Ψn,l,m(r,θ,φ) tiene imaginaria la parte en φ. Para trabajar con funciones reales se hacen combinaciones lineales de las funciones con valores -m y +m. Las funciones resultantes son orbitales reales, son funciones propias de Ĥ y L̂2 pero no de L̂ z . 1 1 Z 2p x = (2p1 + 2p -1 ) = 2 4 2π a Cap.4. El átomo de hidrógeno 5 5/2 e -Zr/2a r senθ cosφ como x = r senθ cosφ, la máxima probabilidad de encontrar al electrón en este estado es a lo largo del eje x. Se denomina orbital 2px. 1 1 Z 2p y = (2p1 − 2p -1 ) = i 2 4 2π a 3d x 2 - y2 5/2 e -Zr/2a r senθ senφ 1 (3d 2 + 3d −2 ) = 1 Z = 2 81 2π a 7/2 e -Zr/3a r 2 sen 2 θ cos2φ Funciones de onda hidrogenoides (orbitales) reales: 1s = 1 Z π a Z 2p z = 4 2π a 1 3/2 e - Zr/a 2s = 5/2 e - Zr/2a Z 2p y = 4 2π a 1 Z 4 2π a 1 Z 2p x = 4 2π a 1 r cosθ 5/2 e - Zr/2a r senθ senφ 3/2 Zr Z 2r 2 27 - 18 + 2 2 a a 2 Z 3p z = 81 π a 5/2 Zr - Zr/3a r cosθ 6 - e a 2 Z 81 π a 5/2 Zr - Zr/3a r senθ cosφ 6 - e a 2 Z 3p y = 81 π a 5/2 Zr - Zr/3a r senθ senφ 6 - e a 3s = Z 81 3π a 1 3p x = 3d z 2 Z = 81 6π a 1 7/2 2 Z 81 π a 7/2 2 Z 3d yz = 81 π a 7/2 3d xz = Cap.4. El átomo de hidrógeno 3/2 ( - Zr/3a e ) e - Zr/3a r 2 3 cos 2θ - 1 e - Zr/3a r 2 senθ cosθ cosφ e - Zr/3a r 2 senθ cosθ senφ 6 Zr - Zr/2a 2 - e a 5/2 e - Zr/2a r senθ cosφ 7/2 3d xy = Z 81 2π a 3d x 2 - y 2 Z = 81 2π a 1 1 e - Zr/3a r 2 sen 2θ sen2φ 7/2 e - Zr/3a r 2 sen 2θ cos2φ Representación gráfica de los orbitales hidrogenoides Método I. Dibujar las gráficas de las funciones a) Representación de R(r) b) Representación de la parte angular de Ψ Método II. Dibujar los contornos de densidad de probabilidad cte (2D-3D) 95% p s p s 50% 3dxy , 3dyz , 3dxz , 3dx2-y 2 3dz2 Ejemplo 4.1. Calcule el radio más probable para el orbital 1s. Solución: Z R 1,0 = 2 a 1s, ( 3/2 3 Z R n,2 l r 2 = 4 e -2Zr/a r 2 a e -Zr/a ) d R 2r 2 2Z 2 − 2 Zr / a Zr = N r e + 2 r e -2Zr/a = 2 r N e -2Zr/a + 1 = 0 dr a a rmin = 0 rmin = ∞ rmax = a/Z Para el átomo de hidrógeno: Z=1, µ=me Cap.4. El átomo de hidrógeno rmax = a0 7 Ejemplo 4.2. Calcula el radio medio del orbital 1s. Solución: según el tercer postulado (ecuación [1.10]) < r >= ∫ Ψ * r̂ Ψ dτ 1Z <r>= π a 3 <r>= <r>=∫ 3 ∫e 1 π - 2Zr/a Z a 3/2 1 Z r r sen θ dr dθ dφ = πa e - Zr/a 3∞ 2 ∫e 3/2 e -Zr/a dτ π 2π 0 0 r dr ∫ senθ dθ ∫ dφ - 2Zr/a 3 0 1 Z 3a Z 3 21 - 2Zr/a 3 r dr = 4 = 4 π∫ e 4 πa 2Z a (2Z/a) 0 1 l(l + 1) a < r > n,l,m = n 2 l + 1 − n 2 Z 2 ( ∫ e −ax x n dx = 0 Z a 3 ∞ En general: ∞ 1 r π [8.10] n! ) a n +1 4) Espín del electrón En mecánica cuántica no relativista, el espín de las partículas se introduce como un postulado más. El momento angular de espín es propio de cada partícula. Es un momento angular intrínseco y no se asemeja a ninguna magnitud en mecánica clásica. Los operadores relacionados con él funcionan de manera análoga a los del momento angular orbital L̂ . Ŝ 2 , Ŝ x , Ŝ y , Ŝ z [Ŝ , Ŝ ]= i h Ŝ x y Cap.4. El átomo de hidrógeno z [4.12] Ŝ 2 = Ŝ 2x + Ŝ 2y + Ŝ 2z [4.11] [Ŝ , Ŝ ]= i h Ŝ [4.13] y 8 z x [Ŝ , Ŝ ]= i h Ŝ z x [4.14] y [Ŝ , Ŝ ] = [Ŝ , Ŝ ] = [Ŝ , Ŝ ] = 0 2 x 2 y 2 z Aunque no se conozcan las funciones propias, pueden conocerse los valores propios de Ŝ 2 y Ŝ z mediante los operadores de escalonamiento (ascendente y descendente). Ŝ 2 f = s (s + 1) h 2 f s = número cuántico de espín = 0, 1/2, 1, 3/2, 2, . Ŝ z f = m s h f ms = número cuántico = -s, -(s+1),-(s+1),... +s. Electrones, protones, neutrones: s = 1/2 ms = + 1/2, -1/2 Las funciones α y β son las funciones propias de los operadores Ŝ 2 y Ŝ z . Ŝ 2 α = 1/2 (1 + 1/2) h 2 α ; Ŝ 2 β = 1/2 (1 + 1/2) h 2 β [4.15] Ŝ z α = 1/2 h α Ŝ z β = - 1/2 h β [4.16] Estado 1/ 2 h α 3/2h Estado β 3/2h − 1/ 2 h Se toma como coordenada de espín ms. Puesto que α y β deben ser ortonormales: 1/ 2 2 ∑ [α(m s )] = 1 1/ 2 2 ∑ [β(m s )] = 1 ∑ α * (m ) β(m ) = 0 −1 / 2 −1 / 2 −1 / 2 Cap.4. El átomo de hidrógeno 9 1/ 2 s s Se toma: α(1/2) = 1 ; β(1/2) = 0 ; α(-1/2) = 0 β(-1/2) = 1 [4.17] [4.18] La función de onda total que describe a un electrón es el producto de la función espacial y la función de espín Ψ(x,y,z) α ó Ψ(x,y,z) β En el átomo de hidrógeno, la función total depende de cuatro números cuánticos: n, l, m (ml) y ms. 5) El momento magnético del electrón en el átomo de hidrógeno El desdoblamiento de cada línea es de 0.016 nm, lo que equivale a una diferencia de energía de 0.000045 eV Según el electromagnetismo clásico, el momento magnético asociado a una carga q que se mueve a velocidad v en una espira de radio r y por tanto con momento angular orbital L es igual a: r µL = q r L 2mc (q = - e, para el electrón) El operador asociado es: µˆ L = − e L̂ 2 me c [4.19] r Ya que los valores de L son conocidos, se obtiene: Cap.4. El átomo de hidrógeno 10 µL = e h l(l + 1) 2 me c µB = e h = 9.27 10 -21 erg/gauss 2 me c [4.20] (magnetón de Bohr) El electrón tiene en el átomo un momento magnético debido al momento angular orbital dado por [4.19] y [4.20] Debido al momento angular de espín, momento magnético de espín intrínseco r µS = − ge e r S 2 me c el electrón tiene un [4.21] (g e ≈ 2) r r Los dos campos magnéticos generados por L y S interaccionan y los vectores del momento angular orbital y de espín se acoplan r dando lugar al momento angular total J . r El nuevo vector J , tiene asociado el número cuántico j. Ĵ 2 Ψ (r, θ, φ, m s ) = j (j + 1) h 2 Ψ (r, θ, φ, m s ) [4.22] Ĵ z Ψ (r, θ, φ, m s ) = m j h Ψ (r, θ, φ, m s ) [4.23] j = (l+s), (l+s-1), (l+s-2), .... +|l-s| mj = -j, -j+1, -j+2, .... +j. Si no se tiene en cuenta el espín, la energía sólo depende del número cuántico n [8.7]. Al considerar la energía de interacción entre los dos momentos magnéticos, la energía depende de n y j. E n, j = - R c α2 Z2 1 3 1+ − 2 n j + 1 / 2 4 n n E n, j = - Z 2 µ e4 2 n2 h2 α2 Z2 1 + n 1 3 − j + 1 / 2 4 n R= Z 2 µ e4 2 c h2 (constante de Rydberg) α= e2 hc (constante de estructura fina) Cap.4. El átomo de hidrógeno 11 [4.24] Ejemplo 4.3. Determine el desdoblamiento en el espectro del átomo de H para la transición 3s-2p. Rc E n, j = - 2 n α2 Z2 1 + n 1 3 − j + 1 / 2 4 n α2 1 3 1 + − n j + 1 / 2 4 n RH c Para el H: E = n2 ( ) 2 e2 4,803207.1 0 -10 uee −3 α= = 7 , 2973 . 10 = hc 1,0546 .10 − 27 erg .s 299792 .10 5 cm / s ( ) α 2 = 5 , 3251 .10 − 5 α2 RH c 1 3 E 3s 1/2 = - 2 1 + − 3 1 / 2 + 1 / 2 4 .3 3 5,3251.10 - 5 1 RH c E 3s 1/2 = - 2 1 + 1 − = − 12186 ,56 c s -1 3 4 3 E 2p 1/2 RH c 1 3 α2 = - 2 1 + − 2 1 / 2 + 1 / 2 4 .2 2 E 2p 1/2 109677,581 c 5,3251.10 - 5 3 =1 + 1 − = − 27419 ,852 c s -1 2 2 8 2 Cap.4. El átomo de hidrógeno 12 E 2p 3/2 RH c 1 3 α2 1 + =− 2 3 / 2 + 1 / 2 4 .2 2 2 E 2p 3/2 = - 2 7419,487c E 3 s 1 / 2 - E 2p 3/2 = - 12186,560c + 27419,487c = 15232,927c s -1 λ 1 = 656 ,473 nm E 3 s 1 / 2 - E 2p 1/2 = − 12186,560c + 2 7419,852c = 15233 , 292 c s - 1 λ 2 = 656 ,457 nm λ 1 − λ 2 = 0 ,016 nm Cap.4. El átomo de hidrógeno 13 Cap.4. El átomo de hidrógeno 14