1 Agudeza visual. En un estudio sobre la agudeza visual se dispone
Anuncio
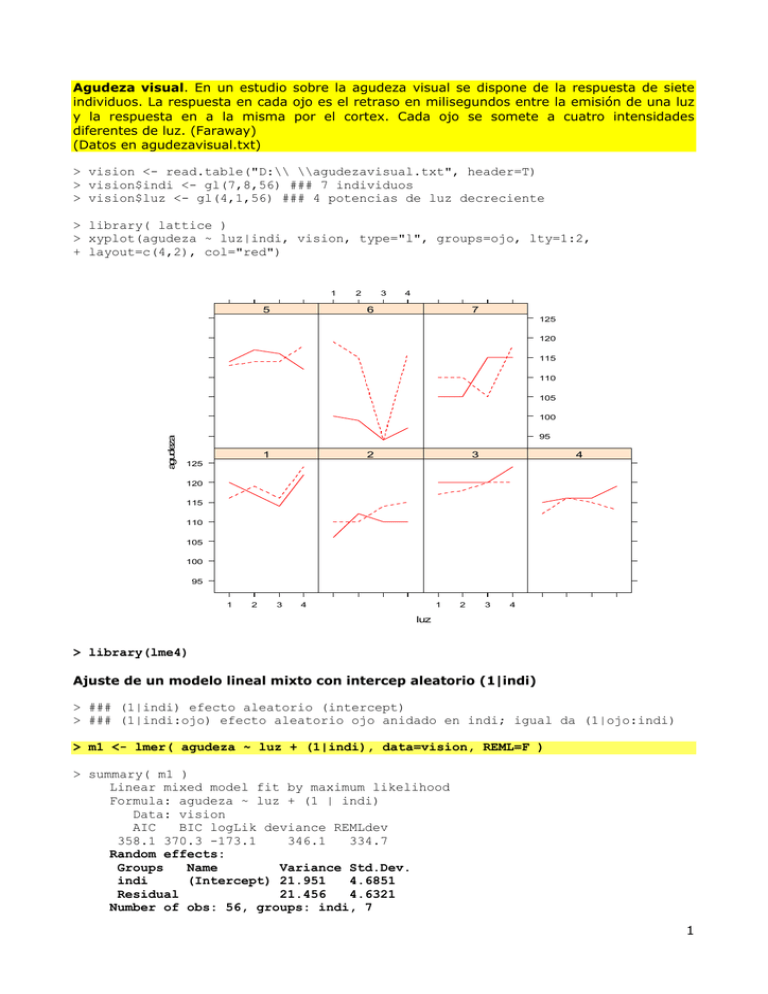
Agudeza visual. En un estudio sobre la agudeza visual se dispone de la respuesta de siete individuos. La respuesta en cada ojo es el retraso en milisegundos entre la emisión de una luz y la respuesta en a la misma por el cortex. Cada ojo se somete a cuatro intensidades diferentes de luz. (Faraway) (Datos en agudezavisual.txt) > vision <- read.table("D:\\ \\agudezavisual.txt", header=T) > vision$indi <- gl(7,8,56) ### 7 individuos > vision$luz <- gl(4,1,56) ### 4 potencias de luz decreciente > library( lattice ) > xyplot(agudeza ~ luz|indi, vision, type="l", groups=ojo, lty=1:2, + layout=c(4,2), col="red") 1 5 2 3 4 6 7 125 120 115 110 105 agudeza 100 95 1 2 3 4 125 120 115 110 105 100 95 1 2 3 4 1 2 3 4 luz > library(lme4) Ajuste de un modelo lineal mixto con intercep aleatorio (1|indi) > ### (1|indi) efecto aleatorio (intercept) > ### (1|indi:ojo) efecto aleatorio ojo anidado en indi; igual da (1|ojo:indi) > m1 <- lmer( agudeza ~ luz + (1|indi), data=vision, REML=F ) > summary( m1 ) Linear mixed model fit by maximum likelihood Formula: agudeza ~ luz + (1 | indi) Data: vision AIC BIC logLik deviance REMLdev 358.1 370.3 -173.1 346.1 334.7 Random effects: Groups Name Variance Std.Dev. indi (Intercept) 21.951 4.6851 Residual 21.456 4.6321 Number of obs: 56, groups: indi, 7 1 Fixed effects: Estimate Std. Error t value (Intercept) 112.6429 2.1605 52.14 luz2 0.7857 1.7508 0.45 luz3 -1.0000 1.7508 -0.57 luz4 3.2857 1.7508 1.88 Correlation of Fixed Effects: (Intr) luz2 luz3 luz2 -0.405 luz3 -0.405 0.500 luz4 -0.405 0.500 0.500 Añadimos el factor ojo anidado en el factor individuo: > m2 <- lmer( agudeza ~ luz + (1|indi) + (1|indi:ojo), data=vision, REML=F ) > summary( m2 ) Linear mixed model fit by maximum likelihood Formula: agudeza ~ luz + (1 | indi) + (1 | indi:ojo) Data: vision AIC BIC logLik deviance REMLdev 353.2 367.4 -169.6 339.2 328.7 Random effects: Groups Name Variance Std.Dev. indi:ojo (Intercept) 10.570 3.2512 indi (Intercept) 17.421 4.1738 Residual 15.416 3.9264 Number of obs: 56, groups: indi:ojo, 14; indi, 7 Fixed effects: Estimate Std. Error t value (Intercept) 112.6429 2.0843 54.04 luz2 0.7857 1.4840 0.53 luz3 -1.0000 1.4840 -0.67 luz4 3.2857 1.4840 2.21 Correlation of Fixed Effects: (Intr) luz2 luz3 luz2 -0.356 luz3 -0.356 0.500 luz4 -0.356 0.500 0.500 > anova( m2 ) Analysis of Variance Table Df Sum Sq Mean Sq F value luz 3 140.77 46.923 3.0437 Globalmente, el efecto fijo luz parece significativo. > anova( m1, m2 ) Data: vision Models: m1: agudeza ~ luz + (1 | indi) m2: agudeza ~ luz + (1 | indi) + (1 | indi:ojo) Df AIC BIC logLik Chisq Chi Df Pr(>Chisq) m1 6 358.14 370.29 -173.07 m2 7 353.18 367.36 -169.59 6.9608 1 0.008332 ** --Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1 2 > d.m1.m2 <- 2*(logLik(m2)-logLik(m1)) > pval.dev <- 1-pchisq( d.m1.m2, 1 ) > cbind( d.m1.m2, pval.dev ) d.m1.m2 pval.dev [1,] 6.96075 0.008331708 El modelo m2 es mejor que el modelo m1. El efecto luz3 es negativo: ¿ojo izquierdo del individuo 6 bajo luz=3? > m2.43 <- lmer( agudeza ~ luz + (1|indi) + (1|indi:ojo), + data=vision, subset=-43 ) > summary( m2.43 ) Linear mixed model fit by REML Formula: agudeza ~ luz + (1 | indi) + (1 | indi:ojo) Data: vision Subset: -43 AIC BIC logLik deviance REMLdev 312.9 326.9 -149.4 307.1 298.9 Random effects: Groups Name Variance Std.Dev. indi:ojo (Intercept) 24.7024 4.9702 indi (Intercept) 8.2614 2.8743 Residual 8.2733 2.8763 Number of obs: 55, groups: indi:ojo, 14; indi, 7 Fixed effects: Estimate Std. Error t value (Intercept) 112.6429 1.8803 59.91 luz2 0.7857 1.0871 0.72 luz3 0.5214 1.1141 0.47 luz4 3.2857 1.0871 3.02 0 -2 -4 residuals(m2.43) 2 > ### residuos de m2.43 > x11() > plot( fitted(m2.43), residuals( m2.43) ) > abline( h=0, lty=3 ) 4 Correlation of Fixed Effects: (Intr) luz2 luz3 luz2 -0.289 luz3 -0.282 0.488 luz4 -0.289 0.500 0.488 100 105 110 fitted(m2.43) 115 120 3 > ranef( m2.43 ) $`indi:ojo` (Intercept) 1:de 2.4561373 1:iz 2.9175070 2:de -2.9326111 2:iz -0.3950774 3:de 4.5094506 3:iz 2.4332866 4:de 1.9858642 4:iz -0.3209847 5:de 0.5471502 5:iz 0.5471502 6:de -12.6100267 6:iz 4.7604217 7:de -2.2951612 7:iz -1.6031065 $indi (Intercept) 1 1.7971497 2 -1.1129047 3 2.3219136 4 0.5567986 5 0.3659754 6 -2.6252045 7 -1.3037280 > x11() > qqnorm(ranef( m2.43 )$"indi:ojo"[[1]]) > qqline(ranef( m2.43 )$"indi:ojo"[[1]], lty=3) -5 -10 Sample Quantiles 0 5 Normal Q-Q Plot -1 0 1 Theoretical Quantiles 4 El individuo 6 podría ser un outlier. Repetimos los ajustes anteriores excluyendo al individuo 6 de los análisis. > visionsin6 <- vision[vision$indi!=6,] > m1sin6 <- lmer( agudeza ~ luz + (1|indi), data=visionsin6 ) > summary( m1sin6 ) Linear mixed model fit by REML Formula: agudeza ~ luz + (1 | indi) Data: visionsin6 AIC BIC logLik deviance REMLdev 249.3 260.5 -118.6 245.3 237.3 Random effects: Groups Name Variance Std.Dev. indi (Intercept) 13.9675 3.7373 Residual 7.4973 2.7381 Number of obs: 48, groups: indi, 6 Fixed effects: Estimate Std. Error t value (Intercept) 113.167 1.718 65.86 luz2 1.333 1.118 1.19 luz3 1.417 1.118 1.27 luz4 4.333 1.118 3.88 Correlation of Fixed Effects: (Intr) luz2 luz3 luz2 -0.325 luz3 -0.325 0.500 luz4 -0.325 0.500 0.500 > m2sin6 <- lmer( agudeza ~ luz + (1|indi) + (1|indi:ojo), data=visionsin6 ) > summary( m2sin6 ) Linear mixed model fit by REML Formula: agudeza ~ luz + (1 | indi) + (1 | indi:ojo) Data: visionsin6 AIC BIC logLik deviance REMLdev 251.3 264.4 -118.6 245.3 237.3 Random effects: Groups Name Variance Std.Dev. indi:ojo (Intercept) 0.0000 0.0000 indi (Intercept) 13.9673 3.7373 Residual 7.4973 2.7381 Number of obs: 48, groups: indi:ojo, 12; indi, 6 Fixed effects: Estimate Std. Error t value (Intercept) 113.167 1.718 65.86 luz2 1.333 1.118 1.19 luz3 1.417 1.118 1.27 luz4 4.333 1.118 3.88 Correlation of Fixed Effects: (Intr) luz2 luz3 luz2 -0.325 luz3 -0.325 0.500 luz4 -0.325 0.500 0.500 5 Es de interés observar que al excluir al individuo 6 de los análisis, sólo nos quedan seis individuos en juego, el mismo número que parámetros hay en m1sin6. Por ello m2sin6 es redundante y R “olvida” el último término, dando lugar al mismo ajuste que m1sin6; basta comprobar que su deviance, así como los efectos aleatorios y los fijos son iguales. Solo cabe decir que harían falta más observaciones para extraer alguna conclusión razonable. 6






