Respuestas Caida Libre 1º Parte

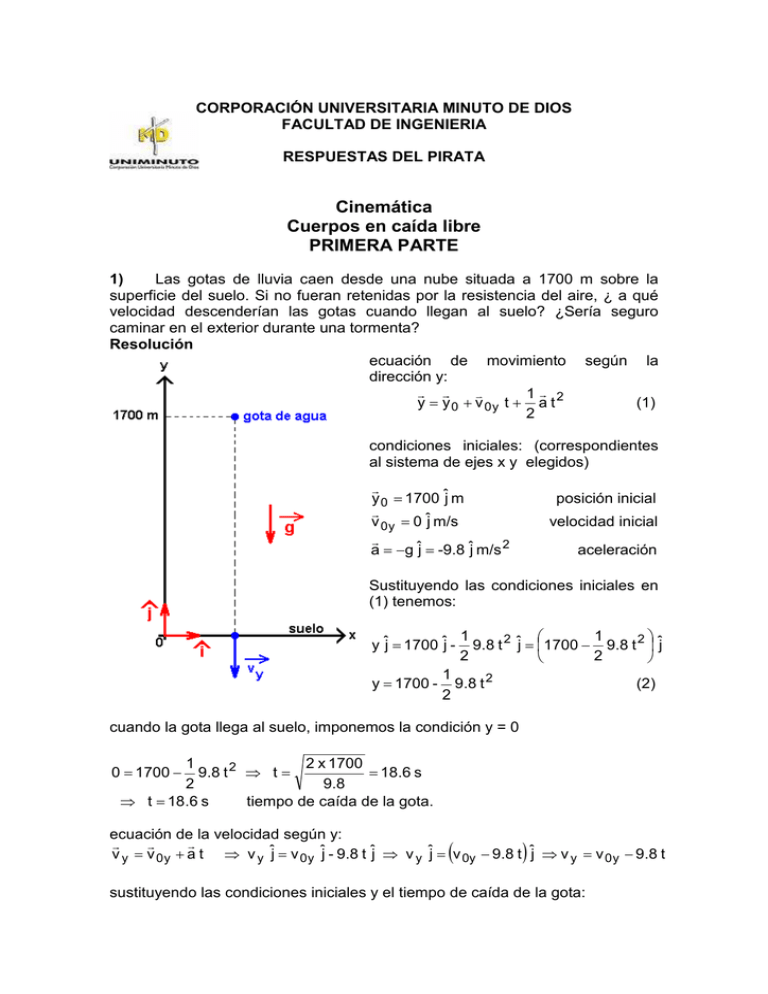
CORPORACIÓN UNIVERSITARIA MINUTO DE DIOS
FACULTAD DE INGENIERIA
RESPUESTAS DEL PIRATA
Cinemática
Cuerpos en caída libre
PRIMERA PARTE
1)
Las gotas de lluvia caen desde una nube situada a 1700 m sobre la
superficie del suelo. Si no fueran retenidas por la resistencia del aire, ¿ a qué
velocidad descenderían las gotas cuando llegan al suelo? ¿Sería seguro
caminar en el exterior durante una tormenta?
Resolución
ecuación de movimiento según la
dirección y:
r r
v
1r
y = y 0 + v 0y t + a t 2
(1)
2
condiciones iniciales: (correspondientes
al sistema de ejes x y elegidos)
r
y 0 = 1700 ĵ m
r
v 0 y = 0 ĵ m/s
r
a = −g ĵ = -9.8 ĵ m/s 2
posición inicial
velocidad inicial
aceleración
Sustituyendo las condiciones iniciales en
(1) tenemos:
y ĵ = 1700 ĵ y = 1700 -
1
1


9.8 t 2 ĵ = 1700 − 9.8 t 2  ĵ
2
2


1
9 .8 t 2
2
(2)
cuando la gota llega al suelo, imponemos la condición y = 0
1
2 x 1700
9 .8 t 2 ⇒ t =
= 18.6 s
2
9.8
⇒ t = 18.6 s
tiempo de caída de la gota.
0 = 1700 −
ecuación de la velocidad según y:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0 y ĵ - 9.8 t ĵ ⇒ v y ĵ = v 0y − 9.8 t ĵ ⇒ v y = v 0 y − 9.8 t
(
)
sustituyendo las condiciones iniciales y el tiempo de caída de la gota:
v y = −9.8 x 18.6 = 182.3 m/s = 655 Km/s
2)
En una obra en construcción una llave cae y golpea el suelo con una
velocidad de 24.0 m/s.
a)
¿Desde qué altura cayo la llave?
b)
¿Cuánto tiempo estuvo en el aire?
b) Ecuación de la rvelocidad según y:
r
r
v y = v 0y + a t
(1)
Condiciones iniciales:
r
v 0 y = 0 m/s
r
a = −g ĵ = -9.8 ĵ m/s 2
velocidad inicial
aceleración
sustituyendo las condiciones iniciales en
(1) tenemos:
v y ĵ = -g t ĵ ⇒ v y = − g t = -9.8 t
(2)
cuando la llave llega al suelo tenemos:
r
v y = − 24.0 ĵ m/s
(3)
Sustituyendo (3) en (2):
- 24.0
− 24.0 = −9.8 t ⇒ t =
= 2 .5 s
- 9.8
⇒ t = 2.5 s
tiempo de caída de la llave
a) Ecuación de movimiento según y
r r
v
1r
y = y 0 + v 0y t + a t 2
2
Condiciones iniciales:
r
y 0 = y 0 ĵ m
r
v 0 y = 0 m/s
r
a = −g ĵ = −9.8 ĵ m/s 2
(4)
velocidad inicial
aceleración
Sustituyendo las condiciones iniciales en (4):
y ĵ = y 0 ĵ −
1
1 2
1


g t ĵ =  y 0 − g t 2  ĵ ⇒ y = y 0 − g t 2
2
2
2


Cuando la llave llega al suelo, imponemos la condición y = 0:
(5)
1
1
9.8 (2.5) 2 ⇒ y 0 = 9.8 (2.5) 2 = 30.6 m
2
2
⇒ y 0 = 30.6 m
altura desde la cual cayó la llave
0 = y0 −
3)
a) ¿A qué velocidad debe ser arrojada una pelota verticalmente hacia
arriba para que llegue a una altura máxima de 53.7 m?
b)
¿Cuánto tiempo estuvo en el aire?
a)
Datos:
r
y 0 = 0 ĵ m
posición inicial
r
y f = 53.7 ĵ m
posición final
r
v f = 0 ĵ m/s
velocidad final
r
a = −g ĵ = -9.8 ĵ m/s 2
aceleración
de acuerdo a los datos de que
disponemos aplicamos la ecuación:
v 2 = v 02 + 2 a ( y − y 0 )
cuando llegue al punto más alto:
0 = v 02 − 2 x 9.8 x (53.7 - 0 )
⇒ v 0 = 2 x 9.8 x 53.7 = 32.4 m/s
por lo tanto: ⇒ v 0 = 32.4 m/s
b)
velocidad a la que debe ser arrojada la pelota
Ecuación de la velocidad según y:
r
r
r
v y = v 0y + a t
r
v 0 y = 32.4 ĵ m/s
r
a = −g ĵ = -9.8 ĵ m/s 2
r
Cuando llegue al punto más alto:
v y = 0 ĵ m/s
(1)
Condiciones iniciales:
Sustituyendo las condiciones iniciales y la condición (2) en (1):
0 ĵ = 32.4 ĵ - 9.8 t ĵ ⇒ 0 = 32.4 - 9.8 t ⇒ t =
⇒ t = 3.3 s
- 32.4
= 3 .3 s
− 9 .8
tiempo que estuvo en el aire
(2)
4)
Una roca es arrojada desde un acantilado de 100 m de altura.
a)
¿Cuánto tiempo demora en caer los primeros 50 m?
b)
¿Cuánto tiempo tarda en caer los segundos 50 m?
Resolución
a)
Ecuación de movimiento según
la dirección y:
r r
v
1r
y = y 0 + v 0y t + a t 2
(1)
2
Condiciones iniciales:
r
y 0 = 100 ĵ m
r
v 0y = 0
r
a = −g ĵ = 9.8 ĵ m/s 2
Sustituyendo las condiciones iniciales
en (1):
1
y = y0 − g t2
2
Cuando llega a y = 50 m tendremos:
50 = 100 −
t=
por lo tanto: t = 3.2 s
1
9. 8 t 2
2
2(50 − 100 )
= 3 .2 s
− 9 .8
tiempo que demora en caer los primeros 50 m
OJO!! Cuando llega a los 50 m tiene una cierta velocidad que hay que calcular
previamente para saber cuanto demora en caer los siguientes 50 metros.
r
r
r
ecuación de la velocidad: v y = v 0 y + a t ⇒ v y ĵ = -g t ĵ ⇒ v y = − g t = -9.8 t
⇒ v y = − g t = -9.8 t
(1)
r
condiciones iniciales: v 0 y = 0
r
a = −g ĵ = 9.8 ĵ m/s 2
sustituyendo las condiciones iniciales en (1)
v 1 = −9.8 x 3.2 = - 31.4 m/s ⇒ velocidad que tiene la llave cuando pasa por la
altura de 50 m.
r r
v
1r
Ecuación de movimiento en y: y = y 0 + v 0 y t + a t 2
2
r
r
Condiciones iniciales: y = 0
y 0 = 50 ĵ m
r
r
v 0 = v 1 = - 31.4 ĵ m/s
Cuando la llave llega al suelo (recorriendo los últimos 50 m):
1
0 = 50 − 31.4 t − 9.8 t 2 ⇒ 0 = 4.9 t 2 + 31.4 t − 50
(ec de 2do grado en t)
2
− 31.4 ± (31.4)2 − 4 x 4.9 x ( −50) − 31.4 ± 44.3
t=
=
2 x 4.9
9 .8
entonces: t = 1.3 s
La otra solución t = – 7.7 s es un valor negativo y por lo tanto un tiempo
negativo no tiene sentido físico.
Por lo tanto:
t = 1.3 s
tiempo que demora en caer los últimos 50 m
5)
Una pelota es arrojada verticalmente hacia abajo a una velocidad inicial
de 20.5 m/s desde una altura de 58.8 m.
a)
¿Cuál será su velocidad cuando llegue al suelo?
b)
¿Cuánto tiempo le lleva a la pelota llegar al suelo?
c)
¿Cuáles serían las respuestas a las partes (a) y (b) si la pelota fuese
arrojada verticalmente hacia arriba desde la misma altura y con la misma
velocidad inicial?
Resolución
b) Ecuación del movimiento según y:
r r
v
1r
y = y 0 + v 0y t + a t 2
(1)
2
Condiciones iniciales:
r
y 0 = 58.8 ĵ m
v
v 0 y = −20.5 ĵ m/s
r
a = −g ĵ m/s 2
Cuando llega al suelo: ⇒ y = 0
posición
velocidad
aceleración
Sustituyendo
las
condiciones
iniciales en (1) tenemos:
1
y ĵ = 58.8 ĵ − 20.5 t ĵ − 9.8 t 2 ĵ
2
1
⇒ y = 58.8 − 20.5 t − 9.8 t 2
(2)
2
(3)
1
Imponiendo la condición (3) en (2): ⇒ 0 = 58.8 − 20.5 t − 9.8 t 2
2
4.9 t 2 + 20.5 t − 58.8 = 0
(ec de 2do grado en t)
− 20.5 ± ( −20.5) 2 − 4 (4.9) ( −58.8 ) − 20.5 ± 1572.7 − 20.5 ± 39.4
t=
=
=
2 x 4.9
9 .8
9 .8
t = −6 .1 s
t = 1. 9 s
no tiene sentido físico
⇒ t = 1.9 s tiempo que demora la pelota en llegar al suelo
(4)
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ
Sustituyendo las condiciones iniciales y el resultado (4) en (3) tenemos:
(3)
a) Ecuación de la velocidad:
⇒ v y = −20.5 − 9.8 x 1.9 = −39 m/s
⇒ v y = −39 m/s
velocidad con que llega al suelo, el hecho de que la
velocidad sea negativa significa que la velocidad apunta hacia el suelo, o sea
en sentido contrario al versor ĵ .
c) Ecuación de la velocidad:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ (5)
Condiciones iniciales:
r
y 0 = 58.8 ĵ m
v
v 0 y = +20.5 ĵ m/s
r
a = −9.8 ĵ m/s 2
posición
velocidad
aceleración
Sustituyendo las condiciones iniciales en (5):
v y = +20.5 − 9.8 t
(6)
Cuando llegue a la altura máxima su velocidad será cero, entonces,
imponiendo v y = 0 en (6) tenemos:
- 20.5
= 2.09 s
- 9.8
tiempo que demora en llegar hasta el punto de altura máxima.
0 = +20.5 − 9.8 t ⇒ t =
t = 2.09 s
Cuando empieza a caer, desde su altura máxima hasta el punto de
altura 58.8 m, el tiempo de caída será de 2.09 s.
A su vez el tiempo de caída desde los 58.8 m hasta el suelo es de 1.9 s
según lo calculado en la parte (b).
Por lo tanto el tiempo total desde que es arrojado hacia arriba hasta que llega
al suelo es:
t TOTAL = 2 x 2.09 + 1.9 = 6.08 s
⇒ t TOTAL = 6.08 s
tiempo total que demora en llegar al suelo.
Para calcular la velocidad con que llega al suelo, consideramos el
problema como el de una pelota que es lanzada con velocidad inicial cero,
sabiendo que el tiempo de caída es: t CAIDA = 2.09 + 1.9 = 3.99 s
r
r
r
Ecuación de la velocidad:
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ
v
Condiciones iniciales: v 0 y = 0 ĵ m/s
velocidad
r
a = −9.8 ĵ m/s 2
aceleración
t CAIDA = 3.99 s
(7)
Sustituyendo las condiciones iniciales en (7) tenemos:
v y = 0 − 9.8 x 3.99 = − 39 m/s
Por lo tanto, la velocidad con la cual la pelota llega al suelo es: v y = −39 m/s
OBSERVACIÓN – Note que la velocidad con la que llega al suelo es la misma
en ambos casos, como explica esto?
6)
Una pelota arrojada hacia arriba tarda 2.25 s en llegar a una altura de
36.8 m.
a)
¿Cuál fue la velocidad inicial de la pelota?
b)
¿Cuál es la velocidad cuando llega a la altura de 36.8 m?
c)
¿Cuál es la altura máxima que alcanzará la pelota?
Resolución
a) Ecuación de movimiento en la
dirección y:
r r
v
1r
y = y 0 + v 0y t + a t 2
2
1 2
y ĵ = y 0 ĵ + v 0 y t ĵ + a t ĵ
(1)
2
Condiciones iniciales:
r
y 0 = 0 ĵ m
posición inicial
r
y = 36.8 ĵ m
posición final
r
a = −g ĵ = −9.8 ĵ m/s 2
aceleración
t = 2.25 s
tiempo de subida
Sustituyendo
iniciales en (1):
las
condiciones
36.8 = 0 + v 0 y (2.25) −
36.8 = v 0 y (2.25) −
1
9.8 (2.25) 2
2
1
9.8 (2.25) 2
2
36.8 = v 0 y (2.25) − 24.8
36.8 + 24.8
= 47.8 m/s
2.25
velocidad inicial de la pelota, el signo positivo
⇒
Por lo tanto: v 0 y = 47.8 m/s
v 0y =
de la velocidad significa que ésta apunta según el versor ĵ
b)
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ
Ecuación de la velocidad:
v y = v 0y − g t
(2)
condiciones iniciales: v 0 y = 47.8 m/s
g = 9.8 m/s 2
t = 2.25 s
Sustituyendo las condiciones iniciales en (2): v y = 47.8 − 9.8 x 2.25 = 25.8 m/s
v
Por lo tanto: v y = 25 .8 ĵ m/s
velocidad de la pelota cuando llega a la altura
de 36.8 m.
v
Cuando la pelota llega a su altura máxima, la condición es: v y = 0 ĵ m/s
y considerando que la pelota fue lanzada desde el suelo con una velocidad ,
puede utilizarse la ecuación de la velocidad para determinar el tiempo en el
cual la pelota llega a su altura máxima.
c)
0 = 47.8 − 9.8 x t ⇒ t =
- 47.8
= 4 .9 s
- 9.8
tiempo en que llega a la altura máxima
Sustituyendo en la ecuación de movimiento (1) tendremos:
1
y = 47.8 x 4.9 − x 9.8 x (4.9) 2 = 116.6 m
2
Por lo tanto: y = 116.6 m
altura máxima que alcanza la pelota
7)
Se dejan caer dos esferas, desde distintas alturas; una se arroja 2.2 s
después de la otra. Si las dos llegan al suelo al mismo tiempo, 4.0 s después
de haber sido arrojada la primera esfera, ¿desde qué altura se dejaron caer
cada una de ellas?
Resolución
Ec de movimiento en y:
r r
v
1r
y = y 0 + v 0y t + a t 2
2
y ĵ = y 0 ĵ + v 0y t ĵ +
y = y 0 + v 0y t +
1 2
a t ĵ
2
1 2
at
2
Condiciones iniciales para la esfera 1:
y=0
cuando llega al suelo
y 0 = H1 m
altura desde la cual fue lanzada.
v 0y = 0
velocidad inicial con que fue lanzada
a = −9.8 m/s 2
t = 4 .0 s
aceleración
tiempo de caída.
Sustituyendo las condiciones iniciales en (1):
1
x 9.8 x (4.0) 2 ⇒ 0 = H1 − 78.4 ⇒ H1 = 78.4 m
2
Por lo tanto: ⇒ H1 = 78.4 m
altura desde la cual cayó la esfera 1
0 = H1 −
Condiciones iniciales para la esfera 2:
y=0
cuando llega al suelo
altura desde la cual fue lanzada.
y 0 = H2 m
(1)
v 0y = 0
velocidad inicial con que fue lanzada
a = −9.8 m/s 2
aceleración
t = (4.0 - 2.2) s = 1.8 s
tiempo de caída (pues la letra dice que la segunda
pelota es lanzada 2.2 segundos después dela primera)
Sustituyendo las condiciones iniciales en (1):
1
0 = H2 − x 9.8 x (1.8) 2 ⇒ 0 = H2 − 15.88 ⇒ H2 = 15.9 m
2
Por lo tanto: ⇒ H2 = 15.9 m
altura desde la cual cayó la esfera 2
8)
Un cohete es disparado verticalmente y asciende con una aceleración
vertical constante de 20 m/s2 durante 1 min. Su combustible se agota entonces
totalmente y continúa como una partícula en caída libre.
a)
¿Cuál es la altura máxima alcanzada?
b)
¿Cuál es el tiempo total transcurrido desde el despegue hasta que el
cohete regresa a la Tierra?
Resolución
a)
Análisis del movimiento: el cohete es lanzado con una velocidad inicial cero en
dirección vertical (esto se asume de la letra pues dice: “es disparado
verticalmente”, en caso de que tuviese alguna velocidad inicial debería dar el
valor o dar algún dato como para calcularlo); con una aceleración constante
que en este caso es una aceleración en la dirección vertical positiva (de otra
forma el cohete nunca podría subir). Cuando se le acaba el combustible el
cohete tiene una cierta velocidad en la dirección positiva que es la que obtuvo
como consecuencia del movimiento previo en el cual tenia una aceleración
positiva. La segunda parte del movimiento va a estar dominada únicamente por
la aceleración de la gravedad, ahora como el cohete ya traía una cierta
velocidad va a seguir subiendo hasta que la gravedad haga que su velocidad
disminuya a cero y ahí empezara a caer hasta llegar al suelo.
Primera parte del movimiento:
Ecuación del movimiento según la dirección y:
r r
v
1r
1
y = y 0 + v 0 y t + a t 2 = y 0 ĵ + v 0y t ĵ + a t 2 ĵ ⇒
2
2
y = y 0 + v 0y t +
condiciones iniciales:
y0 = 0 m
v 0 y = 0 m/s
r
a = +20.0 ĵ m/s 2 ⇒ a = +20.0 m/s 2
t = 1 min = 60 s
1 2
at
2
(1)
posición inicial
velocidad inicial
aceleración
tiempo de subida
sustituyendo las condiciones iniciales en (1) obtendremos la altura hasta la cual
llegó el cohete cuando se le agoto el combustible:
H1 =
1
x 20.0 x (60) 2 = 36000 m
2
Ecuación de la velocidad según la dirección y:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ ⇒ v y = v 0 y + a t
(2)
sustituyendo las condiciones iniciales en (2) obtendremos la velocidad del
cohete cuando se le acaba el combustible:
v 1 = 20.0 x 60 = 1200 m/s
Por lo tanto cuando se acaba el combustible el cohete se encuentra a una
altura de H1 = 36000 m con una velocidad hacia arriba de v1 = 1200 m/s.
Segunda parte del movimiento:
condiciones iniciales:
y 0 = H1 = 36000 m
v 0 y = v 1 = 1200 m/s
r
a = −9.8 ĵ m/s 2 ⇒ a = − 9.8 m/s 2
posición inicial
velocidad inicial
aceleración
sustituyendo en (2) las condiciones iniciales para la segunda parte del
movimiento obtendremos el tiempo durante el cual el cohete sigue
ascendiendo:
v y = v 0 y + a t ⇒ 0 m/s = 1200 m/s − 9.8 m/s 2 x t1
t1 =
(0 − 1200 ) m/s
= 122.5 s
(3)
- 9.8 m/s 2
tiempo durante el cual continua subiendo una vez acabado el combustible.
Sustituyendo las condiciones iniciales y el resultado obtenido en (3) en (1):
y = y 0 + v 0y t +
1 2
1
a t ⇒ H2 = H1 + v 1 x t1 − g x t12
2
2
⇒ H2 = 36000 m + 1200 m/s x (122.5 s) −
1
9.8 m / s 2 x (122.5 s) 2 = 109469 .4 m
2
Por lo tanto la altura máxima que alcanza es: H2 = 109469.4 m = 109.5 Km
b)
La última parte del movimiento corresponde al cohete que cae en caída
libre desde una altura de H1 + H2 = 145469.4 m con una velocidad inicial cero.
Ecuación de movimiento según la dirección y:
Condiciones iniciales:
y =0m
y 0 = H1 + H2 = 145469.4 m
v 0 y = 0 m/s
a = −9.8 m/s 2
y = y 0 + v 0y t +
1 2
at
2 2
(4)
condición de que llega al suelo
altura inicial desde la cual cae
velocidad inicial con la que cae
pues se trata de una caída libre
Sustituyendo las condiciones iniciales en (4):
0 = 145469.4 m -
1
x 9 .8 x t 2 ⇒ t 2 =
2
2 x ( −145469.4)
= 172.3 s
− 9.8
t 2 = 172.3 s
es el tiempo que demora entre caer desde su altura
máxima hasta el suelo.
Tiempo total que estuvo en el aire:
t = 60 s + t1 + t 2 = 60 s + 122.5 s + 172.3 s = 354.8 s
Por lo tanto, tiempo total que estuvo en el aire: ⇒ t = 354.8 s
9)
Una bola se deja caer desde una altura de 2.2 m y rebota a una altura de
1.9 m sobre el suelo. Suponga que la bola está en contacto con el suelo
durante 96 ms.
Determine la aceleración promedio, en magnitud y dirección, de la bola durante
su contacto con el suelo.
Resolución
Aclaración: los puntos A y B del dibujo corresponden al mismo punto. La
pelota cae desde 2.2 m, rebota y
asciende hasta 1.9 m. En el dibujo se
representan por separado para mayor
claridad.
Ecuación del movimiento según la
dirección y:
r r
v
1r
y = y 0 + v 0y t + a t 2 =
2
1
= y 0 ĵ + v 0y t ĵ + a t 2 ĵ
2
y = y 0 + v 0y t +
1 2
at
2
(1)
Condiciones iniciales:
s
y 0 = 2.2 ĵ m ⇒ y 0 = 2.2 m
posición inicial
r
y = 0 ĵ m
posición final
r
v 0 y = 0 m/s
velocidad inicial
r
a = − g ĵ = −9.8 ĵ m/s 2
aceleración
Sustituyendo las condiciones iniciales en (1) obtendremos el tiempo de caída
de la bola:
1
2 x 2.2m
0 = 2.2 m − 9.8 m/s 2 x t 2 ⇒ t 2 =
= 0.45 s 2 ⇒ t = 0.67 s
2
2
9.8 m/s
⇒ t = 0.67 s
tiempo de caída de la bola.
Ecuación de la velocidad según y:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ ⇒ v y = v 0 y + a t
condiciones iniciales: v 0 y = 0
(2)
a = − g = −9.8 m/s 2
sustituyendo las condiciones iniciales en (2) obtendremos la velocidad, v1, con
la cual la bola llega al suelo:
v1 = −9.8 x 0.67 = − 6.56 m/s
el signo negativo indica que la velocidad apunta en dirección contraria al versor
ĵ .
Cuando la pelota sube hasta 1.9 m tendremos: v 2 = v 02 − 2 a ( y − y 0 )
donde: v = 0 , a = −9.8 m/s 2 , ( y − y 0 ) = 1.9 m
⇒ 0 = v 22 − 2 x 9.8 x 1.9 = v 22 − 37.24 ⇒ v 2 = 6.10 m / s
la velocidad v2 es la velocidad con la cual la pelota sale del suelo luego de
haber rebotado, el hecho de que esta velocidad sea positiva significa que esta
dirigida en la misma dirección del versor ĵ
La aceleración durante el contacto con el
suelo estará dada por:
r
r
r v 2 − v 1 6.1 ĵ − ( −6.6 ĵ ) m/s
12.7 m/s
a=
=
=
t 2 − t1
− 96 x 10 - 3 s
− 96 x 10 - 3 s
Por lo tanto la
r
a = −132.3 ĵ m/s 2
aceleración
durante
el
golpe
contra
el
suelo
es:
10) Un paracaidista, después de saltar, cae 52.0 m sin fricción. Cuando se
abre el paracaídas, desacelera a razón de 2.10 m/s2 y llega al suelo con una
velocidad de 2.90 m/s.
a)
¿Cuánto tiempo estuvo el paracaidista en el aire?
b)
¿A qué altura comenzó la caída?
Resolución
a) Primera parte del movimiento
corresponde a una caída libre con
aceleración:
r
a = −g ĵ = -9.8 ĵ m/s 2
Datos: H2 – H1 = 52.0 m
v0 = 0
Utilizamos la relación:
v 2 = v 02 + 2 a d
v 22 = 2 x 9.8 x 52 = 1019.2
⇒ v 2 = 31.9 m / s
Ecuación de la velocidad:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ ⇒ v y = v 0 y + a t
Considerando: v 0 y = 0 , v y = v 2 = −31.9 m/s
31.9
= 3.25 s
tiempo que transcurre entre H1 y H2
9.8
Segunda parte del movimiento
r
r
Condiciones iniciales: v 0 y = v 2 = −31.9 ĵ m/s
velocidad inicial
r
a = +2.10 ĵ m/s 2
aceleración
r
v 3 = −2.90 ĵ m/s
velocidad final
− 31.9 = −9.8 t ⇒ t =
Usando la ecuación de velocidad:
r
r
r
v y = v 0 y + a t ⇒ v y ĵ = v 0y ĵ + a t ĵ ⇒ v 3 = v 2 + a t
v − v 2 − 2.9 + 31.9
t= 3
=
= 14.5 s
a
2.10
tiempo que transcurre de H2 al suelo.
Usando la ecuación del movimiento:
r r
v
1r
1
1
y = y 0 + v 0 y t + a t 2 = y 0 ĵ + v 0y t ĵ + a t 2 ĵ ⇒ y = y 0 + v 0y t + a t 2
2
2
2
cuando llega al suelo, imponemos la condición y = 0
0 = H2 − 31.9 (14.5) +
1
2.10 (14.5) 2 ⇒ H2 = 241.7 m
2
Por lo tanto:
t = 3.25 + 14.5 = 17.75 s
H1 = H2 + 52 m = 293.7 m
tiempo total que estuvo en el aire
altura desde la que comenzó la caída