LECCIÓN 8: ÁTOMOS POLIELECTRÓNICOS Objetivos de la

Lección 8 Química Física (Curso 2010-11)
LECCIÓN 8: ÁTOMOS POLIELECTRÓNICOS
Objetivos de la Lección.
Funciones de onda simétricas y antisimétricas. Principio de exclusión de Pauli. El átomo de He.
Determinantes de Slater. Orbitales aproximados de Slater. Principio de Construcción y Configuración
electrónica. Momento angular en átomos polielectrónicos. Interacciones spin-orbital. Estructura
energética y espectros de átomos polielectrónicos.
Apéndice 8.1: Construcción de términos espectroscópicos.
Apéndice 8.2: Efecto Zeeman.
Cuestiones. Problemas.
OBJETIVOS DE LA LECCIÓN.
En la lección 2 se dejo pendiente uno de los postulados de la Mecánica Cuántica, aquel que
afectaba a sistemas con más de una partícula. Este principio, denominado de antisimetría, o principio
de exclusión de Pauli, será estudiado en esta lección.
El principio de antisimetría, fija el tipo de funciones de onda válidas en sistemas
polielectrónicos. La aplicación de este principio a funciones de onda construidas según la
aproximación de electrones independientes, y que posteriormente serán utilizadas para el cálculo de
energía mediante métodos aproximados, permite deducir que las energías de los estados dependen de
la repulsión entre electrones, así como del valor de los números cuánticos L y S.
La influencia de los números cuánticos L y S en la energía de los estados puede analizarse de
forma conjunta a través del número cuántico J. Dicho análisis se efectúa de forma cualitativa a través
de las denominadas interacciones Spin-Orbital, o interacciones L-S, a partir de las cuales se definen
los denominados términos espectroscópicos, equivalentes a los niveles de energía del átomo.
Por último, se analizan algunos ejemplos donde se estudiará la estructura electrónica y los
espectros de algunos átomos polielectrónicos sencillos.
169
Lección 8 Química Física (Curso 2010-11)
FUNCIONES DE ONDA SIMÉTRICAS Y ANTISIMÉTRICAS
Las funciones de onda para el átomo de helio, según la aproximación de electrones
independientes, tiene la forma ψαβ = φα(q1)φβ(q2), donde α y β representan dos orbitales cualesquiera
del átomo de hidrógeno, y q1 y q2, son las coordenadas de los dos electrones (ri en el caso más simple).
Hasta donde hemos visto, no existe nada que nos impida colocar dos, o más electrones, en el mismo
orbital. Para que nuestro razonamiento sea general, vamos a suponer que α y β son diferentes, y para
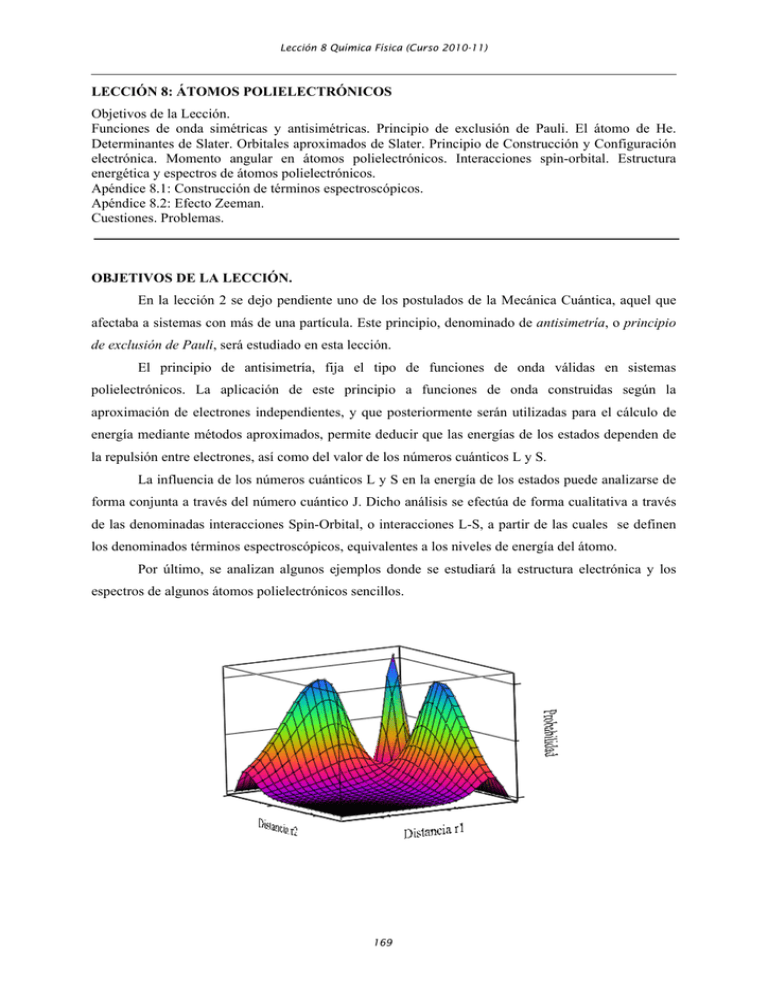
analizar un ejemplo, supondremos que α = 1s y β = 2s. El cuadrado de ψαβ, nos proporciona la
probabilidad de encontrar a cada uno de los electrones en determinadas regiones del espacio, q1 y q2 (o
r1 y r2).
2
P (1, 2 ) = ( ψ αβ ) dτ = ( ψ1s,2s ) dτ = φ1s2 ( r1 ) dτ1 ⋅ φ2s
( r2 ) dτ2 = P1s ( r1 ) P2s ( r2 )
2
2
(8.1)
Es decir, la probabilidad total es el producto de las probabilidades individuales de cada
electrón en el correspondiente orbital atómico. Vamos a suponer, que queremos calcular la
probabilidad de encontrar al electrón 1 a una distancia r1 del núcleo, y simultáneamente al electrón 2 a
una distancia r2. La probabilidad total, será por tanto el producto P(1,2) = P1s(r1) P2s(r2). En la Figura
8.1-a, se muestran las representaciones de P1s(r1), y P2s(r2), y se indican con flechas los valores de
estas funciones para dos distancias concretas r1 y r2, indicando dichas distancias con líneas verticales
rosas.
a)
b)
Probabilidad
Probabilidad
P1s (r1)
15
15
P2s (r1)
P2s (r2)
10
10
P1s (r2)
5
5
0
r1
1
2
3
r2
4
5
6
7
r (D)
0
r1
1
2
r2
3
4
5
6
7
r (D)
Figura 8.1
Arbitrariamente hemos asignado el electrón 1 al orbital 1s, pero nada nos obliga a ello. Vamos
a suponer ahora que el electrón 1 está situado en el orbital 2s, mientras que el 2 lo está en el 1s. De
hecho las probabilidades de encontrar a los electrones a esas distancias, y en dichos orbitales son
diferentes de cero. La asignación realizada ahora se indica mediante; ψβα = φα(q2)φβ(q1) En este caso,
la probabilidad será,
2
P ( 2,1) = ( ψβα ) dτ = ( ψ 2s,1s ) dτ = φ1s2 ( r2 ) dτ2 ⋅ φ2s
( r1 ) dτ1 = P1s ( r2 ) P2s ( r1 )
2
2
(8.2)
En la Figura 8.1-b, se indican los valores de P1s(r2) y P2s(r1) a las mismas distancias que en el
170
Lección 8 Química Física (Curso 2010-11)
caso anterior. Evidentemente, como puede deducirse de la Figuras 8.1, P(1,2) ≠ P(2,1). Es decir, la
probabilidad total es diferente en función de cómo distribuyamos los electrones en los diferentes
orbitales, lo cual es absurdo, ya que los electrones no cambian de sitio, solo los asignamos,
arbitrariamente, a un orbital u otro.
En cualquier caso, la funciones ψαβ = ψ1s,2s = φ1s(r1) φ2s(r2), y ψβα = ψ2s,1s = φ1s(r2) φ2s(r1), son
degeneradas, ya que al ser un sistema formado por partículas independientes, la energía es la suma de
las energías de los orbitales atómicos 1s y 2s. Es decir, tenemos dos funciones que poseen la misma
energía, pero que dan lugar a diferentes probabilidades, luego, ¿Cual es la función correcta?.
De hecho, la pregunta anterior no tiene sentido y deberíamos mejor preguntar; ¿Es posible
distinguir a un electrón del otro?, ¿llevan una etiqueta los electrones que nos indican en todo
momento, que pertenecen al orbital 1s o al 2s?. Evidentemente, no.
Antes de resolver el problema veamos por qué ha surgido dicho problema: Todo parte de que
no se puede resolver de forma analítica la ecuación de Schrödinger de átomos polielectrónicos, Hψ =
Eψ, por lo que se utilizan soluciones aproximadas, del tipo ψ0 = ∏φα(qi), (aproximación de electrones
independientes), de forma que cada electrón es introducido en un orbital atómico del hidrógeno, y al
hacer esto, estamos distinguiendo a los electrones, es decir, estamos poniéndoles etiqueta, y por lo
tanto estamos cometiendo un error. Aunque en Mecánica Clásica las partículas son distinguibles, en
Mecánica Cuántica dos partículas idénticas son indistinguibles.
La necesidad de que las partículas cuánticas sean indistinguibles, se traduce en el
principio que nos dice que; Las propiedades de todo sistema cuántico deben permanecer invariantes
ante el intercambio de dos partículas idénticas. Según esto, cuando en la función de onda del átomo
de He se intercambian de posición los electrones 1 y 2, las propiedades del sistema no deberían
modificarse, y, evidentemente esto no ocurre con las dos funciones anteriores, ya que las
probabilidades que predicen dichas funciones son diferente. Luego, las funciones ψαβ = ψ1s,2s = φ1s(r1)
φ2s(r2), y ψβα = ψ2s,1s = φ1s(r2) φ2s(r1), no son funciones aceptables para describir correctamente la
probabilidad de encontrar a los electrones en el átomo de He.
Volvamos a una situación general, donde α, y β, son dos orbitales atómicos cualesquiera,
representando ψαβ = φα(q1)φβ(q2) una situación en la que introducimos al electrón 1 en el orbital α, y el
2, en el β, mientras que ψβα, representa la situación inversa, en la que electrón 1 se introduce en el
orbital β, y el 2, en el α. Según lo comentado con anterioridad, estas funciones no son aceptables ya
que; (ψαβ)2 ≠ (ψβα)2. Funciones aceptables son las que cumplen que
ψ ( q1 ,q 2 ) = ψ ( q 2 ,q1 )
2
2
⇒ ψ ( q1 ,q 2 ) = ±ψ ( q 2 ,q1 )
(8.3)
Esta relación la tiene que cumplir, no solo la función real desconocida, sino también cualquier
función aproximada que utilicemos (aproximación de electrones independientes). Si en la ecuación
(8.3)(parte derecha), el signo es positivo, se dice que la función es simétrica, y si es negativo,
antisimétrica. Aunque las funciones ψαβ y ψβα no son aceptables, sin embargo, si lo son combinaciones
171
Lección 8 Química Física (Curso 2010-11)
lineales de ellas
ψ s = ψ αβ + ψ βα
ψ a = ψ αβ − ψ βα
⇒ ψ s ( q1 ,q 2 ) = ψ s ( q 2 ,q1 )
⇒ ψ a ( q1 ,q 2 ) = −ψ a ( q 2 ,q1 )
(8.4)
Estas dos funciones si son aceptables desde el punto de vista de que los electrones son
partículas indiscernibles. Además, son funciones degeneradas con ψαβ y ψβα. A esta forma de
introducir degeneración se le denomina degeneración por intercambio. El sentido físico de estas
expresiones consiste en permitir que todos los electrones, al ser indistinguibles, puedan situarse en
todos los orbitales atómicos.
La función de onda total se construye a partir del producto de la función orbital o espacial
(solución de la ecuación de Schrödinger), y de la función de spin
ψ n,A ,m,s,ms = ψ n,A ,m σs,ms = ψ orbital σspin = ( ψ αβ ± ψβα ) σspin
(8.5)
Para un electrón dado, solo existen dos funciones de spin, que corresponden a los valores de
ms = ±1/2. A estas funciones se las denominó en la Lección 6 mediante σ+ y σ-. La función de onda
total debe poseer simetría con respecto al intercambio de electrones, luego, dado que la parte espacial
posee simetría, ψs o ψa, la parte de spin también debe poseer simetría. Con dos funciones y dos
electrones, es posible construir 4 funciones que posean simetría, estas son
σ + (1) σ − ( 2 ) − σ − (1) σ + ( 2 ) ⇒ antisimetrica
σ − (1) σ − ( 2 )
⇒
simetrica
σ + (1) σ + ( 2 )
⇒ simetrica
σ + (1)σ − ( 2 ) + σ − (1)σ + ( 2 ) ⇒ simetrica
(8.6)
La función de onda total se construye multiplicando la parte espacial por la de spin, luego, en
nuestro sistema de dos electrones, vamos a tener 8 funciones posibles, 4 simétricas y 4 antisimétricas.
Las 4 funciones simétricas son:
(ψ
αβ
− ψ βα ) ⎣⎡σ + (1) σ − ( 2 ) − σ − (1)σ + ( 2 ) ⎦⎤
(ψ
(ψ
αβ
αβ
+ ψ βα )σ + (1) σ + ( 2 )
+ ψ βα ) ⎣⎡σ + (1) σ − ( 2 ) + σ − (1) σ + ( 2 ) ⎦⎤
(ψ
αβ
(8.7)
+ ψ βα ) σ − (1) σ − ( 2 )
Mientras que las 4 antisimétricas son:
(ψ
αβ
+ ψ βα ) ⎣⎡σ + (1) σ − ( 2 ) − σ − (1)σ + ( 2 ) ⎦⎤
(ψ
(ψ
αβ
αβ
− ψ βα )σ + (1) σ + ( 2 )
−ψ βα ) ⎣⎡σ + (1) σ − ( 2 ) + σ − (1)σ + ( 2 ) ⎦⎤
(ψ
αβ
− ψ βα ) σ − (1) σ − ( 2 )
Cualquiera de estas 8 funciones cumple el requisito exigido por la ecuación (8.3).
172
(8.8)
Lección 8 Química Física (Curso 2010-11)
PRINCIPIO DE EXCLUSIÓN DE PAULI
El principio de exclusión de Pauli nos dice que; un sistema formado por varios electrones solo
puede estar representado por funciones de onda antisimétricas. Es decir, que de las 8 funciones
anteriores, solo son válidas, para describir el comportamiento del átomo de He, las 4 combinaciones
antisimétricas, ψTotal(q1,q2) = - ψTotal(q2,q1). Estas son
(ψ
(ψ
αβ
+ ψβα ) ⎣⎡σ + (1) σ − ( 2 ) − σ − (1) σ + ( 2 ) ⎦⎤
− ψβα ) σ + (1) σ + ( 2 )
[ 2]
( ψαβ − ψβα ) ⎣⎡σ+ (1) σ− ( 2 ) + σ− (1) σ+ ( 2 )⎦⎤ [3]
[ 4]
( ψαβ − ψβα ) σ− (1) σ− ( 2 )
[1]
αβ
(8.9)
En la primera de estas funciones [1], la parte espacial es simétrica, y los electrones poseen
valores de ms opuestos, se dice en este caso que los electrones son paralelos, o están apareados ( ↑↓ ).
El valor de ms total es Ms = ms(1) + ms(2) = 1/2 - 1/2 = 0 (usaremos letras mayúsculas, Ms, para
indicar la suma de los valores de ms correspondientes a electrones individuales). Como Ms varía entre
± S, el spin total será S = 0. La multiplicidad de un estado se definió en la lección 6 como la relación
2S+1, en nuestro caso 2S+1=1 (singlete). Además, para este caso no existe ninguna restricción para
que α = β, es decir, los dos electrones pueden situarse en el mismo orbital atómico (parte espacial), y
por lo tanto, pueden tener los mismos números cuánticos n, ℓ y m, ya que ms es diferente.
Fijémonos ahora en las funciones [2]-[4] de la ecuación (8.9), para estas tres funciones la parte
espacial es antisimétrica, por lo que si α = β, la función de onda es cero. Es decir, la función de onda
no existe si los dos electrones poseen los mismos números cuánticos n, ℓ y m. Estas tres funciones
deben ser analizadas conjuntamente ya que poseen la misma parte espacial. En la función [2], Ms = ms
(1) + ms(2) = +1/2 +1/2 =1, en la [3], Ms = +1/2 +(-1/2) =0, mientras que en la [4], Ms = -1/2 -1/2 =
-1. Es decir, Ms = 0,±1, por lo que S = 1. Se dice en este caso, que los electrones son antiparalelos o
están desapareados ( ↑↑ ), la multiplicidad es 2S+1 = 3 (hay tres estados degenerados, estado triplete).
En este último caso, los dos electrones poseen el mismo valor de ms, y como ψαβ ≠ ψβα, se llega a la
conclusión de que los dos electrones no pueden tener sus 4 números cuánticos iguales, ya que en dicho
caso, la función de onda es cero. Esta es una conclusión del principio de exclusión de Pauli, que con
frecuencia se suele enunciar como el propio principio.
Supongamos que las funciones de onda simétricas son también válidas para el átomo de He.
Elijamos para ello, por ejemplo, la segunda de las funciones de la ecuación (8.7). En esta función, los
dos electrones poseen el mismo valor de ms, y además, nada impide que α = β, es decir, los dos
electrones pueden tener sus 4 números cuánticos iguales, en contra de la evidencia experimental.
El hecho de que el movimiento de los electrones deba estar representado por funciones de
onda antisimétricas tiene que ver con el valor de su spin. Las partículas que poseen spin semientero se
denominan Fermiones (electrón, neutrón etc.), y estas partículas llevan asociadas funciones de onda
173
Lección 8 Química Física (Curso 2010-11)
antisimétricas, o lo que es lo mismo, dos partículas no pueden tener los mismos números cuánticos, y
por lo tanto no pueden situarse en el mismo estado.
Las partículas con spin entero se denominan Bosones (fotón), y estas llevan asociadas
en su movimiento funciones de onda simétricas, por lo que para ellas no se cumple el principio de
exclusión de Pauli, es decir dos o más partículas pueden tener todos sus números cuánticos iguales,
pudiendo situándose en el mismo estado. Un ejemplo es la luz monocromática.
Las conclusiones del principio de exclusión son de enorme importancia, pero hay que
recordar que necesitamos este principio para corregir las funciones de onda obtenidas mediante la
aproximación de electrones independientes. Estas funciones no son las funciones reales del átomo. Si
se pudiera resolver la ecuación de Schrödinger para átomo polielectrónicos este principio no sería
necesario, ya que estaría implícito en las soluciones obtenidas.
174
Lección 8 Química Física (Curso 2010-11)
EL ÁTOMO DE HELIO
Vamos a analizar los primeros niveles de energía del átomo de He, partiendo de la
aproximación de electrones independientes. En el estado fundamental, la configuración electrónica es
1s 2 , lo que implica que debemos utilizar una parte espacial simétrica y por tanto, una de spin
antisimétrica. Dicha función tendrá la forma
ψ 0 = N ⎣⎡φ1s (1) φ1s ( 2 ) + φ1s ( 2 ) φ1s (1) ⎦⎤ ⎣⎡σ+ (1) σ− ( 2 ) − σ− (1) σ+ ( 2 ) ⎦⎤ =
= φ1s (1) φ1s ( 2 ) ⎣⎡σ+ (1) σ − ( 2 ) − σ− (1) σ+ ( 2 ) ⎦⎤
(8.10)
Donde la constante de normalización, en la última de las expresiones, vale 1, suponiendo que
los orbitales atómicos están a su vez normalizados. En este estado los electrones están apareados
( ↑↓ ), es decir S = 0. Vamos a aplicar el método de variaciones para calcular la energía aproximada de
este estado. La función de spin no depende de las coordenadas, actuando como una constante que para
simplificar no escribiremos, por lo tanto
φ (1) φ1s ( 2 )
ψ 02
dτ = 2E1s + ∫ 1s
dτ =2E1s + J1s,1s
r12
r12
2
E 0 = ∫ ψ 0 Hψ 0 dτ = ∫ ψ 0 H 0 ψ 0 dτ + ∫
2
(8.11)
Las integrales del tipo:
φα (1) φβ ( 2 )
2
∫
2
dτ =J α ,β
r12
(8.12)
se denominan integrales de Coulomb. Estas son integrales bielectrónicas. En el apéndice 7.1 se
describió como se determinan. En la Tabla 8.1, se proporcionan los valores para algunas integrales
sencillas de este tipo.
α
β
Jα,β
α
β
Kα,β
1s
1s
5
Z
8
1s
1s
J1s,1s
1s
2s
17
Z
81
1s
2s
16
Z
729
1s
2p
59
Z
243
1s
2p
112
Z
6561
Tabla 8.1
Las integrales de Coulomb tienen unidades de energía, y en la tabla están expresadas en
unidades atómicas. Si se substituye en la ecuación 8.11, la energía aproximada del estado fundamental
del He será:
E 0 = 2E1s + J1s,1s = −2
Z2 5
10
+ Z = −4 + = −2.75
2n 2 8
8
u.a.
(8.13)
Experimentalmente la energía es −2.905 u.a, como ya sabemos. En la Figura 8.2, se muestra
175
Lección 8 Química Física (Curso 2010-11)
un diagrama, en el que se representan las energías de los primeros estados del átomo de He.
1s 12p1
1s 12s 1
S=0 E2S=-2.124
3
S=1E2T=-2.135 ψ2T = 2 P2,1,0
E =-2.146 ψ1S = 21 S0
S=0 1S
S=1 E =-2.176 ψ = 23S
1T
1
1T
S=0
1s 2
ψ2S = 21P1
E0=-2.905
ψ0 = 11S0
Figura 8.2
La primera configuración electrónica excitada del He es; 1s1 2 s1 . Al ser los orbitales diferentes
tenemos dos opciones que consisten en usar funciones de onda espaciales simétricas, o antisimétricas.
Llamemos ψ1T, a la función que se construye con una parte espacial antisimétrica, por lo que S =1, y
los electrones están desapareados (estado triplete, ↑↑ ). Esta función, que en realidad son tres
funciones, tiene la forma:
⎡
σ + (1) σ + ( 2 )
⎤
1
⎢
ψ1T =
( φ1s (1) φ2s ( 2 ) − φ1s ( 2 ) φ2s (1) ) ⎢σ+ (1) σ− ( 2 ) + σ− (1) σ+ ( 2 )⎥⎥
2
⎢⎣
⎥⎦
σ − (1) σ − ( 2 )
(8.14)
El fator 1/21/2, es la constante de normalización. Por otro lado, llamaremos ψ1S, a la función
que posee la parte espacial simétrica, y de spin antisimetrica, por lo que S = 0 ( ↑↓ , estado singlete).
ψ1S =
1
( φ1s (1) φ2s ( 2 ) + φ1s ( 2 ) φ2s (1) ) ⎣⎡σ+ (1) σ− ( 2 ) − σ− (1) σ+ ( 2 )⎦⎤
2
(8.15)
Según la aproximación de electrones independientes, los estados ψ1T, y ψ1S, son degenerados,
sin embargo, cuando se aplica el método de variaciones, sus energías son diferentes, así, ignorando la
parte de spin, para ψ1T;
E1T = ∫ ψ1T Hψ1T dτ = ∫ ψ1T H 0 ψ1T dτ + ∫
2
ψ1T
ψ2
dτ = E1s + E 2S + ∫ 1T dτ
r12
r12
(8.16)
Vamos a analizar la última de estas integrales:
2
ψ1T
1 ( φ1s (1) φ2s ( 2 ) − φ1s ( 2 ) φ2s (1) )
1 φ (1) φ2s ( 2 )
dτ = ∫ 1s
dτ +
∫ r12 dτ = 2 ∫
r12
2
r12
2
2
2
1 φ1s ( 2 ) φ2s (1)
2 φ (1) φ2s ( 2 ) φ1s ( 2 ) φ2s (1)
dτ − ∫ 1s
dτ
∫
2
r12
2
r12
2
2
(8.17)
Las dos primeras integrales son idénticas, y son del tipo de las integrales de Coulomb,
analizadas en la ecuación (8.12)
176
Lección 8 Química Física (Curso 2010-11)
∫
φ1s2 (1) φ22s ( 2 )
r12
dτ = ∫
2
φ1s2 ( 2 ) φ2s
(1)
r12
dτ = J1s,2s
(8.18)
Por otra parte, a las integrales del tipo:
K αβ = ∫
φα (1) φβ ( 2 ) φα ( 2 ) φβ (1)
r12
dτ
(8.19)
se las denomina integrales de intercambio. En la Tabla 8.1, se muestran algunos valores para estas
integrales bielectrónicas, que se resuelven mediante el mismo procedimiento al descrito en el apéndice
7.1. Volviendo a la ecuación (8.16)
E1T = ∫ ψ1T H 0 ψ1T dτ + ∫
2
ψ1T
dτ =E1s + E 2S + J1s,2s − K1s,2s
r12
(8.20)
Por otra parte, si realizamos la misma operación con la función ψ1S, tendremos que
E1S = ∫ψ 1S Hψ 1S dτ = ∫ψ 1S H 0ψ 1S dτ + ∫
ψ 12S
dτ = E1s + E2 S + ∫
r12
ψ 12S
r12
dτ
(8.21)
La última integral, puede escribirse como:
2
2
2
ψ1S
1 ( φ1s (1) φ2s ( 2 ) + φ1s ( 2 ) φ2s (1) )
1 φ1s (1) φ2s ( 2 )
d
τ
=
d
τ
=
dτ +
∫ r12
2∫
r12
2∫
r12
2
1 φ1s ( 2 ) φ2s (1)
2 φ (1) φ2s ( 2 ) φ1s ( 2 ) φ2s (1)
dτ + ∫ 1s
dτ = J1s,2s + K1s,2s
∫
2
r12
2
r12
2
2
(8.22)
Por lo tanto,
E1S = E1s + E2 S + J1s ,2 s + K1s ,2 s
(8.23)
Resultado diferente al obtenido para ψ1T. Teniendo en cuenta que En = -Z2/2n2, y a partir de los
datos de la Tabla 8.1, se obtiene que:
4 4
E1T = − − + 0.420 − 0.044 = −2.124 uaE. Experimentalmente −2.176
2 8
4 4
E1S = − − + 0.420 + 0.044 = −2.036 uaE. Experimentalmente −2.146
2 8
(8.24)
Por lo tanto, la configuración electrónica 1s1 2 s1 , conduce a dos niveles de energía, en función
de que el spin total sea S = 1, o S = 0. En la Figura 8.2, se representan las energías experimentales de
estos estados, que son ligeramente diferentes a las calculadas mediante el método de variaciones.
Para la siguiente configuración electrónica, 1s12p1, se pueden construir dos nuevas funciones
que llamaremos ψ2T, y ψ2S. La forma de estas funciones es:
ψ 2T
ψ 2S
⎡
σ+ (1) σ+ ( 2 )
⎤
⎢
⎥
=
φ1s (1) φ2p ( 2 ) − φ1s ( 2 ) φ2p (1) ) ⎢σ+ (1) σ− ( 2 ) + σ− (1) σ + ( 2 ) ⎥ ↑↑
(
2
⎢⎣
⎥⎦
σ− (1) σ − ( 2 )
1
=
( φ1s (1) φ2p ( 2 ) + φ1s ( 2 ) φ2p (1) ) ⎣⎡σ+ (1) σ− ( 2 ) − σ− (1) σ+ ( 2 )⎦⎤ ↑↓
2
1
(8.25)
Aplicando el método de variaciones, como anteriormente, sus energías aproximadas serán:
177
Lección 8 Química Física (Curso 2010-11)
4 4
E 2T = E1s + E 2p + J1s,2p − K1s,2p = − − + 0.486 − 0.034 = −2.049uaE Exper. −2.135
2 8
(8.26)
E 2S = E1s + E 2p + J1s,2p + K1s,2p = −1.980uaE
Exper. −2.124
En la Figura 8.2, se esquematizan estos diferentes niveles de energía. Con respecto al átomo
de hidrógeno, la energía electrónica en el He está afectada por tres fenómenos nuevos:
* La repulsión electrónica,
* El spin total.
* El valor del número cuántico ℓ.
Es sorprendente que, a pesar de que la ecuación de Schrödinger no predice la aparición del
spin, la energía que se obtiene si es función del spin. Este fenómeno surge del empleo de funciones de
onda que poseen parte espacial simétrica (S = 0), o antisimétrica (S = 1). Un procedimiento cualitativo
para analizar conjuntamente la influencia de ℓ y S en la energía, lo que se denomina interacciones
spin-orbital, se analizará al final de esta lección.
Otra cuestión relacionada con lo anterior consiste en que puede generalizarse que; para una
configuración dada, el estado más estable es siempre el de mayor spin (regla de Hund). Fijémonos, por
ejemplo, en las ecuaciones (8.14) y (8.15), las cuales vamos a escribir de la forma:
ψ1T = N ( φ1s (1) φ2s ( 2 ) − φ1s ( 2 ) φ2s (1) )
ψ1S = N ( φ1s (1) φ2s ( 2 ) + φ1s ( 2 ) φ2s (1) )
S =1
S=0
(8.27)
Donde N es una constante que incluye la función de spin. En la Figura 8.3, se muestran las
representaciones de la función probabilidad (el cuadrado de las funciones), para ambas funciones
frente a r1 y a r2. En la página web: http://www.uco.es/organiza/departamentos/quimica-fisica/quimicafisica/MC/QFL8a.htm, se describe el método para realizar esta representación.
(R1S)2
(R1T)
2
Figura 8.3
178
r1 = r 2
Lección 8 Química Física (Curso 2010-11)
En dicha figura, se observa que la probabilidad de encontrar a los dos electrones juntos, es
decir para r1 . r2 (línea roja en la figura), es cero para el estado ψ1T, y diferente de cero para ψ1S. Es
decir, cuando S = 1, existe una repulsión entre los electrones, adicional a la repulsión de carga (hueco
de Fermi), que hace que sea imposible encontrar a los electrones próximos uno a otro, este fenómeno
estabiliza al orbital. Sin embargo, cuando S = 0, existe una cierta atracción entre los electrones, debido
al acoplamiento de sus spines, por lo que como consecuencia de la repulsión entre cargas, el estado es
más inestable, y es por lo tanto de mayor energía que cuando S = 1.
.
179
Lección 8 Química Física (Curso 2010-11)
DETERMINANTES DE SLATER
Cuando existen más de dos electrones, no podemos construir funciones antisimétricas a mano,
dado lo enormemente laborioso que resulta. Un método general de escribir funciones de onda
antisimétricas es mediante determinantes en los que se utilizan directamente las funciones spin-orbital.
Así, la función ψ0 del He, puede escribirse:
ψ0 =
1 φ1s (1) σ+ (1) φ1s (1) σ− (1)
2 φ1s ( 2 ) σ+ ( 2 ) φ1s ( 2 ) σ− ( 2 )
(8.28)
En la primera columna, se coloca un spin-orbital φ1sσ+, y en la segunda el otro spin-orbital
φ1sσ-, y en cada fila se añade un electrón. En general, la función de onda antisimétrica para el estado
fundamental de un átomo, con n electrones, se puede escribir como
φ1s (1) σ+ (1)
φ1s ( 2 ) σ+ ( 2 )
ψ0 =
φ1s ( 3) σ+ ( 3)
n
"
1
φ1s (1) σ − (1)
φ1s ( 2 ) σ − ( 2 )
φ1s ( 3) σ− ( 3)
"
φ2s (1) σ + (1)
"
φn (1) σ ± (1)
φ2s ( 2 ) σ + ( 2 ) " φn ( 2 ) σ ± ( 2 )
φ2s ( 3) σ + ( 3) " φn ( 3) σ ± ( 3)
"
"
"
(8.29)
φ1s ( n ) σ+ ( n ) φ1s ( n ) σ − ( n ) φ2s ( n ) σ + ( n ) " φn ( n ) σ ± ( n )
La función cambia de signo si se intercambian dos filas (electrones) de posición, lo que indica
su carácter antisimétrico, y es cero, si dos columnas son iguales, es decir, si utilizamos dos spinorbitales con los 4 números cuánticos idénticos. La forma de expresar funciones antisimétricas de
estados excitados de átomos es más compleja, y se necesitan en general sumar varios determinantes.
180
Lección 8 Química Física (Curso 2010-11)
ORBITALES APROXIMADOS DE SLATER
Los orbitales de Slater (STO) son funciones analíticas de fácil manejo que se obtienen a partir
del concepto de carga nuclear efectiva. Este concepto, de forma muy simplificada, consiste en suponer
que los electrones internos apantallan la carga del núcleo, de forma que en la interacción entre el
electrón y el núcleo no interviene su carga real, sino la denominada carga nuclear efectiva, la cual se
determina a partir de una serie de relaciones más o menos empíricas, procedentes de cálculos
variacionales. Los orbitales de Slater, en unidades atómicas, tienen la forma,
ψ n,A ,m = Nr n*−1e − rZ*/ n* YAm
(8.30)
donde N, es una constante de normalización, n*, es el número cuántico principal efectivo, Z*, es la
carga nuclear efectiva, e Yℓm, son las funciones armónicos esféricos. El valor de n*, se determina
sustituyendo el número cuántico principal n = 1, 2, 3, 4, 5, 6, .., por n = 1, 2, 3, 3.7, 4, 4.2, .., y siendo
Z* = Z – Sn,ℓ, donde Sn,ℓ, es la denominada constante de apantallamiento. Esta, se calcula clasificando
los orbitales atómicos en los siguientes grupos
(1s) (2s,2p) (3s,3p) (3d) (4s,4p) (4d) (4f) (5s,5p)....
El valor de Sn,ℓ, para un electrón dado, es la suma de las siguientes contribuciones:
1) 0.35 por cada electrón que exista en el mismo grupo que el considerado, salvo si es el grupo
(1s) en cuyo caso se suma 0.3.
2) Si el electrón considerado es s o p, se suma 0.85 por cada electrón en el grupo
inmediatamente inferior, y 1 por cada electrón más interno. Para el resto de los grupos se suma 1 por
cada electrón interno.
La energía del átomo puede también determinarse, de forma aproximada, mediante la relación
E = −∑ ( Z*i )
2
i
2 ( n *i )
2
(8.31)
Por ejemplo, para el He, Z1s* = 2-0.3 = 1.7, luego EHe = -2 (1.7)2/2 = -2.89 uaE
(experimentalmente EHe = -2.905).
Para el Li, Z1s* = 3-0.3 = 2.7, Z2s* = 3-2×0.85 = 1.3, luego ELi = -2 (2.7)2/2-(1.3)2/8 = -7.501
uaE (experimentalmente EHe = -7.478). Analicemos una cuestión interesante en el caso del átomo de
Li. Cuando la configuración electrónica es la fundamental (1s22s1), la energía del electrón en el orbital
2s es E2s = -(1.3)2/8 = -0.211 uaE. Pero si la configuración electrónica es; 1s12s2, la constante de
apantallamiento de los electrones 2s será 0.85+0.35 = 1.2, luego Z2s* = 3-1.2 = 1.8, y por lo tanto, la
energía de un electrón en un orbital 2s es E2s = -(1.8)2/8 = -0.405 uaE. Es decir, la energía del electrón
en un orbital 2s no es constante como sucedía en el átomo de hidrógeno. Dicha energía depende de la
población del resto de los orbitales (configuración electrónica), y por tanto de la energía de repulsión.
Los orbitales de Slater (OTS o STO en Ingles), se utilizan con frecuencia en sustitución de los
orbitales atómicos (OA) del hidrógeno, para construir orbitales moleculares mediante combinaciones
lineales (CLOST, en vez de CLOA). La razón es que es más fácil resolver las integrales que aparecen
con los OTS. También es frecuente utilizar orbitales atómicos gaussianos (OTG o GTO en Ingles).
181
Lección 8 Química Física (Curso 2010-11)
PRINCIPIO DE CONSTRUCCIÓN Y CONFIGURACIÓN ELECTRÓNICA
El principio de construcción (Aufbau), fue enunciado por Niels Bohr, y permite determinar la
configuración electrónica del átomo en su estado fundamental. Este principio nos dice que: Para
construir la configuración electrónica de un átomo se llenan sus orbitales en orden creciente de n+ ℓ,
y cuando n+ ℓ coincide, se llena primero el orbital de menor n. Sin embargo, este principio falla al
menos para diez átomos, y existen unos 20 átomos para los que no se tiene una certeza clara de su
configuración electrónica. Este principio ha sido completado con la regla de Hund, que nos dice que
un átomo toma la configuración con el mayor número de electrones desapareados.
Un caso típico en el que no se cumple el anterior principio es el del átomo de
Cr(Z=24), cuya configuración electrónica es [Ar]4s13d5. Los átomos anteriores y posteriores
en la tabla periódica tienen una configuración; V(Z=23): [Ar]4s23d3, y Mn(Z=25): [Ar]4s23d5.
Según el principio de construcción, un orbital 4s (n+ ℓ = 4), debe llenarse antes que un orbital 3d
(n+ ℓ = 5). La razón por la que se llena antes el orbital 4s que el 3d, se debe a que la energía de
repulsión entre los electrones situados en orbitales 3d, que están más localizados en el espacio, es
mayor que la energía de repulsión entre electrones situados en orbitales 4s, que están menos
localizados.
Cálculos teóricos, mediante el método de Hartree, analizado en la lección anterior,
confirman que para el átomo de Cr la configuración electrónica [Ar]4s13d5, con 6 electrones
desapareados, es de menor energía que la configuración [Ar]4s23d4, con 4 electrones
desapareados. Este fenómeno es interpretado mediante las denominadas interacciones spinorbital, que se analizarán más adelante, aunque no puede predecirse de forma general, por lo
que deben efectuarse cálculos para resolver la ecuación de Schrödinger. La regla de Hund lo
predice en muchas ocasiones, aunque no en todas. Hay que recalcar, que la configuración
electrónica del Cr [Ar]4s13d5, con solo 4 electrones desapareados, por ejemplo:
2
4
4s1 3d z22 3d1x 2 − y2 3d1xy 3d1xz 3d 0yz , es de mayor energía que la configuración [Ar]4s 3d , con 4
electrones desapareados.
La configuración electrónica de un átomo es una representación basada en la aproximación de
electrones independientes, donde a cada electrón se le asignan 4 números cuánticos, procedentes de las
soluciones del átomo de hidrógeno. Una configuración electrónica no es equivalente a un nivel de
energía, como ocurría en el átomo de hidrógeno. En átomos polielectrónicos la situación energética es
mucho más compleja, ya que la configuración electrónica no tiene en cuenta, ni la repulsión entre
electrones, ni las interacciones entre los momentos angulares orbital y de spin (interacciones spinorbital).
182
Lección 8 Química Física (Curso 2010-11)
MOMENTO ANGULAR EN ÁTOMOS POLIELECTRÓNICOS
JG
El momento angular orbital total de un átomo polielectrónico L , se define como la suma
JG
JG
vectorial de los momentos angulares orbitales individuales de cada electrón L = ∑ i A i . A partir de
esta definición es posible construir los operadores L2 y Lz. Puede demostrarse que estos operadores
conmutan con el Hamiltoniano del átomo polielectrónico, [H,L2] = 0 y [H,Lz] = 0, lo que nos indica
que las observables correspondientes a estos operadores, se conservan, o sea, están cuantizadas.
Figura 8.4
Las propiedades de L2 y Lz, son idénticas a las estudiadas para electrones individuales, es decir
L2ψ = L(L+1)ħ2ψ, y Lzψ = MLħψ, siendo L un número entero mayor o igual que cero (0, 1, 2..), el cual
se representa por una letra mayúscula (S, P, D ...). Además ML, toma valores desde L hasta –L, de
unidad en unidad.
Sin embargo, los operadores ℓi2 y ℓz, individuales de cada electrón (se utiliza letras pequeñas
para no confundirlos con los totales), no conmutan con el operador H, debido a la existencia de los
términos 1/rij de repulsión entre electrones, y por lo tanto, las observables correspondientes no se
conservan, o lo que es lo mismo, no están cuantizadas. Asignar números cuánticos individuales a cada
electrón, es decir, asignar una configuración electrónica al átomo, es una aproximación matemática
(aproximación de electrones independientes), de la que partimos para obtener soluciones más
próximas a las reales. La energía real del átomo no depende de dichos números cuánticos individuales,
sino de los números cuánticos totales L y ML, y como veremos, también S y MS.
Los números cuánticos individuales de cada electrón y por tanto las configuraciones
electrónicas, nos sirven para hacernos una idea mental aproximada de la situación de los electrones en
el átomo, y además, nos permiten determinar de una forma relativamente sencilla los números
cuánticos L y S totales. Vamos a analizar cómo se construyen los números cuánticos totales del átomo:
Supongamos un átomo en el que existen dos electrones, uno con ℓ1 =3, y otro con ℓ2 = 1. En
cada caso, mℓ =0, ±1, .. ±ℓ.
Los valores de ℓ no pueden ser sumados, ya que están relacionados con el módulo de vectores,
183
Lección 8 Química Física (Curso 2010-11)
sin embargo, los valores de mi si pueden ser sumados tal cual, ya que corresponden a la proyección de
dichos vectores sobre un eje común, el eje z. Definiremos ML = m1 + m2, por lo que existirán tantos
valores de ML como combinaciones posibles de m1 y m2. Todos los valores posibles de ML se muestran
en Tabla 8.2.
Tabla 8.2
Los valores de ML posibles pueden combinarse en tres series que varían entre ±4, ±3, y ±2, de
unidad en unidad. Estas tres series nos indican que existen tres valores posibles de L, que son, 4, 3, y
2. Es decir, L toma valores comprendidos entre (ℓ1 + ℓ2) y |ℓ1 - ℓ2|, de unidad en unidad. En general,
JJG
JJG
puede demostrarse que siempre que sumemos dos vectores A 1 y A 2 , cuyos módulos están
JG
cuantizados por las cantidades ħ[ℓ1(ℓ1+1)]1/2 y ħ[ℓ2(ℓ2+1)]1/2, el vector resultante L , tiene también su
módulo cuantizado por la cantidad ħ[L(L+1)]1/2, donde L es un número entero, que puede tomar todos
los valores comprendidos entre (ℓ1 + ℓ2) y |ℓ1 - ℓ2|, de unidad en unidad.
JG
JJG
G
G
La misma regla se cumple si sumamos dos vectores s1 y s 2 , ó A y s . Así, si tenemos dos
electrones con s1 = 1/2 y s2 = 1/2, S toma valores comprendidos entre s1 + s2 y |s1 - s2|, de unidad en
unidad, es decir, S = 0 y 1.
Si en el átomo existe otro electrón, los números cuánticos ℓ3 y s3, del tercer electrón, se
adicionan siguiendo las mismas reglas, al resultado de adicionar los dos anteriores. Veamos un
ejemplo con el spin. Así, el resultado de adicionar el spin de dos electrones es; S1,2 = 1 y 0. Este
resultado se adiciona a s3 = 1/2, de forma que S toma valores comprendidos desde S12 + s3 hasta |S12 s3|. Como existen dos valores de S12, tendremos dos opciones: S = 3/2 y 1/2 (1+1/2....1-1/2), y S= 1/2
(1/2+0). En la práctica solo hay dos valores , S = 3/2 y 1/2(repetido).
Como vimos para el átomo de hidrógeno, los momentos angulares de spin y orbital llevan
asociados momento magnéticos que interaccionan entre sí. Estas interacciones afectan notablemente a
la estructura energética del átomo.
184
Lección 8 Química Física (Curso 2010-11)
INTERACCIONES SPIN-ORBITAL
Las interacciones entre los momentos magnéticos, orbital (L) y de spin (S) son muy
complejas, y dependen del tamaño del átomo. Así para átomos ligeros (aproximadamente la mitad de
la tabla periódica), dominan las interacciones denominadas de spin-orbital o de Russell-Saunders, que
son las únicas que veremos aquí. Sin embargo, para átomos pesados, dominan otros tipos de
interacciones denominadas acoplamientos j-j. Los datos experimentales indican que la energía de los
electrones en átomos polielectrónicos ligeros, depende del momento angular total del átomo
G JG G
J = L+S
(8.32)
El módulo de J, esta cuantizado mediante la relación ya conocida
G
J = = J ( J + 1)
(8.33)
donde J es un número cuántico entero, o semientero, que toma valores positivos o cero, comprendidos
entre L + S, y |L – S|, de unidad en unidad. La proyección del vector J sobre un eje, esta cuantizada
mediante otro número cuántico, MJ, tal que MJ = ML + MS, de forma que MJ toma valores
comprendidos entre J y –J, de unidad en unidad. Si L≥S, el número de valores de J (L+S, L+S-1....LS), es 2S+1. A esta magnitud se le denomina multiplicidad, y representa el número de valores de J,
para unos valores dados de L y S. Cuando S > L, el valor 2S+1, no representa el número de valores de
J.
La energía de cada estado depende de los tres números cuánticos L, S y J, así como del
número cuántico principal n, y por esta razón se construyen los denominados términos
espectroscópicos.
n 2S+1 L J
⎧0 1 2 3 4 5 6 "
L=⎨
⎩S P D F G H I "
(8.34)
Como ejemplo, supongamos una configuración electrónica np1 n’p1, donde n ≠ n’, por lo que
los electrones poseen ya un número cuántico diferente. A estos electrones, se les denominan no
equivalentes. Para nuestros dos electrones, ℓ1 = 1, ℓ2 = 1, s1 =1/2 y s2 = 1/2. Por lo tanto, L = (ℓ1 + ℓ2)
... |ℓ1 - ℓ2| = 2, 1, 0, y S = 1,0. Luego, existirán términos correspondientes a todas las posibles
3
1
3
1
3
1
combinaciones de estos números cuánticos: D, D, P, P, S y S. Los valores de J están
3
1
3
1
3
1
comprendidos entre L+S .. |L-S|, luego D3,2,1, D2, P2,1,0, P1, S1 y S0. De una forma cualitativa, la
energía de los términos espectroscópicos, para una configuración electrónica dada, puede clasificarse
según las denominadas reglas de Hund. Estas son:
1. La energía del estado es menor cuanto mayor sea S.
2. A igualdad de S, la energía es menor cuanto mayor sea L.
3. Si la configuración electrónica es menor de semi-llena, la energía será mínima cuanto
menor sea J. Si es igual o mayor que semi-llena, la energía será mínima cuanto mayor sea J.
185
Lección 8 Química Física (Curso 2010-11)
En la Figura 8.5, se muestra el diagrama cualitativo de energía de los 10 términos
espectroscópicos, o 10 niveles de energía que aparecen para la anterior configuración.
Figura 8.5
Cada uno de los 10 niveles de configuración esta degenerado en MJ, existiendo 2J+1 valores
para cada término. El número de valores de MJ, se muestra asimismo en la columna de la derecha de la
Figura 8.5. Es decir, existen 10 niveles de energía y 36 estados.
A cada una de las combinaciones posibles de los números cuánticos individuales de los
electrones, se le denomina microestado. Para una configuración p1, existen 6 microestados, es decir, 6
formas diferentes de asignar números cuánticos al electrón (3 valore de mℓ y dos de ms). Como nuestra
configuración es np1n’p1, (electrones no equivalentes), y por lo tanto los electrones ya tienen un
número cuántico diferente, el número de microestados será 6×6 = 36. El número de microestados ha
de coincidir con el número de estados totales obtenidos a partir de los términos espectroscópicos. En
realidad, utilizar los números cuánticos individuales, ℓ, m, s, y ms, es equivalente a utilizar los
números L, S, J y MJ, solo modificamos la forma de combinarlos, aunque conviene expresar los
estados en función de los números cuánticos totales ya que la energía depende de ellos. En la Tabla
8.3, se muestran los términos correspondientes a otras configuraciones de electrones no equivalentes.
Tabla 8.3
Supongamos ahora, que la configuración es np2. A estos electrones se les denomina
equivalentes, ya que poseen dos números cuánticos iguales (n y ℓ). Bajo estas condiciones, es
necesario tener en cuenta el principio de exclusión de Pauli. El número de microestados para
186
Lección 8 Química Física (Curso 2010-11)
electrones equivalentes puede determinarse mediante la relación:
Microestados =
m!
6!
=
= 15
( m − n )!n! 4!2!
(8.35)
donde m es el número de electrones que caben en el orbital (6 en nuestro caso) y n, el número de
electrones que existen (2 en nuestro caso). Luego una configuración p2, da lugar a 15 microestados.
Los 15 microestados, o formas de asignar números cuánticos, de la configuración p2 se
muestran en la Tabla 8.4. Con estos microestados puede determinarse todos los posibles valores de ML
y MS, sumando directamente los valores mℓ y ms individuales de los electrones (ver columnas 4 y 5 de
la tabla). Una vez que se tienen los valores de ML y MS, se agrupan en diferentes series que nos
permitan calcular L y S, dado que dichos números cuánticos varían entre +L y -L (ML), y entre +S y –
S (MS), de unidad en unidad.
mR=1 0
-1
¼¿
¼
¿
¼
¼
¿
¼
¼
¿
¼
¿
¿
¿
¿
¼
¿
¼
¼¿
ML =3mR
MS =3ms
2
0
1
0
0
0
1
1
0
1
1
-1
0
-1
1
0
0
0
0
0
¼
¿
-1
0
¼
¼
-1
1
¿
¼
-1
0
¿
¿
-1
-1
¼¿
-2
0
Tabla 8.4
Así, existe una serie de 5 microestados (sombreado oscuro en la tabla anterior), para los que
MS = 0 y ML = 0, ±1, ±2, por lo que para este conjunto de microestados S = 0 y L = 2. Por lo tanto J =
2. Luego a estos 5 microestados le corresponde el término 1D2.
Existen además, un conjunto de 9 microestados, que han sido señalados por un sombreado
claro. Estos 9 microestados pueden clasificarse en tres grupos a su vez. En uno de ellos, ML = 0, ±1, y
MS =1 (triple raya entre las columnas 4 y 5 de la tabla). En otro ML = 0, ±1, y MS = 0 (doble raya en la
187
Lección 8 Química Física (Curso 2010-11)
tabla), y en el último ML =0, ±1, y MS = -1 (raya simple en la tabla). Es decir, en este conjunto de 9
microestados, ML = 0, ±1, y MS = 0, ±1, luego, L = 1 y S = 1, por lo que J = 2,1,0, y por lo tanto,
existen tres términos espectroscópicos 3P2,1,0.
Por último, queda un microestado para el que MS = 0 y ML = 0, luego S = 0 y L = 0, de forma
que J = 0, a lo que le corresponde el término 1S0.
Aplicando las reglas de Hund, podemos ordenar los términos por orden creciente de energía,
de una forma cualitativa, tal como se muestra en la Figura 8.6.
Figura 8.6
Cuando se compara este diagrama de energía con el descrito anteriormente para electrones no
equivalentes (Figura 8.5), se observa que aparecen menos términos, lo que se debe al principio de
exclusión de Pauli. La configuración electrónica p2 conduce por lo tanto a 5 niveles de energía, siendo
3
el término fundamental, el P0.
En la Tabla 8.5, se muestran los términos espectroscópicos correspondientes a otras
configuraciones de electrones equivalentes.
Tabla 8.5
El método descrito para calcular los términos espectroscópicos es enormemente engorroso y
en la práctica no se utiliza, piénsese que para una configuración f3, existen 364 microestados. En el
apéndice 8.1, se describe un procedimiento empírico para construir los términos espectroscópicos de
cualquier configuración electrónica.
Existen dos casos particulares que merecen ser mencionados:
188
Lección 8 Química Física (Curso 2010-11)
En primer lugar, una capa completa no contribuye a los momentos angulares orbital y de spin,
ya que para ella L = 0 y S = 0. Por esta razón, los electrones internos, correspondientes a capas llenas,
no participan en el término espectroscópico. Así, por ejemplo, para construir los términos
espectoscópicos de un átomo con una configuración electrónica 1s22s2p63s1, solo es necesario
considerar sus capas semillenas, es decir, 3s1, donde, S = 1/2, L = 0, y J = 1/2, siendo su término
2
espectroscópico, por tanto: S1/2.
En segundo lugar, si bien es complejo calcular todos los términos espectroscópicos de una
configuración electrónica dada, es sencillo, sin embargo, calcular el término espectroscópico
fundamental para cualquier configuración electrónica. Nos basta con aplicar las reglas de Hund, y
buscar los microestados que la cumplan; en primer lugar con (MS)maximo = S, y a continuación con
(ML)máximo = L. Veamos por ejemplo cómo aplicar esto para una configuración p3. La primera regla de
Hund nos dice, que el estado es de menor energía cuanto mayor es S. Como MS varía entre ± S de
unidad en unidad, debemos buscar, para dicha configuración el valor máximo posible MS. El valor
máximo de Ms lo tendríamos cuando los tres electrones se colocan desapareados en el orbital. Esto se
ilustras en la Figura 8.7-a, donde se representa un microestado con MS = 3/2. La forma de representar
los microestados, es dibujar tantas casillas como valores de mℓ existen, en nuestro caso, 1, 0 y -1, y
dentro de cada casilla, dibujar una flecha hacia arriba, por cada electrón con ms = +1/2, o una flecha
hacia abajo, por cada electrón con ms = -1/2. Pero con MS = 3/2, solo existe un microestado, el
dibujado en la Figura, para el cual ML =0, luego S=3/2 y L=0, por lo tanto J=3/2. Luego el término
fundamental es 4S3/2.
1
a)
¼
0
¼
-1
b)
2
¼
¼
1
0
-1
¼
¼
¼
-2
Figura 8.7
4
Para una configuración d , el valor máximo posible de MS = 2 (ver Figura 8.7-b). Para
este valor de MS el valor máximo de ML permitido es ML=2, luego S=2 y L=2, como la capa esta
menos de semillena, J= 0, luego el término fundamental es 5D0.
189
Lección 8 Química Física (Curso 2010-11)
ESTRUCTURA ENERGÉTICA Y ESPECTROS DE ÁTOMOS POLIELECTRÓNICOS
Los espectros de átomos polielectrónicos solo pueden ser interpretados si se conoce cuál es la
estructura energética del átomo, es decir, cuáles son sus niveles de energía. Para determinar los niveles
de energía de un átomo, aunque sea solo de forma cualitativa, necesitamos determinar los términos
espectroscópicos para todas sus posibles configuraciones electrónicas.
Como ejemplo analicemos el átomo de He, el cual en su estado fundamental posee una
configuración 1s2, luego le corresponde un término espectroscópico 11S0. La energía de los diferentes
términos del átomo se ilustra en la Figura 8.8.
Figura 8.8
La primera configuración electrónica excitada del He es 1s1, 2s1, o en general, 1s1ns1, con n >
1. Para todos estos casos ℓ1 =0 y ℓ2 =0, luego L=0. Al existir dos electrones no equivalentes, S puede
tomar dos valore S = 0, 1, luego J = 0, 1, por lo que tenemos términos espectroscópicos n1S0 y n3S1. Al
helio con spin cero se le denomina para-helio, mientras que al que tiene spin 1, orto-helio.
La siguiente configuración electrónica excitada del He es 1s12p1, o también en general, 1s1
np1, donde n > 1. Para todos estos casos ℓ1 =0 y ℓ2 =1, luego L=1. Al existir dos electrones no
equivalentes S puede tomar dos valore S = 0,1, luego para S= 0, J =1, por lo que el término
espectroscópico es n1P1. Para S = 1, J = 2, 1, 0, luego existen tres términos , n3P2,1,0.
De la misma forma, para una configuración electrónica 1s1nd1, los términos espectroscópicos
sería n1D2 y n3D3,2,1. Para una configuración 1s1nf1, los términos espectroscópicos serían n1F3 y
n3F4,3,2, etc. La energía de estos estados se muestra en la Figura 8.8. Asimismo, en la Figura 8.2, si
190
Lección 8 Química Física (Curso 2010-11)
indica la energía de los primeros estados energéticos del átomo, relacionándose la nomenclatura
utilizada al comienzo de la lección, con la basada en los términos espectroscópicos. Cuando al átomo
de He se le comunica una energía de 24.5 e.v. = 198305 cm-1, tiene lugar el primer potencial de
ionización del átomo.
No todos los saltos posibles están permitidos mediante absorción y emisión de radiación. Las
reglas de selección para átomos polielectrónicos son las siguientes:
*Para el electrón que salta de una configuración electrónica a otra Δℓ = ±1.
* Para el conjunto de los números cuánticos, ΔS = 0, ΔL = 0, ±1, y ΔJ = 0, ±1, salvo el salto
de J = 0, a J = 0, que está prohibido.
Según estas reglas, en el espectro de absorción solo aparecen los tránsitos desde 11S0 → n1P1.
Sin embargo, los espectros de emisión son mucho más complejos, ya que el retorno del electrón al
estado fundamental no tiene por qué ser en un solo paso, sino en cascada. En la Figura 8.8, se
muestran algunos de los posibles saltos espectroscópicos del espectro de emisión.
Veamos un ejemplo más complejo, como es el del átomo de carbono. En la Figura 8.9, se
ilustra el diagrama de energía de algunos de sus estados.
Figura 8.9
La configuración electrónica del estado fundamental del carbono es 2s2p2, luego, para una
configuración p2, los términos son 3P, 1D y 1S. Nosotros podemos predecir cualitativamente el orden
pero no la energía exacta sin efectuar cálculos. El carbono en su estado fundamental se sitúa en un
término 3P (2 electrones desapareados).
Una primera configuración electrónica excitada es, 2s2p13s1, es decir p1s1, para la que tenemos
191
Lección 8 Química Física (Curso 2010-11)
términos, 1P y 3P. La siguiente configuración electrónica excitada es 2s2p13p1, es decir p1p1 (no
equivalentes), para la que tenemos términos S, P y D con multiplicidad 1 y 3.
Sin embargo, experimentalmente, también es posible la configuración 2s1p3. Esta es una
configuración electrónica denominada mixta, con electrones equivalentes, los p3 y no equivalentes, s1.
Los términos de esta configuración no aparecen en la tabla 8.3, sin embargo, son fáciles de calcular.
Los términos de la configuración p3 si aparecen en dicha tabla, siendo 4S (S=3/2, L=0), 2D (S = 1/2,
L=2) y 2P (S= ½ y L=1). Estos son los números cuánticos correspondientes a los 3 electrones p
equivalentes. El del cuarto electrón (2s1) se adiciona a los anteriores sin ninguna restricción, ya que es
no equivalente, como para este electrón ℓ4 = 0, el L total coincide con el de los electrones p3 y el s4 =
1/2, por lo que habría que adicionarlo a los anteriores, siguiendo las reglas habituales. Así, para L = 0,
S = {2,1}, para L = 2, S = {1,0} y para L=1, S = {1,0}, lo que conduce a términos 5S, 3S, 3D, 1D, 3P y
1
P.
Como puede observarse de la Figura 8.9, las reglas empíricas de Hund no son
infalibles, y, por ejemplo, para la configuración 2s1p3 el término 1D, es de menor energía que el
3
S, o para la 2s2p13p1, el orden de los términos es 1P, 3D, 3S, 3P, 1D y 1S. A medida que el peso atómico
del átomo aumenta, y sobre todo para configuraciones excitadas, la reglas de Hund son cada vez
menos fiables. Además, el orden relativo de los términos de una configuración con respecto a otra es
imposible de predecir sin efectuar cálculos numéricos.
Con el fin de interpretar los espectros de átomos polielectronicos se recurre a dos métodos
experimentales. Uno de ellos consiste en la realización de espectros en presencia de campos
magnéticos. En este caso, la energía se hace función de MJ, de forma semejante a como ocurría con el
átomo de hidrógeno, observándose el desdoblamiento de ciertas líneas espectrales (efecto Zeeman). La
energía de interacción entre un campo magnético externo, B, y el momento magnético total del átomo
viene dada por
JG
E int eraccion = gμ B M J B
(8.36)
donde μB, es el magnetón de Bohr, y g es una relación entre los números cuánticos L, S y J, dada por:
3J(J + 1) + S(S + 1) − L(L + 1)
g=
(8.37)
2J(J + 1)
La deducción teórica de esta expresión, se realiza en el Apéndice 8.2. Otro método al que se
recurre para interpretar espectros, es la realización de estos en presencia de campos eléctricos. En
presencia de un campo eléctrico, la energía de los estados se hace función de |MJ| (efecto Stark).
192
Lección 8 Química Física (Curso 2010-11)
APÉNDICE 8.1: CONSTRUCCIÓN DE TÉRMINOS ESPECTROSCÓPICOS.
Existe un método empírico sencillo para determinar los términos espectroscópicos de una
configuración de electrones equivalentes dada. Supongamos la configuración np2, y construyamos
mediante tablas todos los valores posibles de ML y MS. Estos se muestran en la Figura 8.10.
ms1 ms2 1/2
-1/2
1/2
1
0
1/2
0
-1
m1
m2
MS
ML
1
0
-1
1
2
1
0
0
1
0
-1
-1
0
-1
-2
Figura 8.10
Existen 4 valores de MS, y 9 de ML, de forma que 4×9 = 36 microestados, como ya sabíamos.
Pero de estos 36 microestados, solo son posibles 15, a consecuencia del principio de exclusión de
Pauli. Supongamos que el spin total es S = 1 (MS = 1, 0, -1)(↿↾). Cuando esto ocurre, los dos
electrones poseen 3 números cuánticos iguales, n, ℓ y ms, por lo que los electrones deben tener el
número cuántico, mℓ diferente, por lo que en la tabla de valores de ML, debemos eliminar los términos
de la diagonal, que se construyen con idénticos valores de mℓ para los dos electrones. Esto se ilustra en
la Figura 8.11, donde se muestra la tabla de valores de ML, para S = 1, en la que los valores de la
diagonal han sido tachados.
S= 1
S =0
1
0
-1
m1
1
2
1
0
0
1
0
-1
0
-1
m1
m2
m2
1
0
-1
1
2
1
0
-1
0
1
0
-1
-2
-1
0
-1
-2
Figura 8.11
Tras eliminar estos valores, nos queda que ML toma valores de 1 0 y -1, por lo que L=1, y
como S=1, tendremos términos; 3P2, 3P1, 3P0. Solo se toma un lado de la diagonal, ya que de lo
contrario se discrimina entre electrones. Estos 3 términos corresponden a 9 microestados, 3 valores de
193
Lección 8 Química Física (Curso 2010-11)
ML ×3 de MS.
Si ahora suponemos S = 0 (cuadro de la derecha en la Figura 8.11), en este caso, los electrones
ya tienen un número cuántico diferente (ms), por lo que no existe ninguna restricción en cuanto a los
valores de ML. Si bien, se eliminan de la tabla los valores ya utilizados (regla empírica), es decir, 1, 0
y -1 (valores tachados). Por lo tanto ML = {2, 1, 0, -1, -2} y {0}, por lo que L = 2 y 0, por lo que
tenemos términos 1D2 y 1S0. Estos términos corresponden a 6 microestados, que con los 9 de antes son
15.
Veamos otro ejemplo, supongamos una configuración nd1n’d1 (electrones no equivalentes
n≠n’). Como ℓ1 = 2 y ℓ2 = 2, L = 4, 3, 2, 1, 0, y S = 1, 0. En este caso, todas las combinaciones son
posibles, por lo que existirían términos 1S, 1P, 1D, 1F, 1G, 3S, 3P, 3D, 3F, 3G, con los correspondientes
valores de J que no haremos.
Supongamos ahora que los electrones son equivalentes, (n = n’) (nd2). Como en el caso
anterior el spin total es 1 o 0. Se construye la tabla de valores de ML (ver Figura 8.12). Si S = 1, hay
que eliminar los valores de la diagonal (ya que en caso contrario los electrones tendrían su 4 números
cuánticos iguales), por lo que, los valores de ML que nos quedan (en blanco en la Figura), serían; ML =
{3,2,1,0,-1,-2,-3} y {1,0,-1}, luego L = 3 y 1. Lo que implica términos 3F y 3P. Por otra parte cuando S
= 0, los electrones ya tienen un número cuántico diferente (ms), por lo que no existen restricciones, en
este caso L = {4,3,2,1,0}, pero hay que eliminar los valores utilizados con S = 1, por lo que L = 4,2,0,
o sea, 1S, 1D y 1G.
S =1
m1 m2
2
1
0
-1
-2
2
4
3
2
1
0
1
3
2
1
0
-1
0
2
1
0
-1
-2
-1
1
0
-1
-2
-3
-2
0
-1
-2
-3
-4
Figura 8.12
Estas reglas se pueden utilizar con más electrones, adicionando primero dos electrones, al
resultado el tercero, y así sucesivamente.
194
Lección 8 Química Física (Curso 2010-11)
APÉNDICE 8.2: EFECTO ZEEMAN
Con el fin de interpretar los espectros de átomos polielectronicos, se recurre a diferentes
métodos experimentales. Uno de ellos es la realización de espectros en presencia de campos
magnéticos (efecto Zeeman). En estos casos, la energía de los estados se hace función de MJ, de forma
semejante a como ocurría con el átomo de hidrógeno, observándose el desdoblamiento de ciertas
lineas espectrales. En la Figura 8.13, se muestra un equema donde se representan algunos de los
vectores definidos a continuación.
Figura 8.13
Los momentos magnéticos orbital y de spin tienen la forma
JJG
μ JG
μL = − B L
=
JJG
μ G
μS = −2 B S
=
(8.38)
donde μB = eℏ/2mc, es el magneton de Bohr. El momento magnético total será:
JJG
G
μ JG
μ T = − B L + 2S
=
(
)
(8.39)
El vector J (momento angular total), se definió como
G JG G
J = L+S
(8.40)
Por lo que los vectores J y μT no están en la misma dirección, como se observa en la Figura
8.13. Supongamos que aplicamos un campo magnético B. La energía de interacción entre dicho campo
y el momento magnético total del átomo será:
JJG JG
G
μ JG JG
E = μ T ⋅ B = − B B L + 2S
=
(
)
(8.41)
Esta interacción interesa expresarla en función de J y MJ, y no de μT directamente. Por ello, se
introduce el siguiente cambio:
195
Lección 8 Química Física (Curso 2010-11)
(
)
G2 G G
G G G G
G G
J + J ⋅S G
J ⋅ J + J ⋅S G
JG
G G G G G J⋅J
L + 2S = J + S = J + S G G =
J=
J
G2
G2
J⋅J
J
J
(
(
)
Además, si se tiene en cuenta que
JG JG G G
L⋅L = J −S
(
)
2
)
G G G G G G
= J ⋅ J + S ⋅ S − 2J ⋅ S
(8.42)
(8.43)
Por lo que
G 2 G 2 JG 2
G G J +S −L
J ⋅S =
2
(8.44)
Luego
(
)
G 2 G 2 JG 2
⎛ G 2 1 G 2 1 G 2 1 JG 2 ⎞
JG
G ⎜⎝ J + 2 J + 2 S − 2 L ⎟⎠ G 3 J + S − L G
G
L + 2S =
J
J
gJ
=
=
G2
G2
J
2J
(8.45)
Donde, teniendo en cuenta la relación entre los módulos al cuadrado de cada vector, y
los números cuánticos correspondientes J, L y S, es posible expresar el factor numérico que
multiplica al vector J, como:
G 2 G 2 JG 2
3J + S − L
3= 2 J(J + 1) + = 2S(S + 1) − = 2 L(L + 1)
g=
=
=
G2
2= 2 J(J + 1)
2J
=
(8.46)
3J(J + 1) + S(S + 1) − L(L + 1)
2J(J + 1)
Al factor g, se le denomina factor g de landé, y su valor depende únicamente de los tres
números cuánticos L, S y J. Por lo tanto, la energía de interacción entre el campo magnético externo y
el momento magnético del átomo será:
G
μ B JG JG
μ JG G
μ JG G
B L + 2S = −g B B ⋅ J = −g B B ⋅ J cos(θ) =
=
=
=
JG
μ B JG G
μ B JG G M J =
=g
B ⋅ J cos(π − θ) = g
B ⋅ J G = gμ B M J B
=
=
J
E=−
(
)
(8.47)
Es decir, la acción del campo magnético rompe la degeneración en MJ, apareciendo tantos
niveles de energía como valores de MJ existen. Por lo tanto, cuando se realiza un espectro en presencia
de un campo magnético, se observa el desdoblamiento de las líneas espectrales, lo cual se conoce
como efecto Zeeman. En la Figura 8.14, se muestra un ejemplo correspondiente a la transición entre
los estados 2S1/2 → 2P1/2. Esta transición, que aparece como una banda en el espectro, se desdobla en 4
bandas en presencia de un campo magnético externo. Una representación esquemática de dicho
desdoblamiento, se muestra también en la Figura 8.14.
196
Lección 8 Química Física (Curso 2010-11)
Figura 8.14
197
Lección 8 Química Física (Curso 2010-11)
CUESTIONES
1) Justificar por qué en sistemas polielectrónicos, las funciones de onda deben ser antisimétricas.
2) En base al principio de antisimetría, explicar porqué es imposible que un átomo posea una configuración
electrónica ns3.
3) Definir, lo más brevemente posible, que se entiende por configuración electrónica de un átomo, e indicar
porqué, en general, estas no coinciden con los niveles de energía de los átomos.
4) Bajo la aproximación de electrones independientes, la función de onda espacial de cierto estado del átomo de
He puede escribirse como; ψ = N[φ1s(1)φ2s(2) + φ1s(2)φ2s(1)]. Normalizar la función, sabiendo que los orbitales
φ1s y φ2s están normalizados, y que dτ = dτ1dτ2. Escribir la función spin-orbital completa, e indicar el término
espectroscópico de dicho estado.
5) Según la aproximación de electrones independientes las configuraciones 1s12s1 y 1s12p1 son degeneradas.
)Cuantos niveles de energía corresponden a dichas configuraciones y como se denominan?. )A que fenómenos
físicos debe achacarse el hecho de que las configuraciones electrónicas 1s12s1 y 1s12p1 no correspondan a un
solo nivel de energía?
6) En la aproximación de electrones independientes, la parte espacial de los estados electrónicos del átomo de He
tienen la forma: ψ = N[φα(1)φβ(2) ± φα(2)φβ(1)]. Para dos casos genéricos en los que α = β y α ≠ β, construye
todos los spin-orbitales que pueden existir, e indica cual es el spin en cada caso.
7) Explica lo más brevemente posible porqué deben utilizarse los determinantes de Slater para construir las
funciones de onda de los átomos poli-electrónicos.
8) Indicar si las siguientes funciones de onda correspondientes a diferentes configuraciones del átomo de He, son
correctas o no. En caso de que no lo sean indicar porqué, y en caso de que lo sean indicar el spin
correspondiente.
I) ψ = N ⎡⎣φ1s (1) φ1s ( 2 ) − φ1s ( 2 ) φ1s (1) ⎤⎦ σ + (1) σ+ ( 2 )
II) ψ = N ⎡⎣φ1s (1) φ2s ( 2 ) − φ1s ( 2 ) φ2s (1) ⎤⎦ ⎡⎣σ + (1) σ − ( 2 ) + σ + ( 2 ) σ − (1) ⎤⎦
III) ψ = Nφ1s (1) φ2s ( 2 ) ⎣⎡σ + (1) σ − ( 2 ) − σ + ( 2 ) σ − (1) ⎦⎤
IV) ψ = N ⎡⎣φ1s (1) φ2s ( 2 ) + φ1s ( 2 ) φ2s (1) ⎤⎦ ⎡⎣σ+ (1) σ − ( 2 ) − σ + ( 2 ) σ − (1) ⎤⎦
V) ψ = Nφ1s (1) φ1s ( 2 ) ⎡⎣σ + (1) σ − ( 2 ) + σ + ( 2 ) σ− (1) ⎤⎦
PROBLEMAS
1) a) Construir la función de onda antisimétrica de orden cero del boro, cuya configuración electrónica es,
1s22s2p1. Indicar si la energía que se obtiene al aplicar la teoría de variaciones a la función anterior, es mayor,
menor o igual, que la energía experimental del átomo.
b) En unidades atómicas la energía del electrón en un átomo hidrogenoideo es En = -Z2 /2n2, donde Z es
la carga nuclear. Determinar la energía de los electrones del átomo de boro, según la aproximación de electrones
independientes, e indicar si la energía obtenida es mayor, menor o igual, que la energía experimental del átomo.
Utilizar como energía experimental del átomo, la que se obtiene según el método aproximado de Slater.
2) Sea un sistema cuántico, en el cual existen infinitos estados no degenerados con energía En =n2h2/8ma2, donde
n = 1, 2, 3, ... . Supóngase además, que en el sistema existen tres partículas idénticas no interaccionantes.
Determinar la energía mínima del sistema cuando las partículas son Fermiones y cuando son Bosones.
3) Deducir el término espectroscópico fundamental de las siguientes configuraciones electrónicas.
d3
f3,
f9,
s1d2,
p2d2,
p5,
4) Determinar la configuración electrónica que corresponde a los términos atómicos fundamentales: 3F2, 4S3/2,
6
S5/2, 7F0.
198
Lección 8 Química Física (Curso 2010-11)
5) Explicar porqué son erróneos los siguientes símbolos de los niveles de un átomo.
asimismo, qué valores de J, pueden tomar los siguientes términos 1S, 2P, 3P, 3D y 4D.
4
S1, 2D7/2 y 0P1. Indicar,
6) Todos los términos espectroscópicos de cierta configuración electrónica son: 2P1/2, 2P3/2, 2D3/2, 2D5/2, 4S3/2. a)
Determinar de qué configuración se trata, y cuál es el término fundamental. b) Ordenar los términos por orden
creciente de energía e indicar que transiciones están permitidas desde el término fundamental a los restantes.
7) En la Figura 8.15, se muestran algunas de las transiciones electrónicas observadas para el átomo de oxígeno.
3
S
8
6
1
S
4
2
1
D
3
P
Figura 8.15
a) Indicar que términos, de los representados, pertenecen a la configuración electrónica fundamental de dicho
átomo.
b) La primera configuración electrónica excitada del átomo de O es 1s22s2p33s1. Determinar el término
espectroscópico fundamental de esta configuración e indicar si el término 3S, pertenece o no a dicha
configuración.
c) Indicar las transiciones permitidas, mediante absorción de radiación, entre los estados representados en la
figura.
d) Las emisiones de radiación desde 1D ÷ 3P (λ = 630 nm, rojo), y 1S ÷ 1D (λ = 557.7 nm, verde), son
observadas en la luz que forman las Auroras Boreal y Austral. )Contradice esta observación las conclusiones del
apartado anterior?. Razonar en cualquier caso la respuesta.
8) Indica el número de microestados, los términos espectroscópicos, y el término fundamental, correspondientes
a una configuración p1d1.
9) Normalizar la siguiente funciones y demostrar que son ortogonales entre si.
ψ s = N ⎡⎣φ1s (1) φ2s ( 2 ) + φ1s ( 2 ) φ2s (1) ⎤⎦
ψ a = N ⎡⎣φ1s (1) φ2s ( 2 ) − φ1s ( 2 ) φ2s (1) ⎤⎦
199