Antena Yagi

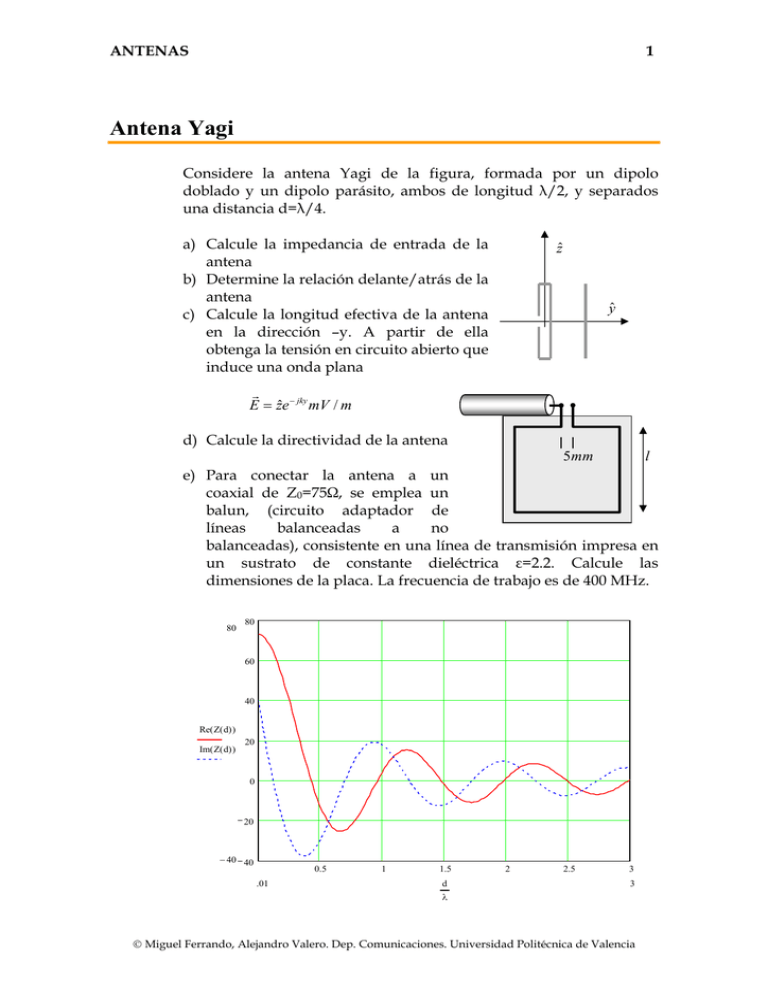
ANTENAS
1
Antena Yagi
Considere la antena Yagi de la figura, formada por un dipolo
doblado y un dipolo parásito, ambos de longitud λ/2, y separados
una distancia d=λ/4.
a) Calcule la impedancia de entrada de la
antena
b) Determine la relación delante/atrás de la
antena
c) Calcule la longitud efectiva de la antena
en la dirección –y. A partir de ella
obtenga la tensión en circuito abierto que
induce una onda plana
ẑ
ŷ
G
ˆ − jky mV / m
E = ze
d) Calcule la directividad de la antena
5mm
l
e) Para conectar la antena a un
coaxial de Z0=75Ω, se emplea un
balun, (circuito adaptador de
líneas
balanceadas
a
no
balanceadas), consistente en una línea de transmisión impresa en
un sustrato de constante dieléctrica ε=2.2. Calcule las
dimensiones de la placa. La frecuencia de trabajo es de 400 MHz.
80
80
60
40
Re( Z( d) )
Im( Z( d) )
20
0
20
− 40 40
0.5
.01
1
1.5
d
2
2.5
3
3
λ
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
Solución
Impedancia de entrada
La impedancia de una antena yagi se puede calcular a partir de su
equivalente de radiación
V
= z11 I1 + z12 I 2 + z13 I 3
2
V
= z21 I1 + z22 I 2 + z23 I 3
2
0 = z31 I1 + z32 I 2 + z33 I 3
Teniendo en cuenta las simetrías del problema
z11 = z22 = z12 = z21 = z33 = 73 + j 42
z23 = z32 = z31 = z13 = 41 − j 28
Se obtiene la fórmula para la impedancia de entrada
⎛
z2 ⎞
Z in = 4 ⎜ z11 − 13 ⎟ = 309 + j 284Ω
z33 ⎠
⎝
Campos radiados
El dipolo doblado equivale desde el punto de vista de radiación a un
dipolo simple con corriente doble
0 = z31 I1 + z32 I1 + z33 I 3 = 2 z31 I1 + z33 I 3
I 3 = −2
z31
I1 = −2 ( −0.251 + 0.532 j ) I1
z33
El vector de radiación de la antena es
G G ⎛
G ⎛ z jk d ⎞
z jk d ⎞
N = N 0 ⎜ 2 − 2 13 e y ⎟ = 2 N 0 ⎜1 − 13 e y ⎟
z33
⎝
⎠
⎝ z33
⎠
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
El diagrama en dicho plano es
90
120
1.552
60
150
FA( φ )
30
180
0
0
0.5
1
210
0.41
1.5
330
240
300
270
φ
Se observa que el dipolo parásito actúa como reflector. Para calcular
la relación delante-atrás es suficiente con particularizar los valores
del factor de interferencia en las direcciones y, -y.
En la dirección –y, el valor es 1.553, en la dirección y es 0.531. La
relación en dB es 9.32 dB
Longitud efectiva
Calculando la longitud efectiva en emisión
G
G jkrˆ⋅rG '
z jk d ⎞
1
1 G ⎛
'
le =
Je
dv
N 0 ⎜ 2 − 2 13 e y ⎟
=
∫
I ( 0)
I1
z33
⎝
⎠
z jk d ⎞ 2λ ⎛
z13 ⎞ 2λ
λ⎛
1.55
le = ⎜ 2 − 2 13 e y ⎟ =
⎜1 + j
⎟=
z33
z33 ⎠ π
π⎝
⎠ π ⎝
La tensión en circuito abierto es
Vca = − Ei le =
2λ
π
1.55 mv
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Directividad
4π r 2 ( Emax )
P
= 3.75 → 5.7dB
D = max = 2
Wt
I1 Re ( Z in )η
4π r 2
2
Balun
Se trata de un balun simetrizador, cuyo circuito equivalente es una
línea de λe/2 de longitud. Hay que tener en cuenta el valor de la
constante dieléctrica de la placa del circuito impreso.
4l − d =
λ
λe
2
l = 2 2.2
4
+d
= 7.57cm
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia