Teorema de Redes

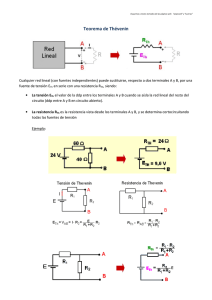
Teorema de Redes
M en C Alejandro Pérez López
México D.F. 27 de enero de 2009
Resumen
La existencia de modelos matemáticos que describen los circuitos equivalente
de sistema eléctricos complejos, para facilitar su análisis y de los comportamientos
de los elementos pasivos y activos que componen un circuito bajo el estudio de la
frecuencia compleja.
1
Índice
1. Introducción
3
2. Teorema de Thevenin
2.1. Voltaje de Thevenin . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.2. Impedancia de Thevenin . . . . . . . . . . . . . . . . . . . . . . . . . .
2.3. Circuito equivalente Thevenin . . . . . . . . . . . . . . . . . . . . . . .
4
4
5
6
3. Teorema de Norton
3.1. Corriente de Norton . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2. Impedancia de Norton . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.3. Circuito equivalente Norton . . . . . . . . . . . . . . . . . . . . . . . .
8
8
9
10
4. Conclusiones
11
2
1.
Introducción
Nos interesa aclarar con detalle aquellas referencias que pueden confundir el análisis
eléctrico substrayendo el interés por su conocimiento. Estas realidades del análisis de
circuitos abundan en nuestras explicaciones y forman parte prominente del curso impartido en la academia de circuitos de ICE, convirtiendo lo que deberı́a ser una motivación
para el aprendizaje de la teoremas eléctricos.
Para calcular la Z o Y de una estructura activa la deberemos pacificar retirando las
fuentes de voltaje y en su lugar se colcoara un corto circuito. de igual manera para las
fuentes de corriente se retira y se deja en su lugar circuito abierto de ahı́ la estructura
se analiza en el estado que queda siendo el calculo de Z y Y como las estructuas pasivas.
Cuando la esctructiura se encuentra contenida dentro de una caja negra y a su vez
contiene fuentes de voltaje y/o de corriente se le denomina estructura activa. Para calcularle la impedancia o admitanciainterna total se aplica el teorema de Thevenin para
calcular la Z y el teorema de Norton para calcular la Y.
3
2.
Teorema de Thevenin
El teorema establece que cualquier red lineal activa de dos terminales de las cuales
esta conectada una impedancia de carga que simbolizamos ZL se puede remplazar por
un circuito equivalente que consiste en una fuente de voltaje y una impeancia en serie,
como se muestra, de tal manera que por la ZL circulara la misma corriente o voltaje si
fuese en circuito original o el circuito equivalente de Thevenin1 :
Figura 1: Teorema de Thevenin
Para ello será necesario calcular o encontrar la impedancia de Thevenin y de igual
manera el Voltaje de Thevenin, que es precisamente la caı́da de voltaje que presenta en
circuito cuando es retirada la impedancia de carga del circuito original.
2.1.
Voltaje de Thevenin
Se retira la impedancia de carga ZL y se calcula el voltaje que se presente en las
terminales a y b donde se encontraba conectada dicha impedancia de carga. A este
voltaje lo conoceremos como el voltaje Vab o bien el voltaje de Thevenin Vth .
Figura 2: Voltaje de Thevenin
VT h = 3000j1 + 1800j2
Sistema de Ecuaciones Calculando las resistencias propias y mutuas
1
Circuitos electricos II, Benitez Serrano Ismael
4
R11 J1 + R12 J2 = 25
R21 J1 + R22 J2 = 0
R11 = 4800[Ω]
R22 = 8600[Ω]
R12 = R21 = −1800[Ω]
Sustituyendo en el sistema de ecuaciones:
4800J1 + (−1800)J2 = 25
−1800J1 +
8600J2 = 0
calculando
J1 =
Cof R11
∆
"
J1 = "
J2 =
25 −1800
0
8600
#
4800 −1800
−1800
8600
#
=
25(8600)
38040000
=
215000
38040000
Cof R22
∆
"
J2 =
4800 25
−1800 0
38040000
#
=
25(1800)
38040000
VT h = 3000J1 + 1800J2
VT h = 3000(5,65x10−3 ) + 1800(1,18x10−3 )
VT h = 19,07 [V olts]
2.2.
Impedancia de Thevenin
Para calcular la impedancia de Thévenin, deberemos pacificar el circuito (fuente de
corriente por un circuito abierto y fuente de voltaje por un corto circuito). Esto es con
el fin de dejar una estructura con solo elementos pasivos:
Como podemos observar la resistencia de 1,8[KΩ] se encuentra en paralelo con 3[KΩ],
que a su vez este paralelo se encuentra en serie con la de 1,8[KΩ] y finalmente en paralelo con 5[KΩ].
RP 1 =
1800∗3000
1800+3000
RP 1 = 1,125[KΩ]
5
Figura 3: Impedancia de Thevenin
RS1 = RP 1 + 1800
=
1125 + 1800
RS1 = 2,925[KΩ]
RP 2 =
RS1 ∗5000
RS1 +5000
=
2925∗5000
2925+5000
Req = RP 2 = ZT h
ZT h = 1,845[KΩ]
2.3.
Circuito equivalente Thevenin
Al circuito equivalente de Thevenin, le conectamos la ZL . Para el calculo final.
Figura 4: Circuito equivalente de Thevenin
J3 =
VT h
Rab +RL
J3 =
19,07[V ]
[(1845,74)+(480)]
=
8,202x10−3
J3 = IL
6
IL = 8,202x10−3 [A] ó 8,202[mA]
Calculando VRL para la misma resistencia.
V480 = IL ∗ ZL
V480 = (8,202x10−3 )(480)
VL = V480
VL = 3,94 [V olts]
7
3.
Teorema de Norton
El teorema establece que cualquier red lineal activa de dos terminales de las cuales
esta conectada una impedancia de carga que simbolizamos ZL se puede remplazar por
un circuito equivalente que consiste en una fuente de corriente y una impedancia en
paralelo, como se muestra la figura, de tal manera que por la ZL circulara la misma
corriente o voltaje si fuese en circuito original o el circuito equivalente de Norton2 :
Figura 5: Teorema de Norton
Para ello será necesario calcular o encontrar la impedancia de Norton y de igual
manera la corriente de Norton, que es precisamente la corriente que circula atravez del
corto circuito que presenta en circuito cuando es retirada la impedancia de carga y es
sustituida por un conductor en el circuito original.
3.1.
Corriente de Norton
Se retira la carga ZL y se calcula la corriente en las terminales a y b y ese será la Iab .
Calculando las resistencias propias y mutuas del circuito, tenemos.
Figura 6: Corriente de Norton
2
Ibide
8
R11 = 4,8[KΩ]
R22 = 8,6[KΩ]
R33 = 4,8[KΩ]
R12 = R21 = 1,8[KΩ]
R13 = R31 = −3[KΩ]
R32 = R23 = −1,8[KΩ]
R11 J1 + R12 J2 + R13 J3
R21 J1 + R22 J2 + R23 J3
R31 J1 + R32 J2 + R33 J3


4800
1800 25

8600 0 
 −1800

−3000 −1800 0
J3 = 
4800 −1800 −3000

8600 −1800
 −1800
−3000 −1800
4800
J3 =
25∗29,04x106
7,02x1010
=
= 25
= 0
= 0

=


726x106
7,02x1010
IN = J3
IN = 10,3x10−3 [A] ó 10,3[mA]
3.2.
Impedancia de Norton
Para calcular la impedancia de Norton al igual que la de Thevenin deberemos pacificar el circuito (fuente de corriente por un circuito abierto y fuente de voltaje por un
corto circuito). Esto es con el fin de dejar una estructura con solo elementos pasivos y
separando la ZL de la estructura original:
Figura 7: Impedancia de Norton
Como podemos observar la resistencia de 1,8[KΩ] se encuentra en paralelo con 3[KΩ],
que a su vez este paralelo se encuentra en serie con la de 1,8[KΩ] y finalmente en paralelo con 5[KΩ].
9
RP 1 =
1800∗3000
1800+3000
RP 1 = 1,125[KΩ]
RS1 = RP 1 + 1800
=
1125 + 1800
RS1 = 2,925[KΩ]
RP 2 =
RS1 ∗5000
RS1 +5000
=
2925∗5000
2925+5000
Req = RP 2 = ZT h
ZN = 1,845[KΩ]
Se realiza de igual manera que la Impedancia de Thevenin. En otras palabras Las
impedancias de norton y Thevenin son iguales. ZN = ZT h
3.3.
Circuito equivalente Norton
Al circuito equivalente de Norton reconectamos la Resistencia de carga.
Figura 8: Circuito equivalente de Norton
GN =
IN
VT h
=
10,6x10−3
15,57
Por divisor de corriente, tenemos:
−3 )(1845,43)
IL(500) = (10,3x10
1845,43+500
IL(500) = 8,1x10−3
ó 8,1[mA]
VL(500) = (8,1x10−3 )(500)
V(500) = 4,05[V olts]
10
4.
Conclusiones
Todo circuito lineal activo, puede ser reducido por un circuito equivalente serie
(Thevenin) o paralelo (Norton) www.esimez.virtual.ipn.mx
Para Thevenin
1. Retirar la impedancia de carga ZL .
2. Medir el voltaje (Vab ) en las terminales donde se encontraba la ZL
3. V[ ab] = VT h
4. Pacificar la red retirando las fuentes.
Las fuentes de voltaje se sustituyen con un corto circuito.
Las fuentes de corriente se sustityen con un circuito abierto.
5. Medir la impedancia equivalente (ZT h ) en las terminales donde se encontraba la
ZL
6. El circuito equivalente Thevenin será, colocando VT h en serie con la ZT h .
Para Norton
1. Retirar la impedancia de carga ZL .
2. Colocar un corto circuito en donde se encontraba la ZL .
3. Calcular la corriente (Iab ) que circula por el corto.
4. I[ ab] = IN
5. Pacificar la red retirando las fuentes.
Las fuentes de voltaje se sustituyen con un corto circuito.
Las fuentes de corriente se sustityen con un circuito abierto.
6. Medir la impedancia equivalente (ZT h ) en las terminales donde se encontraba la
ZL
7. El circuito equivalente de Norton será, colocando IN en paralelo con la ZN .
11
Índice de figuras
1.
2.
3.
4.
5.
6.
7.
8.
Teorema de Thevenin . . . . . . .
Voltaje de Thevenin . . . . . . .
Impedancia de Thevenin . . . . .
Circuito equivalente de Thevenin
Teorema de Norton . . . . . . . .
Corriente de Norton . . . . . . .
Impedancia de Norton . . . . . .
Circuito equivalente de Norton . .
.
.
.
.
.
.
.
.
12
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4
4
6
6
8
8
9
10