PR´ACTICA: ESTUDIO DEL CICLO BRAYTON
Anuncio

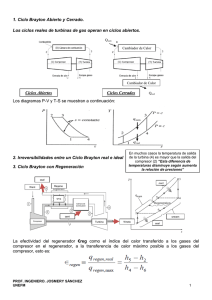
PRÁCTICA: ESTUDIO DEL CICLO BRAYTON 1. INTRODUCCIÓN En el análisis de los ciclos de turbinas de gas resulta muy útil utilizar inicialmente un ciclo ideal de aire estándar. El ciclo ideal de las turbinas de gas se llama ciclo Brayton, en honor del ingeniero estadounidense George Brayton. Comparado con los ciclos Otto y Diesel, el ciclo Brayton funciona en un intervalo más amplio de volúmenes, pero más reducido en presiones y temperaturas. Estas caracterı́sticas hacen que el ciclo Brayton no sea apto para ser utilizado en máquinas alternativas. En esta práctica vamos a analizar la influencia de distintos parámetros en el rendimiento de un ciclo Brayton simple. Para ello vamos a utilizar el programa informático CYCLEPAD. Figura 1: Diagramas p − v y T − s del ciclo Brayton 2. EL CICLO BRAYTON SIMPLE El ciclo ideal Brayton se compone de cuatro procesos internamente reversibles (ver figura 1): compresión adiabática (1−2), suministro de calor a presión constante (2−3), expansión adiabática (3−4) y cesión de calor a presión constante (4−1). Un análisis termodinámico de la instalación implica calcular el trabajo de compresión wc , el calor absorbido qabs , el trabajo de la turbina wt y el calor de desecho qced : wc = h1 − h2 ; wt = h3 − h4 (1) qabs = h3 − h2 ; qced = h1 − h4 (2) En un primer estadio del análisis de un ciclo Brayton se suele utilizar la hipótesis de aire estándar frı́o (los calores especı́ficos se suponen constantes e iguales a su valor a temperatura ambiente). Según esto, la ecuación (2) resulta: qabs = cp (T3 − T2 ) ; qced = cp (T1 − T4 ) (3) y el rendimiento térmico del ciclo es: η =1− |qced | (T4 − T1 ) T2 =1− =1− |qabs | (T3 − T2 ) T1 (4) Vemos que el rendimiento de un ciclo Brayton de aire estándar frı́o sólo depende de las temperaturas al inicio y al final del proceso de compresión, y es independiente de la máxima temperatura del ciclo T3 1 Un parámetro importante en un ciclo Brayton es la relación de presiones en el compresor y la turbina (o relación de compresión) r: p2 p1 r= (5) Teniendo en cuenta que el proceso 1−2 es isoentrópico, podemos obtener el rendimiento del ciclo en función de r a partir de la ecuación (4): η =1− 1 r(γ−1)/γ (6) donde γ = cp /cv es la relación de calores especı́ficos del gas. Por tanto, el rendiemitno térmico de un ciclo Brayton de aire estándar frı́o es función únicamente de la relación de compresión. 3. INFLUENCIA DE LA VARIACIÓN DE LOS CALORES ESPECÍFICOS El uso de los valores constantes de los calores especı́ficos, que nos llevó a las ecuaciones (4) y (6), es muy útil como modelo inicial de un ciclo de turbina de gas. No obstante, para obtener valores razonables de los términos de calor y trabajo en el análisis de un ciclo es necesario tener en cuenta la variación de cp con la temperatura. Vamos a ver que influencia tiene esta variación en el rendimiento del ciclo. Para ello vamos a analizar con el programa CYCLEPAD el rendimiento del ciclo Brayton para varios valores de r y dos valores distintos del calor suministrado qabs . 1. Descargamos el programa CYCLEPAD1 de http://www.uhu.es/gabriel.lopez/docencia.htm en el propio escritorio de nuestro ordenador. Ejecutamos el fichero cyclepad-2001-06-11.exe. 2. Abrimos el programa y construimos una turbina de gas uniendo un compresor, un quemador, una turbina y un enfriador. Seguidamente el programa nos pregunta si deseamos cambiar al modo de análisis. Al cambiar deberemos tener una imagen como la figura 2. Figura 2: Ciclo Brayton construido en CyclePad 3. Elegimos grados Kelvin (K) para la temperatura. 4. Pinchamos sobre el estado 1. Elegimos el aire como sustancia de trabajo. 5. Comenzamos primero con la opción de calores especı́ficos constantes, que por defecto es la que utiliza CYCLEPAD. 1 La página oficial del programa es http://www.qrg.northwestern.edu/projects/NSF/cyclepad/cyclepad.htm 2 6. Suponemos compresor y turbina isoentrópicas (Modeled as: works isentropically), y quemador y enfriador isobaros (Modeled as: works isobarically). 7. Tomamos en la ventana del estado 1: p1 = 1 bar, T1 = 395 K, ṁ1 =1 kg/s 2 . En la ventana del estado 2 elegimos p2 = 1,5 bar. En la ventana del quemador elegimos: GRUPO 1 qabs =600 kJ/(kg K); GRUPO 2 qabs =650 kJ/(kg K); GRUPO 3 qabs =650 kJ/(kg K); ... 8. Para obtener el rendimiento térmico del ciclo seleccionamos en la pestaña Cycle la opción Cycle Properties y seleccionamos la opción de que el ciclo es un motor térmico (Modeled as: CYCLE is a heat engine). Elaboramos una tabla donde escribiremos en una columna los valores de p2 , en otra el valor del rendimiento térmico del ciclo, en otra el trabajo neto y en otra la temperatura T3 . 9. Sin cerrar la ventana CYCLE, abrimos la ventana correspondiente del estado 2 y variamos los valores de la presión: (2.5, 3.5, 5.0, 7.5, 10.0, 12.5, 15.0, 17.5, 20.0) bar. Copiamos los correspondientes valores del rendimiento térmico, wnet y T3 en la tabla. 10. Repetimos el estudio anterior para los mismos valores de los parámetros pero eligiendo ahora la opción de calores especı́ficos variables: en la pestaña Edit elegimos Preferences, después Advanced y marcamos la casilla correspondiente a Use air standard. 11. Repetimos los pasos de 8 a 10, con los mismos valores de p y T pero para GRUPO 1 qabs = 1000 kJ/(kg K), GRUPO 2 qabs = 1100 kJ/(kg K), GRUPO 3 qabs = 1200 kJ/(kg K), ... 12. Represente gráficamente (en una sola gráfica) el rendimiento del ciclo en función de la relación de compresión para los cuatro casos considerados (a) cp = cte y qabs =600 kJ/(kg K), (b) cp variable y qabs =600 kJ/(kg K), (c) cp = cte y qabs =1000 kJ/(kg K)) (d) cp variable y qabs =1000 kJ/(kg K)). Discuta los resultados obtenidos. 13. Discuta cómo se modifican el trabajo neto y la temperatura máxima del ciclo cuando se tiene en cuenta la variación de cp con la temperatura. 4. RELACIONES DE TRABAJO MÁXIMO Hemos visto en la sección anterior que el rendimiento térmico aumenta al aumentar la relación de presiones; pero según aumenta r también aumenta T3 para una misma cantidad de calor absorbido. Esto tiene un inconveniente ya que esta temperatura podrı́a exceder el lı́mite metalúrgico permitido a la entrada de la turbina (unos 1200−1500 K). Para soslayar esta dificultad, se podrı́a proponer que r aumentara pero que la temperatura a la salida de la cámara de combustión (o a la entrada de la turbina) se mantuviera fija. Vamos a ver cómo con estas limitaciones, al aumentar r aumenta el rendimiento pero disminuye el trabajo neto obtenido wnet = wc + wt . Es decir, para alcanzar la misma potencia se necesitarı́a un flujo másico mayor, que a su vez requerirı́a un equipo mayor, lo cual tampoco es deseable. En el lı́mite cuando r se hace muy grande y la temperatura de salida de la cámara de combustión T3 se mantiene constante, el trabajo neto tiende a cero. También cuando r disminuye acercandose al valor 1 manteniendo T3 constante, el trabajo neto disminuye. Por tanto, dado un valor de T3 habrá un valor de r que lleve a un valor máximo de wnet . Si se considera un ciclo Brayton de aire estándar frı́o, el valor de r que hace wnet máximo viene dado por: ( r= 2 T3 T1 ) γ 2(γ−1) En verde aparecerán los valores asignados por nosotros y en azul los calculados por el programa. 3 (7) Vamos a estudiar el valor de r que implica el valor máximo de wnet para un valor fijo de T3 /T1 , teniendo en cuenta la variación de cp . 1. Sin abandonar el ciclo del apartado anterior, y suponiendo calores especı́ficos variables (tener marcada la casilla Use air standard ), tomamos p1 = 1 bar y T1 = 395 K. 2. Borramos el valor de qabs en la ventana del quemador (para ello pinchamos sobre el número en verde y seleccionamos Retract the value of ). Abrimos la ventana del estado 3 y asumimos un valor de: GRUPO 1 T3 = 1200 K, GRUPO 2 T3 = 1300 K, GRUPO 3 T3 = 1400 K, ... 3. Repetimos el procedimiento del punto 6 del apartado anterior: abrimos la ventana del estado 2 y variamos la presión p2 = (1.5, 2, 3, 4, 5, 6, 7, 8, 9, 10) bar. En una tabla copiamos los correspondientes valores del rendimiento térmico y del trabajo (potencia) neto. 4. Representar gráficamente el rendimiento térmico y el trabajo neto en función de r. 5. Demostrar que en el caso de un ciclo Brayton de aire estándar frı́o el valor de r para el cual wnet es máximo viene dado por la ecuación (7). (Ayuda: exprese el wnet en función de T1 , T3 y r. Derive wnet con respecto a r para obtener el máximo de la función). 6. ¿Para que valor de r se obtine el valor máximo de wnet ? Comparar este valor con el predicho por la ecuación (7) considerando calores especı́ficos constantes. Discuta los resultados obtenidos. 5. EFECTO DE LAS IRREVERSIBILIDADES DEL COMPRESOR Y LA TURBINA Para compresores y turbinas que funcionan casi adiabáticamente, el trabajo isoentrópico asociado a estos dispositivos es el modelo con el que comparar los equipos reales. Sin embargo, en la práctica, ambos dispositivos no son isoentrópicos y su funcionamiento se describe mediante un rendimiento adiabático. En la figura 2 se muestra en un diagrama T − s el efecto de las irreversibilidades en el ciclo Brayton. Figura 3: Efecto de las irreversibilidades del compresor y la turbina en un ciclo Brayton 4 Para el compresor, el rendimiento ηc se define como: ηc = ws h2s − h1 = wreal h2 − h1 (8) Y el rendimiento adiabático de la turbina ηt se define según: ηt = wreal h3 − h4 = ws h3 − h4s (9) Vamos a analizar el efecto cuantitativo de estas irreversibilidades con ayuda del programa CYCLEPAD, para varios valores de T3 /T1 . 1. Sobre el mismo ciclo que en los apartados anteriores, vamos a abrir las ventanas del compresor y de la turbina. Quitaremos la opción de dispositivo isoentrópico (Retract TUR works isentropically?) y elegiremos Modeled as: TUR works adiabatically. Seguidamente, en los parámetros casi al final asignaremos las correspondientes eficiencias adiabáticas especificados en el siguiente punto, en nu-s=UNKNOWN % 2. Tomamos p1 = 1 bar, T1 = 395 K y T3 = 2000 K. Los valores de los rendimientos adiabáticos son diferentes para cada grupo: GRUPO 1 ηc = 70 %, ηt = 95 %, GRUPO 2 ηc = 75 %, ηt = 90 %, GRUPO 3 ηc = 80 %, ηt = 85 %, GRUPO 4 ηc = 85 %, ηt = 80 %, GRUPO 5 ηc = 90 %, ηt = 75 %, GRUPO 6 ηc = 95 %, ηt = 70 %, GRUPO 7 ηc = 70 %, ηt = 70 %, GRUPO 8 ηc = 70 %, ηt = 80 %, GRUPO 9 ηc = 70 %, ηt = 90 % 3. La presión del estado 2 la variaremos según p2 = (2, 3, 4, 5, 6, 7, 8, 9, 10, 11) bar. En una tabla anotaremos los correspondientes valores del rendimiento térmico y trabajo neto. 4. Repetimos los apartados anteriores manteniendo los valores de todos los parámetros excepto T3 . Tomar T3 = 2100 K, 2200 K y 2300 K (son cuatro series en total contando con la del apartado del punto anterior). 5. Representar gráficamente (en una sola gráfica) el rendimiento térmico en función de r para los distintos valores de T3 /T1 considerados. Incluir en esta gráfica los valores del caso ideal correspondientes a GRUPO 1 T3 = 1200 K, GRUPO 2 T3 = 1300 K, GRUPO 3 T3 = 1400 K, ... (apartado anterior) para una mejor discusión de los resultados. 6. Representar gráficamente (en una sola gráfica) el trabajo neto en función de r para los distintos valores de T3 /T1 considerados. Incluir en esta gráfica los valores del caso ideal correspondientes a T3 = 1200 K (apartado anterior) para una mejor discusión de los resultados. 7. Discuta los resultados obtenidos. 5