tabla de derivadas derivadas de operaciones con funciones

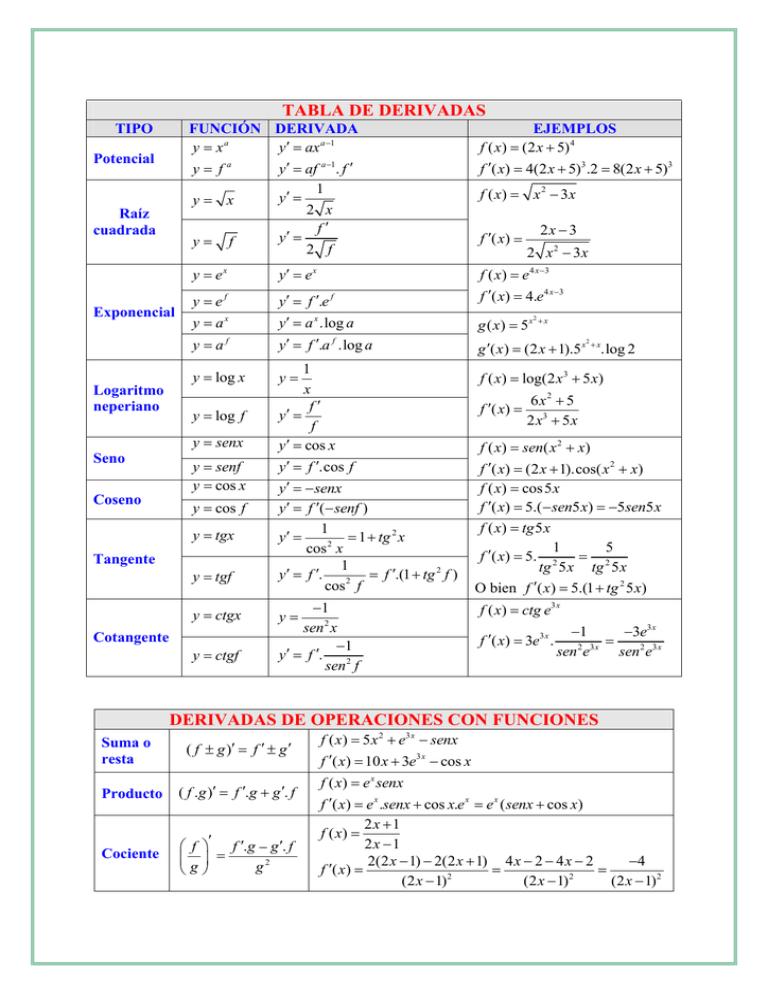
TABLA DE DERIVADAS
TIPO
FUNCIÓN DERIVADA
y = xa
y′ = ax a −1
y= fa
y′ = af a −1. f ′
1
y′ =
y= x
2 x
f′
y′ =
y= f
2 f
Potencial
Raíz
cuadrada
Exponencial
Logaritmo
neperiano
Seno
Coseno
EJEMPLOS
f ( x) = (2 x + 5) 4
f ′( x) = 4(2 x + 5)3 .2 = 8(2 x + 5)3
f ( x) = x 2 − 3x
f ′( x) =
2x − 3
2 x 2 − 3x
y = ex
y′ = e x
y = ef
y = ax
y′ = f ′.e f
y′ = a x .log a
g ( x) = 5x
y = af
y′ = f ′.a f .log a
g ′( x) = (2 x + 1).5 x + x.log 2
y = log x
1
x
f′
y′ =
f
y′ = cos x
y′ = f ′.cos f
y′ = − senx
y′ = f ′(− senf )
1
y′ =
= 1 + tg 2 x
2
cos x
1
y′ = f ′.
= f ′.(1 + tg 2 f )
2
cos f
y = log f
y = senx
y = senf
y = cos x
y = cos f
y = tgx
Tangente
y = tgf
y = ctgx
Cotangente
y = ctgf
y=
−1
sen 2 x
−1
y′ = f ′.
sen 2 f
y=
f ( x ) = e 4 x −3
f ′( x) = 4.e 4 x −3
2
+x
2
f ( x) = log(2 x 3 + 5 x)
f ′( x) =
6 x2 + 5
2 x3 + 5 x
f ( x) = sen( x 2 + x)
f ′( x) = (2 x + 1).cos( x 2 + x)
f ( x) = cos 5 x
f ′( x) = 5.(− sen5 x) = −5sen5 x
f ( x) = tg 5 x
1
5
f ′( x) = 5. 2 = 2
tg 5 x tg 5 x
O bien f ′( x) = 5.(1 + tg 2 5 x)
f ( x) = ctg e3 x
f ′( x) = 3e3 x .
−1
−3e3 x
=
sen 2 e3 x sen 2 e3 x
DERIVADAS DE OPERACIONES CON FUNCIONES
Suma o
resta
( f ± g )′ = f ′ ± g ′
Producto
( f .g )′ = f ′.g + g ′. f
Cociente
 f ′ f ′.g − g ′. f
  =
g2
g
f ( x) = 5 x 2 + e3 x − senx
f ′( x) = 10 x + 3e3 x − cos x
f ( x) = e x senx
f ′( x) = e x .senx + cos x.e x = e x ( senx + cos x)
2x +1
f ( x) =
2x −1
2(2 x − 1) − 2(2 x + 1) 4 x − 2 − 4 x − 2
−4
=
=
f ′( x) =
2
2
(2 x − 1)
(2 x − 1)
(2 x − 1) 2