T - U-Cursos
Anuncio
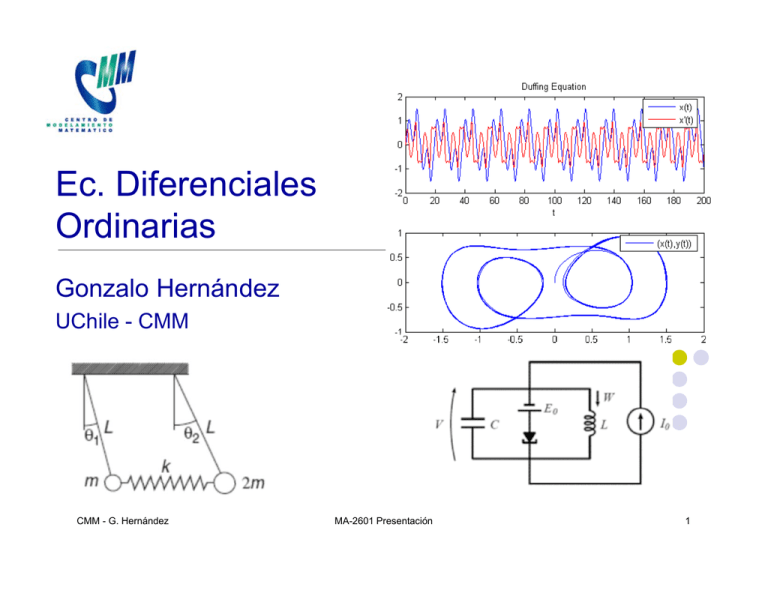
Ec. Diferenciales Ec Ordinarias Gonzalo Hernández UChile - CMM CMM - G. Hernández MA-2601 Presentación 1 Descripción EDO: Objetivos 1) Resolver edo y sistemas lineales edo usando métodos clásicos. 2) Interpretar I t t geométricamente ét i t ell problema bl de d valor l inicial i i i l en términos de curvas integrales. 3) Aplicar el teorema de existencia y unicidad y conocer ejemplos donde no hay unicidad o existencia global. 4) Conocer y aplicar los métodos numéricos de Runge Runge-Kutta Kutta de orden 2 y su implementación en Matlab, Maple o Scilab. 5) Estudiar el comportamiento cualitativo de sistemas no lineales. 6) Comprender el rol de las edo en la modelación de fenómenos de la vida real; péndulo no-lineal, sistemas lineales de vibraciones mecánicas, modelos de dinámica de poblaciones. CMM - G. Hernández MA-2601 Presentación 2 Programa EDO 0) Motivación: Modelación utilizando EDO 1) EDO de primer orden (3 semanas) 2) EDO lineales de orden n (4 semanas) 3) Transformada de Laplace (2 semanas) 4) Sistemas lineales de EDO (3 semanas) 5) Sistemas no lineales de EDO (3 semanas) CMM - G. Hernández MA-2601 Presentación 3 Programa EDO 0) Motivación: Modelación utilizando EDO 1)) EDO O de primer orden (3 ( semanas)) Descripción cualitativa edo primer orden. Curva integral Ecuaciones de variable separable separable. Ecuaciones homogéneas homogéneas. Modelación usando EDOs de primer orden. Resolución EDO lineales de primer orden homogéneas y no homogéneas utilizando el factor integrante. Ecuación de Bernoulli y de Ricatti. Teorema de existencia y unicidad para problema valor inicial. Métodos numéricos tipo Runge-Kutta. CMM - G. Hernández MA-2601 Presentación 4 Programa EDO 2) EDO lineales de orden n (4 semanas) Existencia de base soluciones de edo lineales homogéneas de orden n. Wronskiano. Edo lineales homogéneas orden 2. Fórmula Abel. Problema vibraciones mecánicas. Edo lineales no homogéneas orden 2. Fórmula de variación de parámetros Función de Green parámetros. Green. Edo lineales de orden 2 con condiciones de borde. Series de potencia para edo no homogéneas de orden 2 con puntos singulares. Método de Frobenius. Edo lineales homogéneas orden n. Polinomio característico. Ecuación de Euler – Cauchy. Edo lineales no homogeneas orden n. Met. coef. indeterminados. CMM - G. Hernández MA-2601 Presentación 5 Programa EDO 3) Transformada de Laplace (2 semanas) Definición Definición, ejemplos y fórmulas básicas. básicas Fórmula de convolución. convolución Resolución de edo lineales usando transformada de Laplace. Función de Heaviside y delta de Dirac. Resolución de edo lineales con lados derechos generalizados. 4) Sistemas lineales de EDO (3 semanas) Problema valor inicial para un sistema lineal lineal. Matriz fundamental fundamental. Problema de valor inicial para un sistema lineal a coeficientes constantes. Cálculo de la matriz exponencial. Análisis del comportamiento asintótico de las soluciones en función de los valores propios. Diagramas g de fase p para el caso 2x2. Fórmula de variación de parámetros para sist. Lineales no homog. CMM - G. Hernández MA-2601 Presentación 6 Programa EDO 5) Sistemas no lineales de EDO (3 semanas) Sistemas Si t hamiltonianos h ilt i y conservación ió d de energía. í A Análisis áli i d de algunos casos simples. C Clasificación as cac ó de puntos pu os críticos. c cos Estabilidad s ab dad asintótica. as ó ca Uso de coordenadas polares. Análisis de algunos sistemas no-lineales clásicos: Sistema de Volterra. Funcional de Lyapunov y estabilidad. Estudio de sistemas que provienen de gradientes gradientes. CMM - G. Hernández MA-2601 Presentación 7 Organización de la Sesiones 2 Clases de cátedra a la semana: Martes y jueves 14:30 hrs. 1 Clase auxiliar a la semana: Viernes 14:30 hrs. Francisco Bravo Pedro Montealegre En U-Cursos se publicará el material del curso: Clases + Notas + Laboratorios + Pautas CMM - G. Hernández MA-2601 Presentación 8 Evaluación 1) Tres controles (semanas 4,8,12). Nota eximición según reglamento: 5.5 2) Ayudantía + Laboratorios Matlab: L1: Algebra Lineal Numérica L2: Ecuaciones Diferenciales L3: Sistemas de Ecuaciones Diferenciales 3) Cálculo nota final: NF = (NC)*0.75 + (NA)*0.25 CMM - G. Hernández MA-2601 Presentación 9 Evaluación: Laboratorio de Matlab para EDO 1) Capacidades básicas de cálculos matemáticos 2) Herramientas H i t d de visualización i li ió d de resultados lt d 3) Más de 30 Toolboxes: Curve Fitting Fitting, Splines Splines, Optimization Optimization, PDE, PDE Symbolic, Symbolic Statistics Neural Networks, Genetic Algorithms, etc. Signal & Image Processing, Bioinformatics, Control, Financial, etc. 4) Funciones .m y programación 5) Tools: Taylor, Spline, Curve Fiiting, etc 6) Help ! , Libros, Manuales 7) File Exchange, Webminars 8) Cálculos complejos lentos + Traducción a C/C++ deficiente Gonzalo Hernández Laboratorio MA-43B 10 Evaluación: Laboratorio de Matlab para EDO Objetivos del Laboratorio: Utilizar Utili algunos l Mét Métodos d Numérico N éi +M Matlab tl b como herramienta para resolver edos no lineales. Ingeniería Conocer algunos modelos en en Ciencias e Ingeniería. Algunos links de interés: Home Matlab: http://www.mathworks.com/ p Documentación Oficial: http://www.mathworks.com/access/helpdesk/help/helpdesk.ht ml File Exchange: http://www.mathworks.com/matlabcentral/fileexchange/ Gonzalo Hernández Laboratorio MA-43B 11 Motivación EDO Desde el siglo 18, las leyes físicas del universo han sido descritas principalmente, descritas, principalmente por edo o edp. edp Estas ecuaciones tienen derivadas de funciones que se desconocen y que representan la fuerza, presión, temperatura, potencial electromagnético, etc. La edo más conocida es la segunda ley de Newton: 2x d f m 2 ft dt donde x(t) es la posición de un cuerpo de masa m, constante que se mueve horizontalmente debido a la acción constante, de una fuerza f(t). Esta ley que fue publicada en 1687 en la obra "Philosophiae Naturalis Principia Mathematica". CMM - G. Hernández MA-2601 Presentación 12 Motivación EDO CMM - G. Hernández MA-2601 Presentación 13 Motivación EDO En Ciencia e Ingeniería, las ec. diferenciales representan (modelan) el comportamiento de un sistema real real. Se obtienen como resultado de un proceso iterativo de abstracción análisis, abstracción, análisis hipótesis, hipótesis verificación y validación. validación Se pueden clasificar de acuerdo a: Tipo: p Ordinaria o p parcial Orden: Primer o orden superior Linealidad o No-Linealidad Coeficientes: Constantes o Variables Lado derecho: Homogénea o No Homogénea Forma general de una edo lineal: dn y d2 y dy a x a x a x a 0 xy Qx n 2 MA-2601 Presentación 1 n CMM - G. Hernández 2 dx dx dx 14 Motivación: Modelación con EDO Trayectorias de partículas: Caída Libre y m x g mx mg f R ( x ) mg cx 2 Lanzamiento de proyectiles Movimiento planetario CMM - G. Hernández MA-2601 Presentación Coeficiente de viscosidad 15 Motivación: Modelación con EDO Trayectorias de partículas: Ecuación del Péndulo Simple: 2 d m s −mg sin dt d 2 − g sin i dt l sin − 16 3 1 120 5 O 7 d2 ≈ − g l dt t ≈ c 1 sin CMM - G. Hernández MA-2601 Presentación g l t c 2 cos g l t 16 Motivación: Modelación con EDO Movimiento armónico: Masa colgando de un resorte k x<0 L x>0 2 d m 2x mg − kx dt mg − kx − L x CMM - G. Hernández MA-2601 Presentación 17 Motivación: Modelación con EDO Movimiento armónico: Ejemplo simple 2 d m 2x F E F R Ft dt −kx − mg Ft CMM - G. Hernández MA-2601 Presentación 18 Motivación: Modelación con EDO Movimiento armónico acoplado: Ejemplo simple CMM - G. Hernández MA-2601 Presentación 19 Motivación: Modelación con EDO Movimiento armónico acoplado: Masas colgando de resortes t CMM - G. Hernández MA-2601 Presentación 20 Motivación: Modelación con EDO Movimiento armónico: Masas ligadas por un resorte kL 2 − 1 − mg sin 1 mL 1 − kL 2 − 1 − 2mg sin 2 2mL 2 Esta edo de segundo orden se puede llevar a un sistema de edo de primer orden, utilizando las transformaciones: y 1 t 1 t CMM - G. Hernández y 2 t 2 t y 3 t MA-2601 Presentación d 1 dt y 4 t d 2 dt 21 Motivación: Modelación con EDO Movimiento Armónico: Masa ligada a resorte en ángulo x µ=0 L0 m k Lx00 d2x k x 1 2 2 dt m x2 L0 CMM - G. Hernández MA-2601 Presentación 22 Motivación: Modelación con EDO Ecuación de Duffing: E t edo Esta d no-lineal li l se utiliza tili para d describir ibi dif diferentes t sistemas dinámicos (resortes, transformadores, etc). La forma más general de esta ec ecuación ación es es: d 2 x(t ) dx(t ) 3 2 x ( t ) 0 x (t ) cos t 2 dt dt Por ejemplo, la edo del flujo magnético de un transformador tiene la forma: 3 2 b 0 E cos t N CMM - G. Hernández MA-2601 Presentación 23 Motivación: Modelación con EDO Ejemplo Ecuación de Duffing: x x x3 0 2 x cos t 1, 1, 0 1 1, 1, 0 Ejemplo de caos “ordenado” CMM - G. Hernández MA-2601 Presentación 24 Motivación: Modelación con EDO Modelo de Crecimiento Logístico de una Población: L población La bl ió p(t) (t) de d EEUU en ell siglo i l 20 crece aproximadamente según la edo no lineal logística: dp pt − pt 2 ∀t ∈ t 0 , T dt p0 p 0 Aplicando un proceso de ajuste de parámetros, los modeladores determinaron que: α=0.02 β=0 00004 β=0.00004 CMM - G. Hernández MA-2601 Presentación 25 Motivación: Modelación con EDO Modelo de Crecimiento Logístico de una Población: Año Tiempo t k pt real [millones de personas] Año Tiempo t k pt real [millones de personas] 1890 -10.0 62.9798 1900 0.0 76.2122 1880 -20.0 20.0 50.1892 1910 10.0 92.2285 1870 -30.0 38.5584 1920 20.0 106.0215 1860 -40.0 31.4433 1930 30.0 123.2026 1940 40 0 40.0 132 1646 132.1646 1950 50.0 151.3258 1960 60.0 179.3232 1970 70.0 203.3020 1850 -50.0 23.1919 1840 -60.0 17.0634 1830 -70 70.00 12 8607 12.8607 1820 -80.0 9.6384 1980 80.0 226.5422 1810 -90.0 7.2399 1990 90.0 248.7099 1800 -100.0 5.3085 2000 2010 100.0 281.4219 CMM - G. Hernández MA-2601 Presentación 26 Motivación: Modelación con EDO De acuerdo a los datos reales de la transparencia anterior: Se S puede d afirmar fi que ell modelo d l es adecuado d d ? Cuál es error entre 1900 y 1980 ? dp p (t ) p 2 (t ) dt solución 500 p (t ) 1 4239 50 t exacta 1+ 761 e pk 1 pk h( pk pk 2 ) pk p(t tk ) k 0,...,8 n CMM - G. Hernández (T t0 ) (1980 1900) 10 h n 8 tk hk 10 k k 0,1,...,8 MA-2601 Presentación 27 Motivación: Modelación con EDO Modelo de Crecimiento Logístico de una Población: Añ Año Ti Tiempo tk p(t) (t) reall p(t) (t) Edo Ed p(t) (t) Euler E l E 1 Error1 E 2 Error2 1900 0.0 76.1 76.1 76.1 0.0 0.0 1910 10.0 92.4 89.9 89.0 2.5 0.9 1920 20.0 106.5 105.6 107.5 0.9 -1.9 1930 30.0 123.1 123.2 123.3 -0.1 -0.1 1940 40.0 132.6 142.7 141.7 -10.1 1.6 1950 50.0 152.3 164.0 152.1 -11.7 11.9 960 1960 60.00 60 180.7 80 186.7 86 173.5 35 -6.0 60 13.2 3 1970 70.0 204.9 210.6 203.8 -5.7 6.8 1980 80.0 226.5 235.3 229.1 -8.8 6.2 1990 90.0 248.7 260.3 253.9 -11.6 6.4 2000 100.0 281.4 MA-2601 Presentación 285.1 278.9 -3.7 6.2 28 CMM - G. Hernández Motivación: Modelación con EDO El modelo de Lotka - Volterra predice la evolución de una población con especies depredadora x1(t) y presa x2(t). (t) Se supone que la población presa tiene suficiente comida y que su natalidad es proporcional a la cantidad de presas vivas: k1x1(t). La mortalidad de la población presa depende del número de presas y depredadores: k2x1(t)x2(t). La natalidad de la p población depredador p es: k3x1((t)x ) 2((t)) y su mortalidad es: k4x2(t). Se expresa el cambio en la poblaciones presa y depredador mediante el sistema de edos: CMM - G. Hernández MA-2601 Presentación 29 Motivación: Modelación con EDO dyy 1 dt k1 dyy 2 dt k3 CMM - G. Hernández k 1 y1 − k 2 y1 y2 3 k 2 0. 002 y 1 t 0 1 1000 k 3 y1 y2 − k 4 y2 0. 0006 k 4 0. 5 y 2 t 0 1 500 MA-2601 Presentación 30 Motivación: Modelación con EDO El proceso químico de decaimiento del ozono (O₃) en la alta lt atmósfera t ó f debido d bid all efecto f t de d la l radiación di ió d dell soll se describe mediante la fórmula: Donde dy 1 −k 1 y 1 y 3 k 2 y 2 y 23 − k 3 y 1 y 2 dt dy 2 k 1 y 1 y 3 − k 2 y 2 y 23 − k 3 y 1 y 2 dt dy 3 −k 1 y 1 y 3 k 2 y 2 y 23 k 3 y 1 y 2 dt k₁,k₂,k₃ son los parámetros cinéticos y₁,y₂,y₃ y₁ y₂ y₃ son las concentraciones de O₃ O₃,O,O₂ O O₂ CMM - G. Hernández MA-2601 Presentación 31 Motivación: Modelación con EDO Para simplificar este sistema usualmente se supone que la concentración t ió d de O O₂ es constante. t t Dándole Dá d l valor l a llas constantes y re-escalando se obtiene el sistema: dy 1 −y 1 − y 1 y 22 294y 2 y 1 0 1 dt y − y 1 y 2 dy 2 1 − 3y 2 y 2 0 0 98 dt CMM - G. Hernández MA-2601 Presentación 32 Bibliografía: 1) Burden, R., J. D. Faires, Análisis Numérico, Séptima Edi ió Thomson Edición, Th L Learning, i 2002 2002. 2) Gerald, C.F., P.O. Wheatley, Applied Numerical Analysis, Pearson 2004 Pearson, 2004. 3) Gilat, A., MATLAB: An Introduction with Applications, John Wiley & Sons Sons, 2008 2008. 4) Kiusalaas, J., Numerical Methods in Engineering with Matlab Cambridge University Press Matlab, Press, 2005 2005. 5) Yang, W.Y., W. Cao, T.S. Chung, J. Morris, Applied Numerical Methods Using MATLAB MATLAB, by by, Wiley Wiley, 2005 2005. CMM - G. Hernández MA-2601 Presentación 33