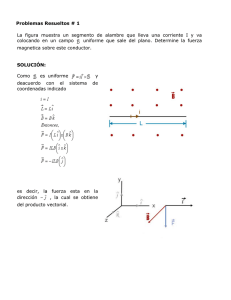
Demostrar que si tenemos un campo magnético uniforme en la
Anuncio

Demostrar que si tenemos un campo magnético uniforme en la dirección del eje Z, el potencial vectorial es ~ = 1 ~r B ~ A 2 Solución: Tenemos que ~ =r A ~ B así que 1 ~ ~=r ~r B r A 2 Usando que ~ = G ~ r F~ G ~ r F~ ~ + F~ r G ~ r F~ G F~ r G tenemos h i 1 ~ = 1 B ~ r ~r B ~ (r ~r) (~r r) B ~ + ~r r B ~ ~=r ~r B r A 2 2 Basta una simple inspección para cerciorarse que ~ r ~r = B ~ B Sabemos que siempre ~ =0 r B Como el campo es uniforme ~ =0 (~r r) B Es sencillo demostrar que además r ~r = 3 Así que ~ 3B ~ ~= 1 B r A 2 y …nalmente encontramos lo que queríamos demostrar ~=B ~ r A 1