UNIDAD DIDÁCTICA III: “Las formas tridimensionales”. (Pág. 29 39)

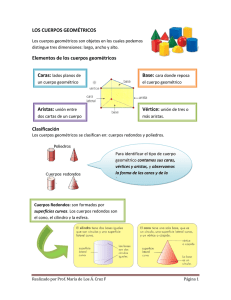
 UNIDAD DIDÁCTICA III: “Las formas tridimensionales”. (Pág. 29 ­39)
1ª ¿Cuáles son los elementos que definen las formas tridimensionales? (0,8 puntos)
Cara Son polígonos regulares o irregulares que limitan determinados volúmenes. Arista segmento de recta formada por la intersección de dos caras contiguas de una superficie poliédrica .
Vértice punto común a tres o más aristas de un cuerpo poliédrico, el más alejado de la base de un cono.
Superficie curva Se desvía constantemente un plano sin formar ángulos . 2ª ¿Qué son los Poliedros? (0,8 puntos)
Son cuerpos tridimensionales delimitados por caras poligonales. Cuando los poliedros tienen todas las caras en forma de polígono regular y todas son iguales, se denominan poliedros regulares. Otros poliedros que no tienen todas las caras iguales son las pirámides (caras triangulares excepto la base poligonal) , tronco de pirámide (si un plano corta las caras laterales) y los prismas (caras con forma de cuadriláteros excepto las bases de forma poligonal). Unos y otros pueden ser rectos u oblicuos. 3ª ¿Cuáles son los Poliedros regulares? (0,8 puntos)
Sólo hay cinco poliedros regulares: El tetraedro (4 caras en forma de triángulos equiláteros ), Hexaedro o cubo (6 caras cuadradas ), Octaedro (8 caras en forma de triángulos equiláteros ), Dodecaedro (12 caras en forma de pentágonos regulares ) e icosaedro (20 caras en forma de triángulos equiláteros )
4ª Los cuerpos de revolución (0,8 puntos)
Estos cuerpos están delimitados por superficies curvas. Pueden obtenerse haciendo girar una figura plana alrededor de un eje, estos pueden ser: El cono, Tronco de cono, Cilindro y Esfera.
El cono se genera haciendo girar un triángulo rectángulo alrededor de uno de sus catetos. El tronco de cono se obtiene cortando un cono con un plano. El cilindro se genera haciendo girar un rectángulo sobre uno de sus lados. La esfera se obtiene haciendo girar un semicírculo sobre su diámetro 5ª La estructura geométrica en el cuerpo humano (0,8 puntos)
Podemos comparar la estructura de la cabeza de una persona con la de un huevo dividido verticalmente en dos partes iguales. Los elementos de la cara, boca, nariz, ojos y cejas se reparten simétricamente a ambos lados de este eje central. Los ojos están situados, aproximadamente, a la mitad de la altura de la forma oval, y si dividimos esta altura en tres partes iguales, obtenemos la posición de las cejas y de la base de la nariz
6ª La simetría y tipos de simetría. (1,2 puntos)
Es la organización armónica de la forma, posición y tamaño de algunos objetos, tanto naturales como artificiales que tienen como referencia un punto, una recta o un plano. Podemos distinguir los siguientes tipos de simetría: –En formas bidimensionales: Simetría axial: los puntos equidistan de un eje central
Simetría central: cada elemento tiene otro simétrico y opuesto con respecto a un punto.
–En formas tridimensionales: Simetría bilateral en el espacio: un plano divide en dos mitades.
Simetría axial en el espacio: una serie de planos que pasan por un eje de giro.
Simetría central en el espacio: los extremos de los posibles diámetros son simétricos con respecto a un centro de simetría.
7ª El sistema diédrico. (0,8 puntos)
El sistema diédrico representa un cuerpo mediante dos dibujos que corresponden a puntos de vista extremos: el alzado, que lo representa visto de frente y la planta, que muestra el objeto visto desde arriba. Muchas veces resulta necesario añadir un dibujo auxiliar que muestra el objeto de lado, la vista lateral o de perfil, a fin de describirlo perfectamente. 8ª Las perspectivas. (1,2 puntos)
Las perspectivas se basan en Sistemas de Representación que pretenden representar el volumen de los objetos de una manera cintífica y técnica. Hay dos Sistemas diferentes:
1­ La perspectiva Axonométrica Para simplificar la representación de los objetos, hay perspectivas como la Axonométrica que evitan los puntos de fuga y basan la representación del volumen en tres ejes, que plasman las tres direcciones del espacio: la altura (Z), la anchura (X) y la profundidad (Y). Todas las líneas que representan una determinada dirección se dibujan paralelas al eje correspondiente. Según la colocación de estos tres ejes, se obtienen las diferentes perspectivas del sistema axonométrico: Perspectiva caballera, Perspectiva isométrica y Perspectiva militar.
2­ La perspectiva Cónica. Es la perspectiva que mejor imita la visión del ojo humano. Para conseguirlo, todas las líneas que en el espacio son paralelas se representan convergiendo o se juntan en un punto imaginario, denominado punto de fuga. 9ª Maurits Cornelis Escher y las Figuras imposiles (0,8 puntos)
M. C. Escher (1898­1972) Nació en los Países Bajos artista estudiado por los matemáticos por su gran dominio de las leyes de la Perspectiva para la representación del espacio, “ilusiones ópticas” y las “figuras imposibles” que son imposibles de realizar tridimensionalmente.
Representó imágenes como la “cinta de Moebius”, u objetos imposibles com el “cubo de NecKer” o el “triángulo de Penrose”.
En otras obras hizo uso de redes poligonales o siemetrías en las que las figuras se van transformando.