Formalización. Conectivas y constantes lógicas.

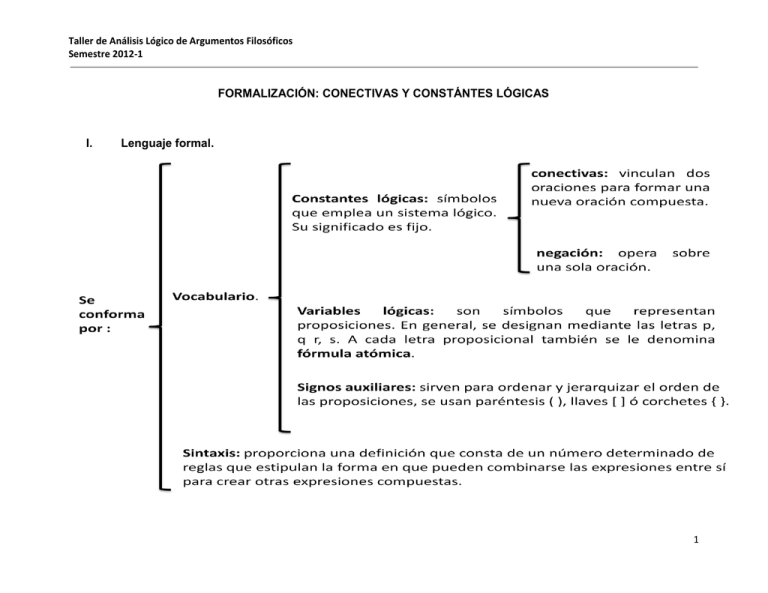
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
FORMALIZACIÓN: CONECTIVAS Y CONSTÁNTES LÓGICAS
I.
Lenguaje formal.
1
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
II.
Definición y utilidad de la formalización
Formalización es el proceso de traducción de los argumentos del lenguaje natural a esquemas de argumentos de un
lenguaje simbólico artificial.
¿Para qué nos sirve el lenguaje simbólico artificial (lenguaje formal) en lógica?
1.- Para poder evaluar la corrección o validez de un argumento librándonos de la ambigüedad, vaguedad, el equívoco y
distracción emotiva que presenta el lenguaje natural.
2.- Nos es útil para observar con mayor claridad la estructura lógica del argumento, cuyas formas pueden ser oscurecidas
por el lenguaje ordinario.
3.- Nos facilita la extracción de inferencias y por lo tanto nos ayuda a la comprensión del argumento en cuestión.
III.
Formalización de un argumento
Para la formalización será importante tener los siguientes elementos:
Nombre: nombrar nuestra formalización será importante para poder distinguirla de otras que contemplen una
interpretación diferente del mismo argumento.
Diccionario de proposiciones atómicas: elaborar este diccionario nos ayudará a poder identificar claramente cada una
de las premisas. Hay que tener en cuenta que una proposición atómica es aquel enunciado que tiene un sólo sujeto,
verbo y predicado. Es importante diferenciar las proposiciones atómicas de las proposiciones moleculares, que son
aquellas que pueden estar compuestas de dos o más atómicas unidas por alguna conectiva.
Asignación de valores de verdad: Para poder evaluar la corrección o validez del argumento necesitaremos otorgarle a
cada proposición un valor de verdad específico: verdadero (V) o falso (F).
2
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
Diccionario de definiciones conceptuales: Nos ayuda a evitar la ambigüedad o vaguedad1 en alguno de los términos
que se utilizan en el argumento.
IV.
Estrategias para traducir proposiciones del español al lenguaje de lógica proposicional.
1.- Tratar de identificar las ideas principales que se encuentran en el texto. Estas se pueden reconocer porque suelen
estar separadas por puntos o, en el caso de la conclusión, por un indicador de inferencia o nexo inferencial (“por lo tanto”,
“de aquí se sigue que”, “esto implica”).
2.- Diferenciar aquellas ideas principales que están formadas por una sola proposición atómica o enunciado simple. Un
modo sencillo de hacerlo es identificando los nexos que están uniendo varios enunciados dentro de una idea, a estos
nexos se les llama también conectivas.
3.- Después de haber obtenido los enunciados o proposiciones más simples, ha de analizarse qué tipo de conectivas las
están uniendo y entonces, asignar un símbolo tanto a unos como a otros.
V.
Estrategias para traducir proposiciones de lenguaje de lógica proposicional al español.
1.- Identificar si las premisas y la conclusión son moleculares o atómicas.
2.- Si las premisas son moleculares habrá que identificar el tipo de conectivas que las une, estas nos indicarán cuál es la
relación entre los enunciados que habrá que traducir a lenguaje natural.
3.- Se asignan ideas a cada símbolo proposicional del modo que sea más acorde a lo que implican las conectivas. Es
importante tratar de que el texto en español tenga un grado considerable de cohesión.
1
Un término es ambiguo cuando tiene más de un significado, en un contexto dado, y éste no nos aclara su uso específico. Es vago cuando existen “casos
límites” y no es posible determinar si el término se aplica o no a ellos.
3
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
VI.
Tipos de Conectivas.
Conectiva
Negación (¬)
Características
Ejemplo
Tabla de verdad
Afirma la falsedad de algo, indica que El dinero no es la felicidad.
P
-P
algo no está pasando, que algo en
mentira.
No es el caso que el dinero
V
F
es la felicidad.
F
Conjunción (^)
Disyunción (^)
Une dos proposiciones que se están Sonia hace la tarea mientras
dando de manera simultánea. Los escucha música.
enunciados que une son conocidos
como conyuntos.
Demóstenes canta, baila y se
despeina en el concierto.
Expresa una alternativa entre dos
hechos. Cada una de sus partes se
llama disyuntos. Existen dos tipos de
disyunciones:
Disyunción exclusiva: puede que se Estudias lógica o te duermes.
de uno u otro hecho, pero no ambos
al mismo tiempo.
V
P
Q
V
V
F
F
V
F
V
F
V
F
F
F
P
Q
P v Q
V
V
F
F
V
F
V
F
V
V
V
F
P
^ Q
Disyunción inclusiva: se puede dar Estudias lógica o te rascas.
4
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
Condicional
(→)
uno u otro hecho, o ambos a la vez.
material La relación aquí expresada es una de Si estudio para mi examen,
necesidad y suficiencia. Esto es, entonces aprobaré.
cuando se habla de que algo es
necesario para que pase otra cosa o
cuando se habla de que cuando pasa
algo se presupone que también
pasaron muchas otras cosas que lo
hicieron posible.
P
Q
P ⊃ Q
V
V
F
F
V
F
V
F
V
F
V
V
P
Q
P ≡ Q
V
V
F
F
V
F
V
F
V
F
F
V
La que es suficiente se conoce como
antecedente y va del lado izquierdo
de la conectiva; y la que es necesaria
es llamada consecuente y se coloca
del lado derecho.
Bicondicional material Se encuentra una relación entre
sucesos parecida a la del condicional,
(↔)
pero
en
este
caso
ambas
proposiciones son suficientes y
necesarias para la otra.
VII.
Es necesario y suficiente que
me hayan dado mi título para
saber que me titulé y a la
inversa.
Límites del lenguaje proposicional
5
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
Al formalizar un argumento utilizando lenguaje de lógica proposicional hay varias cosas o cierto tipo de información
que no es posible rescatar.
a) Temporalidad: las oraciones “Ayer comí carne” y “Mañana comeré carne” se han de formalizar con letras distintas y
entonces se pierde la idea de que ambas hablan de la misma acción realizada por el mismo sujeto pero en
distintos momentos, al formalizar dichas frases ya no se puede ver si hay o no relación entre ellas.
b) Causalidad: en el lenguaje proposicional no hay una conectiva capaza de denotar una relación de causalidad. La
relación que propone el condicional material es hipotética, si pasara esto, entonces, pasaría esto otro.
c) Cuantificacionalidad: no se puede distinguir entre sujetos generales o particulares. pues no es lo mismo decir que
“todos corre por la calle” a decir que “mi primo corre por la calle”.
d) Otras nociones que se pierden son aquellas del deber, querer, esperar, necesitar, etc. No es lo mismo necesitar ir
a la escuela que esperar ir a la escuela.
VIII.

Ejemplo de formalización.
Los juicios estéticos ni son objetivos, ni son universales. Por tanto, tampoco son a priori.
Interpretación: estética.
Diccionario de proposiciones atómicas:
p: los juicios estéticos son objetivos. F
q: los juicios estéticos son universales. F
r: los juicios estéticos son a priori. F
6
Taller de Análisis Lógico de Argumentos Filosóficos
Semestre 2012-1
Diccionario de definiciones:
Objetivo: que existe independientemente de la percepción individual.
A priori: que existe independientemente de la experiencia.
Traducción:
(¬p ^ ¬q) → ¬r
7