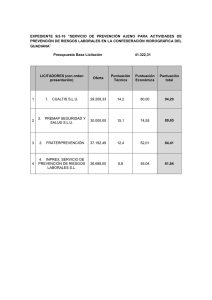
Diédrico - Figuras Planas

oS lca
x.* oPclóN t¡ 10: SI§TEMA
._
DIEDRIGO
_L_
EJERCIC¡O
pide:
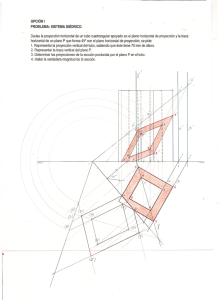
Dada lalrazahorizontal del plano P y las proyecciones de una recta R contenida en é1, se
plano
P1. Dibujar latraza verticaldel
proyección.
2. úeteirminar nJañgutos quá fonna la recta R con los planos horizontal.y vertical.de
proyecciÓn.
y
verticalde
horizontal
plano
los'planos
P
con
et
fonna
ánóutos
3. Determ¡nar iói
{ue
,/t/é
$\\
L-l
t.;
i-a
p
¡t
(vt
[t
Puntuación:
Apartado 1:
Apartado 2:
Apartado 3:
1 punto
I punto
1 punto
Puntuación máxima: 3 puntos
oPcÉN
il
oY
loí
EIERCIGIO 10: SISIETIIA DIÉDRGO.
Dadas las proyecciones del punto A, se pide:
punto A y forma 45o con el phno
del dano P que, siándo paralelo a la llnea de tiema, ontisre al
;tó;brrr ¡*
y lV'
horironial de proytccién. Noh: el plano P pasa po los orad¡antes l, ll
de tierra'
r .i tugar georetrico de los puntos del plano P que dhhn 3 crn de la lír¡ea
t *.
,tñrp"r".t
s
Puntuación:
Apartado
1
Apartado 2
1 punto
2 puntos
Puntuación máxima: 3 ountos
oPcrÓN il
EJERCICIO
I":
SISTEMA DIÉDRCO.
Dadas las trazas del plano P y la traza hoüontal del plano proyectante Q, asi como las proyecciones del punto A, se
pide:
Dibular las proyecciones de la recta intersección de los planos P y Q.
1.
2.
Determinar las proyecciones y la verdadera magnitud de la distancia entre la traza vertical de la recta intersecciÓn
de ambos planos y el punto A dado.
Puntuación:
Apartado
1:
1,§ Buntoe
pu*t*o
Apartado 2:
1,S
Puntuación máxima:
S,ü Funtas
:ffiipÉ,§ü '..t|i,,,,r.,,,....,',,,,,.,',.,..,.,
t.:j,';i,,.,,,,,
,EJ,EffifiIfi ,'1i*l,,ffSfffi¡glu*emRifin
:.r::::
r
,::
:
litrffii*$¡;l*g¡lffi*tsl,
J,#,,
ti.$¡Í$§..F,tÉ¡Ffffi,E,..ffir,Éin$$$s,q§iÉl*,:figl
,:,:.,,:,.,.,.,,,,:,:.:.:::.,::,::::..,:
l.ri,Ésii
er#n#t.llffiffiF
OPCÚN il
EJERCICIO 10: §ISTEil{A DÉDRrcO.
Dada la proyección vertical del triángulo ABC contenido en el plano verticalde proyección y eleje E {e' - e), ss pide:
Dibujar las nuevas proyecciones del triángulo al realizar un giro alrededor del eje E de amplitud 240o en el sentido
contrario a las agujas del reloj. {240o es igual a 1800 + 60o).
I
I
I
c
I
\
/t'
/
/
I
Puntuación:
Obtención de vértices: 2 puntos
Vistasyocultas: l punto
Puntuación máxima: 3 puntos
opctóN
n
EJERCICIO
o.9
I":
/oí
SISTEMA UÉDRICO.
Conocidos los planos P y Q por sus trazas y las goyeciones del tapecio ABCD, se pide:
1.- Hallar las proyecciones de Ia rccta R, interseccirtn de los planos P y Q.
2.- Determinar las pmyecciones del trapecio ABCD al girarlo 9(}o a[ededor de h recü R, de forma que las nuevas
proyecciones del kapecio sigan estando en el primer cuadrante .
b.o
d
l¿
h
A
'C
Puntuación
Apartado 1: 1.0 puntos
Apartado 2: 2.4 puntos
Puntuación máxima: 3.0 ountos
Opsó1¡il of/06
E.'ERCICNO i :
S§IETA UEDRCO.
p@t
t4ecb¡octárguloABCD €sÉ aofibriloí un pblo B ysesabe quo olsegrnnbabe b
hcrizc¡bl de h base rnayc de didro po[gono, que h ahna BC es igual a 20 mm y que h base rpnor
a 22 mn §e pile dffimhü h poyecc¡ones dáficÉ ddf¿pedo.
Un
CD es
t¡ud
Punü¡acifu.
iPI)
Reprmenhc*in bases:
Represenhción alh¡ra:
Punturción rÉxlma;
2 punbs
1 punto
3
punbs
opcɡru
E,ERGICD to:
os
lo[
§r8rHA OÉOnrO.
tlade la¡ poyeqioms d6 h6 punbs A B y C, se plde;
1. RepesenE h huas d€l plilo P deftúdo por los tes punb§ &d0§.
2. Debm*nr be aryUhs $E ftnm d Éno P mn be plam de ptWitit.
3. De&rmina la veddela nugniüd de h dtra dd tihgulo definklo pa los pufosAB0, ccuiderado
dladoAB.
'|,!
{,
,. ¡!
r*'* ./
+.
\
t
{AJ
iüi
'
i"t¡
Punü.rrcion:
Apartdo 1:
Aparffio 2
AparHo 3:
1,0 puntos
Puntuacién máxima:
3,0 puntos
1,0 punffi
1,0 puntm
como
bas
oPctÓN il
EJERCICIO lo: SlsrEñllA
uÉDRco.
De un plano se conoce su traza horizontal P y su lrazaverticalabatida (P'), asi como elabatimiento delpoligono
ABCD contenido en dicho plano P. Se pide:
1o) Representar latrazavertical del plano P.
20) Representar las proyecciones horizontaly vertical delpoligono ABCD.
P,
Puntuación:
T
¡aza vertical del plano
Proyección horizontal
Proyeccón vertical
Puntuación máxima
1,0 puntos
1,0 puntos
1,0 puntos
3,0 puntos
oP(Ióilt O\/oí
EJERC1CIO
I': SSIHA
TXÉDHCO.
y pforñ*h ve¡tkal o'dd babanto de un
tbda h üaza vsücal de un plaro P perpa|dark al primer tisectÚ h
Hfrgrif €S¡flábrocuúenitoen elphpE ts pila:
1) D#rnin* h taza hod¡onal del pkp P.
polmi&t
qrre ure de *rs vertixo eetá er d phro hoünrral de
ií D"t ;r,ü; hr p,.D".rb,*
"*"r'do
y uno de srs hdoe ea paalelo al pbno tuizonH de guyea*in
*iffit
[i]
Punt¡acit¡n:
lt
0.5 Punbs
Apabdo
2.5 Pnbs
21
Apshdo
Punh¡ación nÉrim¡: 3 Puttbs-
SF§§ÓN
§.§§ftff$$
"t0: slsT§§{A,
§,ÉsRtss"
en dleM plano
Dado el plano F por $us traras, determinar las proy*eci**es de ta circunkre*cia c*ntenida
pr*y*ccién y está situad* en el prim*r §i*drn"
sabiendo que ti*1e tS mm de radia, es tangente a'lox pla*os de
i
zftl
(?t)
Puntua*ión,
Proyección horieuntal:
puntos
Proyec*ién verti**ll
P*ir*tuaei*n rn*xlma:
puntos
§,s suntn*
opcÉilil
a\1oí
EJERGICIO {O: SISTE¡{A DÉDRCO.
a h línea de tienase conocen las poyeccione
De un octogmo regula'ABCDEFGH, cor¡bnirto en un plarn_paralelo
pofiio¡o perunec¡e*es a los¡larm de proyeccitu¡' Se f¡i&
y É ¿e un" O¡rg;ái, ñ',.*'téttu*
¿"
quetunnacor los danosde
¿el pfáñ que cor6ene af omgono, á¡ como los tugulos
ú
n ,ffi ¡
iiO"t"-¡".f*'m"*
pmyecclón.
2) Determinar las poyecciones del odógono.
\i\
\r-* \a,
a\
&
,\
t
Cqo.¡,-¿ia ¡- t
\
Puntuación
:
1.0 puntm
2.0 puntos
Apartado 20 :
Pr¡nt¡reeián márime: 3-0 mlntos
Apartado 10 :
:
)
?"