1.- Calcula el voltaje y la potencia disipada en la resistencia

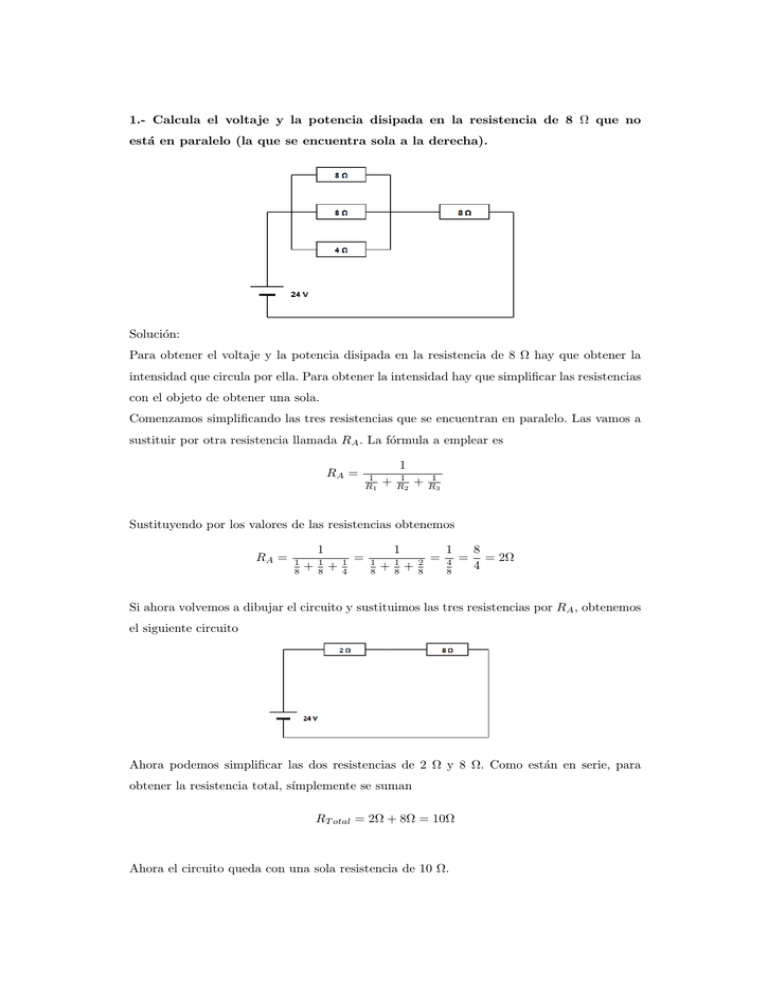
1.- Calcula el voltaje y la potencia disipada en la resistencia de 8 Ω que no
está en paralelo (la que se encuentra sola a la derecha).
Solución:
Para obtener el voltaje y la potencia disipada en la resistencia de 8 Ω hay que obtener la
intensidad que circula por ella. Para obtener la intensidad hay que simplificar las resistencias
con el objeto de obtener una sola.
Comenzamos simplificando las tres resistencias que se encuentran en paralelo. Las vamos a
sustituir por otra resistencia llamada RA . La fórmula a emplear es
RA =
1
1
R1
+
1
R2
+
1
R3
Sustituyendo por los valores de las resistencias obtenemos
RA =
1
1
8
+
1
8
+
1
4
=
1
1
8
+
1
8
+
2
8
=
1
4
8
=
8
= 2Ω
4
Si ahora volvemos a dibujar el circuito y sustituimos las tres resistencias por RA , obtenemos
el siguiente circuito
Ahora podemos simplificar las dos resistencias de 2 Ω y 8 Ω. Como están en serie, para
obtener la resistencia total, sı́mplemente se suman
RT otal = 2Ω + 8Ω = 10Ω
Ahora el circuito queda con una sola resistencia de 10 Ω.
Ya podemos aplicar la Ley de Ohm para obtener el valor de la intensidad
V = I · R −→ I =
V
24V
=
= 2,4A
R
10Ω
Una vez que sabemos el valor de la intensidad, podemos calcular la tensión y la potencia de
la resistencia de 8 Ω. Los datos que tenemos son R = 8Ω e I = 2,5 A. Las fórmulas a utilizar
son V = I · R y P = V · I. Los resultados son
V = I · R = 2,4A · 8Ω = 19,2V
P = V · I = 19,2V · 2,4A = 46,08w
2.- Calcula el voltaje y la potencia disipada en cada una de las resistencias
Solución:
Para obtener el voltaje y la potencia disipada en cada resistencia hay que obtener la intensidad que circula por ella. Para ello simplificamos las resistencias con la intención de dejar el
circuito con una sola resistencia. Al encontrarse las resistencias en serie, la fórmula a aplicar
es RT otal = R1 + R2 + R3 . Si sustituimos los valores tenemos
RT otal = R1 + R2 + R3 −→ RT otal = 10Ω + 20Ω + 30Ω = 60Ω
Si volvemos a dibujar el circuito tenemos
Ahora ya podemos aplicar la Ley de Ohm
V = I · R −→ I =
V
12V
=
= 0,2A
R
60Ω
Al tener la intensidad ya podemos obtener el voltaje y la potencia de cada resistencia. Las
fórmulas a emplear son V = I · R y P = V · I
Para la resistencia de 10 Ω
V = I · R = 0,2A · 10Ω = 2V
P = V · I = 2V · 0,2A = 0,4w
Para la resistencia de 20 Ω
V = I · R = 0,2A · 20Ω = 4V
P = V · I = 4V · 0,2A = 0,8w
Para la resistencia de 30 Ω
V = I · R = 0,2A · 30Ω = 6V
P = V · I = 6V · 0,2A = 1,2w
3.- Simplifica las siguientes resistencias
Solución:
Comezamos simplificando las tres resistencias de 12 Ω, 6 Ω y 4 Ω. Al encontrarse en paralelo
la fórmula a aplicar es
RA =
1
1
R1
+
1
R2
+
1
R3
Sustituyendo por los valores de las resistencias obtenemos
RA =
1
1
12
+
1
6
+
1
4
=
1
1
12
+
2
12
+
3
12
=
1
6
12
=
12
= 2Ω
6
Ahora simplificamos las dos resistencias de 30 Ω y 20 Ω. Al ser sólo dos resistencias, la
fórmula a aplicar es
RB =
R1 · R2
R1 + R2
Sustituyendo por los valores de las resistencias obtenemos
RB =
30Ω · 20Ω
600Ω
=
= 12Ω
30Ω + 20Ω
50Ω
Las resistencias de 12 Ω y 9 Ω al encontrarse en serie se simplifican sumando RC = R1 + R2 .
Sustituyendo sus valores se obtiene
RC = 12Ω + 9Ω = 21Ω
Volviendo a dibujar el circuito tenemos
Ahora podemos simplificar las resistencias de 2 Ω y 12 Ω, que se encuentran en serie. La
fórmula es RD = R1 + R2 . Sustituyendo los valores se obtiene
RC = 2Ω + 12Ω = 14Ω
Si redibujamos otra vez el circuito tenemos dos resistencias de 14 Ω y 21 Ω en paralelo.
que se simplifican con la fórmula
RT otal =
R1 · R2
R1 + R2
Sustituyendo por los valores de las resistencias obtenemos
RT otal =
14Ω · 21Ω
294Ω
=
= 8,4Ω
14Ω + 21Ω
35Ω