EnergeticaSolar
Anuncio

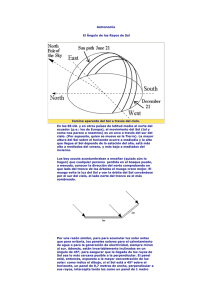
ENERGÉTICA SOLAR Y TRANSMISIÓN DE LA ENERGÍA CONCEPTOS ELEMENTALES DE ASTRONOMÍA EN CUANTO A LA POSICIÓN SOLAR. • • • • • La cantidad de radiación solar que llega a la tierra es inversamente proporcional al cuadrado de la distancia al sol. La distancia media entre la tierra y el sol r0 se denomina UA, Normal a la eclíptica Unidad Astronómica. La tierra de acuerdo con la 1ª ley de Kepler gira en torno al sol N Eje Polar describiendo una órbita elíptica, con el sol situado en uno de sus 23,45º Eje de rotación focos. El eje mayor de la elipse se denomina línea de lo ápsides, siendo sus extremos el perihelio (Tierra más próxima al sol) y el afelio (Tierra más lejos del sol). El plano que contiene la órbita de la tierra se denomina plano de Ecuador la eclíptica. Declinación, ᵹ, ángulo que forma la normal al plano de la eclíptica S con el eje de rotación. 21 Marzo Equinoccio Primavera ᵹ=0º 22 Junio Solsticio Verano ᵹ=23,45º AFELIO 1,017 U.A. PERIHELIO 22 Diciembre Solsticio Invierno ᵹ=-23,45º Focos de la elipse Zona donde no da el sol 0,983 U.A. 23 Septiembre Equinoccio Otoño ᵹ=0º MOVIMIENTOS DE LA TIERRA Movimiento de traslación (1 año sidéreo 236,25636 días) Leyes de Kepler 1º. Ley: Todos los planetas se desplazan alrededor del sol describiendo órbitas elípticas, estando el sol situado en uno de los focos. 2º. Ley: El radiovector que une el planeta y el sol barre áreas iguales en tiempos iguales. (la velocidad varía según la distancia del planeta al sol, más cerca, mayor velocidad) 3º. Ley: Para cualquier planeta, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del sol) es directamente proporcional al cubo de la distancia media con el sol. Adela Valenciano Suárez Página 1 de 12 Movimiento de rotación (1 día 23h 56 min 4,099 s) Este movimiento es la causa de la visibilidad o no (día – noche) del sol desde un determinado lugar de la tierra. Normal a la eclíptica La inclinación del eje de rotación respecto al plano de la eclíptica explica las estaciones (Solsticios de Verano e invierno, equinoccios de primavera y otoño). Esta inclinación hace que en los solsticios (cuando el ángulo entre el plano del ecuador y el plano de la eclíptica es máximo) los rayos de sol incidan más o más verticalmente sobre un hemisferio que en el otro, por eso cuando en un hemisferio es invierno en el otro es verano y al revés. En los equinoccios el ángulo entre el plano del ecuador y el plano de la eclíptica es 0º, los rayos del sol inciden en igual proporción en ambos hemisferios. (Ver imagen b.6. Pag 259 del libro) 23,45º N Eje Polar Eje de rotación Ecuador S Movimiento de precesión: Cambio de dirección en el eje de giro de la Tierra. Se debe al achatamiento de los polos. Movimiento de nutación: Se superpone al movimiento de precesión, de forma que no sean regulares, sino un poco ondulados, los teóricos conos que dibujaría el movimiento de precesión (ver imagen b.7 pag 259, movimiento similar al de una peonza cuando pierde fuerza y está a punto de caerse). Se debe al achatamiento de los polos ya a la atracción de la luna. Adela Valenciano Suárez Página 2 de 12 PLANO DE LA ECLÍPTICA El eje de rotación de la tierra no es perpendicular al plano de la eclíptica. Eso da origen a las estaciones del año. Considerando la tierra en el centro de la elipse y el sol como el que se mueve alrededor de la misma. Podemos definir sobre la órbita terrestre algunos puntos singulares: • • • • Plano del ecuador: Pasa por el centro geométrico del sol y es normal al eje de rotación de la tierra. Plano de la eclíptica: Plano que contiene la órbita de la tierra alrededor del sol. La intersección entre el plano del ecuador y el plano de la eclíptica es la línea de los equinoccios. La línea de los solsticios es perpendicular a la línea de los equinoccios sobre el plano de la eclíptica y pasando por el sol. En los equinoccios el sol se encuentra sobre el plano del ecuador, entonces la duración del día es igual a la de la noche. En los solsticios el sol se encuentra a la máxima inclinación respecto al plano del ecuador (±23,45º), entonces la diferencia entre la duración del día y la noche es máxima. Rotación diaria Bóveda celeste Equinoccio Otoño ᵹ=0º Plano del ecuador Plano de la eclíptica Solsticio Verano ᵹ=23,45º 23,45º -23,45º Solsticio Invierno ᵹ=-23,45º Equinoccio Primavera ᵹ=0º Eje Polar Adela Valenciano Suárez Página 3 de 12 Adela Valenciano Suárez Página 4 de 12 POSICIÓN DE UN OBSERVADOR SOBRE LA SUPERFICIE TERRESTRE A efectos prácticos, aunque la tierra esté achatada por los polos, se puede considerar como una esfera. Sobre ella se definen los siguientes conceptos: Ecuador terrestre: Plano perpendicular al eje de rotación N – S Meridianos: Planos que pasan por los polos y perpendiculares al ecuador. Paralelos: Planos paralelos al ecuador. Un punto cualquiera sobre la superficie terrestre queda determinado por sus coordenadas geométricas, que son: La longitud, λ, ángulo (±180º) medido sobre el ecuador desde el meridiano 0 hasta el meridiano que pasa por el punto, hacia el este positivo, hacia el oeste negativo. La latitud, φ, ángulo (±90º) medido sobre el meridiano que pasa por el punto desde el ecuador hasta el punto, hacia el norte positivo, hacia el sur negativo. NORTE EJE DE ROTACIÓN Punto sobre la superficie terrestre MERIDIANO 0 φ Latitud PLANO DEL ECUADOR OESTE ESTE λ Longitud SUR La inclinación del eje de rotación de la tierra respecto al plano de la eclíptica determina sobre la superficie terrestre unos paralelos denominados trópicos y círculos polares. En verano al mediodía, los rayos solares caen verticalmente sobre el trópico de cáncer. Mientras que en el círculo polar antártico el sol está en el horizonte. En invierno al mediodía, los rayos solares caen verticalmente sobre el trópico de capricornio. Mientras que en el círculo polar ártico el sol está en el horizonte. Esto explica las estaciones. Adela Valenciano Suárez Página 5 de 12 LA ESFERA CELESTE. SISTEMAS DE REFERENCIA. Para determinar la posición de un astro, se considera la esfera celeste. Podemos suponer que la esfera celeste tiene como centro el lugar de observación sobre la superficie terrestre. Para determinar la posición de un astro respecto al lugar de observación, debemos establecer un sistema de referencia: • Sistema de coordenadas celestes horizontales. • Sistema de coordenadas celestes horarias. Sistema de coordenadas celestes horizontales: representa geométricamente el aspecto del cielo visto por un observador situado en un lugar determinado de la superficie terrestre. Se definen los siguientes conceptos: • Plano del horizonte: Plano fundamental. Tangente a la esfera terrestre en el lugar de observación (normal a la línea que marca la plomada). • Horizonte celeste: Círculo máximo (corte) del plano del horizonte sobre la esfera celeste. • Cénit↑ Nadir↓: Puntos donde la normal al plano del horizonte pasando por el observador corta a la esfera celeste. • Círculos verticales: Círculos máximos que pasan por el cénit y nadir, perpendiculares al horizonte. Las coordenadas celestes horizontales de un astro son: • El acimut, Ψ, arco del horizonte celeste comprendido entre el punto cardinal sur y el punto donde el círculo vertical que pasa por el astro corta al horizonte. Se cuenta a partir del sur, de 0º a ±180º, positivamente hacia el oeste y negativamente hacia el este. • La altura, α, arco de dicho círculo vertical comprendido entre el astro y el horizonte. Se mide a partir del horizonte de 0º a 90º, positivamente hacia el cénit y negativamente hacia el nadir. En lugar de la altura α se emplea frecuentemente el ángulo cenital, θz, que es el arco de círculo vertical entre el cenit y el astro. Se cuenta a partir del cénit de 0º a 180º, con lo que la relación entre la altura solar y el ángulo cenital viene dada por: θz=90º- α ESFERA CELESTE CÉNIT θz Ángulo cenital Astro α Altura HORIZONTE CELESTE ESTE NORTE SUR Ψ Acimut OESTE CÍRCULO VERTICAL QUE PASA POR EL ASTRO NADIR Adela Valenciano Suárez Página 6 de 12 Sistema de coordenadas celestes horarias: Basado en el movimiento de rotación de la tierra. Como eje fundamental se adopta el eje de rotación que define sobre la esfera celeste los polos celestes (Norte y Sur) y el ecuador celeste normal al mismo, como círculo máximo fundamental. Se definen los siguientes conceptos: • Círculos horarios o meridianos celestes: círculos máximos que pasan por los polos. • Paralelos celestes: círculos menores paralelos al ecuador • Meridiano superior del lugar: Meridiano o círculo horario que pasa por los polos celestes, el cénit y el nadir. Las coordenadas celestes horarias de un astro son: • El ángulo horario, ω, arco del ecuador celeste comprendido entre el meridiano superior del lugar y el círculo horario que pasa por el astro. • La declinación, ᵹ, arco del círculo horario que pasa por el astro, comprendido entre el ecuador y éste. Astro MERIDIANO SUPERIOR DEL LUGAR CÉNIT ᵹ Declinación POLO NORTE CELESTE HORIZONTE CELESTE ω Ángulo horario ESTE NORTE SUR OESTE MERIDIANO CELESTE O CÍRCULO HORARIO QUE PASA POR EL ASTRO POLO SUR CELESTE ECUADOR CELESTE NADIR El ángulo que forman los planos del horizonte y del ecuador depende de la latitud geográfica del observador. La altura del polo norte celeste sobre el horizonte es igual a la latitud geográfica del observador. El ángulo formado por horizonte y ecuador es el complemento de la latitud geográfica del observador. Las coordenadas celestes horizontales de un astro vienen dadas en función de sus coordenadas celestes horarias y de la latitud del observador. (Ver figura en pag 263 del libro Triángulo de Bessel) Adela Valenciano Suárez Página 7 de 12 Adela Valenciano Suárez Página 8 de 12 MOVIMIENTO APARENTE DEL SOL SOBRE EL HORIZONTE Las coordenadas del sol varían continuamente con el tiempo. Como consecuencia de los movimientos relativos del sol y la tierra. El sol describe en un determinado lugar unas trayectorias dependiendo del día del año, que podemos ver en la figura de la página 265 del libro. La altura máxima del sol (a las 12:00 hora solar) se puede calcular según lo siguiente: h=90-latitud±declinación solar( ) Siendo = 23,45 sin + 284 , donde es la declinación solar y dn es el día juliano (1<=dn<=365) Podemos ver en la gráfica del libro pag 265, o en las siguientes gráficas, como cada día del año el sol sigue una trayectoria cuyas coordenadas acimut y altura vemos representadas en la gráfica. En esta gráfica se puede determinar los intervalos de tiempo y los días en los cuales la instalación solar no recibe radiación solar directa. Determinar las coordenadas solares según: • • • ubicación geográfica: latitud (λ) y longitud (L) día del año (n) hora solar La hora solar debe expresarse en grados, del meridiano celeste del sol respecto a la posición del mediodía. El ángulo horario a las 12:00 h es 0º (donde 1º = 4min y 15º = 60 min). Matemáticamente el ángulo horario se define: Ángulo horario, = 12 − ℎ 9:00 am = 45º 12:00 máxima altura solar mediodía = 0º = 45º ℎ = 45º E 6:00 a.m. orto = 90º 18:00 ocaso = −90º W 24ℎ ∗ 15 El primer paso en el cálculo es determinar la declinación, la cual puede obtenerse a partir de la ecuación de Cooper: = 23,45 sin + 284 , donde es la declinación solar y dn es el día juliano (1<=dn<=365) Las coordenadas solares altura (h) y acimut (z), quedan definidas por las siguientes ecuaciones: Altura solar. Se mide a partir del horizonte de 0º a 90º. Adela Valenciano Suárez Página 9 de 12 #$ ℎ = % #& ∗ % # ∗ % # + #$ & ∗ #$ Acimut solar. Se mide a partir del sur, de 0º a ±180º, positivamente hacia el oeste y negativamente hacia el este. % #' = #$ ℎ ∗ #$ &– #$ % #ℎ ∗ % #& Haciendo uso de las expresiones anteriores puede calcularse la longitud del día (w), es decir, el tiempo de sol desde el orto hasta el ocaso. (Haciendo h=0) ) = 2 ∗ [ %% # −+ & ∗ + ]; Ángulo horario O bien - 2 %.ó $0 í = 3 ; (horas) Mientras que el orto y el ocaso se definen por: Orto: )3 = + %% # + & ∗ + ]; Ángulo horario O bien 4 + = 25 3 ; (horas) Ocaso: )6 = − %% # −+ & ∗ + ]; Ángulo horario O bien 4 + = 27 3 + 12; (horas) Adela Valenciano Suárez Página 10 de 12 POSICIÓN DEL SOL RELATIVA A UNA SUPERFICIE PLANA. Viene caracterizada por los siguientes ángulos que podemos ver representados en la imagen de la pagina 266 del libro. Ángulo de incidencia, θ: ángulo que se forma entre el rayo solar y la normal a la superficie. La pendiente o inclinación, β, ángulo formado por la superficie plana con el plano horizontal (del horizonte) La orientación o acimut del captador, α: ángulo formado por la proyección horizontal de la normal a la superficie, se mide en el plano del horizonte de S a E positivo. Acimut solar, z: Se mide a partir del sur, de 0º a ±180º, positivamente hacia el oeste y negativamente hacia el este. Altura solar, h: Se mide a partir del horizonte de 0º a 90º. La inclinación óptima (más favorable cuando la radiación es perpendicular a la superficie inclinada) para el panel o captador solar será (se ve claramente en la hoja de cálculo): • • • En los equinoccios β=Latitud En el solsticio de verano β=Latitud -23º27’ En el solsticio de invierno β=Latitud +23º27’ Adela Valenciano Suárez Página 11 de 12 En general se toma la inclinación del panel igual a la latitud corregida: • • • β = Latitud+10 para favorecer la captación en invierno β = Latitud-10 para favorecer la captación en verano β = Latitud para un periodo anual Aunque depende también de la climatología del lugar, por ejemplo en Canarias la inclinación óptima de los paneles es de unos 18º, ya que el clima es prácticamente verano todo el año. Para determinar el ángulo de incidencia del rayo solar en relación a cualquier superficie inclinada con un ángulo β respecto al plano horizontal, y una orientación α con respecto al sur, podemos usar la siguiente fórmula: % #8 = % #ℎ ∗ cos ' + ; ∗ #$ < + #$ ℎ ∗ % #< CONVERSIÓN DE LA ENERGÍA SOLAR. La energía solar se convierte de forma directa (captación fotovoltaica, captación térmica) o indirecta (eólica, olas, hidráulica) en otras formas de energía. A efectos prácticos podemos considerar que el sol nos hace llegar a la tierra 1367W/m2 en forma de radiación electromagnética, a este valor se le denomina constante solar. Radiación extraterrestre (constante solar) 1367 W/m2 ±3,3% (según la variación de la distancia tierra sol) De esta energía que nos llega del sol, parte es atenuada por la atmósfera. Una parte se refleja, otra es absorbida por la atmósfera y el resto penetra hacia la superficie de la tierra. Parte de esta última es absorbida o se difunde por el dióxido de carbono, el oxigeno, el ozono y el vapor de agua. De la radiación que nos llega realmente a la tierra las células fotovoltaicas sólo son capaces de utilizar la radiación con longitud de onda comprendida entre los 0,35 y todo el infrarrojo. Por todo lo dicho, la intensidad de radiación ha quedado reducida al valor de 1000W/m2 en lugar de los 1367. Por todo lo dicho, para diseñar sistemas de energía solar es necesaria una caracterización de la radiación disponible bajo diversas condiciones atmosféricas. (Ver figura libro pag 275) La radiación solar global (G) directa que llega a una superficie se divide en tres partes: • Radiación directa (I): Formada por los rayos que proceden del sol directamente. • Radiación difusa (D): procede de toda la bóveda celeste, excepto la que llega del sol. Originada por los efectos de dispersión de los componentes de la atmosfera, incluidas las nubes. • Radiación de albedo (R): Procedente del suelo, reflejada por éste. Al cociente entre la radiación reflejada y la incidente en la superficie de la tierra se le llama albedo. G=I+D+R En la figura de la pag 276 del libro, vemos que: los días despejados se alcanzan niveles de irradiancia altos (800 a 1000W/m2), mientras que los días totalmente nublados sólo se tienen 200W/m2 e incluso menos. Podemos encontrar datos sobre radiación solar por zonas climatológicas en Código técnico de la edificación DB HE4 y DB HE5. Podemos encontrar datos climatológicos en el instituto de meteorología. Otros datos interesantes en Instituto tecnológico de Canarias. Editor Grafcan. Adela Valenciano Suárez Página 12 de 12