Uso de Materiales
Anuncio

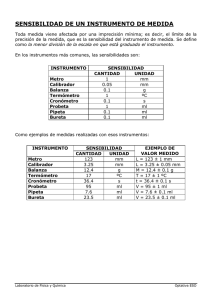
USO DE MATERIALES DE LABORATORIO DETERMINACIÓN DE LA PRECISIÓN Y EXACTITUD DE INSTRUMENTOS PRECISIÓN indica de la reproducibilidad de las medidas realizadas con un mismo instrumento. Se determina a través de la desviación promedio de un conjunto de medidas realizadas siempre con un mismo instrumento. Se expresa con una cifra significativa. USO DE MATERIALES DE LABORATORIO DETERMINACIÓN DE LA PRECISIÓN Y EXACTITUD DE INSTRUMENTOS EXACTITUD indica cuanto se acerca el valor de una medida respecto del valor considerado “verdadero” o “aceptado”. Se determina a través del error absoluto que es la diferencia entre el valor considerado “verdadero” y la medida. USO DE MATERIALES DE LABORATORIO ERROR RELATIVO indica la magnitud o impacto del error en la medida que se está realizando. Se determina a través del cociente entre el error absoluto y el valor considerado “verdadero”. Ej.: si se comete un error absoluto de 1m en la medida de un estadio de fútbol de 100 m, entonces el error relativo es de 1/100 para la medida del estadio. Si se comete un error absoluto de 1m en la medida de la distancia La Plata-Buenos Aires de 100.000 m, entonces el error relativo es de 1/100.000 para la medida de la distancia. USO DE MATERIALES DE LABORATORIO Precisión de una Balanza Granataria Peso objeto (g) promedio (g) desviación indiv (g) 5,5733 5,571566 0,001734 5,5766 5,571566 0,005034 5,5697 5,571566 0,001866 5,5818 5,571566 0,0102340 5,5712 5,571566 0,000366 5,5568 5,571566 0,014766 ecisión PRECISIÓN = 0,006 g a La pr re con un a v p siem ignificati s cifra EXPRESIÓN CORRECTA DEL RESULTADO = (5,572 ± 0,006) g USO DE MATERIALES DE LABORATORIO Exactitud de una Balanza Granataria Peso “aceptado” del objeto = 5,5563 g El valor “verdadero” o “aceptado” de una medida se obtiene con un instrumento más preciso y exacto. Peso promedio = 5,572 g Error absoluto, Ea = | 5,5563 – 5,572 | La exactitud de la balanza granataria es Ea = 0,016 g USO DE MATERIALES DE LABORATORIO Error Relativo de la Medida Error absoluto, Ea = 0,016 g Peso “aceptado” del objeto = 5,5563 g Error relativo, Er %= ( Ea/peso “aceptado”) * 100 Er %= ( 0,016 g/5,5563 g ) * 100 Er % = 0,29 USO DE MATERIALES DE LABORATORIO Precisión de una Balanza de Cadena Peso objeto (g) promedio (g) desviación indiv (g) 6,1225 6,122233 0,000267 6,1220 6,122233 0,000233 6,1222 6,122233 0,000033 6,1211 6,122233 0,001133 6,1218 6,122233 0,000433 6,1238 0,001567 ecisión a La pr re con un a PRECISIÓN = 0,0006 g siemp ignificativ 6,122233 cifra s EXPRESIÓN CORRECTA DEL RESULTADO = (6,1222 ± 0,0006) g USO DE MATERIALES DE LABORATORIO Exactitud de una Balanza de Cadena Peso “aceptado” del objeto = 6,1170 g El valor “verdadero” o “aceptado” de una medida se obtiene con un instrumento más preciso y exacto. Peso promedio = 6,1222 g Error absoluto, Ea = | 6,1170 – 6,1222 | La exactitud de la balanza granataria es Ea = 0,0052 g USO DE MATERIALES DE LABORATORIO Error Relativo de la Medida Error absoluto, Ea = 0,0052 g Peso “aceptado” del objeto = 6,1170 g Error relativo, Er %= ( Ea/peso “aceptado”) * 100 Er %= ( 0,0052 g/6,1170 g ) * 100 Er % = 0,085 USO DE MATERIALES DE LABORATORIO Precisión de distintos materiales utilizados para determinar volúmenes de líquidos Precisión de un vaso de precipitados: ± 1 ml Precisión de una probeta: ± 0,5 ml Precisión de una pipeta graduada: ± 0,06 ml La precisión de la Bureta es ± 0,05 ml Orden creciente de precisión de los instrumentos volumétricos Vaso < probeta < pipeta graduada < bureta USO DE MATERIALES DE LABORATORIO Diámetro del vaso 5,00 cm diámetro de la probeta 2,50 cm diámetro de la pipeta ~ 1,00 cm USO DE MATERIALES DE LABORATORIO 1- A partir de los diámetros del vaso, probeta y pipeta graduada, calcular la variación de altura ∆h que se observará en los distintos instrumentos cuando se vierten 20,00 cm3 de un líquido. 2- Sabiendo que la mínima diferencia de altura que puede observar el ojo humano es de 0,50 mm (error de lectura), calcular el error de los distintos instrumentos. Nota: estos instrumentos son cilíndricos por lo tanto, V = π r2 h USO DE MATERIALES DE LABORATORIO A partir de los diámetros del vaso, probeta y pipeta graduada, calcular la variación de altura ∆h que se observará en los distintos instrumentos cuando se vierten 20,00 cm3 de un líquido. ∆V = π r2 ∆h ∆h = ∆V / π r2 Vaso de precipitados ∆h = 20,00 cm3/ π (2,50)2 cm2 ∆h = 1,01 cm Probeta ∆h = 20,00 cm3/ π (1,25)2 cm2 ∆h = 4,07 cm Pipeta graduada ∆h = 20,00 cm3/ π (0,50)2 cm2 ∆h = 25,5 cm USO DE MATERIALES DE LABORATORIO Sabiendo que la mínima diferencia de altura que puede observar el ojo humano es de 0,50 mm (error de lectura), calcular el error en volumen que se cometerá con los distintos instrumentos. Vaso de precipitados ∆V = π r2 ∆h ∆V = π x (2,50)2 cm2 x 0,050 cm ∆V = 0,98 cm3 Probeta pipeta graduada ∆V = π r2 ∆h ∆V = π x (1,25)2 cm2 x 0,050 cm ∆V = 0,24 cm3 ∆V = π r2 ∆h ∆V = π x (0,25)2 cm2 x 0,050 cm ∆V = 0,0098 cm3 PROPAGACIÓN DE ERRORES EN LA SUMA Y RESTA Suma de los pesos obtenidos en balanza granataria y cadena Peso objeto (g) b. granataria b. cadena suma (g) 4,4374 4,4698 8,9072 4,4242 4,4687 8,8929 4,4247 4,4694 8,8941 4,4026 4,4693 8,8719 4,4375 4,4693 8,9068 Promedio de la suma = 8,89458 g desviación indiv. (g) 0,01262 0,00168 0,00048 0,02268 0,01222 PRECISIÓN = 0,01 g EXPRESIÓN CORRECTA DEL RESULTADO = (8,89 ± 0,01) g PROPAGACIÓN DE ERRORES EN LA SUMA Y RESTA Al sumar y restar, el resultado no puede tener más posiciones decimales que la medición que tiene menos posiciones decimales Peso del objeto en balanza granataria = (4,43 ± 0,01) g Peso del objeto en balanza de cadena = (4,4693 ± 0,0002) g 4,43?? 4,4693 8,8993 g Quimica La Ciencia Central, T. L. Brown, 9na ed., pag.22 PROPAGACIÓN DE ERRORES EN LA SUMA Y RESTA La propagación del error en la suma y la resta es la sumatoria de los errores absolutos de las medidas individuales Peso del objeto en balanza granataria = (4,43 ± 0,01) g Error absoluto, Ea = 0,01 g Peso del objeto en balanza de cadena = (4,4693 ± 0,0002) g Error absoluto, Ea = 0,0328 g Sumatoria de los Ea = 0,01 g + 0,0328 g = 0,04 g PROPAGACIÓN DE ERRORES EN EL PRODUCTO Y COCIENTE Determinación de la Densidad de una solución Peso (g) Volumen (ml) Densidad (g/ml) 18,8255 17,00 1,10738 18,3042 16,65 1,09935 21,1829 19,40 1,09190 20,8534 19,00 1,09755 20,8212 18,95 1,09874 Promedio de la densidad = 1,098984 g desviación indiv. (g) 0,008396 0,000366 0,007084 0,001434 0,000244 PRECISIÓN = 0,004 g EXPRESIÓN CORRECTA DEL RESULTADO = (1,099 ± 0,004) g PROPAGACIÓN DE ERRORES EN EL PRODUCTO Y COCIENTE En las multiplicaciones y divisiones, el resultado debe informarse con el mismo número de cifras significativas que tiene la medición con menos cifras significativas Ej.: se pesan 3,4067 g de hidróxido de sodio y se llevan a un volumen de 20,00 ml. Calcular la concentración molar de la solución con el número de cifras significativas correctas. Nota: solamente las medidas experimentales limitan las c.s. del resultado. El peso molecular posee infinitas cifras significativas y no afecta las c.s. del resultado. Quimica La Ciencia Central, T. L. Brown, 9na ed., pag.22 SENSIBILIDAD DE UN INSTRUMENTO La SENSIBILIDAD es una medida de la respuesta de un instrumento a una perturbación. Se denomina SENSIBILIDAD de un instrumento a la mínima variación de magnitud que puede determinar dicho instrumento. Sensibilidad de una balanza granataria S = 0,025 div/mg Sensibilidad de una balanza de cadena S = 0,5 div/mg SENSIBILIDAD DE LOS TERMÓMETROS Los termómetros más sensibles poseen un capilar de pequeño diámetro y gran volumen de mercurio (bulbo grande) 1-Termómetro con bulbo de gran volumen, S = 0,160 cm/oC 2-Termómetro con bulbo pequeño, S = 0,0933 cm/oC 3- Termómetro largo de capilar fino, S = 0,6329 cm/oC 4- Termómetro corto de capilar grueso, S = 0,0604 cm/oC SENSIBILIDAD DE LOS TERMÓMETROS Una de las consecuencias de los cambios de temperatura que pueden sufrir los materiales, es la dilatación. La dilatación es siempre el cambio de volumen que sufren los materiales por la variación de la temperatura. La dilatación de los líquidos se expresa como: ∆V = Vo ∆T ∆V variación de volumen; , coeficiente de dilatación cúbica; Vo volumen inicial; ∆T, variación de temperatura Por lo tanto, el volumen final del liquido será: Vf = Vo (1 + ∆T) Hg, coef. dilatación cúbica del mercurio = 1,8 10-4 oC-1 Vo el volumen inicial del mercurio es el volumen del bulbo. SENSIBILIDAD DE LOS TERMÓMETROS Cuando se produce una variación de la temperatura, el mercurio varía su volumen alcanzando un Vf. Debido a que está contenido en un capilar cilíndrico, recorrerá mayor distancia cuanto menor sea el radio del capilar ya que, Vf = π r2 h h = Vf / π r2 Vf, volumen final del mercurio; r, radio del capilar; h, longitud recorrida por el mercurio