DINÁMICA MACROECONÓMICA Y LA CURVA DE PHILLIPS BAJO
Anuncio

DINÁMICA MACROECONÓMICA Y L A CURVA
DE PHILLIPS B A J O DIVERSOS SUPUESTOS
SOBRE EL MECANISMO DE AJUSTE SALARIAL
A l e j a n d r o Rodríguez A r a n a *
B a n c o d e México
R e s u m e n : E n un contexto macroeconómlco simple, cuando los salarios nominales
se fijan mediante una regla de indexación basada totalmente en variables del pasado, un choque en alguna variable nominal o real propicia
que el producto y la inflación comiencen a oscilar, a veces en forma
estable y otras de forma explosiva. Si las oscilaciones son estables, en
muchos casos aparece una dinámica peculiar, probablemente compleja,
en donde el producto y la inflación observan ciclos de orden múltiple,
los cuales, a pesar de todo, muestran patrones definidos.
El modelo de este trabajo sugiere que, en contextos más realistas, cambios marginales en ciertas reglas de ajuste de precios podrían generar
hipersensibilidad de las variables macroeconómicas a los parámetros,
así como inestabilidad dinámica.
Abstract:
In a quite simplified model, when nominal wages are completely predetermined, different macroeconomic shocks produce oscillations in output and inflation that can be stable or explosive. If they are stable,
in many cases a peculiar dynamics, perhaps complex, appears, where
output and inflation show cycles of multiple order. Even in those cases
the cycles show well defined patterns.
The
model of this work suggests that in more real contexts marginal
changes in certain rules of price adjustment could generate hyper sensibility of macroeconomic variables to some parameters, as well as dynamic instability.
Clasificación JEL: C610 E32 E37
Fecha
de recepción: SI VIII
2003
Fecha
de aceptación: 16 III 200J,
* Este artículo se escribió cuando era profesor titular de tiempo completo en
la Universidad Iberoamericana. Las opiniones aquí vertidas son responsabilidad
exclusiva del autor, arodrigueza@banxico.org.mx.
181
182
ESTUDIOS ECONÓMICOS
1. Introducción
Los modelos de c u r v a de P h i l l i p s tradicionales ( B l a n c h a r d , 1990;
F r i e d m a n , 1968; P h e l p s 1967, 1970) establecen u n a relación p o s i t i v a y
u n i t a r i a entre l a inflación presente y l a p a s a d a , y u n a relación n e g a t i v a
entre aquélla y l a t a s a de desempleo. C u a n d o esta especificación - q u e
de a l g u n a m a n e r a representa l a oferta agregada en el p l a n o inflacióndesempleo (ver K i n g , 2 0 0 0 ) - se j u n t a c o n u n a d e m a n d a a g r e g a d a
dinámica t r a d i c i o n a l , el resultado es u n equilibrio que converge a
u n a t a s a n a t u r a l de desempleo (ver B l a n c h a r d , 1990).
N o obstante, a u n q u e l a c u r v a de P h i l l i p s t r a d i c i o n a l puede s e r
consistente en ciertos c o n t e x t o s , s u f o r m a podría ser c r i t i c a b l e e n
otros casos. Específicamente, c u a n d o los precios se f o r m a n c o n base
en u n m a r g e n de g a n a n c i a sobre los salarios ( B l a n c h a r d , 1990; Tay¬
lor, 1979 y L . T a y l o r , 1991), y estos están predeterminados - e s d e c i r
se b a s a n exclusivamente en variables d e l pasado (Benassy, 2 0 0 2 ) - l a
f o r m a de l a c u r v a de P h i l l i p s c a m b i a m a r g i n a l m e n t e c o n respecto a l a
t r a d i c i o n a l . A l j u n t a r esta versión m o d i f i c a d a de l a c u r v a de P h i l l i p s
con l a d e m a n d a agregada usual, el c a m b i o en apariencia m e n o r n o
a l t e r a e l estado estacionario d e l sistema, pero m o d i f i c a de m a n e r a
s u s t a n c i a l l a dinámica d e l m i s m o a diversos choques reales y m o n e tarios.
E n el contexto de este t r a b a j o u t i l i z a n d o l a versión m o d i f i c a d a
de l a c u r v a de P h i l l i p s las oscilaciones n u n c a convergen y p u e d e n ser
1
2
3
Esta demanda es la que establece una relación positiva entre el ingreso y
la cantidad real de dinero. Dinámicamente entre el crecimiento del ingreso y la
diferencia entre la tasa de creación de dinero y la inflación, y ha sido utilizada
por diversos autores. Ver, por ejemplo, Fischer (1977), Taylor (1979, 1980), Bean
(1983), Blanchard (1990), Blanchard y Fischer (1989, cap. 10).
1
Recientemente ha habido un fuerte movimiento que ha hecho surgir lo que
se conoce como la nueva curva de Phillips, la cual especifica la inflación actual
en función de las expectativas de inflación futura y de la tasa de desempleo o
el producto. L a especificación surge de la idea de que diversos precios están
invariables por largos períodos y su fijación toma en cuenta cómo se determinan
los precios futuros de otros bienes. Ver King (2000), Gali (2000) y Gali y López
Salido (2001) para una explicación más concreta de este nuevo enfoque. Asimismo,
el enfoque de la curva de Phillips tradicional no se ha abandonado. E n tiempos
relativamente recientes Fair (2000) hace una evaluación econométrica de dicho
enfoque. E n términos teóricos Jadresic (1997, 2001) y Ghezzi (2001) también
analizan los efectos de la indexación atrasada en la formación de la curva de
Phillips.
2
indexa °ón ^ r i a l T t e ñ ^ s X j T p ^
tasas de desempleo^
A J U S T E SALARIAL
183
estacionarias o explosivas, m i e n t r a s que el enfoque t r a d i c i o n a l i m p l i c a
que u n choque m o n e t a r i o o real p r o p i c i a oscilaciones convergentes d e l
p r o d u c t o y l a inflación. Más aún, los patrones dinámicos a l c a n z a n
cierto g r a d o de c o m p l e j i d a d y de acuerdo con el análisis puede h a b e r
ciclos de o r d e n i n f i n i t o . E n ocasiones, cambios marginales de los
parámetros m o d i f i c a n fuertemente l a f o r m a de dichos ciclos.
L a r e a l i d a d es m u c h o más c o m p l e j a que el modelo aquí a n a l i z a d o ,
pero p o r lo m i s m o surge u n cuestionamiento que parece relevante. S i
u n c o n t e x t o t a n s i m p l i f i c a d o presenta t a l s e n s i b i l i d a d dinámica a u n a
modificación p o c o s u s t a n c i a l en a l g u n a regla, ¿no serán tales efectos
todavía más poderosos en u n contexto más realista? Así, los r e s u l t a dos de este t r a b a j o podrían ser i m p o r t a n t e s , n o porque r e p r o d u z c a n
de m a n e r a fehaciente lo que sucede en economías reales, sino p o r q u e
sugieren que en l a r e a l i d a d podría h a b e r u n a g r a n s e n s i b i l i d a d de a l g u nas variables macroeconómicas clave a las reglas de ajuste de salarios
u otros precios ( h i p e r s e n s i b i l i d a d a las reglas). También sugieren que
podría e x i s t i r u n a m u y fuerte s e n s i b i l i d a d de l a producción y otras
variables a cambios marginales e n los parámetros ( h i p e r s e n s i b i l i d a d
a los parámetros).
L a presencia de oscilaciones n o r m a l m e n t e reduce el bienestar con
respecto a situaciones estacionarias, pues el consumo también oscila
alrededor de s u t e n d e n c i a . S i n embargo, u n consumo estable p r o p o r c i o n a m a y o r u t i l i d a d que u n o que está v a r i a n d o , aunque en p r o m e d i o
sean iguales.
E l artículo está compuesto p o r tres secciones. L a p r i m e r a lleva
a c a b o u n análisis dinámico en u n modelo bastante t r a d i c i o n a l de
c u r v a de P h i l l i p s a u m e n t a d a . L a segunda hace lo m i s m o en u n modelo donde se supone que los salarios nominales se fijan exclusivamente
con respecto a variables pasadas. F i n a l m e n t e , l a tercera sección p r o f u n d i z a en algunos aspectos del análisis dinámico de los dos casos
estudiados.
2. Análisis dinámico de u n m o d e l o de c u r v a de P h i l l i p s t r a d i c i o n a l ( m o d e l o I)
L o s dos modelos a a n a l i z a r p a r t e n de u n a ecuación de m a r g e n de
g a n a n c i a sobre los salarios (ver, por ejemplo, B l a n c h a r d (1990) p a r a
u n a explicación sobre las razones de u t i l i z a r esta versión). E l n i v e l
general de precios t o m a l a siguiente f o r m a
Pt = (1 +
r)W
t
(1)
184
ESTUDIOS ECONÓMICOS
D o n d e P es e l n i v e l general de precios y r el m a r g e n de g a n a n c i a .
P o r simplificación se supone que el coeficiente técnico entre e l t r a b a j o
y el p r o d u c t o es u n o . E s t o i m p l i c a que l a p r o d u c t i v i d a d d e l t r a b a j o
es constante.
L a ecuación anterior llevada a términos logarítmicos, y s i el m a r gen de g a n a n c i a es relativamente pequeño, d a como r e s u l t a d o
P t
=
T
+ w
(2)
t
D o n d e las variables en minúscula son el l o g a r i t m o de las variables
en mayúscula y a definidas.
P o r o t r a p a r t e e l salario n o m i n a l se d e t e r m i n a de l a siguiente
forma
w
t
= p t - i + n t - i + Sy
(3)
t
D o n d e w es el l o g a r i t m o d e l salario n o m i n a l y y el l o g a r i t m o de
l a producción t o t a l de l a economía.
L a ecuación (3) está c o m p u e s t a de dos partes. L a p r i m e r a q u e
es p t - i + T T t - i i n d i c a que, d a d o u n n i v e l de ingreso constante, l a i n dexación a t r a s a d a de los salarios nominales protege a l salario r e a l
c o n t r a cambios en el n i v e l de precios (por el p _ { ) y de l a t a s a de
inflación (por el 7 r , _ i ) . S i estos llegaran a o c u r r i r , l a p o s t e r i o r e s t a b i lización de l a inflación en u n valor constante haría que e l salario r e a l
t o m a r a u n valor independiente de d i c h a inflación.
L a s e g u n d a p a r t e de l a ecuación (3) i n d i c a que m i e n t r a s m a y o r
sea e l n i v e l de producción de l a economía, mayor será el p o d e r de
negociación de los sindicatos p a r a a u m e n t a r salarios nominales. E s t o
es así, p o r q u e c o m o el p r o d u c t o depende p o s i t i v a m e n t e d e l e m p l e o ,
u n i n c r e m e n t o de aquél c o n u n a fuerza de t r a b a j o d a d a i m p l i c a u n a
reducción de l a t a s a de desempleo. C o n menor t r a b a j o d i s p o n i b l e p a r a
u t i l i z a r , los sindicatos pueden incrementar sus d e m a n d a s salariales.
E l parámetro 6 es u n i n d i c a d o r que varía de f o r m a inversa c o n
el p o d e r monopólico de los sindicatos. S i 6 es cero, habrá u n g r a n
p o d e r monopólico porque los líderes de los trabajadores podrán fijar
el salario n o m i n a l independientemente de cuál sea l a tasa de d e s e m pleo. S i p o r e l c o n t r a r i o 6 es inmensamente grande, el p r o d u c t o y e l
desempleo se convertirán e n parámetros d e l modelo y los s i n d i c a t o s
no tendrán ningún p o d e r p a r a fijar salarios nominales.
t
4
Diversos estudios recientes analizan los efectos macroeconómicos de la indexación atrasada. Ver, por ejemplo, Calvo y Vegh (1994), Crowley (1997), Ghezzi
(2001), Jadresic (2001).
4
185
AJUSTE SALARIAL
A l restar e l l o g a r i t m o d e l n i v e l de precios de ambos l a d o s de l a
ecuación (3) se obtiene
W
- P t =
t
TTl-l
-
*"t +
(4)
h t
E s t a ecuación c o n f i r m a lo d i c h o c o n a n t e r i o r i d a d : c u a n d o l a i n flación t o m a u n valor constante, e l salario r e a l dependerá sólo d e l
ingreso.
L a ecuación (3) es c o m p a t i b l e c o n l a c u r v a de salarios de B l a n c h flower y O s w a l d (1994). E l salario n o m i n a l depende en f o r m a n e g a t i v a
de u n a referencia de precios y de l a t a s a de desempleo. B l a n c h a r d
(1990) p r e s e n t a u n a formación de salarios c o m p a t i b l e c o n l a c u r v a
de P h i l l i p s de M i l t o n F r i e d m a n y E d m u n d P h e l p s ( F r i e d m a n , 1968;
P h e l p s , 1967, 1970). N o obstante, B l a n c h a r d y Pérez E n r r i (2000,
caps. 15 a l 17. E n especial l a página 332 e x p l i c a l a especificación
de l a ecuación de salarios) m u e s t r a n u n a determinación de salarios
s i m i l a r a l a aquí r e f e r i d a .
L a diferencia entre l a especificación de salarios c o m p a t i b l e c o n
B l a n c h f l o w e r y O s w a l d y l a de F r i e d m a n y P h e l p s es que, e n l a p r i m e r a
l a t a s a de g a n a n c i a q u e d a directamente r e l a c i o n a d a c o n l a inflación
contemporánea, m i e n t r a s que e n l a segunda l a t a s a de g a n a n c i a se
e l i m i n a de l a c u r v a de P h i l l i p s de precios.
S u s t i t u i m o s (3) e n (2) y se o b t i e n e
5
6
7
Tt =
T + • K t - i + Syt,
(5)
que es u n a c u r v a de P h i l l i p s a u m e n t a d a t r a d i c i o n a l . D i c h a función
presenta u n coeficiente u n i t a r i o p a r a l a inflación pasada. S i en e l largo
plazo l a inflación es constante, el p r o d u c t o no depende de d i c h a tasa.
Blanchard (1990) presenta una forma funcional donde el cambio en el salario
nominal depende positivamente de la inflación atrasada y del ingreso. E l resultado
en términos cualitativos será una curva de Phillips muy similar a la aquí obtenida,
sólo que en el caso de Blanchard la inflación no depende de la magnitud de la tasa
de ganancia y en este caso sí.
5
Existe una fuerte controversia sobre si los salarios se forman de la manera
descrita por Friedman y Phelps, o si se forman como Blanchflower y Oswald
sugieren. Roberts (1997) muestra que bajo un contexto de contratos de salarios
traslapados ambas visiones pueden ser compatibles.
6
Si se toma la visión de Friedman y Phelps, entonces W - W - \ = » r _ i +
Sy y, por lo tanto, si utilizamos la ecuación (1) la curva de Phillips en precios
queda especificada como: n = n - l + 6y . Cambios en la tasa de ganancia
afectan el nivel de precios pero no el de inflación.
7
t
t
t
t
t
t
t
186
ESTUDIOS ECONÓMICOS
P o r l o m i s m o , r e s u l t a inútil u t i l i z a r l a política m o n e t a r i a p a r a i n c r e m e n t a r l o y puede decirse que existe u n a t a s a n a t u r a l de d e s e m p l e o .
P o r el lado de l a d e m a n d a agregada el supuesto v a a ser, prácticamente, idéntico a l u t i l i z a d o p o r m u y diversos autores (ver T a y l o r ,
1979, 1980; F i s c h e r , 1977, B l a n c h a r d , 1990 y B l a n c h a r d y F i s c h e r ,
1989, c a p . 10, p. 518). L a d e m a n d a agregada depende d e m a n e r a
p o s i t i v a de l a c a n t i d a d real de dinero. E n este caso s u p o n d r e m o s
también u n a e l a s t i c i d a d u n i t a r i a , que es el caso a n a l i z a d o p o r B l a n c h a r d y F i s c h e r (1989), F i s c h e r (1977) y T a y l o r (1979, 1980). O t r o s
autores como B e a n (1983) y B l a n c h a r d (1990) c o n s i d e r a n casos en
que l a e l a s t i c i d a d es d i s t i n t a de u n o .
8
9
Vt = m + V ( t ) - p
t
t
(6)
E s t a es u n a ecuación de d e m a n d a agregada d i r e c t a m e n t e r e l a c i o n a d a c o n l a teoría c u a n t i t a t i v a d e l dinero. L a d e m a n d a t o t a l p o r
ingreso está r e l a c i o n a d a de m a n e r a p o s i t i v a c o n l a c a n t i d a d de d i n e r o
m y c o n l a v e l o c i d a d de circulación d e l dinero V, y de f o r m a n e g a t i v a
con e l n i v e l general de precios.
U n supuesto a d i c i o n a l será que l a v e l o c i d a d de circulación d e l
dinero crece e n el t i e m p o , lo c u a l es razonable. E n décadas recientes
h a h a b i d o grandes cambios tecnológicos en el sector financiero y l a
d e m a n d a de dinero h a tendido a caer, incrementándose l a v e l o c i d a d .
P a r a simplificar lo antes descrito, el supuesto será que l a v e l o c i d a d de circulación d e l dinero se c o m p o r t a en el t i e m p o en f o r m a
lineal:
V = vt
(7)
D o n d e v es u n a constante.
S i restamos (6) de s u rezago y arreglamos términos se llega a
Este supuesto surge por la especificación de la ecuación de salarios que
supone indexación perfecta. Si la indexación sobre la inflación no fuera perfecta, de modo que w = P t - 1 + P ^ t - l + % donde 0 < 1, la curva de
Phillips sobre precios sería 7T< = r + 0 n - i + óljt, y habría una sustitución de
largo plazo (trade
off) entre inflación y desempleo. Diversos autores han encontrado empíricamente una sustitución de largo plazo entre inflación y desempleo
en Estados Unidos (Gordon, 1972; Brainard y Perry, 2000 y Fair, 2000). A nivel
teórico Akerlof, Dickens y Perry (1996, 2000) han estudiado porqué podría haber
una sustitución de largo plazo entre inflación y desempleo.
8
t
t
9
Una elasticidad unitaria de la demanda de ingreso con respecto a la cantidad
real de dinero es una versión de la teoría cuantitativa del dinero.
187
AJUSTE SALARIAL
(8)
Dt ~ V t - x = f i - ir + v
t
H es l a t a s a de creación de d i n e r o , l a c u a l se supone constante.
E l s i s t e m a de ecuaciones en diferencias que resuelven p a r a l a
inflación y el p r o d u c t o q u e d a conformado p o r las ecuaciones (5) y (8)
y se repite p o r conveniencia:
7T
t
= 7T _l + 6 y
t
y t - y t - i = —itt
T
(9)
+ T
(10)
+1¿ + v
E n corto p l a z o (en el m o m e n t o t) este sistema resuelve p a r a e l
valor p u n t u a l de l a inflación y el p r o d u c t o . E n largo p l a z o el s i s t e m a
resuelve p a r a l a t r a y e c t o r i a de ambas variables. E l s i s t e m a d e b e resp o n d e r c ó m o ante perturbaciones monetarias (cambios e n / i o « ) o
reales (cambios en r o 6) se afectan l a inflación y el p r o d u c t o en e l
corto p l a z o (en í) y e n s u t r a y e c t o r i a de largo plazo.
2.1. Solución
constante
del modelo I cuando
la t a s a d e creación
monetaria
es
E l m o d e l o I, representado p o r las ecuaciones (9) y (10) en s u f o r m a
e s t r u c t u r a l , puede representarse en su f o r m a r e d u c i d a de c o r t o p l a z o
c o m o u n vector autorregresivo de las variables ir y y
1
TTt —
1 + 6
1
1+6
~ t - i
n
Vt =
La
1
(M + " )
1+ 6
, Vt-i
, H
1
1
(11)
1+6
+
V
-
T
(12)
1+6
1+ 6
1+ 6
solución de estado estacionario de este modelo ir = i r - i
t
y
t
Vt = 2 / t - i es:
»t = - J
( )
ir = p + v
(14)
t
1 3
E n e l estado estacionario el p r o d u c t o depende negativamente de
los dos poderes monopólicos de l a economía: el de los empresarios,
representado p o r el m a r g e n de g a n a n c i a T , y el de los t r a b a j a d o r e s
188
ESTUDIOS ECONÓMICOS
representado p o r ( 1 / 6 ) . L o s choques monetarios no t i e n e n efecto sobre el p r o d u c t o d e l estado estable.
L a solución e s t a c i o n a r i a también i n d i c a que l a inflación es u n
fenómeno p u r a m e n t e m o n e t a r i o , y no depende de los poderes m o n o p ó licos de t r a b a j a d o r e s y empresarios. E s t a visión c o n t r a s t a con l a
s o s t e n i d a por las escuelas post-keynesiana y e s t r u c t u r a l i s t a (ver D e sai, 1973; R o w t h o r n , 1977 y L . T a y l o r , 1 9 9 1 ) .
N o obstante, e l
r e s u l t a d o es válido sólo p a r a el estado estacionario.
L a p r e g u n t a a contestar a h o r a es: ¿de qué m a n e r a u n c h o q u e
m o n e t a r i o o real a l t e r a el e q u i l i b r i o de corto y largo p l a z o de l a
economía? E l ejercicio supondrá que antes d e l choque l a t a s a de
creación de d i n e r o es constante. U n a vez que el choque tiene l u g a r
sigue siendo constante.
U n a p r i m e r a f o r m a de contestar lo anterior resulta de i n v e s t i g a r
las raíces características del m o d e l o en su f o r m a r e d u c i d a (ecuaciones
(11) y (12)). C u a n d o dichas raíces son menores que l a u n i d a d , e l
modelo converge en el largo plazo a u n nuevo estado estacionario. S i
además dichas raíces son complejas, habrá oscilaciones en las p r i n c i pales variables de l a economía.
L a s raíces características del s i s t e m a (11) y (12) son:
10
—
T ^ u S p
('»)
C o m o 6 es u n valor siempre p o s i t i v o , las raíces son siempre c o m plejas y pueden representarse de l a siguiente f o r m a
± -,
rj2=
r i ,
(16)
1 + 6
(1 + 6)
donde i es l a raíz c u a d r a d a de - 1 , que es u n número i m a g i n a r i o .
P a r a saber si existen raíces u n i t a r i a s es necesario evaluar l a raíz
c u a d r a d a de l a s u m a del p r i m e r término de (16) y d e l término que
m u l t i p l i c a al número i (ver por ejemplo C h i a n g , 1984, cap. 15, p.
513). E n este caso el valor de l a s u m a m e n c i o n a d a es:
1
(1+6) /
1
2
< 1
(17)
En particular L. Taylor (1991 p. 87) supone un mecanismo de indexación
salarial similar al aquí expresado, y encuentra que la inflación puede depender
del conflicto distributivo entre los patrones que imponen una tasa de ganancia y
los trabajadores que indexan sus salarios hacia atrás. Un mecanismo similar fue
estudiado con anterioridad por Modigliani y Padoa- Shioppa (1978)
1 0
A J U S T E SALARIAL
189
E l v a l o r es m e n o r que u n o pues 6 siempre es m a y o r que cero.
L o a n t e r i o r i m p l i c a q u e el m o d e l o formado p o r las ecuaciones (11) y
(12) tiene raíces menores que l a u n i d a d y converge a l e q u i l i b r i o e s t a c i o n a r i o . Más aún, c o m o las raíces representadas e n (16) son c o m p l e jas, el m o d e l o desplegará siempre oscilaciones convergentes alrededor
del estado estacionario.
E l v a l o r de 6 i n d i c a de que m a n e r a se d a n las oscilaciones. S i
6 es m u y pequeña, casi t e n d i e n d o a cero, l a ecuación (17) m u e s t r a
que el v a l o r 1/(1 + 6 ) ' es m e n o r pero m u y cercano a u n o . E n este
caso, e l m o d e l o casi presenta raíces u n i t a r i a s y e l e q u i l i b r i o converge,
pero de f o r m a l e n t a c o n grandes oscilaciones. E n c a m b i o , c u a n d o
6 es m u y grande e l m o d e l o está m u y lejos de las raíces u n i t a r i a s y
l a convergencia a l e q u i l i b r i o estacionario también es o s c i l a t o r i a p e r o
más rápida.
E l r e s u l t a d o anterior tiene g r a n i m p o r t a n c i a desde e l p u n t o de
v i s t a económico. 6 es u n valor inversamente relacionado c o n e l p o d e r
monopólico de los trabajadores. C u a n d o dicho p o d e r es m u y grande,
l a s a l i d a d e l e q u i l i b r i o producirá u n ajuste más lento que si e l m e r cado de t r a b a j o fuera más c o m p e t i t i v o . L a m a y o r c a n t i d a d de ciclos
p r o n u n c i a d o s p o r l a f a l t a de c o m p e t e n c i a tendrá, m u y posiblemente,
u n efecto negativo en el bienestar de l a sociedad (ver P o o l e , 1970;
B e a n , 1983 o T a y l o r , 1979, 1980, p a r a u n análisis de ciclos y bienestar social).
E n este m o d e l o l a t a s a de g a n a n c i a T no tiene u n a i n f l u e n c i a
en l a f o r m a que t o m a n las oscilaciones, pero sí influye en e l valor
que finalmente tiene l a p r o d u c c i ó n .
A s u vez, e l poder monopólico
de los sindicatos influye t a n t o en l a dinámica c o m o e n e l v a l o r de
e q u i l i b r i o de l a producción. Desde e l p u n t o de v i s t a económico habría
que c o m b a t i r ambos poderes monopólicos. N o obstante, s i el o b j e t i v o
fuera r e d u c i r el t i e m p o de ajuste a l e q u i l i b r i o habría p r i m e r o que
i n c r e m e n t a r l a c o m p e t e n c i a e n e l mercado de t r a b a j o .
A l p a r t i r de u n estado estacionario, u n a u m e n t o e n l a t a s a de
creación de dinero o de l a t r a y e c t o r i a de s u v e l o c i d a d de circulación
tendría, e n p r i m e r a i n s t a n c i a , u n efecto p o s i t i v o sobre l a producción y
l a t a s a de inflación, lo c u a l puede observarse e n las formas reducidas
de corto p l a z o (11) y (12). Después de ese i m p a c t o , l a economía
0
5
11
Este resultado surge porque la tasa de ganancia es constante. Sin embargo,
hay modelos donde la tasa de ganancia depende del ingreso, algunas veces en
forma positiva como lo sugiere L . Taylor (1991, p. 87) o negativa, como es el
caso propuesto por Romer (1996, cap. 5). Ambos autores, no obstante, también
consideran el caso en el que la tasa de ganancia es independiente del nivel de
producción.
1 1
190
ESTUDIOS ECONÓMICOS
convergiría e n f o r m a cíclica a l nuevo estado estacionario, d o n d e l a
inflación sería m a y o r y l a producción igual a l a i n i c i a l . C o m o el
e q u i l i b r i o es cíclico, habría continuas recesiones y expansiones, a u n q u e
menos p r o n u n c i a d a s conforme p a s a el t i e m p o .
P o r o t r a p a r t e , u n a u m e n t o en l a tasa de g a n a n c i a r tendría, e n
u n p r i m e r m o m e n t o , u n efecto negativo sobre el p r o d u c t o y p o s i t i v o
sobre l a inflación (ver ecuaciones (11) y (12)). E n el largo p l a z o el p r o d u c t o caería y l a inflación volvería a ser i g u a l a ¿t + v. E n este p u n t o
surge u n a p a r c i a l reconciliación de este enfoque c o n e l e s t r u c t u r a l i s t a
o post-keynesiano: u n a economía que se vuelve más monopólica, efect i v a m e n t e , presenta u n período donde l a inflación p r o m e d i o es m a y o r
que sus fundamentos m o n e t a r i o s , y a que e l p r o d u c t o p r o m e d i o está
cayendo.
12
3. A n á l i s i s d i n á m i c o d e u n m o d e l o d o n d e l o s s a l a r i o s n o m i n a l e s s e fijan s ó l o c o n b a s e e n v a r i a b l e s r e t r a s a d a s ( m o d e l o
Versiones m u y similares a l m o d e l o I h a n sido u t i l i z a d a s p a r a e x p l i c a r
el ciclo económico. C o n supuestos diferentes a los aquí expuestos
el m o d e l o podría todavía seguir siendo útil. P o r e j e m p l o , si h a y
r e n d i m i e n t o s decrecientes en el factor t r a b a j o y l a indexación s a l a r i a l
no i n c l u y e el ingreso presente - e s decir, h a y t o t a l p o d e r m o n o p ó l i c o
de los s i n d i c a t o s - el m o d e l o resultante es u n a versión m u y p a r e c i d a a
l a e x p u e s t a e n este t r a b a j o . También el e q u i l i b r i o sería convergente
y s i e m p r e exhibiría o s c i l a c i o n e s .
E s p r o b a b l e que el p o d e r monopólico de los sindicatos esté s i e m pre l i m i t a d o p o r l a m a g n i t u d d e l p r o d u c t o y de l a t a s a de desempleo,
p o r lo que parece recomendable i n c l u i r l a producción o e l desempleo
1 3
14
Sin embargo, debido a la trayectoria oscilatoria de las variables económicas
habría ciertos momentos en la transición en que la inflación caería por debajo de
sus fundamentos monetarios.
í ¿
Versiones donde la regla salarial no incluye la tasa de desempleo o el ingreso han sido propuestas por Fischer (1977) y Gray (1976). Estas trabajan con
rendimientos decrecientes en el factor trabajo y en ellas se observa una relación
negativa entre el producto y el salario real, lo que ha sido criticado por diversos
autores (ver Blanchard, 1990 y Romer, 1996).
1 3
Blanchard (1990) afirma que cuando la cantidad de dinero aumenta de una
vez por todas el modelo puede o no exhibir oscilaciones. Este artículo muestra,
no obstante, que cuando hay cambios en la tasa de creación de dinero el modelo
siempre exhibe oscilaciones.
1 4
A J U S T E SALARIAL
191
en l a ecuación de salarios. S i n embargo, c u a n d o hay u n e s q u e m a p a r c i a l o t o t a l de indexación a t r a s a d a , l a inclusión de l a producción e n
l a f o r m a e n que se llevó a cabo en l a sección anterior - y en o t r o s t r a b a j o s - puede contener u n a contradicción. L a explicación se e x p o n e
a continuación.
1 5
S i los salarios n o m i n a l e s se fijan d u r a n t e el período e n cuestión,
p o r ejemplo en í, n o deberían contener u n elemento de indexación
a t r a s a d a , y a que los precios de d i c h o período son observables. D e este
m o d o , los salarios n o m i n a l e s pueden buscar u n a referencia r e a l d i r e c t a m e n t e e n los precios d e l período t . P a r a que l a indexación a t r a s a d a
tenga sentido es necesario suponer que los salarios que prevalecerán
e n t se fijan antes de q u e comience d i c h o período.
D e acuerdo c o n l o anterior, s i los salarios se fijan antes de t,
entonces e l ingreso e n t no puede ser uno de sus argumentos, p o r q u e n o
es observable e n e l m o m e n t o de l a fijación. E n t o d o caso, l a referencia
tendría q u e ser u n a e x p e c t a t i v a de ingreso, pero s i así fuera, e n lugar
de l a indexación a t r a s a d a también debería haber u n esquema donde
los salarios se fijaran en relación c o n u n a e x p e c t a t i v a de precios.
Podría a r g u m e n t a r s e que los salarios n o m i n a l e s t i e n e n dos partes,
u n a fija q u e se c o n t r a t a antes de t , que consiste en l a indexación
a t r a s a d a , y u n a móvil que se d a d u r a n t e t, que está r e l a c i o n a d a c o n e l
ingreso observado e n ese período (por ejemplo, bonos de actuación).
S i n embargo, esta práctica también podría criticarse c o n u n a r g u m e n t o lógico: s i los salarios nominales p u e d e n modificarse p o r el
ingreso observado, también deberían p o d e r hacerlo p o r los precios
observados. S i t a l fuera el caso, el ajuste también debería i n c l u i r l a
parte de los salarios que está i n d e x a d a h a c i a atrás.
Diversos autores (ver F i s c h e r , 1977 y Benassy, 2002) e x a m i n a n
ejemplos e n los cuales los salarios n o m i n a l e s están p r e d e t e r m i n a d o s .
S i t o m a m o s este caso, n o es lógico suponer que en l a ecuación de
salarios e n t i n t e r v e n g a e l ingreso presente, parece más r a z o n a b l e i n c l u i r e l ingreso pasado. E s t e a r g u m e n t o c o b r a relevancia p o r q u e e l
p o d e r de los s i n d i c a t o s se ejerce e n e l m o m e n t o de establecer salarios
y ese p o d e r está r e l a c i o n a d o c o n e l ingreso de t-í, n o c o n e l ingreso
de í. D e m o d o que u n c a m b i o m u y p l a u s i b l e de l a regla s a l a r i a l sería
el s i g u i e n t e :
16
1 5
Tobin (1972), Gordon (1972), Blanchard (1990).
E n un estudio empírico de la curva de Phillips para Estados Unidos, Akerlof,
Dickens y Perry (2000) hacen depender la inflación presente, no sólo del desempleo
en el presente sino también de los valores de la tasa de desempleo de períodos
pasados.
1 6
192
ESTUDIOS ECONÓMICOS
w
(18)
= p t - i + irt-i + 6yt-i
t
E s t e c a m b i o parece menor. E n lugar de que los salarios n o m i n a l e s
d e p e n d a n de los precios del pasado y d e l ingreso presente, a h o r a lo
hacen d e l ingreso pasado, lo que coincide c o n el m o m e n t o en que se
fijan.
No o b s t a n t e , el resultado mostrará que l a dinámica c a m b i a
r a d i c a l m e n t e c o n respecto a l caso a n t e r i o r .
L a ecuación (18) a h o r a se sustituye en l a (2), p o r lo que l a c u r v a
de P h i l l i p s t o m a l a f o r m a
17
7r
f
=
T +
7T _i
+
t
(19)
Syt-i
L a d e m a n d a agregada dinámica es l a m i s m a que l a e x p r e s a d a en
la ecuación (8).
3.1.
Solución
constante
d e l m o d e l o I I c u a n d o la t a s a d e creación
de dinero
es
E l s i s t e m a de l a c u r v a de P h i l l i p s (19) c o n l a d e m a n d a agregada (8)
en f o r m a r e d u c i d a q u e d a c o m o
TT¿
Vt =
— T t - l
=
7Tt_i +
+
6y -i + r
t
(1 — 6 ) y t - i +
(¿t
+
v —
T
E l m o d e l o representado por (20) y (21) tiene u n estado e s t a c i o n a r i o idéntico a l m o d e l o I y expresado en las ecuaciones (13) y
(14). E n d i c h a situación, el p r o d u c t o depende negativamente de los
dos poderes monopólicos del modelo. P o r su parte, l a inflación es
i g u a l a l a tasa de creación de dinero, más el a u m e n t o sistemático e n
la v e l o c i d a d de circulación d e l m i s m o .
Las raíces características de este m o d e l o son:
n,2 =
2
( )
2 2
E n este caso habrá raíces complejas c u a n d o 6 sea m e n o r que 4 y
raíces reales c u a n d o 6 sea igual o mayor que 4.
1 1
Muy recientemente Benassy (2002) ha estudiado el efecto que tienen los
salarios que se fijan por adelantado en el diseño de la política económica.
A J U S T E SALARIAL
193
C u a n d o 6 es m e n o r que 4, el criterio p a r a saber si hay o n o raíces
u n i t a r i a s es e l siguiente
((1- ^) +
2
(
4
~
( 2
4
~
¿ ) 2 )
)
< 1
1 / 2
(23)
Sin embargo, a l desarrollar l a operación en el paréntesis r e s u l t a
que es e x a c t a m e n t e i g u a l a l a u n i d a d . E s t o i m p l i c a que, c u a n d o h a y
un p o d e r monopólico de los t r a b a j a d o r e s r e l a t i v a m e n t e elevado e l
m o d e l o tiene raíces u n i t a r i a s y no converge a l estado estacionario.
C u a n d o hay raíces reales (6 > 4), el criterio p a r a s a b e r si e l
m o d e l o n o converge es que, c u a n d o menos, a l g u n a de las raíces sea
m a y o r o i g u a l a la u n i d a d . L a ecuación (22) m u e s t r a c l a r a m e n t e que
si 6 es e x a c t a m e n t e i g u a l a 4 las raíces son repetidas e iguales a menos
uno, p o r lo que, de nuevo, h a y raíces u n i t a r i a s . S i 6 es e s t r i c t a m e n t e
m a y o r que 4, entonces:
p . ' j . ^ ^ B ^ . ,
(24)
L o que i m p l i c a que, a l menos, u n a de las raíces es e n v a l o r a b soluto m a y o r que l a u n i d a d y el m o d e l o n o convergirá, antes b i e n
divergirá d e l e q u i l i b r i o .
U n c a m b i o p l a u s i b l e en u n o de los supuestos d e l m o d e l o convierte
a este último en inestable. A s i m i s m o , surge u n a conclusión diame¬
t r a l m e n t e opuesta a l a d e l caso anterior: si e l m e r c a d o de t r a b a j o
se vuelve más c o m p e t i t i v o es posible que e l modelo sea todavía más
inestable.
C o n objeto de a n a l i z a r c ó m o serían las soluciones aquí d e s c r i t a s ,
se llevaron a cabo varias simulaciones de las ecuaciones de l a f o r m a
r e d u c i d a (20) y (21). E l c u a d r o 1 m u e s t r a los supuestos de las s i m u laciones.
Cuadro 1
S u p u e s t o s d e las s i m u l a c i o n e s del m o d e l o I I
1
2
3
5
4
6
0.5
2.5
3.8
4.0
4.1
T
0.5
0.5
0.5
0.5
0.5
Mo
0.3
0.3
0.3
0.3
0.3
V
0.0
0.0
0.0
0.0
0.0
(¿
0.5
0.5
0.5
0.5
0.5
194
ESTUDIOS ECONÓMICOS
Cuadro 1
(continuación)
1
2
3
4
5
Tro
0.3
0.3
0.3
0.3
0.3
yo
-1.0
-0.2
-0.135
-0.125
-0.122
L a s simulaciones s u p o n e n que l a economía se e n c u e n t r a en u n
estado estacionario donde l a inflación es 3 0 % , a l i g u a l que el i n c r e mento en l a c a n t i d a d de d i n e r o . E l e x p e r i m e n t o consiste en generar
u n a perturbación en d i c h a t a s a (n), l a c u a l a u m e n t a a 5 0 % . L o s r e s u l tados p a r a el l o g a r i t m o d e l p r o d u c t o de c a d a u n a de las s i m u l a c i o n e s
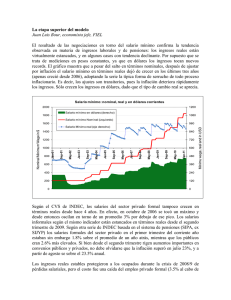
pueden observarse en las siguientes gráficas.
S i m u l a c i o n e s d e l n i v e l del l o g a r i t m o del p r o d u c t o ante
u n a perturbación en la tasa de creación de d i n e r o
Gráfica 1
Simulación 1 . 6 = 0 . 5
Serie 1
Gráñca 3
Simulación 3. 6 = 3.8
A J U S T E SALARIAL
197
C u a n d o 8 es 0.5 las oscilaciones son regulares y estables, pero e l
modelo n u n c a converge de nuevo a l e q u i l i b r i o , sino que flota a l r e d e d o r
de él. M i e n t r a s 8 es m e n o r que 4 e l m o d e l o sigue flotando a l r e d e d o r
del e q u i l i b r i o s i n convergir, pero las oscilaciones y a n o son s i e m p r e t a n
regulares. P o r ejemplo, si 6 = 2.5 los ciclos que se f o r m a n p a r e c e n
de o r d e n 8. L o m i s m o sucede c u a n d o 6 = 3.8. L a i r r e g u l a r i d a d a l
interior de c a d a g r u p o parece estar r e l a c i o n a d a con el hecho d e que 8
t o m e valores n o enteros (ver siguiente sección y apéndice).
E l m o d e l o c o m i e n z a a d i v e r g i r c u a n d o 6 = 4. L a d i v e r g e n c i a es
m u y regular. E n c a m b i o , u n incremento m a r g i n a l de 6 a 4.1 hace
que l a d i v e r g e n c i a sea m u c h o más v i o l e n t a y s i 6 s i g u i e r a a u m e n t a n d o
sería todavía m a y o r .
E n términos matemáticos, c u a n d o 6 < 4 las raíces son e x a c t a mente u n i t a r i a s y, p o r t a l razón, el m o d e l o flota alrededor d e l e q u i l i b r i o s i n convergir n i d i v e r g i r . C u a n d o 8 = 4, las raíces son reales,
repetidas y u n i t a r i a s , pero e l modelo c o m i e n z a a d i v e r g i r , a u n q u e de
f o r m a l i n e a l , p o r q u e las soluciones de ecuaciones dinámicas c o n raíces
reales y repetidas i n v o l u c r a u n a t e n d e n c i a lineal (ver C h i a n g , 1984,
p. 508 y L a k s h m i k a n t h a m y T r i g i a n t e , 1988). E n c a m b i o , s i 6 > 4,
c u a n d o menos a l g u n a de las raíces es m a y o r que l a u n i d a d y e l m o d e l o
diverge.
E l efecto i n i c i a l de u n aumento en l a t a s a de creación de d i n e r o es
s i m i l a r a l d e l m o d e l o I. E n u n p r i n c i p i o , l a t a s a de creación de dinero
afecta únicamente e l p r o d u c t o , m i e n t r a s que l a inflación permanece
constante porque está d e t e r m i n a d a sólo p o r variables retrasadas. E n
el período 2 l a inflación a u m e n t a porque e l p r o d u c t o d e l período a n terior aumentó y e l p r o d u c t o e m p i e z a a caer. E l p r o b l e m a es que
no h a y f o r m a en l a que e l m o d e l o p u e d a estacionarse de nuevo en el
e q u i l i b r i o de largo plazo.
E s t a versión d e l m o d e l o sugiere que l a c o m p e t e n c i a p u e d e tener
efectos perversos. U n incremento de 6 eleva l a c o m p e t e n c i a e n e l m e r cado de t r a b a j o y, p o r consiguiente, a u m e n t a e l p r o d u c t o d e l estado
estacionario. N o obstante, también p r o p i c i a ciclos más irregulares e
incluso divergentes, lo c u a l a t e n t a c o n t r a el bienestar de l a población.
Sólo en e l caso de que l a c o m p e t e n c i a fuera perfecta (8
oo) el
p r o d u c t o se estabilizaría en u n valor constante.
U n a p r e g u n t a i m p o r t a n t e que surge de estas conclusiones es si
u n m o d e l o que diverge puede s o b r e v i v i r . L a respuesta es n e g a t i v a en
el largo p l a z o , p e r o puede ser p o s i t i v a en el corto y a u n en e l m e d i a n o
plazo.
U n m o d e l o c o m o e l I I , el c u a l diverge cuando 6 es m a y o r que
4, no puede s o b r e v i v i r b a j o argumentos económicos plausibles, pues
198
ESTUDIOS ECONÓMICOS
los recursos son l i m i t a d o s y los precios positivos. L a s oscilaciones
cada vez mayores requerirían que en algunos períodos se p r o d u j e r a n
cantidades superiores a las que es posible p r o d u c i r . Inflaciones m u y
negativas harían que el n i v e l de precios p a s a r a de p o s i t i v o a n e g a t i v o ,
lo c u a l n o tiene sentido económico. S i n embargo, c u a n d o u n m o d e l o
que diverge está en el estado estacionario y hay u n choque infinitesi¬
m a l m e n t e pequeño en u n parámetro, las oscilaciones que m u e s t r a e n
un p r i n c i p i o son también pequeñas - a u n q u e c r e c i e n t e s - y son c o m patibles con l a c a n t i d a d d i s p o n i b l e de recursos de u n a economía y c o n
la condición de no n e g a t i v i d a d de los precios. Así que p o r u n t i e m p o
relativamente largo sería posible que u n a economía p u d i e r a s o b r e v i v i r
con u n c o m p o r t a m i e n t o explosivo de sus variables.
4. S e n s i b i l i d a d de los m o d e l o s a los parámetros y
compleja
dinámica
E l análisis d e l m o d e l o I m u e s t r a que es estable y converge a los valores
del estado estacionario c u a n d o hay u n choque en algún parámetro.
E n c a m b i o , el m o d e l o II es inestable y flota alrededor d e l estado e s t a c i o n a r i o c u a n d o algún parámetro c a m b i a o de hecho puede, i n c l u s o ,
divergir.
U n a p r e g u n t a relevante desde el p u n t o de v i s t a d e l análisis dinám i c o es sobre l a s e n s i b i l i d a d de los modelos a l a regla s a l a r i a l y a los
parámetros. E s claro que este t r a b a j o h a demostrado que e l m o d e l o
t r a d i c i o n a l de l a c u r v a de P h i l l i p s es altamente sensible a m o d i f i c a ciones aparentemente insustanciales de l a regla s a l a r i a l . L a p r e g u n t a
a h o r a sería qué t a n sensibles son los modelos presentados a l valor de
los parámetros.
L a respuesta a n t i c i p a d a es que el modelo I no es sensible a los
parámetros. S i estos son similares, el modelo converge a valores t a m bién similares. N o obstante, el modelo II sí es a l t a m e n t e sensible a l
valor de los parámetros y e l c o m p o r t a m i e n t o dinámico de las v a r i a b l e s
es m u y diferente ante cambios m u y pequeños en dichos parámetros.
De aquí que el m o d e l o I I , aunque lineal y con patrones definidos, p r e senta características que n o r m a l m e n t e se a t r i b u y e n a modelos caóticos.
4.1.
S e n s i b i l i d a d d e l o sm o d e l o s I y I I a los
parámetros
Las simulaciones se h i c i e r o n t o m a n d o en cuenta que r es 0.5 y que
estando en el estado estacionario l a t a s a de creación de d i n e r o n p a s a
del 30 p o r ciento a l 50.
A J U S T E SALARIAL
L a gráfica 6 m u e s t r a
del ingreso en e l m o d e l o I
claro que las trayectorias
entre las dos variables es,
199
u n d i a g r a m a de fase entre las t r a y e c t o r i a s
c u a n d o 8 es 2.0 y 2.1, respectivamente. E s
son t a n similares que e l d i a g r a m a de fase
prácticamente, u n a r e c t a de 45 grados.
Gráfica 6
D i a g r a m a d efase entre d o s trayectorias d e ingreso:
c u a n d o 6 = 2.0 ( e j e x ) y c u a n d o 8 = 2.1 ( e j e y ) ,
en el modelo I con 100 observaciones
•0.161
1
E n c a m b i o , l a gráfica 7 m u e s t r a u n d i a g r a m a de fase entre los
ingresos c u a n d o en e l m o d e l o I I 8 es 2.0 y 2.1, respectivamente. E n
ambos casos el s i s t e m a recibe el choque de u n aumento en n de 30 a
50 p o r ciento.
Las t r a y e c t o r i a s d e l ingreso c u a n d o 8 = 2, o 6 es 2.1 s o n m u y
d i s t i n t a s . D e hecho, c u a n d o 8 = 2 e l modelo t o m a sólo tres valores,
ya que e l ciclo es de o r d e n 3. E n c a m b i o , cuando 6 = 2.1 e l m o d e l o
presenta u n ciclo de o r d e n múltiple, probablemente infinito, aunque
los valores que t o m a e l proceso están l i m i t a d o s a cierto r a n g o en los
números reales.
L a gráfica 7 se presenta p a r a u n a simulación c o n 100 períodos.
51 se extiende l a simulación a muchas más observaciones, se e m p i e z a
a llenar t o d o el espacio y, de m a n e r a eventual, se f o r m a u n rectángulo
200
ESTUDIOS ECONÓMICOS
c o m p l e t a m e n t e denso. C u a n d o el número de observaciones tiende a
i n f i n i t o , l a correlación estadística entre las dos trayectorias d e ingreso
presentadas es, prácticamente, i g u a l a cero.
Gráfica 7
D i a g r a m a d efase entre dos trayectorias de ingreso:
c u a n d o 6 = 2.0 ( e j e x ) y c u a n d o 6 = 2.1 ( e j e y ) ,
en el modelo I I con 100 observaciones
0.0
•0.5-1
,
-0.4
,
-0.2
-0.3
r-0.1
YDB
E s posible repetir este ejercicio c o n pares de valores d i s t i n t o s ,
pero m u y similares, y el r e s u l t a d o es, prácticamente, el m i s m o . C u a n do l a simulación se registra p a r a u n número relativamente r e d u c i d o
de períodos, es c o m p l e j a l a figura que se f o r m a entre el ingreso c u a n d o
S t o m a u n cierto valor o c u a n d o t o m a otro m u y cercano.
C u a n d o l a simulación se r e a l i z a p a r a muchos períodos entonces
se f o r m a u n rectángulo bien definido. E n los casos analizados l a c o r relación estadística entre los dos ingresos (con u n a c i e r t a 6 y con u n
valor m u y cercano) t e r m i n a siendo c e r o .
18
Los ejercicios se hicieron tomando 65 000 períodos y las correlaciones se
calcularon en el programa econométrico E - v i e w s , en donde también se dibujaron
los diagramas de fase.
1 0
A J U S T E SALARIAL
201
L a gráfica 8 m u e s t r a o t r a simulación entre los ingresos c u a n d o
6 = 3.99 y c u a n d o es i g u a l a 3.98. E l d i a g r a m a de fase p a r a u n a
simulación de 255 observaciones m u e s t r a u n patrón m u y c o m p l e j o ,
algo s i m i l a r a u n a explosión. C o n 65 000 observaciones habría u n
rectángulo denso y l a correlación estadística entre ambos ingresos
sería cero.
Gráfica 8
D i a g r a m a d efase entre dos trayectorias de ingreso:
c u a n d o 6 = 3.99 ( e j e x ) y c u a n d o 6 = 3.98 ( e j e y ) ,
con 255 observaciones
YTMJNUB
4.2. O r d e n múltiple
e n l o sciclos del modelo I I
E l análisis de las diferentes simulaciones en el modelo I I m u e s t r a u n
patrón m u y p e c u l i a r en el c o m p o r t a m i e n t o dinámico de las variables.
C u a n d o S t o m a valores enteros menores que 4 (1, 2 y 3) los ciclos
que se generan son de o r d e n finito. C o n 6 valiendo 1 los ciclos son
de o r d e n 6. S i 8 es 2 entonces se generan ciclos de o r d e n 4 y si vale
3 surgen ciclos de o r d e n 3. E n cambio si 6 t o m a valores no enteros,
t o d o parece i n d i c a r que se crean ciclos de orden infinito, es decir, u n
202
ESTUDIOS ECONÓMICOS
número incontable de bifurcaciones, aunque l i m i t a d a s en el espacio
de los números reales en ciertos intervalos.
L a s gráficas de las series de ingreso de l a sección 3 y d e l apéndice
sugieren que el o r d e n de los ciclos es finito, porque l a serie parece
repetirse en el t i e m p o , pero u n análisis más d e t a l l a d o de las series
s i m u l a d a s m u e s t r a que los valores que en l a gráfica parecen iguales
no lo son en r e a l i d a d , son t a n sólo valores m u y cercanos entre sí.
E s t o último parece confirmarse a l graficar diagramas de fase entre l a
inflación y el ingreso con diversos números de observaciones.
L a s gráficas 9 y 10 m u e s t r a n diagramas de fase p a r a l a inflación
y el ingreso c u a n d o 6 = 2.1. E n ambos casos l a inflación está en el eje
v e r t i c a l y el p r o d u c t o en el eje h o r i z o n t a l . E s claro que h a y patrones
dinámicos m u y peculiares.
L a gráfica 9 m u e s t r a que, p a r a pocas observaciones (100), se v a n
creando polígonos m u y s i m i l a r e s , pero no exactamente iguales, entre
sí. E s t o i m p l i c a que, c u a n d o el sistema d a u n a v u e l t a c o m p l e t a , el
A J U S T E SALARIAL
203
lugar a l que llega n o es e x a c t a m e n t e el m i s m o d e l que salió, s i n o sólo
muy s i m i l a r .
L a gráfica 10 m u e s t r a u n a simulación p a r a 255 observaciones.
E n ese caso l a g r a n c a n t i d a d de polígonos que se generaron f o r m ó u n
patrón casi denso entre l a elipse más i n t e r n a y l a más e x t e r n a . S i los
ciclos d e l ingreso y l a inflación fueran de o r d e n finito, entonces sólo se
habría f o r m a d o u n polígono. A l h a b e r u n patrón denso, lo que sucedió
es que se generaron más polígonos adjuntos a l p r i m e r o , lo que sugiere
que los ciclos d e l ingreso y l a inflación p u d i e r a n ser de o r d e n i n f i n i t o .
A l llevar a cabo u n d i a g r a m a de bifurcación entre 6 y e l número d e
valores a los que converge e l proceso este número podría ser i n f i n i t o ,
aunque l i m i t a d o e n u n c i e r t o intervalo de los números reales.
Gráfica 10
D i a g r a m a d ef a s e e n t r e el i n g r e s o (eje x ) y
la inflación ( e j e y ) , c u a n d o 6 = 2 . 1 ,
con 255 observaciones
Simulaciones n o presentadas aquí m u e s t r a n que p a r a m u c h a s o b servaciones el patrón que se f o r m a entre l a elipse i n t e r n a y l a e x t e r n a
es c o m p l e t a m e n t e denso. E s t o sucede, p o r ejemplo, en u n a simulación
d o n d e e l número de observaciones es de 65 000. E s t e a r g u m e n t o a p o y a
la hipótesis de que c u a n d o 6 t o m a valores no enteros puede h a b e r c i clos de o r d e n infinito en e l m o d e l o I I .
204
5.
ESTUDIOS ECONÓMICOS
Conclusiones
E n el contexto d e l modelo simple presentado en este artículo, las r e glas salariales que m i r a n exclusivamente a l pasado le i m p r i m e n m á s
i n e s t a b i l i d a d a l s i s t e m a dinámico, que aquéllas que reaccionan a l d e sempleo observado en el m o m e n t o . E s t a diferencia m a r g i n a l p r o p i c i a
estados estacionarios idénticos, pero reacciones dinámicas a los d i v e r sos choques m u y d i s t i n t a s , dependiendo de l a regla en cuestión.
L o s resultados obtenidos dependen de l a e s t r u c t u r a d e l m o d e lo presentado, y no pueden generalizarse de m a n e r a d i s c r e c i o n a l a
situaciones más realistas. S i n embargo, son útiles pues sugieren que
ciertos efectos dinámicos que tienen lugar en el contexto s i m p l i f i c a d o
del artículo, también podrían o c u r r i r en l a r e a l i d a d .
U n a p r e g u n t a que surge del modelo a n a l i z a d o es si en economías
reales las pequeñas diferencias i n s t i t u c i o n a l e s que existen en países
similares, p u e d e n d a r lugar a m o v i m i e n t o s dinámicos m u y d i s t i n t o s
que a l a l a r g a p r o p i c i e n diferencias m u y grandes entre dichos países.
L a respuesta m u y probablemente sea p o s i t i v a , más c u a n d o se a t i e n d e
al hecho de que u n m o d e l o con supuestos t a n simples c o m o el aquí
presentado puede d a r lugar a u n a dinámica relativamente c o m p l e j a .
E n a p a r i e n c i a , p o r ejemplo, l a r e a l i d a d podría exacerbar todavía más
los efectos de pequeñas diferencias en algunas reglas de ajustes de
precios.
B a s a d o s en los resultados del modelo hay entonces dos c o n c l u siones fundamentales que surgen de este t r a b a j o :
L a p r i m e r a es que, pequeñas diferencias en algunas reglas de i n dexación y ajuste de precios t a l vez tengan u n g r a n i m p a c t o en l a
t r a y e c t o r i a dinámica de ciertas variables macroeconómicas ( h i p e r s e n s i b i l i d a d a las reglas). E n contextos más realistas y con i n t e r a c ciones más complejas entre muchas variables, diferentes formas de
indexación de los salarios a l pasado, es m u y probable generen e s t a dos estacionarios similares pero, ante ciertos choques, m o v i m i e n t o s
dinámicos m u y d i s t i n t o s p a r a las variables reales.
L a segunda conclusión es que, dadas ciertas reglas de ajuste de
precios es probable que, en economías reales, cambios marginales de
los parámetros m o d i f i q u e n de m a n e r a sensible l a respuesta dinámica
de las variables reales a diversos choques ( h i p e r s e n s i b i l i d a d a los
parámetros).
L o anterior d a lugar a u n a reflexión. S i en u n contexto más r e a l i s t a u n a economía tiene ciertas reglas de ajuste de precios que generan
h i p e r s e n s i b i l i d a d a los parámetros, es posible que d i c h a economía e n frente u n a g r a n i n c e r t i d u m b r e en presencia de diversos choques. E s t o
A J U S T E SALARIAL
205
sucede p o r q u e es m u y difícil saber c o n certeza cuál es e l valor e x a c t o
de u n parámetro. E n e l m o d e l o a n a l i z a d o , s i el parámetro 6 es 3.9999
o 4.00001, l a dinámica d e l p r o d u c t o e n e l largo plazo es m u y diferente.
L a econometría n o sería de g r a n a y u d a e n este caso, pues u n v a l o r
p u n t u a l de 4.0 n o puede rechazar n i e l 3.9999, n i el 4.00001. A s í q u e ,
no es posible p r o n o s t i c a r c o n certeza cuál es, realmente, e l efecto de
largo p l a z o de u n choque m o n e t a r i o o real.
E s t o último sugiere q u e , s i e n efecto, ciertas reglas p r o p i c i a n
h i p e r s e n s i b i l i d a d de las variables macroeconómicas a los parámetros
es necesario m o d i f i c a r l a s . E n e l m o d e l o de este t r a b a j o u n a r e f o r m a
l a b o r a l q u e incremente 6 h a s t a e l i n f i n i t o eliminaría l a h i p e r s e n s i b i l i dad a los parámetros. E n situaciones reales, las autoridades m o n e t a rias y fiscales deberían evaluar c ó m o las d i s t i n t a s reglas salariales y de
precios afectan l a dinámica de variables macroeconómicas clave y, e n
su caso, buscar u n a negociación c o n los distintos actores económicos
p a r a m o d i f i c a r las reglas que generan m a y o r i n e s t a b i l i d a d dinámica.
A l g u n a s experiencias históricas m u e s t r a n que las a u t o r i d a d e s
pueden c o n t r i b u i r p a r a m o d i f i c a r ciertas reglas de ajuste de precios.
Los gobiernos de Israel (en 1985) y México (en 1988) i n t e r v i n i e r o n
p a r a m o d i f i c a r diversas reglas de indexación de precios y salarios que
imprimían i n e r c i a a l proceso inflacionario. E n B r a s i l e l gobierno h a
i n t e r v e n i d o e n m u y diversas ocasiones p a r a establecer reglas de i n dexación s a l a r i a l (ver G o n z a g a y S c a n d i u z z i , 1998).
S i es i n v i a b l e m o d i f i c a r las reglas que generan i n e s t a b i l i d a d d i námica, las autoridades deberían buscar otros caminos. Sería c o n veniente revisar s i algunas políticas contracíclicas pueden a n u l a r los
efectos de ciertos choques.
Los resultados de este t r a b a j o i n v i t a n a seguir investigando los
efectos de cambios marginales de ciertas reglas de ajuste de precios
en l a t r a y e c t o r i a dinámica de modelos que p u e d a n s i m u l a r s i t u a ciones más realistas. D e encontrarse resultados similares a los de
este artículo, también podrían empezar a modelarse algunas políticas
adecuadas p a r a e s t a b i l i z a r l a economía.
Bibliografia
Akerlof, G . , W . Dickens y G . Perry (2000). "Near Rational Wage and Price
Setting and the Long Run Phillips Curve", Brookings
Papers
on Economic
Activity,
1, pp. 1-44.
(1996). "The Macroeconomics of Low Inflation", Brookings
nomic Activity,
1, pp. 1-59.
Papers
Bean, C. (1983). "Targeting Nominal Income: an Appraisal", E c o n o m i c
93, pp. 806-819.
on EcoJournal,
206
ESTUDIOS ECONÓMICOS
Benassy, J . P. (2002). "Optimal Monetary and Fiscal Policy Under Wage and
Price Rigidities", Macro-economic
D y n a m i c s , 6, pp. 429-441.
Blanchard, O. (1990). "Why Does Money Affects Output?", en B. Friedman y
F. Hahn (comps.), Handbook
of M o n e t a r y E c o n o m i c s , vol 2, North Holland,
Amsterdam.
y S. Fischer (1989). Lectures
o n M a c r o e c o n o m i c s , The M I T Press, Cambridge, Mass.
Blanchard, O. y D . Pérez Enrri (2000). Macroeconomía: teoría y política económ i c a con aplicaciones
a América Latina,
Prentice Hall.
Blanchflower, D. y A . Oswald (1994). The Wage
Curve,
The M I T Press, Cambridge, Mass.
Brainard, W . y G . Perry (2000). "Making Policy in a Changing World", en W .
Brainard y G . Perry (comps.), E c o n o m i c E v e n t s , Ideas and P o l i c i e s : T h e
1 9 6 0 ' s and A f t e r , Brookings Institution.
Calvo, G . y C. Vegh (1994). "Stabilization Dynamics and Backward Looking
Contracts", Journal
o f D e v e l o p m e n t E c o n o m i c s , 43, pp. 59-84.
Chiang, A . (1984). Fundamental
Methods
of Mathematical
E c o n o m i c s , 3a. ed.,
International Student Edition, McGraw Hill.
Crowley, J . (1997). The Effects
of Forward
versus
Backward
Looking
Wage
Indexation
o n Price
Stabilization
Programmes,
IMF Working Paper Series,
WP/97/38, IMF.
Desai, M . (1973). "Growth Cycles and Inflation in a Model of Class Struggle",
Journal
of E c o n o m i c Theory,
6, pp. 527-545.
Fair, R. C. (2000). "Testing the N A I R U Model for the United States", T h e
R e v i e w of E c o n o m i c s and Statistics,
82, pp. 64-71.
Fischer, S. (1977). "Long Term Contracts, Rational Expectations and the O p timal Money Supply Rule", reimpreso en R. Lucas y T . Sargent (comps.)
Rational
Expectations
and E c o n o m e t r i c Practice,
vol. 1, 1981, University of
Minessota Press, pp. 261-275.
Friedman, M . (1968). "The Role of Monetary Policy", A m e r i c a n E c o n o m i c R e v i e w , 58, pp. 1-17.
Gali, J . (2000). " T h e Return of the Phillips Curve and Other Recent Developments in Business Cycle Theory", Spanish
E c o n o m i c R e v i e w , 2, pp. 1-10.
y D. López Salido (2001). "Una nueva curva de Phillips para España",
M o n e d a y Crédito, pp. 265-304.
Ghezzi, P. (2001). "Backward-Looking Indexation, Credibility and Inflation Persistence", Journal
of International
E c o n o m i c s , 53, pp. 127-147.
Gonzaga, G . y J . Scandiuzzi (1998). "How Does Government Wage Policy Affect
Wage Bargaining in Brazil?", Revista
de E c o n o m e t r i a , 18, pp. 1-30.
Gordon, R. (1972). "Wage Price Controls and the Shifting Phillips Curve",
Brookings
Papers
o n E c o n o m i c A c t i v i t y , 2, pp. 385-421.
Gray, J . (1976). "Wage Indexation: A Macroeconomic Approach", Journal
of
M o n e t a r y E c o n o m i c s , 2, pp. 221-235.
Jadresic, E . (2001). "Wage Indexation and Output Stability Revisited",
Journal
of M o n e y , Credit
and Banking,
34, pp. 178-196.
(1997). What K i n d of Contracts
Underlie
Aggregate
Wage D y n a m i c s ? I M F
Working Paper Series, WP/97/67, IMF.
A J U S T E SALARIAL
207
King, R. (2000). "The New I S - L M Model: Language, Logic and Limits", E c o n o m i c Quarterly,
vol. 86, num. 3, pp. 45-103.
Lakshmikantham, V . y D . Trigiante (1988). "Theory of Difference Equations:
Numerical Methods and Applications", Mathematics
in S c i e n c e and E n ginering,
vol. 181.
Modigliani, F . y T . Padoa-Shioppa (1978). The Economy
with 1 0 0 % plus
Wage
I n d e x a t i o n , M I T , (mimeo).
Phelps, E . (1970). "Money Wage Dynamics and Labour Market Equilibrium",
en E . S. Phelps (comp.), M i c r o e c o n o m i c Foundations
of E m p l o y m e n t and
Inflation
Theory,
Norton, Nueva York.
(1967). "Phillips Curves, Expectations of Inflation and Optimal Unemployment Over T i m e " , E c o n o m i c a , 34, pp. 254-281.
Poole, W . (1970). "Optimal Choice of Monetary Policy Instruments in a Simple
Sthocastic Macro Model", Quarterly
Journal o f E c o n o m i c s , 84, pp. 197-216.
Roberts, J . (1997). The Wage C u r v e and the Phillips
Curve, Finance and Economics Discussion Paper Series, 1997/57, Board of Governors of the Federal
Reserve System.
Romer, D . (1996). Advanced
M a c r o e c o n o m i c s , McGraw Hill.
Rowthorn, R. E . (1977). "Conflict, Inflation and Money", Cambridge
Journal o f
E c o n o m i c s , 1, pp. 215-239.
Taylor, J . (1980). "Aggregate Dynamics and Staggered Contracts", Journal o f
Political
Economy,
88, pp. 1-23.
(1979). "Staggered Wage Setting in a Macro Model", A m e r i c a n E c o n o m i c
R e v i e w , 69, pp. 108-113.
Taylor, L . (1991). I n c o m e Distribution,
Inflation
and Growth,
The M I T Press,
Cambridge, Mass.
Tobin, J . (1972). " T h e Wage Price Mechanism: Overview of the Conference",
en O . Ekstein (comp.), The E c o n o m e t r i c s of Price D e t e r m i n a t i o n , Board of
Governors of the Federal Reserve Bank.
Trump, M . (1998). What is Chaos?,
Ilya Prigogine Center for Studies in Statistical Mechanics and Complex Systems, Universidad de Texas en Austin,
http://order.ph.utexas.edu/chaos/
Apéndice
P a t r o n e s dinámicos d e l modelo
Con
II
o b j e t o de c o m p l e m e n t a r l a explicación
sobre l a dinámica
m o d e l o I I , el apéndice m u e s t r a más s i m u l a c i o n e s d e l m o d e l o
del
bajo
diversos s u p u e s t o s , los cuales se r e s u m e n en el c u a d r o A . l .
L o s supuestos p a r a las s i m u l a c i o n e s son m u y s i m i l a r e s , s i m p l e m e n t e se p r e s e n t a n c u a t r o ejemplos:
u n o donde 6 = 2.5, q u e y a se
mostró e n e l t e x t o , o t r o en el que 6 = 3.99, u n o más donde 6 t o m a e l
v a l o r de 3.9999, y u n último c o n 6 = 4.0001.
208
ESTUDIOS ECONÓMICOS
Se presentan las gráficas de l a dinámica d e l p r o d u c t o a lo l a r g o
del t i e m p o , u n a vez que l a t a s a de creación de dinero n p a s a de 0.3 a
0.5.
E l ejemplo donde 6 =2.5 se llevó a cabo p a r a m o s t r a r que, a l
t o m a r más períodos, se c o m i e n z a n a observar ciertos patrones en l a
gráfica. E s t e m i s m o fenómeno se repite p a r a otros valores de 6. L o
que p e r m i t e descartar l a presencia de caos en el sentido más e s t r i c t o ,
pues las simulaciones m u e s t r a n c i e r t a p e r i o d i c i d a d , lo c u a l n o o c u r r e
en sistemas caóticos (ver T r u m p , 1998).
P o r o t r a p a r t e , los ejemplos donde 6 = 3.99, a 3.9999 o a 4.0001,
son elocuentes p o r sí m i s m o s . C u a n d o 6 = 3.99, el p r o d u c t o despliega
grupos de ciclos que, c o m o b u r b u j a s , v a n convergiendo y d i v e r g i e n d o
del estado estacionario. C u a n d o 6 = 3.9999, los ciclos son s i m i l a r e s ,
pero m u y largos y e l patrón i n i c i a l de los ciclos parece m u y armónico,
pero finalmente es cóncavo. E n c a m b i o , cuando 6 = 4.0001, el c i c l o
deja de ser cóncavo y se convierte en convexo, p a r a e x p l o t a r y n o
regresar n u n c a a l estado estacionario. E s interesante c o m p a r a r este
patrón con el ciclo cuando 6 = 4, en donde el patrón d e l c i c l o no es
ni cóncavo n i convexo, sino recto.
E s t e análisis m u e s t r a que dos economías que tienen parámetros
muy similares, p o r ejemplo, u n a con 6 = 3.999 y o t r a con 6 = 4.0001,
tienen u n c o m p o r t a m i e n t o , probablemente, m u y s i m i l a r a l i n i c i o de
un choque. N o obstante, conforme pasa el t i e m p o estas economías
se c o m p o r t a n en f o r m a m u y diferente, por lo c u a l es posible c o n c l u i r
que l a dinámica de largo plazo es hipersensible a los parámetros.
Cuadro A 1
Supuestos para simulaciones
2
1
3
4
6
2.5
3.99
3.999
4.0001
T
0.5
0.5
0.5
0.5
MO
0.3
0.3
0.3
0.3
V
0.0
0.0
0.0
0.0
M
0.5
0.5
0.5
0.5
""o
0.3
0.3
0.3
0.3
Yo
-0.2
-0.125
-0.125
-0.124
210
ESTUDIOS ECONÓMICOS
Gráfica
6 =
A.3
3.9999
— Serie 1