06. LA PROPORCIÓN
Anuncio
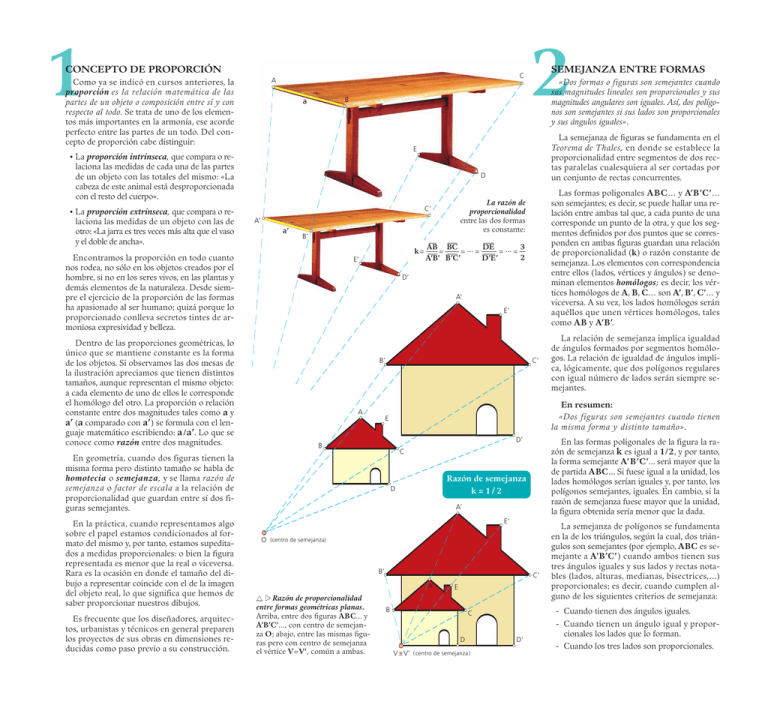
1 CONCEPTO DE PROPORCIÓN • • C A Como ya se indicó en cursos anteriores, la proporción es la relación matemática de las partes de un objeto o composición entre sí y con respecto al todo. Se trata de uno de los elementos más importantes en la armonía, ese acorde perfecto entre las partes de un todo. Del concepto de proporción cabe distinguir: B a C’ a’ B’ k= E’ Es frecuente que los diseñadores, arquitectos, urbanistas y técnicos en general preparen los proyectos de sus obras en dimensiones reducidas como paso previo a su construcción. Las formas poligonales A BC… y A’B’C’… son semejantes; es decir, se puede hallar una relación entre ambas tal que, a cada punto de una corresponde un punto de la otra, y que los segmentos definidos por dos puntos que se corresponden en ambas figuras guardan una relación de proporcionalidad (k) o razón constante de semejanza. Los elementos con correspondencia entre ellos ( lados, vértices y ángulos ) se denominan elementos homólogos; es decir, los vértices homólogos de A, B, C… son A’, B’, C’… y viceversa. A su vez, los lados homólogos serán aquéllos que unen vértices homólogos, tales como AB y A’B’. La razón de proporcionalidad entre las dos formas es constante: A’ AB BC ... DE ... 3 = = = = = 2 A’B’ B’C’ D’E’ D’ A’ E’ B’ A C’ D’ B En las formas poligonales de la figura la razón de semejanza k es igual a 1/ 2, y por tanto, la forma semejante A’ B’C’... será mayor que la de partida ABC... Si fuese igual a la unidad, los lados homólogos serían iguales y, por tanto, los polígonos semejantes, iguales. En cambio, si la razón de semejanza fuese mayor que la unidad, la figura obtenida sería menor que la dada. C Razón de semejanza k = 1/2 D A’ E’ O (centro de semejanza) B’ C’ A Razón de proporcionalidad entre formas geométricas planas. Arriba, entre dos figuras ABC... y A’B’C’..., con centro de semejanza O; abajo, entre las mismas figuras pero con centro de semejanza el vértice V=V’, común a ambas. La relación de semejanza implica igualdad de ángulos formados por segmentos homólogos. La relación de igualdad de ángulos implica, lógicamente, que dos polígonos regulares con igual número de lados serán siempre semejantes. En resumen: «Dos figuras son semejantes cuando tienen la misma forma y distinto tamaño». E En geometría, cuando dos figuras tienen la misma forma pero distinto tamaño se habla de homotecia o semejanza, y se llama razón de semejanza o factor de escala a la relación de proporcionalidad que guardan entre sí dos figuras semejantes. En la práctica, cuando representamos algo sobre el papel estamos condicionados al formato del mismo y, por tanto, estamos supeditados a medidas proporcionales: o bien la figura representada es menor que la real o viceversa. Rara es la ocasión en donde el tamaño del dibujo a representar coincide con el de la imagen del objeto real, lo que significa que hemos de saber proporcionar nuestros dibujos. La semejanza de figuras se fundamenta en el Teorema de Thales, en donde se establece la proporcionalidad entre segmentos de dos rectas paralelas cualesquiera al ser cortadas por un conjunto de rectas concurrentes. D Encontramos la proporción en todo cuanto nos rodea, no sólo en los objetos creados por el hombre, si no en los seres vivos, en las plantas y demás elementos de la naturaleza. Desde siempre el ejercicio de la proporción de las formas ha apasionado al ser humano; quizá porque lo proporcionado conlleva secretos tintes de armoniosa expresividad y belleza. Dentro de las proporciones geométricas, lo único que se mantiene constante es la forma de los objetos. Si observamos las dos mesas de la ilustración apreciamos que tienen distintos tamaños, aunque representan el mismo objeto: a cada elemento de uno de ellos le corresponde el homólogo del otro. La proporción o relación constante entre dos magnitudes tales como a y a’ ( a comparado con a’ ) se formula con el lenguaje matemático escribiendo: a / a’. Lo que se conoce como razón entre dos magnitudes. «Dos formas o figuras son semejantes cuando sus magnitudes lineales son proporcionales y sus magnitudes angulares son iguales. Así, dos polígonos son semejantes si sus lados son proporcionales y sus ángulos iguales». E La proporción intrínseca, que compara o relaciona las medidas de cada una de las partes de un objeto con las totales del mismo: «La cabeza de este animal está desproporcionada con el resto del cuerpo». La proporción extrínseca, que compara o relaciona las medidas de un objeto con las de otro: «La jarra es tres veces más alta que el vaso y el doble de ancha». 2 SEMEJANZA ENTRE FORMAS E B - Cuando tienen dos ángulos iguales. C D V V’ ( centro de semejanza ) La semejanza de polígonos se fundamenta en la de los triángulos, según la cual, dos triángulos son semejantes (por ejemplo, ABC es semejante a A’B’C’ ) cuando ambos tienen sus tres ángulos iguales y sus lados y rectas notables (lados, alturas, medianas, bisectrices,…) proporcionales; es decir, cuando cumplen alguno de los siguientes criterios de semejanza: D’ - Cuando tienen un ángulo igual y proporcionales los lados que lo forman. - Cuando los tres lados son proporcionales.