apuntes magnetismo - UTN - Universidad Tecnológica Nacional

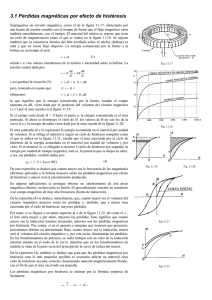
UNIVERSIDAD TECNOLÓGICA NACIONAL
FACULTAD REGIONAL MENDOZA
DEPARTAMENTO DE ELECTRÓNICA
CÁTEDRA DE TECNOLOGÍA ELECTRÓNICA
MATERIALES MAGNÉTICOS
PROFESOR TITULAR:
ING. ADOLFO F. GONZÁLEZ
PROFESOR ADJUNTO:
ING. RICARDO M. CESARI
AYUDANTE TRABAJOS PRÁCTICOS:
ING. RUBÉN O. VICIOLI
2009
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
ÍNDICE
REPASO DE UNIDADES ________________________________________________________________ 3
Flujo Magnético Φ ____________________________________________________________________ 3
Inducción magnética B ________________________________________________________________ 3
Intensidad de campo magnético H _______________________________________________________ 3
Tensión magnética V o f.m.m. ___________________________________________________________ 4
Magnetización o Inducción específica δ ___________________________________________________ 4
Permeabilidad μ ______________________________________________________________________ 4
INTRODUCCIÓN ______________________________________________________________________ 5
Temperatura Curie____________________________________________________________________ 6
Ley de Ohm en el campo magnético ______________________________________________________ 7
Ciclo de Histéresis Normal y Curvas de Magnetización _______________________________________ 8
Permeabilidad _______________________________________________________________________ 9
Permeabilidad Incremental μΔ__________________________________________________________ 11
Cambios de energía producidos durante el ciclo magnético ___________________________________ 13
Pérdidas en los materiales magnéticos ___________________________________________________ 14
Pérdidas por Histéresis Ph___________________________________________________________ 14
Pérdidas por corrientes parásitas o de Foucault __________________________________________ 15
Efecto pelicular magnético ___________________________________________________________ 17
Descripción y clasificación de materiales magnéticos ________________________________________ 18
Forma de la curva o lazo de histéresis ___________________________________________________ 18
Ejemplo de materiales con distintos lazos de histéresis ____________________________________ 18
Producto de Energía Especifica (PEE) ___________________________________________________ 21
Ferritas para Imanes Permanentes ______________________________________________________ 22
Cintas Magnéticas ___________________________________________________________________ 23
Cerámicas Magnéticas _______________________________________________________________ 23
Materiales y Aleaciones para laminaciones ________________________________________________ 24
Fe - Si de Grano Orientado ____________________________________________________________ 25
Núcleos para Inductores y Transformadores con cinta arrollada. _______________________________ 26
Cazoletas __________________________________________________________________________ 26
Laminación E-I ______________________________________________________________________ 26
BIBLIOGRAFÍA _______________________________________________________________________ 28
-2–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
REPASO DE UNIDADES
Flujo Magnético Φ
Es la cantidad total de líneas de fuerza, generadas en el medio magnético. Desde el punto
de vista práctico nos interesa que Φ sea grande con un mínimo de energía eléctrica.
Φ = ∫ B.ds
Donde:
B: inducción magnética.
s: sección del núcleo.
Cgs: 1 Mx (Maxwell)
MKS: 1 Wb (weber) = 1 V.s
Inducción magnética B
Es la medida de la concentración del flujo. B es igual a la cantidad de líneas de fuerza que
2
atraviesan la unidad de superficie perpendicular a Φ en 1 cm .
B = μ.H en un medio magnético.
Cgs: 1 Gs (gauss) = Mx/cm2
MKS: 1 Wb/m2 = l V.s/m2
1 T (Tesla) = 1 Wb/m2 = 10 KGs.
El Tesla es la unidad de flujo adoptado por el SI (Sistema Internacional).
B0 = H en el vacío.
Intensidad de campo magnético H
(También denominado fuerza magnetizante) es la medida del efecto de la corriente eléctrica
que c ircula p or el dev anado y es i gual a l a f racción de f .m.m., c orrespondiente a l a uni dad d e
longitud del circuito magnético excitado por el devanado.
Cgs:
H=
0,4 ⋅ Π ⋅ N ⋅ I
= O e [Oesterd]
l
MKS:
H=
N⋅I
= A/m (a veces se expresa A .vueltas/m)
l
-3–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
N:
n3 espiras.
I:
corriente eléctrica.
l:
longitud del circuito magnético.
1 Oe = 80 A / m
Tensión magnética V o f.m.m.
Es la intensidad de campo total aplicada al circuito magnético.
f.m.m = ∫ H.dl
cgs:
1 Gb (Gilbert) = 1 Oe.cm
MKS:
1 A (amperio) = 1 Joule/Wb a veces se expresa = A.vueltas
Nota: debido a que μr = 1 ( por def inición, en el s istema CGS) e s c orrecto u sar O esterd y
Gauss indistintamente.
Magnetización o Inducción específica δ
B en un punto del campo magnético se compone de dos valores: uno el que se obtendría en
el vacío (μ0H), el otro representa la influencia ejercida por el medio.
Este segundo valor se llama "magnetización" o "inducción específica".
Cgs:
4 ⋅ Π ⋅ ∂ = B - μ0 ⋅ H
MKS:
∂ = B − μ0 ⋅ H
En el sistema cgs la magnitud es 4Π veces menor al racionalizado.
Permeabilidad μ
Retomando la expresión B = μ.H, μ se llama permeabilidad y se puede expresar:
μ = μ0 ⋅μr
μ0 = permeabilidad del vacío.
Μr = permeabilidad relativa con respecto a la del vacío, para el vacío μr = 1.
cgs = 1 (por definición).
MKS = 4.Π.10-7 H / m.
Μr es a dimensional como Xm
-4–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
INTRODUCCIÓN
Las propiedades magnéticas, tienen su origen en la existencia de dipolos magnéticos en los átomos,
por resultado del movimiento de los electrones.
Un c ampo m agnético ex terno t iende a al inear es tos di polos, s egún su m isma di rección, c on l a
consiguiente aparición de momentos magnéticos inducidos en el material.
El momento magnético total por unidad de volumen, se denomina Magnetización M del material y es
equivalente a la polarización P de los dieléctricos.
Desde el a specto t ecnológico, l os m ateriales m agnéticos h an s ido de sarrollados de sde 193 0
aproximadamente.
Hemos vistos que en el vacío B = μ0 .H, en un sólido se puede plantear la siguiente relación:
B = μ 0 ⋅ (H + M ) = μ 0 ⋅ H + μ 0 ⋅ M
El segundo término μ 0.M es debido a la aparición de momentos dipolares en un sólido, cuando está
sumergido en un campo magnético y es un campo adicional de inducción magnética que se suma a la del
vacío absoluto.
Para nu merosas s ustancias en q ue M es p roporcional a H , se pu ede d efinir l a s usceptibilidad
magnética del medio Xm.
M = Xm ⋅ H
Xm es un número puro porque H y M tienen las m ismas unidades. Teniendo en c uenta l o ant erior
puede escribirse:
B = μ 0 ⋅ (1 + X m ) ⋅ H
µ = μ 0 ⋅ (1 + X m )
Todas las s ustancias s on conductoras de flujo m agnético, pero de ac uerdo al
susceptibilidad magnética las sustancias pueden clasificarse en:
valor de s u
Diamagnéticas: Cuando Xm es (-) y pequeño comparado con 1 (μ < μ0).
A magnéticas: no magnéticas Xm = 0 (μ = μo) ambas igual a 1.
Paramagnéticas: Cuando Xm es (+) y levemente mayor a 1 (μ > μo).
Ferro magnéticas Cuando Xm es (+) y mucho mayor a 1 (μ >>> μo).
En las sustancias ferro magnéticas M no es exactamente proporcional a H, de modo que Xm no es
constante, salvo para pequeños intervalos de H. En los diamagnéticos los dipolos se orientan en la dirección
de1 campo pero en sentido opuesto, dando una inducción en el sólido menor que fuera de él.
-5–
TECNOLOGÍA ELECTRÓNICA
Bismuto
Plata
Plomo
Cobre
Agua
F.R.M. - U.T.N.
Diamagnéticos
Paramagnéticas
Aire Aluminio
Plata
Tabla 1
Tabla 2
Permeabilidad relativa (μr)
0,99983
0,99998
0,999983
0,999991
0,999991
Permeabilidad relativa (μr)
1,0000004
1,00002
A magnética o no magnética
Vacío por definición μr = μo = 1
Ferromagnéticas
Polvo de Permalloy (2-81), 2 Mo-8l
Ni d e c omposición p orcentual y el
resto Fe e impurezas
Cobalto
Níquel
Ferroxcube 3 (.Perrito Mn-Zn)
Acero dulce (0,2 C)
Hierro con Impurezas (O,2 C)
Hierro
silicio
utilizados e n
transformadores (4 Si)
Permalloy 78 (78,5 Ni)
Hierro purificado
Superpermalloy (5 Mo-79 Ni)
Tabla 3
Permeabilidad relativa (μr)
130
250
600
1.500
2.000
5000
7.000 o menor
100.000
200.000
1.000.000
La l ista es mucho más extensa y dí a a dí a surgen nuev as composiciones p rocurando m ejorar la
permeabilidad, ya sea incrementado su valor como logrando mayor tramo de linealidad.
Pero, l o i mportante que hay que t ener e n c uenta es l o s iguiente: E n un material conductor l a
resistividad es del orden 10-4; 10-6.
En un material aislante la resistividad es del orden de 1015; 1020, entre ambos el salto es de 1019 a
10 , ahora eso traslado a materiales magnéticos.
26
Un material no magnético μ = 1.
Un material ferro magnético μ está en el orden de 1 06 en el mejor de l os casos, por cuanto en l os
usos corrientes es de 103. Ahora el salto es de 103 a 106, de allí provienen las consideraciones prácticas que
hay que contemplar para evitar la dispersión de las líneas de flujo. Para Tecnología es correcto utilizar μ= 1,
para diamagnéticos, paramagnéticos, o sea igual a la del vacío.
Temperatura Curie
Se l lama así, a l a t emperatura por en cima de l a c ual, l os m ateriales ferro m agnéticos se
vuelven pa ramagnéticos. E sta c aracterística e s reversible, po rque l os m ateriales, recuperan s us
propiedades magnéticas, cuando la temperatura desciende por debajo del punto Curie. Para el Fe
es 800°C.
-6–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Ley de Ohm en el campo magnético
Supongamos un toroide donde R >> r
Figura 1
l = 2.Π.R por ser R >> r.
l = longitud del circuito magnético.
N = nº total de espiras.
S =Π.r2
S = sección del conductor.
B = μ ⋅ H ⇒ H = B/μ
Φ = B⋅s
H=
0,4 ⋅ Π ⋅ N ⋅ I
l
reemplazando:
H=
0,4 ⋅ Π ⋅ N ⋅ I B
Φ
0,4 ⋅ Π ⋅ N ⋅ I ⋅ s ⋅ μ
= =
⇒Φ=
2⋅Π⋅R
μ s⋅μ
l
reordenando:
Φ=
0,4 ⋅ Π ⋅ N ⋅ I f.m.m.
=
1 l
ℜ
⋅
μ s
Esto i ndica l a i mportancia que m s ea l o m es gr ande po sible, p orque de esa m anera se
reduce la reluctancia (R).
ℜ=
1 1
⋅
μ s
Las características que nos interesan de los materiales ferro magnéticos, son múltiples y se
pueden separar en dos grandes grupos:
-7–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
1° Aquellos que instalados en un circuito eléctrico, al paso de una corriente I, establece un
Φ que nos interesa sea lo mayor posible. La I genera un H y este un B, que da lugar al
establecimiento de un Φ. Para que B sea lo más grande posible μ tiene que ser grande.
2° Aquellos que tienen un flujo Φ para I = 0, que son los imanes permanentes.
Ciclo de Histéresis Normal y Curvas de Magnetización
La c aracterística m agnética de u n m aterial, dep ende de su historia m agnética p revia,
propiedad llamada "histéresis", que significa "atraso de fase" entre B y H.
Consideremos un t rozo de hi erro d ulce, qu e ha sido pr eviamente des magnetizado, de
formato t oroidal. ( Un m aterial magnético se de smagnetiza, s ometiéndolo a u n c ampo al terno, de
amplitud máxima continuamente decreciente hasta cero. Este proceso efectivamente destruye toda
historia magnética previa). Cuando la f.m.m. en el toro es gradualmente aumentada, la densidad de
flujo aumentará, según la curva 0-1 de la Fig. I, llegando al valor Bm cuando la intensidad de campo
aplicado es Hm. Esta curva se llama "Curva ascendente de magnetización" .Si luego alcanzado el
punto 1, l a i ntensidad d e campo e s g radualmente disminuida, l a den sidad d e f lujo c aerá según l a
curva 1-2, alcanzando el valor Br en H=0.
Esta den sidad de f lujo B r, r etenida po r el m aterial, l uego de ha ber s ido m agnetizado e s
llamada "Inducción Residual" o "Retentividad".
El ciclo es continuado aumentando H en sentido opuesto, provocando una disminución del
flujo, según la curva,2-3.
El valor magnético de Hc, necesario para llevar B a cero, es llamado "Fuerza Coercitiva"'. El
ciclo se c ompleta con l a disminución de H hasta -Hm y l uego variándolo hasta + Hm, pr oduciendo
una variación de la densidad de flujo según la curva 3-4, el punto 7 generalmente no coincidirá con
el 1, siendo un poco inferior.
Si el campo magnético es variado cíclicamente de +Hm a -Hm y viceversa ambos puntos,
gradualmente llegarán a c oincidir, formando lo que s e denomina, un " Lazo de H istéresis normal o
simétrico".
El l ugar g eométrico, de l as extremidades de l azos de histéresis d e di stinta am plitud, s e
llama "Curva Normal de Magnetización".
Ciclo normal de histéresis
Figura 2
-8–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Curva normal de magnetización
Figura 3
Gráfica de B y δ
Figura 4
La curva normal y la de primera magnetización pueden coincidir.
Permeabilidad
Figura 5
El c ociente entre B y H en cualquier pu nto d e l a c urva se conoce con el nom bre d e
"permeabilidad normal" o "estática" y ella es:
μ=
Bm
Hm
-9–
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Es l a pendi ente de l a r ecta de sde el or igen ha sta i nterceptar el punt o de l a c urva,
correspondiente a Bm.
Una recta similar trazada tangente sobre la curva, nos determina la permeabilidad máxima.
μ=
B'
H'
La pendi ente B o / H o de l a c urva n ormal, en el or igen es l o qu e s e l lama " Permeabilidad
Inicial", generalmente más pequeña que mm. Si todos los valores de permeabilidad se dividen por la
del vacío se obtienen las permeabilidades relativas.
μi =
B0
H0
El problema en si es más complejo, pues lo que se describe cíclicamente no es una curva,
sino un lazo, (área).
Supongamos que H varía sinusoidalmente entre sus valores máximos ± Hm, por lo que sus
valores instantáneos serán H = Hm .cos wt. Por lo tanto B variará entre los correspondientes límites
± Bm.
Si la curva de magnetización del hierro lo representados por una línea prácticamente recta
que un e l os punt os 1 -0-4, en l ugar del l azo de histéresis, el pr oblema c omo hem os dicho, s e
simplifica notablemente, y el valor de E en cualquier instante estará dado por una función senoidal
en fase con la de H de esta manera tendremos:
H H m ⋅ Cosωo H m
=
=
B B m ⋅ Cosωo B m
Sin embargo, debido a la existencia del lazo de histéresis, el valor actual de B coincidirá con
aquel de la función senoidal ideal solamente en dos puntos: los extremos del lazo, 4-l. La forma de
onda de B será distorsionada y tendrá aproximadamente la forma de la Figura siguiente:
Figura 6
La curva de B siempre estará por debajo de la curva ideal, mientras H aumenta, y sobre ella
mientras H d isminuye. P or l o t anto, l a c urva a ctual de B puede s uponerse compuesta p or do s
componentes, una s erá l a f unción senoidal no distorsionada y l a ot ra una f orma d e ond a
"diferencia", cuyas ordenadas serán iguales a la diferencia entre el valor correspondiente de B para
el material real y el correspondiente a un material imaginario ideal con una curva de magnetización
lineal. S e o bserva qu e la c urva di ferencia es simétrica respecto al ej e de ab scisas y por
- 10 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
consiguiente, puede s er desarrollada a una f undamental y una s erie de a rmónicas i mpares. La
forma de onda de B puede ser analizada como:
1.- una componente senoidal, en fase con el campo aplicado H.
2.- una componente senoidal, desfasada 90° respecto de H.
3.- una serie de componentes armónicas impares.
La componente en f ase de B inducirá una f.e.m. en el bobinado que estará desfasada 90°
respecto de la corriente, y por lo tanto representa la parte inductiva del inductor.
La componente de B en cuadratura induce una f.e.m. en fase con la corriente,
correspondiendo ésta a una resistencia en serie con la inductancia, e implica aquella energía que es
disipada en el núcleo como resultado del fenómeno de histéresis.
Permeabilidad Incremental μΔ
Esta magnitud es de suma importancia en el diseño de choques y transformadores por los
que circula c.c. y c.a. superpuestas. μΔ es el cociente entre ΔB y ΔH. No hay ón
restricci
c on
respecto a l as magnitudes de D B y DH así como a l a posición en el ciclo de hi stéresis o c urva de
magnetización normal considerada.
Figura 7
μΔ =
ΔB
ΔH
Cuando H tiende a cero se tiene la “Permeabilidad diferencial”
μ d = lím ΔH→0
ΔB dB
=
ΔH dH
Ho = intensidad de campo constante o sea Hcc (a la c.c.).
Si se analizan las pendientes de ΔB/ΔH y la correspondiente al unir al origen con el punto
1, (o sea la permeabilidad provocada por el campo continuo), se deduce que para cualquier valor de
Ho y ΔH será siempre mayor que μΔ.
μcc siempre > μΔ
- 11 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
En general para un valor dado de Ho debajo de la zona de saturación de la curva normal de
magnetización, l a per meabilidad p rimero aum enta y l uego di sminuye c uando H a s e i ncrementa.
También sucede que si Ha se mantiene constante y se va aumentando Hcc, los pequeños ciclos de
histéresis van disminuyendo su pendiente.
La curva " normal de m agnetización" es muy út il, por que s e l a puede reproducir m uy
fácilmente y por que es l a c aracterística de c ada tipo de m aterial m agnético, nor malmente l os
fabricantes dan un área y en cada proyecto habrá que utilizar el valor más desfavorable.
Figura 8
Volviendo a Ha, c uando es te se mantiene constante en un v alor determinado, que no s ea
muy pe queño l a permeabilidad di sminuirá a m edida q ue l a d ensidad de f lujo B d e p olarización
aumente. E sto es debi do a que l os l azos de hi stéresis s e ha cen c ada v ez m ás ho rizontales a
medida que aumenta Ho (Hcc).
Figura 9
Otra conclusión es que, Ha será variable independiente en circuitos de corriente constante y
ciertos circuitos resonantes. En los circuitos de tensión constante, Ba será la variable independiente.
Las curvas que indican la variación de μΔ en función de los distintos valores de polarización
Ho es el siguiente:
- 12 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Figura 10
curva para el Fe - Si (3,6%) y de 0,35mm de espesor.
Cambios de energía producidos durante el ciclo magnético
Figura 11
La f igura m uestra u n lazo de hi stéresis nor mal. C onsideraremos l os c ambios de ener gía
provocados a l pr oducirse el l azo. C omenzando en el punt o 6 y y endo ha cia arriba ha sta el 2, s e
observa un aumento en la inducción y por lo tanto se inducirá una tensión contra 1a circulación de
comente en 1a bobina Ge excitación.
Esto produce una absorción de energía del circuito eléctrico, cuyo valor es:
Br
W6−7 = ∫ H ⋅ dB Joule /cm3
− Br
y será evidentemente igual al área 6-1-2-7-6 de la figura. Durante la siguiente operación en el ciclo
2-3, la energía es devuelta por el hierro al circuito eléctrico, como una tensión inducida debido a la
disminución del flujo F concatenado y que posee la misma dirección que la corriente de excitación,
que se encuentra disminuyendo. Esta energía está dada por la integral:
Br
W2−3 = ∫ H ⋅ dB Joule /cm3
− Br
y que es igual al área 3-2-7-3. Los últimos pasos del ciclo, 3 a 5 y 6 a 6, son idénticos con respecto
a l os primeros d os pasos de bido a l a s imetría d el l azo r especto al o rigen. P or c onsiguiente l a
energía neta tomada del circuito eléctrico durante el ciclo magnético completo será igual a 2W6-2 2W2-3, que evidentemente es el área total abrazada por el lazo de histéresis.
- 13 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Esta en ergía s e m anifiesta c omo calor en el hi erro, y debi do a que ella e s sustraída d el
circuito eléctrico por el fenómeno de histéresis magnética, estas pérdidas se denominan "Pérdidas
por Histéresis”. El lazo de histéresis normal es importante en aparatos donde el flu­jo varía según un
ciclo de i guales v alores p ositivos y ne gativos, c omo, oc urre en l a m ayoría de l os apa ratos d e
corriente alterna.
Entonces cuando las variaciones de flujo son periódicas, puede hablarse de la potencia de
pérdida p or histéresis p or c m3 i gual al pr oducto del ár ea contenida en el l azo m ultiplicada por la
frecuencia de ex citación e n c iclos por segundo. P ara ap aratos que o peran con f lujos al ternos, se
requieren m ateriales m agnéticos qu e pos ean p érdidas p or hi stéresis pe queñas, c on el o bjeto de
aumentar la eficiencia y reducir sus dimensiones, uno de ellos puede ser Fe-Si.
Pérdidas en los materiales magnéticos
Se separan en tres:
- Pérdidas por histéresis.
- Pérdidas por corrientes parásitas (Foucault).
- Pérdidas Residuales.
Estas últimas, no se pueden explicar y pueden pasar a ser importante para bajos valores de
inducción cuando las pérdidas por histéresis y Foucault son pequeñas. Se las determina en forma
experimental, o s ea cuando s e m ide l a t otal y l uego en f orma i ndependiente l a de hi stéresis y
Foucault se acusa como diferencia, por supuesto cometiendo el mismo error durante las
mediciones.
Pérdidas por Histéresis Ph
Cuando el formato del ciclo es fácil de integrar analíticamente se procede como se
mencionó anteriormente. Pero debido a que existe una gran diversidad de formatos de lazos
a veces se hace muy complicado el método analítico y para ello se determina por medición
de la potencia perdida en la masa magnética o bien haciendo una integración gráfica.
La en ergía gastada e stará pe rfectamente det erminada conociendo el l azo d e
histéresis y el volumen del material.
Ph
= lazo de histéresis
ciclo ⋅ m 3 ∫
Para c onocer l a ene rgía en l a uni dad de t iempo, hay que m ultiplicar p or l a
frecuencia.
Wh = ∫ lazo de histéresis × frecuencia
STEINMETZ en f orma experimental determina la cantidad de calor producida en 1
cm3 del material:
ΔPh = η ⋅ f ⋅ B máx.
1,6
erg /s.cm3
En tecnología se emplea la misma fórmula modificada:
- 14 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
η ⋅ f ⋅ B máx.
ΔPh =
γ
1,6
⋅ 10 − 4 W/Kg
γ = peso específico del material ferro magnético.
η = coeficiente de histéresis.
Para inducciones muy bajas el exponente de 1,6 tiende a 2.
En la expresión se ve que el exponente de B varía de 1,6 a 2 y la frecuencia esta
elevada a la 1.
Pérdidas por corrientes parásitas o de Foucault
Supongamos tener un cubo de material, de una determinada masa y que
sometemos a un campo magnético longitudinal. Como consecuencia de este campo se van
a enge ndrar c orrientes parásitas qu e v an a t ratar de p roducir un campo m agnético
antagónico.
Figura 12
O s ea pequeñas e spiras en cortocircuito qu e g eneran un a f uerza electromotriz
inducida ex = -dF / dt, que hace circular a la corriente en el núcleo provocando calor.
Estas corrientes serán proporcionales a la inducción, a la frecuencia e inversamente
proporcional a la resistividad de volumen del material ρ.
i = B⋅
f
ρ
si se quiere calcular la potencia de pérdida que provocan esas corrientes:
P=
B2 ⋅ f 2
B2 ⋅ f 2
l
B2 ⋅ f 2
Vatios/Volumen
⋅
=
⋅
⋅
⇒
=
⋅
R
ρ
P
K
s
ρ
ρ2
ρ2
Aquí puede v erse que l as p érdidas son p roporcionales a B 2 y f 2. U na f orma d e
reducir es tas pér didas consiste en s ubdividir el m aterial ( laminándolo o pul verizándolo) de
modo de reducir el valor de las corrientes inducidas o parásitas.
STEINMETZ, con otra fórmula empírica para su cálculo:
- 15 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
ΔPF = ε ⋅ f 2 ⋅ B m
2
erg./s.cm3
o bien
ΔPF =
ε ⋅ f 2 ⋅ Bm
2
γ
⋅ 10 − 4 Vatios/Kg.
γ = peso específico del material.
ε = coeficiente de corriente de Foucault.
En la práctica se determinan en conjunto por la suma de ambas, (con un vatímetro).
ΔPT = ΔPh + ΔPF
determinado espesor.
se ex presa e n v atios por K g. de chapa magnética de u n
Ejemplo: para laminación tipo "A" de 0,35mm de espesor es de 1,7 W/Kg. medidas
con una inducción de B = 10 Kg y una f = 50 Hz.
0,35 mm es el espesor común en nuestros transformadores en electrónica.
También se suministran gráficos doble logarítmicos, para distintas frecuencias.
Gráfica para un solo tipo de material y espesor
Figura 13
Para s eparar l as pér didas, s e r ealizan l as m ediciones c orrespondientes c on l a
inducción B constante, pero con dos frecuencias diferentes f. La inducción magnética en el
material e s directamente pr oporcional a l a t ensión de al imentación V e i nversamente
proporcional a l a f recuencia f . P or l o t anto pa ra m antener l a condición E = Cte., v ariamos
simultáneamente V y f. En ese caso las pérdidas totales dependen únicamente de f 1o que
se deduce de ambas fórmulas de STEINMETZ.
ΔPT = ΔPh + ΔPF = k 1 ⋅ f + k 2 ⋅ f 2
las pérdidas correspondientes a un ciclo:
ΔPT
= k1 + k 2 ⋅ f
f
- 16 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
η ⋅ Bm 1,6
k1 =
⋅ 10 − 4
γ
ε ⋅ Bm 2
k2 =
⋅ 10 − 4
γ
Midiendo las pérdidas con dos frecuencias diferentes f1 y f2, se calculan η y ε, o sea
dos ecuaciones con dos incógnitas, (sistema perfectamente resoluble).
Efecto pelicular magnético
El c ampo a ntagónico que s e pr oduce obl iga a un c onsumo ex tra de e nergía
eléctrica para pasar de un punto a otro del ciclo de histéresis. Por ejemplo para pasar de A,
a B.
Figura 14
Las propiedades magnéticas también se ven modificadas por:
•
Distintos esfuerzos mecánicos, tracción, compresión, etc.
•
El maquinado.
•
La temperatura, (ya vimos punto Curie).
Figura15
Se ha comprobado que, cuando el t amaño del grano s e i ncrementa, l as pé rdidas
por histéresis di sminuyen por consiguiente or ientándola l os g ranos e n f orma p aralela, e n
- 17 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
vez de es tar al az ar, s e obt iene muy al ta permeabilidad y baj as pérdidas p or hi stéresis,
estos materiales reciben nombres comerciales tales como Hipernik, Permendur, etc.
Descripción y clasificación de materiales magnéticos
Los tres más característicos son el Fe, Ni y Co.
El F e pur o e s l o m ejor, p ero sumamente c aro en l aboratorio s e han obt enido mi de ha sta
250.000 ó más. Generalmente no se lo utiliza solo debido al costo de purificación.
El N íquel e s de l os t res el que t iene c aracterísticas menos p ronunciadas, ex cepto p ara l a
fabricación d e componentes magneto r esistivos. Debido a la naturaleza de los f enómenos
magnéticos, í ntimamente l igados con l a es tructura cristalina, l os materiales m agnéticos pr esentan
direcciones preferentes p ara l as c aracterísticas o A nisotropía. A nisotropía = propiedades en u na
dirección.
Forma de la curva o lazo de histéresis
Se pued en producir m ateriales m agnéticos, que tengan cualquier f orma de l azo de
histéresis para cada aplicación en particular, ya sea materiales puros o aleaciones con tratamiento
térmico o mecánico adecuado.
Ejemplo de materiales con distintos lazos de histéresis
Para l a c onstrucción de u n i nductor, que deba m antener l a i nductancia c onstante
para distintos valores de corriente que por el circulen (se verá más adelante el diseño). Una
vez f ijada l as di mensiones f ísicas l a L es di rectamente pr oporcional a l a per meabilidad y
para ello es necesario un lazo que tenga un m constante.
Hay materiales como el "Perminvar", (50% Fe-50% N i), que mantiene constante la
pendiente en un rango de 0 a 2 Amperios . espiras / metro y el lazo es:
Figura 16
Si se representa a μ en f(H) para el mismo material:
- 18 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Figura 17
El μi (permeabilidad i nicial), s e m antiene constante ha sta un os 2 A .v/m, des pués
crece, alcanza un máximo y decrece cuando llega a la saturación. Es importante remarcar,
que la zona utilización es la de m constante. En muchos materiales fuera de esa zona el
lazo toma forma muy irregulares.
El Permalloy se graficó para comparar y decir que su mi es mucho mayor que el del
Perminvar, p ero el del Permalloy en ni ngún m omento mantiene a l a permeabilidad
constante.
Para equipos de audio también anda bien el Perminvar.
Para construir un transformador de alimentación, el volumen del núcleo depende en
forma inversa de la inducción, esto nos lleva a buscar materiales que admitan una elevada
inducción de saturación Bs.
Hay muchos materiales que cumplen con esto, pero hay que hacer un balance entre
costo y volumen.
Figura 18
Lo que se utiliza comúnmente debido a su costo accesible es el Fe - Si (3 a 4% de
Si), no c onviene s uperar el 4, 5% de S i por que se t orna qu ebradizo y s e di ficulta e l
maquinado. E1 ciclo de histéresis indica que el gasto de energía eléctrica es mayor que con
el Permalloy pero su costo es mucho menor.
Para pot encias en el orden de l os cientos de V olt - Amper se alcanza c on F e - Si
rendimientos del orden del 90% o más.
Para i manes permanentes: el hecho de s er destinados a t al efecto, s e encuentran
sometidos a su propio campo des imanador y a la acción eventual de causas externas des
imanadoras hace q ue para qu e e stos materiales pu edan s er utilizados c omo tales, d eban
presentar una fuerte resistencia a la desimanación, es decir altos campos coercitivos. Para
lograrlos, la teoría indica que es necesario que en el material se hallen presentes tensiones
- 19 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
internas t an grandes c omo s ean po sibles e i r r egularmente di stribuidas, al m ismo t iempo
esas macro inclusiones ocupan un gran volumen relativo.
Este endurecimiento magnético, que se produce a causa de ciertos factores, que no
siempre p rovocan al m ismo t iempo u n endu recimiento m ecánico, s e consigue en l íneas
generales, mediante los siguientes procedimientos:
- aceros endurecidos por temple.
- aleaciones endurecidas por dispersión.
- aleaciones endurecidas por deformación.
- aleaciones endurecidas, mediante la formación de súper redes.
Para i manes per manentes o p ara l as ant eriores memorias de núc leos m agnético
usadas en c omputadoras, ( actualmente r eemplazadas p or l as bur bujas m agnéticas d el
inglés Bubble memories y por las seudo RAM), los ciclos son casi cuadrados y esto exige un
gasto de en ergía a dicional, per o el f ormato del l azo es v entajoso p ara l as f unciones a
cumplir.
Figura 19
Si bi en e s c ierto qu e, l as m emorias de nú cleos ha n s ido r eemplazadas, s e va a
detallar sus conceptos, con el objeto de poder hacer uso de ella en alguna otra aplicación,
(control, automatización, etc.).
Supongamos un núc leo c on l azo c omo l o i ndica l a f igura ant erior, ( elevada
retentividad o remanencia y elevada fuerza coercitiva y que va a ser usada como memoria
de u n bi t, ( llamase bi t a l a c élula básica de m emoria qu e pu ede t ener do s estado un o o
cero).
Figura 20
- 20 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Los dos estados estables del núcleo son Br y -Br.
Si se aplica un pulso de excitación hasta el valor Hmáx o -Hmáx, al retirar la excitación
el núcleo vuelve al valor estable Br o -Br respectivamente.
Para saber si s e e ncuentra en B r o –Br, s e aplica un pul so de v alor H máx, si s e
encuentra en el punto 1, debido a la excitación pasa a 2 y al retirarla (Hmáx) vuelve a 1. En
estas condiciones la variación de B al pasar de 1 a 2 y retornar a l da un ΔB ≈ 0.
Supongamos ahora que hubiera estado en -Br y se aplica un pulso Hmáx pasará de 3
a 2 y al quitar el pulso pasará de 2 a 1, es decir pasa de -Br a +Br, en este caso ΔB = / 2 Br /
y la tensión inducida vale Eind. Eind = 4,44.f.N.S. ΔB.10-8 (Volt eficaces). Si esto forma parte
de un circuito que de alguna m anera s e pu edan d etectar l as v ariaciones d e i nducción, el
sistema forma parte de una memoria de 2 estados, capaz de retener la información cuando
se corta la alimentación al sistema.
En la figura se ven tres conductores, uno cumple la función de emitir +Hmáx o -Hmáx,
el s egundo e s el que env ía úni camente + Hmáx y el tercero e s el que l leva l a i nformación,
terminales Write, Read y bit de memoria respectivamente. El sistema trabaja por variaciones
de B que dan dos niveles de tensión, (1 o 0).
En la actualidad las memorias de núcleos han sido reemplazadas por las
mencionadas bubble memories, donde se logra 1.600 bits/mm2 y chips que contienen hasta
20.000 bits. Se estima llegar rápidamente a 100.000 bit/mm2.
La c aracterística f undamental par a el i mán pe rmanente es l a m isma qu e pa ra l a
memoria d e núcleo, el evada i nducción r emanente Br y el evada f uerza coercitiva H c, par a
ello definamos al:
Producto de Energía Especifica (PEE)
El tramo de lazo de histéresis comprendido en el segundo cuadrante de la figura
Figura 21
nos permite evaluar el comportamiento de un i mán, ya que i ndica la B que es e imán es capaz de
proporcionar en pr esencia de un campo m agnético d esmagnetizante. E ste c ampo m agnético
desmagnetizante, (desimanador), puede ser un campo real o puede ser el efecto equivalente de un
entre hierro, en el que para p roducir u na i nducción dada, el i mán de be " superar" u n v alor d e l a
intensidad de c ampo det erminada po r l a l ongitud del ent re hi erro. E l pr oducto de l os H i. B i en un
punto c ualquiera de l a c urva B -H r epresenta l a energía m agnética p roporcionada en es as
condiciones por el imán, (por unidad de volumen). Si a la derecha de la parte del lazo de histéresis,
(1º cuadrante), graficamos punto a punto el valor del producto B.H, obtenemos el gráfico anterior. El
valor m áximo del pr oducto B .H s e l lama " Producto de en ergía E specífica", ( energy - product) y
constituye un índice muy adecuado par a ev aluar materiales m agnéticos par a ut ilizarlos c omo
imanes, su valor esta dado en Joule/m3. La siguiente tabla ilustra características al respecto.
- 21 –
TECNOLOGÍA ELECTRÓNICA
Material
Acero 1% C
Acero 6% W
Acero 6% Co
Acero 35% Co
Alnico III
Ticona1 G
Alnico VB
F.R.M. - U.T.N.
PEE (Joule/m3) Br (wb/m2)
2.000
0,9
3.000
1,0
4.400
0,75
5.300
0,9
17.000
0,8
55.000
1,35
75.000
1,35
Tabla 4
Hc (A.v/m)
4.000
2.200
11.600
20.000
50.000
52.0000
60.000
Composición
99 Fe, 1 C
92,2 Fe; 6 W; 0,9 C; 0.1 Co
82 Fe; 6 Co; l,5 W; 1,5 C
51,15 Fe; 35 Co; 9 Cr; 4 W
51 Fe; 24 Co; 14 Ni; 8 Al; 3 Cu
48 Fe;24 Co;l4 Ni; 8 Al; 6 Cu.
48 Fe;24 Co;14 Ni; 8 Al; 6 Cu.
Figura 22
El primero de la tabla casi no se usa.
Actualmente se pueden fabricar en forma de pequeñas longitudes y gran sección, debido a
las bondades de las aleaciones que figuran en la tabla.
Supongamos un parlante en que v amos a em plear u n i mán per manente. E l c ircuito
magnético posee un núcleo cilíndrico central y en el entre hierro se encuentra la bobina móvil.
Figura 23
Las piezas polares s on de hierro dulce, s e ut iliza para f acilitar las f ormas, es de más f ácil
maquinado y de llevar a tolerancias adecuadas, (en un parlante de alta calidad el entre hierro es de
1 mm). El imán tiene forma de pastilla y se cierra el circuito magnético como lo indica la figura. De
este modo el imán solo requiere dos caras terminadas, (o sea menos sometimiento al maquinado,
ya que esto le cambia las características).
Actualmente se lo puede magnetizar una vez hecho el montaje definitivo.
Ferritas para Imanes Permanentes
Se pueden producir imanes por medio de óxidos de Fe; Co; Ni; Mn- Zn en polvo sinterizado
a 1. 000 ° C y enf riados en un campo m agnético i ntenso, se obtienen v alores de B .H = 15. 000
Joule/m3. Las ferritas (ferrites) al Bario son producidas por Philips con el nombre de "ferroxdure” y la
- 22 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
fábrica Mullard con el nombre de "Magnadur" etc. el B.H tiene un valor doble al correspondiente a
los imanes sinterizados con óxidos de hierro y cobalto.
Los óxidos pulverizador se comprimen en pr esencia de un c ampo magnético y los imanes
se dejan enfriar en presencia de un campo magnético. Estas ferritas se distinguen por un valor muy
elevado d e f uerza coercitiva H c = 1 70.000 p or l o que s on i nsustituibles e n l os c asos que existen
campos desmagnetizantes intensos. Poseen por otra parte una resistencia óhmica muy elevada con
P superior a 107 W/cm.
Cintas Magnéticas
La cinta está constituida por una película de Acetato de Celulosa, Tereftalato de polietileno
(mylar) o PVC, sobre una o ambas caras se deposita una capa de barniz que contiene óxido de Fe.
El óxido de Fe rojo Fe2O3 tiene propiedades magnéticas y puede cristalizar en el sistema cúbico o
rectangular, que son l as formas m ás adecuadas p ara l a f abricación de cintas m agnéticas c on l a
condición, de que la orientación sea en el mismo sentido de deslizamiento de la cinta. La orientación
se obtiene por medio de un campo magnético que se somete cuando aún el barniz está líquido. La
calidad d e l a depo sición i nfluye, s obre ; . l a s ensibilidad, uni formidad, r esistencia al uso, m ínima
tendencia a la producción de cargas estáticas, etc.
Hay ot ras cintas f abricadas con Dióxido de Cromo, que at enúa en g ran par te e stos
inconvenientes.
Los espesores d e l as cintas e stán e ntre 0, 02 y 0,04 m m. L a c elulosa se env ejece m ás
rápido, pero cuando se rompe lo hace con corte neto, en cambio el mylar lo realiza con un corte con
deformación plástica.
Cerámicas Magnéticas
Para el u so de audi o f recuencias, r adio f recuencias y aún en es pectro de l as m icroondas
(l.000 MHz ó más), se utilizan los llamados "micro polvos”, que consisten en obtener por medio de
materiales magnéticos pulverizados y luego c ompactados c on r esinas es peciales c on distintas
formas po r medio d e m oldeo, cuyos gr ánulos e stán ent re 10 y 20 m icrones. A nteriormente l os
polvos del material se obtenían por desgaste o pulido. Actualmente se los obtiene por precipitación
química, (electrólisis).
Otros materiales se los obtiene por combinación de
Fe2 O3 + Ni + Zn + Co + Mn
que debido a la cristalización cúbica y alta resistividad se las conoce con el nombre generalizado de
“cerámicas magnéticas”. Para el caso de los micro polvos la permeabilidad está, en el orden de 150
a 200 y una Bs de 2.000 a 4.000, el lazo es como del tipo I.
Figura 24
- 23 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Pese a la forma de su lazo, debido a las pequeñas partículas de material que lo constituye,
las pérdidas son pequeñas. La gráfica II, corresponden a las cerámicas magnéticas que al tener un
Bs no elevado restringe su uso.
Método
Obtención
Dureza
Densidad
Bs
Resistividad
Fuerza
Coercitiva
sólidas.
Tabla Comparativa
Laminado de Bajas
Ferritas
Micro Polvos
Pérdidas
Imanes
Núcleos
Imanes
Núcleos
Imanes
Núcleos
de Laminaciones al eaciones Productos s interizados y Materiales uni dos y
sólidas
moldeados
moldeados
Duros
Blandos
Duros
Duros
Blandos
Blandos
7a8
Ídem
4a5
4a5
5a7
Kg/dm3
Alta
Alta
Baja - Media
Bajas
Bajas
Muy Altas
Medias
Baja
Alta
Medias
Tabla 5
De la tabla se deduce que para transformadores de poder, son convenientes las aleaciones
Para transformadores de entrada, (tensiones bajas), pueden usarse de los tres tipos.
Las ferritas son especiales para bajos valores de B.
Para transformadores de F.I. (tensiones del mV), son buenos los micro polvos y las ferritas.
Los núcleos laminados óptimos hasta 10 Khz. Los micro polvos hasta unos 100 Khz.
Las ferritas hasta 100 MHz, y algunas tal como la soft - ferrites puede trabajar como guía de
onda en microonda (1.000 MHz o más). La magnetita Fe2 O3 Fe O (ferrito ferroso), fue la primera
en conocerse, tres veces mayor resistividad al Fe puro pero menor a las antes mencionadas.
Materiales y Aleaciones para laminaciones
Hierro puro hidrogenado: apto para blindaje magnético, Bs puede llegar a 20.000.Gs.
Acero: Bs de 18 a 20 Kg la Hc = 100 Oe, mientras que el Fe puro es de 100 a 500 Oe. La
permeabilidad es de unos 3.500.
Fundición: Desde el p unto de v ista m agnético e s i nferior a l os otros m ateriales, pe ro l a
ventaja es su bajo costo para aplicaciones industriales.
Cobalto: Bs llega a 10 KGs pero con tratamiento térmico adecuado modifica sus
características magnéticas.
Níquel: Bs es menor al Co, con tratamiento mecánico varían sus propiedades magnéticas.
Las impurezas en todos los casos son perjudiciales, tales como el fósforo, azufre, etc.
Aleaciones: Lo más común para transformadores el Fe - Si, el Si mejora las características
del Fe, con el porcentaje de Sí aumenta la resistividad, de e sta manera se reducen enormemente
las corrientes inducidas.
Tabla que muestra la influencia del Si
- 24 –
TECNOLOGÍA ELECTRÓNICA
% de Si
1,25
2,75
3,25
4
F.R.M. - U.T.N.
ρ (μ.Ω.cm)
28
43
50
60
Tabla 6
Pérdida W/Kg. a 10 KGs. y 50 Hz
1,5 a 2
1,25 a 1,35
1,0 a 1,25
0,7 a 0,8
No conviene superar el 4,5% de Si, por cuanto se torna quebradizo y es inconveniente para
el maquinado.
Fe - Si de Grano Orientado
Consiste e n recocer a l a aleación l levándola a t emperatura de ablandamiento y en e stas
condiciones someterla a un intenso campo magnético, luego enfriarla en presencia de ese campo.
En el comercio s e l as conoce por el n ombre d e f ábrica, po r ej emplo el " hispersil" de 0,5
W/Kg. de pérdidas. La gráfica da la mejora con respecto a la aleación común de Fe - Si.
Figura 25
Figura 26
La f orma de núc leo r ealizado c on 4 I, t iene 4 j untas en l ugar de 2 d e l a E -I, p ero s e
compensan las pérdidas porque la orientación del grano va siempre en la dirección de las líneas de
flujo.
- 25 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Núcleos para Inductores y Transformadores con cinta arrollada.
Figura 27
Este p rocedimiento e s m ás costoso q ue l a l aminación c omún, pero a veces se justifica
porque de e sta f orma p ermite el bo binado en m áquinas c omunes l uego el r esultado final es
equivalente al toroide. La forma toroidal es codiciada porque es la única forma que confina al campo
magnético sin entre hierro o juntas. Los flejes pueden ser de "Permalloy" (Fe-Ni) del orden de 0, 02
mm de espesor, o de grano orientado, etc.
Cazoletas
Dada l as di ficultades d e bobi nar nú cleos t oroidales, s e c onstruyen nú cleos p ulverizados o
de ferritas.
Desde el pu nto de v ista t opológico e s a l a i nversa del t oroide, porque en l a c azoleta e l
bobinado va centro del núcleo, con las siguientes ventajas:
1º- la bobina es de tipo convencional, se bobina en máquinas comunes.
2°- El bobinado se encuentra totalmente encerrado y queda protegido por eventuales daños
como en el toroide convencional.
3º- Permite c alibración. debi do al entre hierro, hace que el núc leo a r osca s e pueda
desplazar dentro de ciertos límites. E1 toroide convencional no lo tiene.
4°- Permite montarse en plaqueta impresa mediante brida de sujeción.
Figura 28
Laminación E-I
Es quizás la más utilizada y se fabrica en la forma llamada sin desperdicio, si se mantienen
las siguientes relaciones:
- 26 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
Figura 29
En el comercio las medidas se designan de la siguiente forma:
Figura 30
Otros formatos comunes de laminación:
Figura 31
- 27 –
TECNOLOGÍA ELECTRÓNICA
F.R.M. - U.T.N.
BIBLIOGRAFÍA
•
•
MAGNETIC MATERIALS AND THEIR APPLICATIONS-Carl Heck-Ed. Butterword.
SOFTFERRITES, PROPERTIES AND APLICCATIONS-E. Snelling -Ed.ILIFFE.
- 28 –