Teorías estadísticas para la descomposición unimolecular
Anuncio

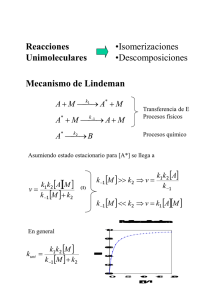
TEORÍAS ESTADÍSTICAS DE DESCOMPOSICIÓN UNIMOLECULAR José G. López, Gloria Moyano Teoría de la Dinámica de Reacciones Químicas Instituto de Química Universidad de Antioquia Medellín Predicción de Coeficientes de Velocidad Métodos empíricos Relaciones con coeficientes de velocidad ya medidos de reacciones similares Métodos de dinámica Predicción basada en seguir explícitamente el movimiento de los átomos en el tiempo. Precisión perfecta en principio (dinámica cuántica) Puede ser costosa a nivel computacional Teorías estadísticas Realiza suposiciones sobre las escalas de tiempo del flujo de energía intramolecular y de reacción. Teoría del Estado de Transición (TES) y sus extensiones Teoría RRKM para reacciones unimoleculares Teoría del Estado de Transición Canónica Suposiciones Aproximación de Born-Oppenheimer a las moléculas reactantes Distribución de Boltzmann para las moléculas reactantes Superficie divisoria en el punto de silla. Una vez el par de moléculas reactantes la ha cruzado, no puede retornar En el punto de silla el movimiento a lo largo de la coordenada de reacción no está acoplado con los otros movimientos En el estado de transición la distribución de Boltzmann sigue describiendo los estados internos de las moléculas reactantes A + B → X ≠ →C ≠ k T Q k (T ) = L≠ B e − E0 / kBT h QAQB Teoría del Estado de Transición Microcanónica Ideas básicas Cálculo de coeficientes de velocidad para una colección de moléculas todas con la misma energía (colectivo microcanónico) TET canónica: funciones de partición TET microcanónica: suma ó densidad de estados ∞ k (T ) = ∫ k ( E ) P ( E , T )dE 0 Suma y Densidad de Estados Molécula de N átomos con Hamiltoniano H(p,q) y s grados de libertad Volumen de espacio de fases clásico con enegía máxima E Vs = ∫ H =E H =0 ∫ dp … dp dq … dq 1 s 1 s Número (suma) de estados, G(E), en el rango de energía 0 a E V 1 G ( E ) = ss = s h h ∫ H =E H =0 ∫ dp … dp dq … dq 1 s 1 s Número de estados, W(E), en el rango E → E + dE 1 W (E) = s h ∫ H = E + dE H =E ∫ dp … dp dq … dq 1 s 1 s Densidad de estados, N(E) N (E) = dG ( E ) W ( E ) 1 = = s dE dE h ∫ ∫ dp … dp dq … dq H =E 1 s 1 s Suma y Densidad de Estados N(E): Número de estados en un intervalo pequeño δE dividido por δE E G(E): Número de estados por debajo de E ¿Qué es una Reacción Unimolecular? Un solo reactivo está involucrado en la reacción elemental Disociación C2H5Cl → HCl + C2H4 Isomerización ciclopropano → propileno Cinética química A → productos constante de velocidad unimolecular − d [A] = kuni [A] dt [A] = [A]0 e − kt ¿Por qué ocurre? Hipótesis de la radiación La energía para la reacción proviene de las paredes del recipiente en forma de radiación La reacción debe ser de primer orden en todo rango de presión Activación por colisiones La energía para la reacción proviene de colisiones con otras moléculas La reacción es de primer orden a altas presiones La reacción es de segundo orden a bajas presiones Mecanismo de Lindemann–Christiansen k1 → A∗ + M A + M ← k−1 k2 A∗ → productos kuni k1k2 [M] = k−1[M] + k2 Si la presión es alta − d [A] k1k2 = [A] dt k−1 kuni → k∞ = k1k2 k−1 Si la presión es baja d [A] − = k1[A][M] dt kuni → k0 = k1[M] Mecanismo de Lindemann–Christiansen kuni k∞ se mide experimentalmente k∞ = k∞ 1+ k1[M] k1 se determina usando el modelo de colisiones de esferas duras reactivas k-1 es igual a la velocidad de colisión σ v k2 es independiente de E 1/2 8k T Z1 = B π d 2 πµ k∞ kuni E0 k1 = Z1 exp − k T B Experimental Teórico [M] Modificación de Hinshelwood Movimiento interno vibracional de A contribuye a la energía para formar A* Molécula A conformada por s osciladores armónicos clásicos acoplados Probabilidad de una molécula A con energía mayor que E0 aumenta con s k2 independiente de E Z1 E0 k1 = ( s − 1)! k BT ss−1 −1 E0 exp − k T B Número de osciladores s necesarios → mitad del número de modos vibracionales Gran dependencia con la temperatura en el factor preexponencial, especialmente a altos valores de s Teoría RRK Clásica RRK = Rice - Ramsperger - Kassel Todos los estados internos de A* a la energía E son accesibles Redistribución de la energía vibracional dentro de la molécula (IVR) más rápida que la reacción Probabilidad que una molecula con s osciladores clásicos con energía total E tenga una energía mayor que E0 en el modo vibracional que conduce a la reacción (osciladore crítico) k2 cambia con E. k2 → k2(E) ≡ k(E) k-1 es igual a la velocidad de colisión Permitir diferentes velocidades de producción de A* con diferente E dk1 ( E ) ∗ → A + M ← A ( E , E + dE ) + M k−1 k (E) A∗ ( E , E + dE ) → productos Teoría RRK Clásica E − E0 k (E) = ν E s −1 dk1 ( E ) 1 E = k−1 ( s − 1)! k BT ∞ kuni = k ( E ) dk1 ( E ) k−1 ∫E k (E) 0 1+ k−1[M] kuni = ν e−b ∞ 0 ν frecuencia vibracional del oscilador crítico ω frecuencia de la colisión = k-1 [M] E0 energía de activación a altas presiones número de osciladores efectivos E exp − k BT ( s − 1)! ∫ E − E0 x= RT s s −1 dE k BT x s −1e− x 1+ ν x ω b + x E0 b= RT s +1 dx dE dx = RT Teoría RRK Cuántica j !( j − m + s − 1)! k (E) =ν ( j − m)!( j + s − 1)! j numero total de cuantos disponibles = E/hν m número requerido en el oscilador crítico para la reacción = E0/hν kuni k∞ − ( j −m ) hν / kBT ( j − m + s − 1)! e ∞ ( j − m)!( s − 1)! − hν / k BT = [1 − e ]∑ ν j !( j − m + s − 1)! j =m 1+ ω ( j − m)!( j + s − 1)! ( ) ν factor preexponencial experimental a altas presiones m = Ea∞/hν s = 3N - 6 k∞ = ν e − E0 / kBT Teoría RRKM Uso de TST para evaluar k2(E) = k(E) Modos vibracionales y rotacionales de A* y A≠ considerados activos Teoría microcanónica del estado de transición Mecanismo de disociación o isomerización de A*: k(E) A∗ → A ≠ → productos Suma de estados del complejo activado con energía E≠ = E – E0 – Er 1 G(E ≠ ) k (E) = h N ( E − Er ) Densidad de estados del reactivo con energía Ev = E – Er Teoría RRKM N (E) Energía total G ≠ ( E − E0 ) Energía del punto cero del estado de transición Suma de estados del complejo activado con energía E≠ = E – E0 E E0 1 G ≠ ( E − E0 ) k (E) = h N (E) Densidad de estados del reactivo con energía E (Número de estados en un intervalo pequeño δE dividido por δE) Energía del punto cero de la molécula Teoría RRKM 1 G ≠ ( E − E0 ) 1 G ≠ ( E − E0 ) k (E) = → k (E) = σ h N (E) h N (E) Degeneración de la reacción (σ) Deneración en el cálculo de sumas y densidades de estado Evaluación basada en los números de simetría del reactivo (σr) y del estado de transición (σ≠) σ= σr σ≠ Número de simetría: número de orientaciones indistinguibles debida a rotaciones apropiadas Programa RRKM1 Programa para calcular constantes de velocidad unimoleculares 1L. Energía total molecular E Momento angular Correcciones anarmónicas Zhu and William L. Hase, Quantum Chemistry Program Exchange, QCPE No. 644 Archivo de Entrada Programa RRKM STANDARD CALCULATION Triflorometano 69.4,0.1,20, 0, 10,1,1,300, 0, 0, 0, 1.0, 9,0 1188,1188,1067,760,548,548,350, 305,305, 241,241,46.14, 0, 69.4, 8,0 1188,1188,1067,760,548,548,75, 75, 482.,482.,46.14 0, !linea titulo !linea titulo !EMIN(kcal/mol),DE,NE !JMIN,DJ,NJ,TROT !SIGMA(factor estadistico) !NF,NR (molecula) !freq. vib. molecula !Momentos inercia molecula !E0 !NF,NR (estado transicion) !freq. vib. estado trans. !Momentos inercia estado trans. Resultados E J KCAL/MOLE 69.40 69.50 69.60 69.70 69.80 69.90 70.00 70.10 70.20 70.30 70.40 70.50 70.60 70.70 70.80 70.90 71.00 71.10 71.20 71.30 DENSITY SUM 1/CM-1 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 10 0.1449D+08 0.1464D+08 0.1479D+08 0.1494D+08 0.1510D+08 0.1525D+08 0.1541D+08 0.1557D+08 0.1573D+08 0.1589D+08 0.1605D+08 0.1621D+08 0.1638D+08 0.1654D+08 0.1671D+08 0.1688D+08 0.1705D+08 0.1722D+08 0.1739D+08 0.1757D+08 RATE CONSTANT SECOND-1 0.0000D+00 0.3677D+02 0.5641D+02 0.7464D+02 0.9547D+02 0.1195D+03 0.1471D+03 0.1788D+03 0.2152D+03 0.2566D+03 0.3036D+03 0.3569D+03 0.4171D+03 0.4847D+03 0.5606D+03 0.6455D+03 0.7402D+03 0.8456D+03 0.9627D+03 0.1092D+04 0.0000D+00 0.7528D+05 0.1143D+06 0.1497D+06 0.1896D+06 0.2348D+06 0.2862D+06 0.3444D+06 0.4102D+06 0.4842D+06 0.5672D+06 0.6601D+06 0.7635D+06 0.8785D+06 0.1006D+07 0.1147D+07 0.1302D+07 0.1472D+07 0.1659D+07 0.1864D+07