Reglas representación gráfica
Anuncio
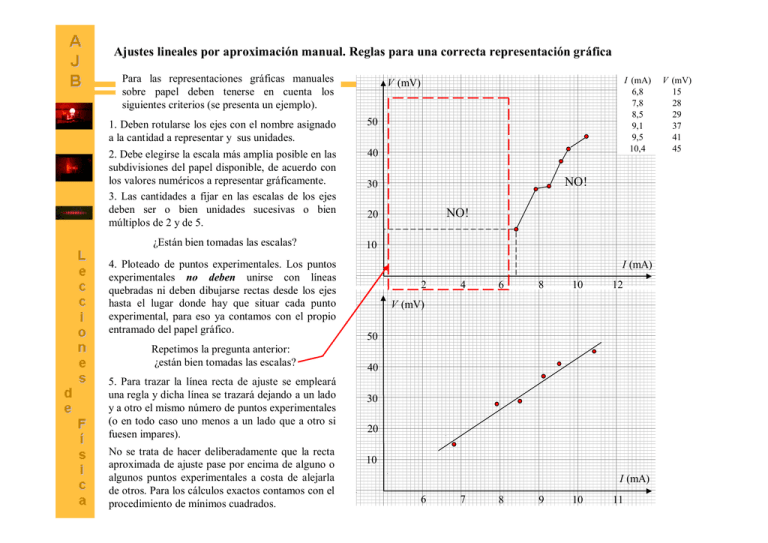
Ajustes lineales por aproximación manual. Reglas para una correcta representación gráfica Para las representaciones gráficas manuales sobre papel deben tenerse en cuenta los siguientes criterios (se presenta un ejemplo). 1. Deben rotularse los ejes con el nombre asignado a la cantidad a representar y sus unidades. 50 2. Debe elegirse la escala más amplia posible en las subdivisiones del papel disponible, de acuerdo con los valores numéricos a representar gráficamente. 3. Las cantidades a fijar en las escalas de los ejes deben ser o bien unidades sucesivas o bien múltiplos de 2 y de 5. 40 30 ¿Están bien tomadas las escalas? 10 4. Ploteado de puntos experimentales. Los puntos experimentales no deben unirse con líneas quebradas ni deben dibujarse rectas desde los ejes hasta el lugar donde hay que situar cada punto experimental, para eso ya contamos con el propio entramado del papel gráfico. Repetimos la pregunta anterior: ¿están bien tomadas las escalas? 5. Para trazar la línea recta de ajuste se empleará una regla y dicha línea se trazará dejando a un lado y a otro el mismo número de puntos experimentales (o en todo caso uno menos a un lado que a otro si fuesen impares). No se trata de hacer deliberadamente que la recta aproximada de ajuste pase por encima de alguno o algunos puntos experimentales a costa de alejarla de otros. Para los cálculos exactos contamos con el procedimiento de mínimos cuadrados. I (mA) 6,8 7,8 8,5 9,1 9,5 10,4 V (mV) NO! NO! 20 I (mA) 2 4 6 8 10 12 V (mV) 50 40 30 20 10 I (mA) 6 7 8 9 10 11 1 V (mV) 15 28 29 37 41 45 Ajustes lineales por aproximación manual. Procesado de la información gráfica. V m I b En el ajuste lineal de nuestro ejemplo tenemos que obtener la relación entre el voltaje y la intensidad, la cual tendrá la forma y m xb V (mV) 50 48 40 N 48 13 35 mV N 1 1 2 mV 30 20 D 10.6 6.4 4.2 mA 13 D 0.1 0.1 0.2 mA 6.4 10.6 I (mA) 6 m 7 8 N 35 mV 8.3333 8.3333 D 4. 2 mA m m m N D N D m Ordenada origen Pendiente A. Determinación de la pendiente m 10 I (mA) 6,8 7,8 8,5 9,1 9,5 10,4 9 10 11 (decimales a ajustar posteriormente) 1 N N 2 D D D El resultado para la pendiente debe expresarse con tantas cifras significativas como sea preciso para incluir las décimas: dos en este caso. m V (mV) 15 28 29 37 41 45 Trazamos un triángulo rectángulo cuya hipotenusa es la recta de ajuste manual: los catetos del mismo paralelos a los ejes coordenados y pasando por puntos próximos a los valores extremos de nuestros datos (no es necesario que coincidan exactamente con esos valores extremos). Las longitudes de los catetos N, D se calculan por diferencia. Errores N, D: dependerán de los errores de las medidas experimentales. Como N y D se calculan por diferencia, sus errores se obtienen sumando los errores del minuendo y el sustraendo. Ya que la tabla de medidas experimentales no indica otra cosa, supondremos que el error en cada medida es una unidad del orden decimal más ala derecha. Error absoluto 1 35 2 0.2 0.5 0.4 0.9 Una cifra significativa 4.2 4. 2 2 (décimas en este caso) m 8.3 0.9 Error relativo m 0.9 0.11 (11%) 2 m 8.3 Ajustes lineales por aproximación manual. Procesado de la información gráfica. En el ajuste lineal de nuestro ejemplo tenemos que obtener la relación entre el voltaje y la intensidad, la cual tendrá la forma V m I b B. Determinación de la ordenada en el origen b y m xb V (mV) y 50 40 y0 33 30 20 x0 8.8 x 10 I (mA) 6 7 8 Aplicada a esta elección particular x0, la recta de ajuste cumple que y0 m x0 b 9 Ordenada origen Pendiente 10 11 I (mA) 6,8 7,8 8,5 9,1 9,5 10,4 V (mV) 15 28 29 37 41 45 La ordenada en el origen es el punto de corte de la recta de ajuste con el eje vertical, es decir, el valor de y cuando x = 0. En principio bastaría con prolongar la recta hasta llegar a dicho eje vertical para ver cuál es el valor del punto de intersección. Pero en este caso nuestra gráfica no está escalada desde x = 0 en adelante (recuérdese que esto lo hicimos aplicando el criterio de que la escala debe ser tal que nos ofrezca la gráfica más amplia posible). Por eso no “vemos” el origen de coordenadas (0,0), y calcularemos el valor de b a partir de la información de la que ya disponemos. Tomamos un valor x0 de la abscisa comprendido en el rango de nuestros datos, vemos qué valor y0 de la ordenada le corresponde en nuestra recta de ajuste y calculamos b. Cálculo el error b aplicando la propagación de errores b y0 x0 m m x0 b y0 m x0 b 33 8.3 8.8 40.04 mV b 1 8.8 0.9 8.3·0.1 9.75 10 mV b 40 310 mV Ajustes lineales por aproximación manual. Resultados y discusión. I (mA) 6,8 7,8 8,5 Discusión sobre el resultado. 9,1 El significado físico de la pendiente de la recta de 9,5 ajuste es la resistencia eléctrica de un conductor 10,4 Ecuación de la recta de ajuste de nuestros datos: y V m I b m x b V 8.3 0.9 I 40 10 mV mA mV Comparación con ajuste mínimos cuadrados V 8.3 0.5 I 40 4 V (mV) 15 28 29 37 41 45 óhmico (la diferencia de potencial entre los dos extremos del conductor es directamente proporcional a la corriente que circula por él). La aparición de un término independiente distinto de cero (la ordenada en el origen) puede deberse a un defectuoso ajuste de cero del voltímetro con el que se tomaron las medidas de voltaje. 60 50 40 30 20 10 0 0 2 4 6 8 10 12 -10 -20 -30 -40 -50 Pendiente m = m = Ordenada en origen 8,32685621 0,45586992 Coeficiente de correlación b = b = -39,80486807 3,993959974 r = 0,980644333 4 EJERCICIO Un pequeño ventilador se conecta a una fuente de tensión regulable y se mide su periodo de rotación cuando se le aplican diferentes voltajes, obteniendo los resultados que se presentan en la tabla adjunta. Los voltajes y sus incertidumbres están expresados en voltios, y los periodos y sus incertidumbres están en milisegundos. Se pide: V (Volt) V T (ms) T 6,3 7,1 8,6 10,0 11,7 0,1 0,1 0,1 0,1 0,1 31,90 28,30 23,20 19,89 17,33 0,05 0,05 0,05 0,05 0,05 a) Determinar qué relación cuantitativa existe entre la velocidad angular del ventilador y el voltaje aplicado. ¿Se trata de una relación lineal?. Calcule errores en esta determinación y exprese las unidades pertinentes. b) Determinar cuántas vueltas por segundo daría este ventilador si el voltaje aplicado fuese de 8 voltios. c) Si en cierto momento la velocidad angular del ventilador es 300 rad/s, ¿cuál es el voltaje aplicado? 5






