Tema 10. Propiedades mecánicas: Fatiga y Termofluencia.
Anuncio

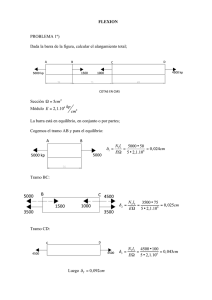
Tema 10 Propiedades Mecánicas: Fatiga y Termofluencia. Fatiga Es la falla por fractura del material que se da cuando se aplican esfuerzos que cambian con el tiempo. Bajo condiciones estáticas (esfuerzo constante) esfuerzos aplicados menores que la Resistencia a la Tensión no harían que el material falle. Sin embargo, si los esfuerzos varían en el tiempo, como por ejemplo el caso de un rótulo sujeto a las fuerzas del viento, la repetición sucesiva de esfuerzos puede causar la falla por fatiga. La falla por fatiga se da en tres etapas: 1. Se genera una grieta muy pequeña en el material. Esta grieta también puede ser un defecto pre-existente originado en la fabricación del mismo. 2. La grieta crece una longitud pequeña cada vez que se aplica un ciclo del esfuerzo. 3. Cuando la grieta ha crecido demasiado, la pieza se debilita y se fractura de manera súbita. Las propiedades de fatiga de un material se determinan por medio de un ensayo de fatiga. Este ensayo consiste en someter al material a un esfuerzo cíclico y contar el número de veces que se aplica el esfuerzo hasta que el material se rompe. El ensayo más común es hacer girar un eje con una fuerza en flexión en uno de sus extremos. 78 Cada vuelta que da el eje es un ciclo de esfuerzo que se aplica sobre él. Para un eje de sección circular cargado tal como muestra la figura anterior se tiene lo siguiente: Esfuerzo aplicado sobre el eje = σ = 10.18 L F d3 donde: σ = esfuerzo aplicado sobre el eje medido en lbs / pulg2 (psi) L = longitud del eje en pulgadas F = fuerza aplicada en flexión en el extremo del eje en lbs. d = diámetro del eje en pulgadas. Se mide cuántas vueltas puede dar el eje sin romperse (ciclos de carga). Cuando finalmente el eje se rompe, se grafica el número de ciclos de carga contra el esfuerzo aplicado. Al repetir el proceso para varios valores de esfuerzo aplicado, se obtiene la curva de fatiga del material. Las curvas de fatiga típicas de los metales tienen dos tendencias bien definidas: los metales ferrosos tienden a una asíntota horizontal mientras que los metales no ferrosos tienen una tendencia decreciente. A partir de la curva de fatiga del material, se obtiene el valor de la Resistencia a la Fatiga del material. 79 σ σ 106 - 108 80 σ La vida de fatiga es el número de ciclos (o tiempo) que un material puede resistir al esfuerzo aplicado antes de romperse. Las propiedades de fatiga son sensibles a las muescas que tenga la pieza y a los defectos de su superficie. Termofluencia. En un metal a temperatura ambiente, un esfuerzo aplicado menor que σy no produce deformación plástica. Sin embargo, si la temperatura del metal se incrementa, es posible que comience a deformarse plásticamente aún cuando los esfuerzos aplicados sean bajos. Esta deformación plástica depende de la temperatura y del tiempo que la fuerza esté aplicada. La Termofluencia es la deformación plástica que puede sufrir un material a temperatura elevada y durante períodos largos de tiempo aún cuando el esfuerzo aplicado sea menor que su Resistencia a la Fluencia (σ < σy). La Termofluencia es causada por el movimiento de las dislocaciones, las cuales ascienden en la estructura cristalina a causa de la difusión. La dislocación no se mueve sobre su plano de deslizamiento como sería el caso de la deformación plástica causada por una fuerza mayor que σy, sino que se mueve perpendicular a su plano de deslizamiento. 81 El que la dislocación se mueva, se traduce en que el material se deforma plásticamente. La Termofluencia es un fenómeno que depende significativamente de la difusión. ∆E / ∆t Tiempo de ruptura tr Debido a que la Termofluencia es activada por la difusión, responde a la ecuación de Arrhenius: 82 Rapidez de termofluencia = Cσ n exp(− Tiempo de ruptura = Kσ m exp( Qc ) RT Qc ) RT C, K, m y n son propiedades del material. La termofluencia también puede describirse por medio de las curvas de esfuerzo – ruptura. σ (escala log) Tr (h) (escala log) Las curvas de esfuerzo – ruptura para diferentes temperaturas pueden describirse por medio del parámetro de Larson – Miller, el cual se define de la siguiente forma: LM = ( T/ 100) (A + B ln t) donde: A y B: constantes del material T: temperatura t: tiempo 83 PROBLEMAS (1) Se sabe que una aleación de bronce tiene un esfuerzo de fluencia (σy) de 240 MPa, una resistencia a la tensión (σu) de 310 MPa, y un módulo de elasticidad de 11 x 104 MPa. Una barra cilíndrica de 15.2 mm de diámetro y 20 cm de largo es fabricada con esta aleación, y luego sometida a una fuerza en tensión, encontrándose que mientras la fuerza está aplicada la barra se deforma 1.9 mm. En base solamente a la información proporcionada, ¿Es posible calcular la magnitud de la fuerza que se requiere para producir la deformación? Si es posible, calcule la fuerza. Si no es posible, explique por qué no es posible. (2) Se utilizará un alambre de acero de 5 milímetros de diámetro para levantar un peso. El alambre estará en tensión y debe resistir una fuerza de 9817 N sin sufrir deformación plástica. Usted consulta en la ferretería y le ofrecen alambre fabricado a partir de los siguientes aceros: 1020, 1040 y 1080 todos en la condición “as-rolled”. ¿De cuál o cuáles aceros debe estar fabricado el alambre? (3) El alambre seleccionado en el problema anterior debe correr sobre una polea también de acero. La fricción entre el alambre y la superficie de la polea provocará desgaste en los materiales. El diseño requiere que la polea sea la que sufra el desgaste, y que éste (el desgaste) sea el menor posible. Usted va a la ferretería y le ofrecen tres poleas fabricadas por tres empresas distintas. La polea 1 tiene una dureza Rockwell A de 56.0, la polea 2 tiene una dureza Rockwell C de 50.0, y de la polea C se desconoce la dureza, pero se sabe que tiene un esfuerzo último aproximado de 150,000 psi. ¿Cuál de las tres poleas debe seleccionarse? (4) La figura muestra la curva de fatiga de un acero. Este acero se utiliza para fabricar una barra que será sometida a esfuerzos cíclicos en tensión. Un ciclo de esfuerzos consiste en aplicar una fuerza en tensión sobre la barra y luego eliminar la fuerza. Cada ciclo de aplicación del esfuerzo dura dos minutos. 84 700 Esfuerzo (MPa) 600 500 400 300 200 100 0 1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 1.E+08 1.E+09 ciclos Si la barra tiene un diámetro de 5 centímetros, ¿Cuál es el valor de la fuerza en tensión aplicada en cada ciclo para que la barra dure 2,000 horas? (5) El componente estructural de un puente tiene una resistencia a la fluencia de 75,000 psi, y una tenacidad a la fractura en deformación plana de 5,000 psi(pulg)1/2. Para asegurarse que la parte no fallará, se diseña de modo que el máximo esfuerzo aplicado sea un tercio de la resistencia a la fluencia. Se utilizará una prueba no destructiva capaz de detectar cualquier grieta interna o superficial mayor de 0.009 pulgadas de longitud. Asumiendo que f = 1.4, ¿posee la prueba no destructiva la sensibilidad requerida? Explique. (6) Para un acero sometido a temperaturas elevadas, el tiempo de ruptura está dado por la siguiente ecuación: 117 ) tr = kσ 3.9 exp( 1.987 T donde k es una constante y T es la temperatura en grados Kelvin. Se sabe que para una temperatura de 980º C y un esfuerzo aplicado de 1,000 psi, el acero se rompe al cabo de 10,000 horas. Este acero se utilizará para fabricar una barra de área transversal circular que debe soportar una fuerza en tensión de 40,000 libras en un horno que se utiliza para la fabricación de ladrillos. La barra está localizada en un punto continuamente expuesto a una temperatura de 500º C. Diseñe la barra de forma que le permita operar por lo menos durante 10 años sin falla. 85 (7) En la figura se muestra el mecanismo de tracción de la rueda de un tren de vapor. Por medio de un pistón (el cual no se muestra en la figura) se aplica una fuerza "F" sobre la barra de sección circular. Esta fuerza se transmite hacia la rueda haciéndola girar. Suponga que usted trabaja en la fábrica de trenes como la persona encargada de diseñar la barra que debe hacer girar la rueda del tren. movimiento barra Fuerza aplicada "F" rueda Suponga que la fuerza aplicada sobre la barra siempre es axial. Para fabricar la barra, usted puede escoger entre los siguientes materiales: Material Acero Normalizado Acero Normalizado Acero Normalizado Acero Recocido Tenacidad a la fractura (MPa m1/2) 1020 50.0 1040 87.4 1080 66.0 4340 36.0 De la figura se observa que la fuerza aplicada hace que el esfuerzo sobre la barra sea en compresión. Asuma que las propiedades mecánicas definidas a partir de la prueba en tensión son válidas en compresión (es decir, las propiedades mecánicas de la tabla “Mechanical Properties of Carbon and Alloy Steels son aplicables para la barra). En la siguiente página se muestran las curvas de fatiga para los cuatro metales de la tabla anterior. 86 Esfuerzo aplicado (MPa) 600 500 400 Acero4340 300 Acero1040 200 Acero1020 100 01.00E+00 Acero1080 1.00E+01 1.00E+02 1.00E+03 1.00E+04 1.00E+05 1.00E+06 1.00E+07 1.00E+08 Número de Ciclos 87 Los criterios de diseño que usted debe considerar para fabricar la barra son los siguientes: a. El departamento de manufactura le informa que por limitaciones en el equipo que se usará para manufacturar la barra, el diámetro de diseño de ésta debe ser de 4 cm. b. La barra se fabricará por medio de un proceso de forja. El departamento de manufactura le informa que la ductilidad mínima que debe tener el material para poder ser forjado es de 30% en reducción de área. c. El departamento de tracción le informa que la máxima fuerza de diseño que el pistón le aplicará a la barra es de 550,000 N. d. El departamento de tracción también le informa que debido a la forma como opera el pistón de vapor, el material de la barra debe ser capaz de resistir golpes sin fracturarse. Ellos estiman que se requiere una Resistencia al Impacto Izod de 60 J o mayor para que el mecanismo funcione adecuadamente. e. El departamento de control de calidad le informa que el equipo de detección de grietas internas que ellos tienen disponible solamente puede detectar grietas de una longitud de 20 mm o mayores. f. El departamento de ruedas le informa que ellos usarán un material con una dureza de 56 HRA para fabricar las ruedas del tren. Ellos consideran que en caso de desgaste, es más fácil cambiar la barra que la rueda, por lo que sugieren que la barra tenga una dureza menor a 56 HRA. g. Finalmente, usted estima que cada vez que la rueda gire una vuelta completa la barra estará sometida a un ciclo de esfuerzo. Usted desea diseñar la barra de modo que dure 106 ciclos de esfuerzo antes de fallar por fatiga. Con toda esta información, seleccione el material que cumple con todos los requisitos de diseño de la barra. En caso de eliminar algún material por no cumplir uno o varios de los requisitos, justifique la razón de por qué no los cumple. Resuma su respuesta en la siguiente tabla: Material ¿Se puede Si no se puede usar, explique brevemente usar? por qué (sí/no) Acero 1020 Normalizado Acero 1040 Normalizado Acero 1080 Normalizado Acero 4340 Recocido 88 (8) Usted es el gerente de mantenimiento de una fábrica. Uno de los equipos bajo su responsabilidad consiste en una rueda que se mueve sobre un riel, tal como se muestra en la figura. Un día ocurre un accidente con el equipo y la rueda se rompe, y su responsabilidad es mandar a fabricar otra rueda para sustituir la dañada. Rueda Riel Usted va a un taller de maquinado, y le dicen que tienen tres aceros de los cuales puede fabricarse la rueda. Estos son: Material Acero 1 Acero 2 Acero 3 Dureza 72.3 HRA 170 HB (Standard Ball) 66.4 HRA Usted sabe que habrá desgaste entre la rueda y el riel. Por el tipo de equipo, decide que el desgaste se de en la rueda y no en el riel. Para seleccionar el material, mide la dureza del riel obteniendo un valor de 32.5 HRC. Con esta información seleccione el acero más adecuado para fabricar la rueda. 89 (9) Suponga que usted está contratado como Ingeniero en una fábrica que elabora piezas metálicas por medio de procesos que utilizan deformación plástica. Para elaborar estas piezas, se utiliza una prensa hidráulica especial, y su responsabilidad principal es garantizar que el proceso de fabricación no se detenga bajo ninguna circunstancia. Un día, usted llega a la fábrica, y encuentra que la prensa hidráulica está arruinada, siendo necesarias dos semanas completas para repararla. Como el proceso de fabricación no debe detenerse, su jefe inmediato superior le sugiere que construya una prensa utilizando un gato hidráulico (de los que se utilizan para cambiar las llantas de los carros) y una armazón de acero, tal como se ilustra: Barras de acero E=200 Gpa Discos metálicos Cuando se aplica presión sobre los discos, las barras de acero se deforman. Gato hidráulico El área sobre la cual se debe aplicar la presión, consiste en un disco metálico de 7.6 cm de diámetro, tal como se muestra: Diámetro = 7.6 cm La fuerza aplicada por el gato hidráulico (F) se distribuye sobre dos barras laterales, tal manera que sobre cada barra actúa una fuerza F/2. La deformación resultante cada barra se mide utilizando un dispositivo capaz de detectar deformaciones incrementos de 0.01 mm. En otras palabras, este dispositivo (llamado micrómetro) capaz de medir deformaciones de 0.01 mm, 0.02 mm, 0.03 mm, etc. de en en es 90 La deformación de cada barra se mide utilizando un dispositivo capaz de medir incrementos de deformación de 0.01 F F/2 F/2 La presión que el gato hidráulico debe ejercer sobre los discos metálicos debe ser de 1,500 psi (10.3 MPa). Recuerde que la presión es igual a la fuerza dividida entre el área (p = F/A). Suponga que las barras laterales se hacen de acero 1020 normalizado a. Calcule el diámetro inicial que deben tener las barras laterales, si la prensa está aplicando una presión de 1,500 psi sobre los discos, y se desea que el esfuerzo sobre cada una de las barras sea igual al 80% del esfuerzo de fluencia del material. b. Para el diámetro calculado en el numeral anterior, ¿Cuál será la deformación que se espera leer en el micrómetro mientras se aplica la presión de 1,500 psi? c. Para el diámetro previamente calculado, ¿Cuál es la máxima presión (en psi) que se puede aplicar sobre los discos metálicos sin que las barras laterales sufran deformación permanente? d. Para fabricar los discos metálicos, se utilizará acero 4340. Suponga que este material se obtiene en estado recocido. Se ha determinado que para evitar el desgaste excesivo durante la operación de la prensa, es necesario que los discos tengan una dureza mínima de 38 HRC. También se ha determinado que los discos no deben ser excesivamente frágiles, ya que cualquier golpe podría dañarlos. Para evitar excesiva fragilidad, se requiere que el porcentaje de reducción de área del material sea de 42% o mayor. Demuestre que el acero 4340 en estado recocido no puede utilizarse para fabricar los discos de la prensa. 91 (10) Una barra cilíndrica de acero tiene un diámetro inicial de 1.5 cm, y una longitud inicial de 25 cm. Se desea estirar la barra en tensión, de manera que se deforme hasta adquirir una longitud permanente final de 31.25 cm. El acero responde a la curva esfuerzo - deformación unitaria mostrada. a. Encuentre la magnitud de la fuerza que debe aplicarse sobre la barra para causarle la deformación permanente deseada. Deje constancia sobre la curva de cualquier procedimiento gráfico que sea requerido. b. Encuentre la longitud total que debe tener la barra mientras se aplica la fuerza, para lograr que su longitud (sin la fuerza aplicada) sea de 31.25 cm. Deje constancia sobre la curva de cualquier procedimiento gráfico que sea requerido. 25,000 Esfuerzo (kPa) 20,000 15,000 10,000 5,000 0 0 0.5 1 1.5 2 2.5 3 3.5 4 4.5 Deformación unitaria 92 (11) A continuación se muestran las propiedades mecánicas de tres tipos de aceros diferentes. Tipo acero de Esfuerzo último (MPa) 1020 1080 4140 394.7 615.4 655.0 Esfuerzo de fluencia (MPa) 294.8 375.8 417.1 % EL % Dureza Reducción HB de área 36.5 24.7 25.7 66.0 45.0 56.9 111 174 197 Resistenci a al impacto Izod (J) 123.4 6.1 54.5 a. Suponga que usted debe fabricar una pieza para una máquina, la cual estará sometida a fricción y fuerzas que originan desgaste sobre el material. ¿Cuál de los tres aceros sería el más adecuado para fabricar la pieza? Justifique. b. Suponga que a usted le piden fabricar unos clavos especiales para colocarlos en paredes de concreto. Los clavos serán introducidos a golpes con un martillo. ¿Cuál de los tres materiales sería el más adecuado para fabricar los clavos? Justifique. (12) En el laboratorio de materiales de la UCA, se mide la dureza de un metal desconocido A, y se encuentra un valor de 64.7 HRA. En el laboratorio de materiales del ITCA se mide la dureza de un metal diferente, pero también desconocido designado por B, y se obtiene 40 HRC. Se debe seleccionar uno de estos dos metales para fabricar unas piezas por medio de procesos de corte, es decir, procesos que requieren cortar al material utilizando herramientas con filo. ¿Cuál de los dos metales será el más fácil de cortar? Justifique. 93 (13) Un eje de acero de 20 cm de largo y 1.5 cm de diámetro se somete a una carga vibratoria que tiene una frecuencia de 500 vibraciones por minuto. La fuerza aplicada es de 166 N, y el esfuerzo en tensión es igual al esfuerzo en compresión sobre el eje. ¿Cuántas horas durará esta pieza antes de fallar por fatiga? Amplitud del esfuerzo (MPa) 200 150 100 50 0 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 1.E+08 1.E+09 1.E+10 1.E+11 Ciclos (14) Suponga que está en proyecto la construcción de un gaseoducto desde México hasta El Salvador. El gaseoducto no es más que una tubería de acero dentro de la cual se transportará gas natural a presión elevada. Suponga que este proyecto se hace realidad cuando usted se gradúa de la Universidad, y su primer trabajo lo obtiene con la compañía que fabricará el gaseoducto. La tubería donde se transportará el gas tiene un diámetro interno de 20 pulgadas, y un espesor de 0.25 pulgadas. Será fabricada con acero Ni-Cr, con las siguientes propiedades: Kic = 45,800 psi(pulg)1/2, σy = 238,000 psi. El gas dentro de la tubería está a una presión de 5,000 psi. La ecuación que relaciona al esfuerzo en la pared de la tubería con la presión interna se muestra a continuación: 94 σ = pD 2t Donde: σ = esfuerzo sobre las paredes de la tubería. D = diámetro interno de la tubería. t = espesor de las paredes de la tubería. p = presión en el interior de la tubería. a. Demuestre que la tubería no se deforma plásticamente debido a la presión del gas en su interior. b. Suponga que su jefe le encarga que usted gestione la compra en el extranjero de los tubos de acero que se utilizarán para fabricar el gaseoducto. Un proveedor le proporciona un excelente precio (esto significa que le vende los tubos muy baratos), pero le advierte que el control de calidad durante la fabricación no es muy estricto, y que por tanto los tubos poseen pequeños defectos con un tamaño máximo de 0.05 pulgadas de largo. Para esta tubería, f = 1. Por supuesto, el tubo no debe fallar cuando esté transportando el gas. ¿Se pueden utilizar estos tubos baratos para fabricar el gaseoducto? Justifique. c. Para el problema anterior, ¿Cuál debe ser el tamaño máximo de los defectos internos en el material de la tubería que garantizan que ésta no falla en operación? (15) Una barra cuadrada de 5 x 20 mm fabricada con una aleación de Hierro - Cromo Níquel debe operar a 1040ºC durante 10 años sin romperse. ¿Cuál es la fuerza máxima que se le puede aplicar a esta barra? Suponga que el material responde a la curva de termofluencia de la figura 6-25 a del libro de texto (página 159) 95 (16) Metal A 700 Esfuerzo (psi) 600 500 400 300 200 100 0 1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 1.E+08 1.E+09 ciclos Metal B 700 Esfuerzo (psi) 600 500 400 300 200 100 0 1.E+00 1.E+01 1.E+02 1.E+03 1.E+04 1.E+05 1.E+06 1.E+07 1.E+08 1.E+09 ciclos En las figuras anteriores se muestran las curvas de fatiga de dos metales diferentes. Con uno de estos materiales se construirá el eje de un motor. El esfuerzo máximo sobre este eje está dado por la ecuación 96 10.18 l F d3 Recuerde que “l” es la longitud de la barra en pulgadas, “F” es la fuerza aplicada en libras, “d” es el diámetro del eje en pulgadas, y σ es el esfuerzo en psi. Se desea que el eje dure 106 ciclos de aplicación de la fuerza. La fuerza aplicada sobre el eje es de 25 lbs y su longitud es de 2 pulgadas. Con esta información, seleccione el metal que debe utilizarse para que el eje tenga el menor diámetro posible. Justifique su selección. σ= (17) A continuación se muestra una tabla con algunas propiedades mecánicas de ciertos aceros. Todos estos datos, a excepción del coeficiente de endurecimiento por deformación, han sido tomados del "Metals Handbook, desk edition". Material Acero 1020 Acero 1040 Acero 1080 Acero 4130 Acero 4340 Esfuer zo último (MPa) 448.2 Esfuerzo de fluencia (Mpa) 330.9 % % Durez Resisten n Elongació Reducción a (HB) cia al n de área impacto Izod (J) 36.0 59.0 143 86.8 0.12 620.5 413.7 25.0 50.0 201 48.8 0.20 965.3 586.1 12.0 17.0 293 6.8 0.15 668.8 436.4 25.5 59.5 197 86.4 0.35 1279.0 861.8 12.2 36.3 363 15.9 0.25 Suponga que usted trabaja en un ingenio azucarero, y le piden seleccionar el acero más adecuado para construir un par de engranes, tal como los que se muestran en la siguiente figura: En las preguntas que siguen a continuación, escriba el nombre del acero que usted usaría para construir los engranes. Cada una de las condiciones que se describen en las diferentes preguntas son independientes entre sí. (Es decir, una pregunta no está relacionada con ninguna de las otras). 97 • Si los engranes estarán sometidos a golpes (fuerzas de impacto) ¿Cuál de todos los materiales es el mejor para su construcción? • Entre más pequeños sean los engranes, mayores serán los esfuerzos aplicados sobre ellos, y que deben soportar en funcionamiento. Entre más grandes sean los engranes, menores serán los esfuerzos aplicados sobre ellos, y que deben soportar en funcionamiento (Siempre y cuando la fuerza que transmitan se mantenga constante). Si los engranes siempre deben trabajar en la zona elástica de la curva esfuerzo - deformación unitaria, ¿Cuál de todos los materiales mostrados en la tabla debe utilizarse para que los engranes fabricados sean lo más pequeños posible? • Si los engranes estarán sometidos a fricción y rozamiento, los cuales pueden causar un desgaste significativo sobre su superficie, ¿Cuál de todos los metales que se muestran en la tabla es el más adecuado para fabricar los engranes y resistir el desgaste? • Si para fabricar los engranes se escoge el acero 1080, y el material se somete a una prueba de dureza Rockwell en las escalas A y C, ¿Qué valores de dureza se obtendrían en estas escalas? Asuma que los valores de dureza Brinell que se muestran en la tabla corresponden a un penetrador de bola estándard. (18) Suponga que el acero 1020 "as-rolled" usado para fabricar el tanque esférico tiene una tenacidad a la fractura en deformación plana de 20 MPa*m1/2. Para todos los cálculos asuma que f=1. Este material será sometido a una prueba de rayos X para determinar el tamaño de los defectos internos que posea. En caso de existir un aumento no deseado de la presión del gas, se desea que el tanque esté diseñado de modo que falle por deformación plástica antes de que falle por fractura. En otras palabras, si la presión aumentara demasiado, se desea que el tanque tenga la capacidad de deformarse plásticamente antes de que se fracture por crecimiento de grietas. Por esta razón, como criterio de diseño se decide que los defectos internos del material comiencen a crecer cuando el esfuerzo aplicado sobre las paredes se iguale a la resistencia a la tensión del material. Como dueño del negocio de fabricación de tanques, usted es el encargado de comprar el acero para construirlo. ¿Cuál es el tamaño máximo de la grieta interna que usted aceptaría que tenga el material para poder satisfacer las condiciones de diseño del tanque? Si para fabricar el tanque usted puede escoger entre el metal con Kic=20 MPa*m1/2 (al que llamaremos metal A) y otro metal con Kic= 37.4 MPa*m1/2(al que llamaremos metal B), ¿Cuál de estos dos metales le permitiría tener la grieta más grande sin que el tanque se fracture antes de llegar a la estricción? Justifique. 98