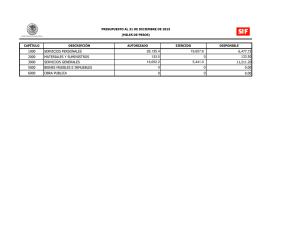
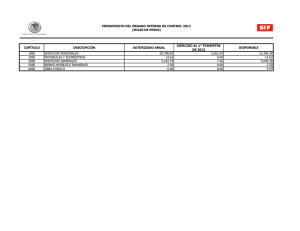
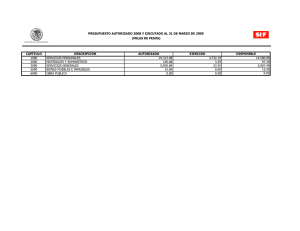
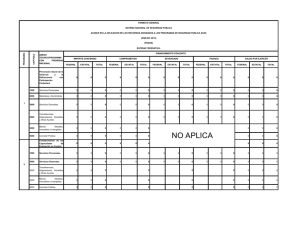
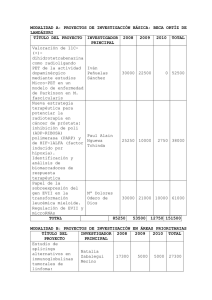
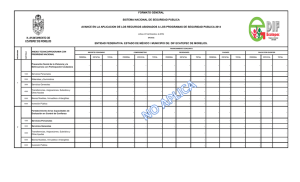
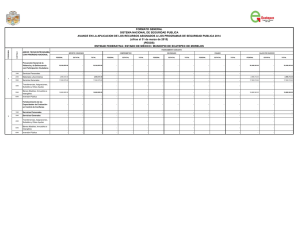
C(x) = 1000 + ½ (x/50) Ingreso: I(x) = 2x Utilidad: U(x) = 2x – 1000
Anuncio

Facultad de Contabilidad y Finanzas 2008 – I SOLUCIONARIO DE LA PRÁCTICA CALIFICADA Nº 2 - A Curso Profesor Ciclo : : : ANÁLISIS MATEMÁTICO II Ing. Oscar Reyes Almora VI 1. Precio: $2 por unidad. Función de costo C por producir x unidades es (en dólares): C(x) = 1000 + ½ (x/50)2 a. Escriba la expresión para la utilidad total U como una función de x. Ingreso: I(x) = 2x Utilidad: U(x) = 2x – 1000 – x2/5000 b. Determine el valor de x que maximiza la utilidad U. (1,0 punto) (1,0 punto) U´(x) = 2 – x/2500 = 0 → x = 5000 c. ¿Cuál es el valor de la utilidad máxima? (1,0 punto) U(5000) = 2(5000) – 1000 – (5000)2/5000 = 4000 dólares d. ¿Cuál sería la utilidad si se produjeran 6000 unidades? (1,0 punto) 2 U(6000) = 2(6000) – 1000 – (6000) /5000 = 3800 dólares 2. Ecuación de demanda: p = 8 – 0,02x, Función de costo C = 200 + 2x, encuentre el x que maximiza el ingreso y la utilidad. Calcule la utilidad máxima. (3,0 puntos) I(x) = (8 – 0,02x)x = 8x – 0,02 x2 Ingreso: Valor que maximiza el Ingreso: Utilidad: I´(x) = 8 – 0,04x = 0 → x = 200 U(x) = 8x – 0,02 x2 – 200 – 2x = – 0,02 x2 – 200 + 6x Valor que maximiza la Utilidad: U´(x) = – 0,04 x + 6 = 0 → x = 150 U(150) = – 0,02 (150)2 – 200 + 6(150) = 250 u.m. Utilidad Máxima: 3. Determine los extremos absolutos de las funciones siguientes: 3 2 a. f(x) = x – 18x + 60x en -1 ≤ x ≤ 5 (2,5 puntos) f ´(x) = 3x2 – 36x + 60 = 3(x2 – 12x + 20) Extremos locales: 3(x – 2) (x – 10) = 0 → x = 2 ó x = 10 ∉ [-1, 5] f ´´(x) = 6x – 36 → f ´´(2) = 6(2) – 36 = -24 < 0 → f ´´(10) = 6(10) – 36 = 26 > 0 → máximo local → mínimo local f(-1) = (-1)3 – 18(-1)2 + 60(-1) = -1 – 18 – 60 = - 79 f(2) = (2)3 – 18(2)2 + 60(2) = 56 f(5) = (5)3 – 18(5)2 + 60(5) = 125 – 450 + 300 = - 25 ∴ en x = -1 se presenta un mínimo absoluto y en x = 2 un máximo absoluto 2 b. g(x) = (x + 1)(x – 6)/x en ½ ≤x≤2 (2,5 puntos) g(x) = (x – 5x – 6 )/x → g ´(x) = [(2x – 5)x – 2x(x – 5x – 6 )]/ x 2 2 2 2 4 g ´(x) = [2x3 – 5x2 – 2x3 + 10x2 + 12x )]/ x4 → g ´(x) = (5x2 + 12x )/ x4 Extremos locales x = -12/5 = - 2,4∉ [ ½ , 2] g(½) = ((½)2 – 5(½) – 6 )/ (½)2 = ( ¼ – 5/2 – 6) / 1/4 = - 33 g(2) = ((2)2 – 5(2) – 6 )/ (2)2 = - 3 ∴ en x = ½ se presenta un mínimo absoluto y en x = 2 un máximo absoluto 4. Método de Newton, calcule aproximadamente (con cinco cifras decimales) la mayor de 3 2 las raíces reales de F(x) = – x + 4x – 3 , cuya gráfica es: (4,0 puntos) F´(x) = – 3x2 + 8x x1 = 4,00000 x2 = 3,81250 x3 = 3,79154 x4 = 3,79129 x5 = 3,79129 5. Empleando el Método de Newton, determine el valor aproximado de x (en milésimas), 3 para el cual se presenta un mínimo local en la función h(x) = (x – 15x)/3. (4,0 puntos) h(x) = x3/3 – 5x → h´(x) = x2 – 5 → h´´(x) = 2x Cálculo de las raíces: h(x) = x(x2/3 – 5) = 0 Región ]-∞, -√15 [ ] -√15, 0 [ ]0, √15 [ ]√15, ∞ [ x1 = 2,000 x2 = 2,250 x -4 -1 1 4 → x = 0, x = -√15, x = √15 h(x) -1,3333 4,6666 -4,6666 1,3333 x3 = 2,236 Ubicación Debajo Sobre Debajo Sobre x4 = 2,236 EL PROFESOR Facultad de Contabilidad y Finanzas 2008 – I SOLUCIONARIO DE LA PRÁCTICA CALIFICADA Nº 2 - B Curso Profesor Ciclo : : : ANÁLISIS MATEMÁTICO II Ing. Oscar Reyes Almora VI 1. Precio: $2 por unidad. Función de costo C por producir x unidades es (en dólares): C(x) = 1000 + ½ (x/50)2 a. Escriba la expresión para la utilidad total U como una función de x. Ingreso: I(x) = 2x Utilidad: U(x) = 2x – 1000 – x2/5000 b. Determine el valor de x que maximiza la utilidad U. (1,0 punto) (1,0 punto) U´(x) = 2 – x/2500 = 0 → x = 5000 c. ¿Cuál es el valor de la utilidad máxima? (1,0 punto) 2 U(5000) = 2(5000) – 1000 – (5000) /5000 = 4000 dólares d. ¿Cuál sería la utilidad si se produjeran 6000 unidades? (1,0 punto) U(6000) = 2(6000) – 1000 – (6000)2/5000 = 3800 dólares 2. Ecuación de demanda: p = 1000 – x. Función de costo C = 3000 + 20x, encuentre el valor de x que maximiza el ingreso y la utilidad. Halle la utilidad máxima. (3,0 puntos) I(x) = (1000 – x)x = 1000x – x2 Ingreso: Valor que maximiza el Ingreso: I´(x) = 1000 – 2x = 0 → x = 500 U(x) = 1000x – x2 – 3000 – 20x = – x2 – 3000 + 980x Utilidad: Valor que maximiza la Utilidad: U´(x) = – 2 x + 980 = 0 → x = 490 U(490) = – (490)2 – 3000 + 980(490) = 237100 u.m. Utilidad Máxima: 3. Determine los extremos absolutos de las funciones siguientes: en -3 ≤ x ≤ 3/2 3 a. f(x) = x – 3x + 2 2 (2,5 puntos) 2 f ´(x) = 3x – 3 = 3(x – 1) Extremos locales: 3(x + 1) (x – 1) = 0 → x = -1 ó x = 1 f ´´(x) = 6x → f ´´(-1) = 6(-1) = - 6 < 0 → f ´´(1) = 6(1) = 6 > 0 → máximo local → mínimo local 3 f(-3) = (-3) – 3(-3) + 2 = -27 + 9 + 2 = - 16 f(-1) = (-1)3 – 3(-1) + 2 = -1 + 3 + 2 = 4 f(1) = (1)3 – 3(1) + 2 = 1 – 3 + 2 = 0 f(3/2) = (3/2)3 – 3(3/2) + 2 = 27/8 – 9/2 + 2 = 7/8 ∴ en x = -3 se presenta un mínimo absoluto y en x = -1 un máximo absoluto 2 b. g(x) = (x – 1)(x – 3)/x en ½ ≤x≤2 (2,5 puntos) g(x) = (x2 – 4x + 3 )/x2 → g ´(x) = [(2x – 4)x2 – 2x(x2 – 4x + 3 )]/ x4 g ´(x) = [2x3 – 4x2 – 2x3 + 8x2 – 6x )]/ x4 → g ´(x) = (4x2 – 6x )/ x4 Extremo local x = 6/4 = 1,5 g(½) = ((½)2 – 4(½) + 3 )/ (½)2 = ( ¼ – 2 + 3) / 1/4 = 5 g(1,5) = ((1,5)2 – 4(1,5) + 3)/ (1,5)2= - 0,3333… g(2) = ((2)2 – 4(2) + 3 )/ (2)2= - ¼ = - 0,25 ∴ en x = 1,5 se presenta un mínimo absoluto y en x = ½ un máximo absoluto 4. Método de Newton, calcule aproximadamente (con cinco cifras decimales) la mayor de 3 2 las raíces reales de F(x) = x + 4x – 4, cuya gráfica es: (4,0 puntos) F´(x) = 3x2 + 8x x1 = 1,00000 x2 = 0,90909 x3 = 0,90324 x4 = 0,90321 x5 = 0,90321 5. Empleando el Método de Newton, determine el valor aproximado de x (en milésimas), 3 para el cual se presenta un mínimo local en la función h(x) = (x – 15x)/3. (4,0 puntos) h(x) = x3/3 – 5x → h´(x) = x2 – 5 → h´´(x) = 2x Cálculo de las raíces: h(x) = x(x2/3 – 5) = 0 Región ]-∞, -√15 [ ] -√15, 0 [ ]0, √15 [ ]√15, ∞ [ x1 = 2,000 x2 = 2,250 x -4 -1 1 4 → x = 0, x = -√15, x = √15 h(x) -1,3333 4,6666 -4,6666 1,3333 x3 = 2,236 Ubicación Debajo Sobre Debajo Sobre x4 = 2,236 EL PROFESOR