Corrientes en la capa superior del océano

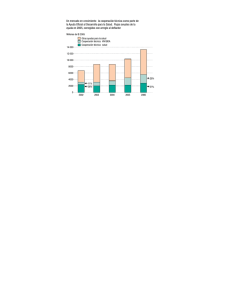
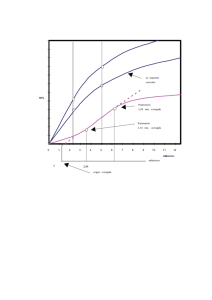
Corrientes en la capa superior del océano
Corrientes superficiales en los océanos Atlántico
(arriba) e Indico (derecha). Adaptados de Tomczak
(Regional Oceanography, an Introduction, ver:
www.es.flinders.edu.au/~mattom/regoc/index.html).
Los giros subtropicales (anticiclónicos) en cada
caso están sombreados de rosa. El área subpolar del
HS (en verde) representa a la Corriente Circumpolar
Antártica y las masas de agua al sur de la misma.
El giro ciclónico del Mar de Weddell está
representado en violeta.
La circulación en el Indico tropical (beige) se
invierte en respuesta a los cambios estacionales del
patrón del viento. El panel superior derecho
representa la circulación del Monzón del Noreste
(entre marzo y abril) y el panel inferior derecho el
Monzón del Sudoeste (entre septiembre y octubre).
Circulación superficial del Pacífico. Ver epígrafe de las figuras anteriores.
El modelo de Sverdrup (1947)
Presión: 1 / ρ (∂p / ∂x)
Coriolis: f v
Fricción: AV ∂2u / ∂z2
β My = rotZ τ0
z = (6000*3.1415*(-.1)/(4000*1.6e-11*1026))*sin(3.1415*y/4000)*(1-(x/6000))/1000000
4000
τ
= a Π 0 sen Π y (1-x/a)
b β ρ0
b
3500
b= 4000 km
3000
τ = − τ 0 cos Π y
b
y (km )
2500
2000
1500
1000
500
0
0. 08
0.0 4
0
-0.0 4
-0 .0 8
0
500
1000
1500
2000
2500
3000
x (km)
3500
4000
4500
5000
5500
6000
a= 6000 km
Líneas de corriente para el transporte de masa (103 Kg/s) en el Pacífico ecuatorial
este, calculadas a partir de la relación de Sverdrup (adaptado de Reid, 1948).
Transporte de Sverdrup aplicado globalmente usando los vientos de Hellerman y
Rosenstein (1983). El intervalo entre contornos es 10 Sverdrups (1 Sv = 106 m3/s ≈
109 Kg/s, adaptada de Tomczak y Godfrey,1994).
Latitud
Latitud
Corriente Nor-Ecuatorial
Contra-corriente
Nor-Ecuatorial
Sur
Norte
Oeste
Este
Corriente SurEcuatorial
Transporte de masa meridional (My, izquierda) y zonal (Mx, derecha) en el
Pacífico ecuatorial este, calculados empleando la relación derivada por Sverdrup
(líneas) y datos a partir de hidrográficos (temperatura y salinidad) y el cálculo
geostrófico (puntos). Los transportes están dados en 103 Kg/s a través de un área
vertical de 1000 m de profundidad y 1 m de ancho. Aproximadamente son
equivalentes a 0.1 Sv por grado de latitud. Notar las escalas diferentes para Mx
y My (adptado de Reid, 1948).
Bomba de Ekman (pumping)
Tensión del viento en la superficie del mar (τ0 en Pa). Cada contorno
representa una magnitud de 0.05 Pa.
La teoría de Ekman muestra que el transporte de Ekman es
MEk = τ0 / f
La ecuación de continuidad es:
∇h • Vh + ∂w / ∂z = 0
tomando w = 0 en la superficie ∂w / ∂z = wEk / DE
WEk = 1 / ρ ∇h • MEk
WEk = 1 / ρ (∂τy / ∂x + ∂τx / ∂y) = 1 / ρ ∇ × (τ0 / f)
Velocidad vertical (m/año) a través de la base de la capa de Ekman
calculada a partir de la tensión del viento en superficie.
Intensificación de las corrientes en el
borde oeste (Stommel, 1948)
Presión: 1 / ρ (∂p / ∂x)
Coriolis: f v
Fricción vert: AH ∂2u / ∂z2
Fricción horiz: -R*u, -R*v
Mx = ∂ψ / ∂y
My = - ∂ ψ / ∂x
R (∂2ψ / ∂x2 + ∂2 ψ / ∂y2) + β ∂ψ / ∂x = ∂ / ∂y (τ0x / ρ 0)
= a Π τ0 sen Π y (e(-xβ/R) - x/a -1)
b β ρ0
b
Solución de Stommel tierra no rotante
Solución de Stommel tierra rotante “plano β”
4000
b= 4000 km
z = 6 000*3.141 5*(-.1)/ (4000 *1.6e -11*1026 )*sin(3.1415 *y/400 0)*(exp(-(x/60 00)/.0 25)+(x/600 0)-1)/10000 00
4 000
ε = R / a β = 0 .025
3500
b= 4000 km
3 500
3000
3 000
τ = − τ 0 cos Π y
b
2500
2 500
2 000
2000
1 500
1500
1 000
1000
500
500
0.08
0.0 4
= a Π τ0 se n Π y (e (-xβ/R) - x /a -1 )
b β ρ0
0
0
-0.0 4
0
-0 .08
500
100 0
150 0
200 0
25 00
3 000
3 500
4000
b
4500
5000
5500
600 0
a= 6000 km
0
0
500
1000
1500
2000
2500
3000
3500
4000
4500
5000
5500
6000
a= 6000 km
Líneas de corriente del transporte (en Sverdrups) para una solución plano β y para el perfil de tensión del viento
indicado en la figura de la izquierda. La intensidad máxima de oestes y alisios es 0.1 Pa. En el “interior” el flujo se
encuentra en balance de Sverdrup, pero al aproximarse al borde W, donde la velocidad crece, la fricción es relevante.
Solución de Munk fricción turbulenta
AH ∂2v / ∂y2
AH ∂2v / ∂x2
Detalle de la recirculación
próxima al borde oeste. La
misma sólo es evidente al
imponer fricción horizontal
turbulenta de tipo newtoniana,
que permite, además que la
velocidad tangencial también
sea nula en los bordes.
El océano real
Imagen de temperatura superficial
del mar en el Atlántico SW un día de
diciembre de 1986. Nótese que las
aguas cálidas asociadas a la C.
Brasil se extienden hacia el sur
cerca del borde oeste, formando la
llamada “extensión de la C. Brasil”,
el eddy cálido al sur del núcleo
principal de la corriente
probablemente se ha desprendido
de la misma hace pocos días. El
flujo meridioal al E de la C. Brasil se
invierte (hacia el N), creando una
recirculación semejante a la que
resulta de la solución de Munk.