30.84. Un largo conductor cilíndrico de radio a tiene dos cavidades
Anuncio

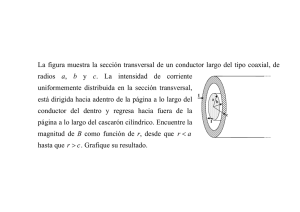
30.84. Un largo conductor cilíndrico de radio a tiene dos cavidades cilíndricas de diámetro a lo largo de toda su longitud, como se muestra en la figura. Una corriente, I, se dirige hacia fuera de la pagina y es uniforme por toda la sección transversal del conductor. Encuentre la magnitud y dirección del campo magnético en el punto P1 en función de µo, I, r y a. El área de la sección transversal del conductor es la siguiente: A = π[a^2 - (a^2/4) - (a^2/4)] = (π*a^2)/2 La densidad de corriente por unidad de área es: J = I/A = 2*I/(π*a^2) Para sacar el campo magnético se toma primero como si el conductor fuera sólido y después se le resta el campo que producirían los cilindros huecos como si fueran conductores a partir de la densidad de corriente por unidad de área. Para el cilindro grande(radio a) la corriente sería: I (sólido) = Area*J = J*π*a^2 Para los cilindros huecos (radio a/2) la corriente es: I (hueco)= Area*J = J*π*(a/2)^2 Por ley de Ampére el campo en el punto P1 es: B= ((µo*J* π*a^2)/2* π*r) – ((µo * J* π*(a/2)^2)/2* π*(r-a/2)) – ((µo* J* π*(a/2)^2)/2* π*(r+a/2)) =(µo*J*a^2)*(2*r^2 - a^2)/(2*r)*(4*r^2 – a^2) =(µo*I)*(2*r^2 - a^2) / (π*r)*(4*r^2 – a^2) Hacia la izquierda