Ejercicios de Modelos Econométricos
Anuncio
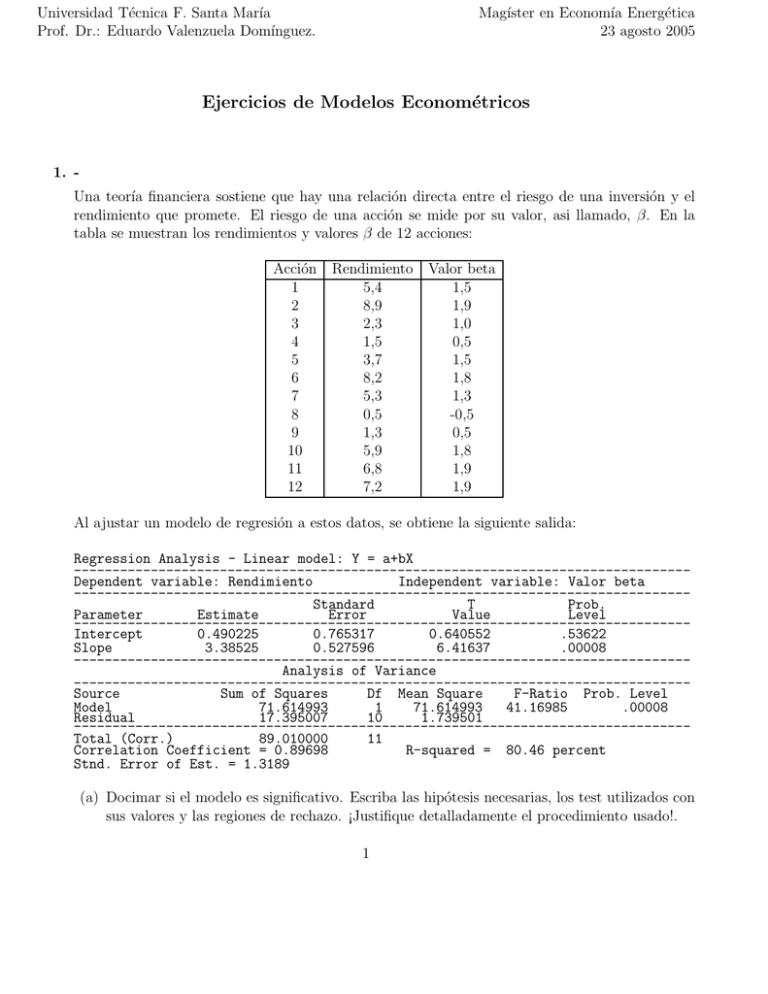
Universidad Técnica F. Santa Marı́a Prof. Dr.: Eduardo Valenzuela Domı́nguez. Magı́ster en Economı́a Energética 23 agosto 2005 Ejercicios de Modelos Econométricos 1. Una teorı́a financiera sostiene que hay una relación directa entre el riesgo de una inversión y el rendimiento que promete. El riesgo de una acción se mide por su valor, asi llamado, β. En la tabla se muestran los rendimientos y valores β de 12 acciones: Acción 1 2 3 4 5 6 7 8 9 10 11 12 Rendimiento 5,4 8,9 2,3 1,5 3,7 8,2 5,3 0,5 1,3 5,9 6,8 7,2 Valor beta 1,5 1,9 1,0 0,5 1,5 1,8 1,3 -0,5 0,5 1,8 1,9 1,9 Al ajustar un modelo de regresión a estos datos, se obtiene la siguiente salida: Regression Analysis - Linear model: Y = a+bX -------------------------------------------------------------------------------Dependent variable: Rendimiento Independent variable: Valor beta -------------------------------------------------------------------------------Standard T Prob. Parameter Estimate Error Value Level -------------------------------------------------------------------------------Intercept 0.490225 0.765317 0.640552 .53622 Slope 3.38525 0.527596 6.41637 .00008 -------------------------------------------------------------------------------Analysis of Variance -------------------------------------------------------------------------------Source Sum of Squares Df Mean Square F-Ratio Prob. Level Model 71.614993 1 71.614993 41.16985 .00008 Residual 17.395007 10 1.739501 -------------------------------------------------------------------------------Total (Corr.) 89.010000 11 Correlation Coefficient = 0.89698 R-squared = 80.46 percent Stnd. Error of Est. = 1.3189 (a) Docimar si el modelo es significativo. Escriba las hipótesis necesarias, los test utilizados con sus valores y las regiones de rechazo. ¡Justifique detalladamente el procedimiento usado!. 1 (b) Interprete la tabla de análisis de varianza. (c) ¿Qué revela el modelo de regresión sobre la relación planteada en tal teorı́a?. (d) Se desea probar la hipotesis que estipula que el rendimiento medio de las acciónes, para un valor β de 0,8 es de 4,5 versus que es mayor. 2 2. Se estimó un modelo de regresión múltiple a partir de 25 observaciones, obteniendose los siguientes resultados: Coeficiente β0 β1 β2 β3 β4 Estimación 10,6 28,4 4,0 12,7 0,84 Error estandar 2,1 11,2 1,5 14,1 0,76 (a) Verificar si es posible rechazar la hipotesis nula H0 : β1 = 0 al 95% de confianza. (b) En el modelo propuesto: Y = β0 + β1 X1 + β2 X2 + β3 X3 + β4 X4 + U ¿Que regresores son estadisticamente significativos?. (c) Usando los resultados de (b) prediga el valor de la respuesta para x∗ = (1, 1, 1, 1)t. 3 (1) 3. Se desea encontrar un modelo que represente al tiempo de CPU que se emplea en realizar un experimento de simulación. Para esto se registraron los resultados correspondientes a varias simulaciones en las cuales se observaron las siguientes variables: Y : Tiempo de CPU de la simulación X1 : Numero de corridas de la simulación X2 : Numero de instrucciones del programa X3 : Cuadrado de X2 Al ajustar secuencialmente los modelos con X1 , X2 y X3 , se obtuvo: 4 Model fitting results for: SIMULAR.tiempocpu -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 122.708059 18.960776 6.4717 0.0000 SIMULARC.corridas 0.510848 0.043571 11.7246 0.0000 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9130 SE= 37.903668 MAE= 29.894220 DurbWat= 2.197 Previously: 0.0000 0.000000 0.000000 0.000 14 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Analysis of Variance for the Full Regression -------------------------------------------------------------------------------Source Sum of Squares DF Mean Square F-Ratio P-value -------------------------------------------------------------------------------Model 197495. 1 197495. 137.466 .0000 Error 17240.3 12 1436.69 -------------------------------------------------------------------------------Total (Corr.) 214735. 13 R-squared = 0.919714 Stnd. error of est. = 37.9037 R-squared (Adj. for d.f.) = 0.913023 Durbin-Watson statistic = 2.19719 5 Model fitting results for: SIMULAR.tiempocpu -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 20.560513 3.834962 5.3613 0.0002 SIMULARC.corridas 0.597171 0.005477 109.0351 0.0000 SIMULARC.instruc 0.20203 0.00639 31.6167 0.0000 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9990 SE= 4.130272 MAE= 3.061539 DurbWat= 2.030 Previously: 0.9130 37.903668 29.894220 2.197 14 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Analysis of Variance for the Full Regression -------------------------------------------------------------------------------Source Sum of Squares DF Mean Square F-Ratio P-value -------------------------------------------------------------------------------Model 214548. 2 107274. 6288.35 .0000 Error 187.651 11 17.0591 -------------------------------------------------------------------------------Total (Corr.) 214735. 13 R-squared = 0.999126 Stnd. error of est. = 4.13027 R-squared (Adj. for d.f.) = 0.998967 Durbin-Watson statistic = 2.03047 6 Model fitting results for: SIMULAR.tiempocpu -------------------------------------------------------------------------------Independent variable coefficient std. error t-value sig.level -------------------------------------------------------------------------------CONSTANT 7.027844 3.071475 2.2881 0.0452 SIMULARC.corridas 0.594722 0.002818 211.0213 0.0000 SIMULARC.instruc 0.32346 0.021538 15.0184 0.0000 SIMULARC.instrucdos -0.000173 0.00003 -5.7033 0.0002 -------------------------------------------------------------------------------R-SQ. (ADJ.) = 0.9997 SE= 2.100567 MAE= 1.252286 DurbWat= 3.108 Previously: 0.9990 4.130272 3.061539 2.030 14 observations fitted, forecast(s) computed for 0 missing val. of dep. var. Analysis of Variance for the Full Regression -------------------------------------------------------------------------------Source Sum of Squares DF Mean Square F-Ratio P-value -------------------------------------------------------------------------------Model 214691. 3 71563.7 16218.8 .0000 Error 44.1238 10 4.41238 -------------------------------------------------------------------------------Total (Corr.) 214735. 13 R-squared = 0.999795 Stnd. error of est. = 2.10057 R-squared (Adj. for d.f.) = 0.999733 Durbin-Watson statistic = 3.10791 (a) Determine sobre la base de test apropiados, si se justifica la incorporación al modelo de las variables X2 o X2 y X3 . (b) Encuentre los coeficientes de correlación parcial de Y con X3 , dado X1 y dado X1 y X2 . 7 4. Se estimó un modelo de regresion multiple a partir de 25 observaciones, obteniendose los siguientes resultados: Coeficiente β0 β1 β2 β3 β4 Estimación 10,6 28,4 4,0 12,7 0,84 Error estandar 2,1 11,2 1,5 14,1 0,76 (a) Verificar si es posible rechazar la hipotesis nula H0 : β1 = 0 al 95% de confianza. (b) En el modelo propuesto: Y = β0 + β1 X1 + β2 X2 + β3 X3 + β4 X4 + U ¿Que regresores son estadisticamente significativos?. (c) Usando los resultados de (b) prediga el valor de la respuesta para x∗ = (1, 1, 1, 1)t. 8 (2) 5. En un estudio de determinación de la produccion final a costo de factores en el Reino Unido, se obtuvieron los siguientes resultados con base en informacion anual durante el periodo 1951 - 1969: PˆFt = 2, 033+ 0, 273Wt− 0, 521Xt+ 0, 256Mt + 0, 028Mt−1 + 0, 121P Ft−1 (0, 992) (0, 127) (0, 099) (0, 024) (0, 039) (0, 119) (3) Ademas se sabe que: R2 = 0, 984 y d = 2, 54. Aqui se tiene: P F : precios de la produccion final a costo de factores, W : salarios por empleado, X: producto interno bruto por persona empleada, M: precios de importacion, Mt−1 : precios de importacion rezagados 1 año y P Ft−1 : precios de la produccion final a costo de factores en el año anterior. (a) Analizar la validez del modelo. (b) Determinar si existe correlación serial y en caso de existir indique como corregirla. 9 6. Sobre la base de datos mensuales durante el periodo enero 1978 a diciembre 1987 , se obtuvieron los siguientes resultados de regresion: Ŷt = 0.00681 + 0.7581Xt Sβ = (0.02596)(0.27009) R2 = 0.4406 Ŷt = Sβ = R2 = 0.76214Xt (0.265799) 0.43684 donde: Y = tasa mensual de retorno sobre las acciones comunes de Texaco, en %. X = tasa mensual de retorno del mercado, en %. (a) Dados los resultados anteriores, ¿se conservarı́a el término constante en el primer modelo?. ¡Justifique!. (b) ¿Como se interpretan los coeficientes de pendiente en ambos modelos?. (c) ¿Pueden compararse los coeficientes R2 en los dos modelos?. ¡Justifique!. 10 7. La siguiente tabla muestra la captura de anchoas peruanas (captura, en millones de toneladas métricas) y el precio de la harina de pescado (precio, en dólares por tonelada) para los años 1975 a 1988: Año precio captura 75 76 77 78 79 80 81 82 83 84 85 86 87 88 190 160 134 129 172 197 167 239 542 372 245 376 454 410 7,23 8,53 9,82 10,26 8,96 12,27 10,28 4,45 1,78 4,0 3,3 4,3 0,8 0,5 Al ajustar un modelo de regresión a estos datos, se obtiene la siguiente salida: Regression Analysis - Linear model: Y = a+bX -------------------------------------------------------------------------------Dependent variable: precio Independent variable: captura -------------------------------------------------------------------------------Standard T Prob. Parameter Estimate Error Value Level -------------------------------------------------------------------------------Intercept 452.119 36.8235 12.278 .00000 Slope -29.4018 5.09084 -5.77544 .00009 -------------------------------------------------------------------------------Analysis of Variance -------------------------------------------------------------------------------Source Sum of Squares Df Mean Square F-Ratio Prob. Level Model 171413.89 1 171413.89 33.4 .00009 Residual 61667.610 12 5138.967 -------------------------------------------------------------------------------Total (Corr.) 233081.50 13 Correlation Coefficient = -0.857569 R-squared = 73.54 percent Stnd. Error of Est. = 71.6866 (a) Analice si el modelo es significativo, estipulando claramente las hipótesis necesarias, los estadigrafos utilizados con sus valores y las regiones de rechazo. ¡Justifique detalladamente el procedimiento usado!. (b) Interprete las sumas de cuadrados y la razón F y docime la bondad de ajuste del modelo. (c) ¿Qué permite concluir el modelo de regresión sobre la fenomeno analizado?. (d) Se desea probar la hipotesis que estipula que la varianza residual es de 5500. 11








