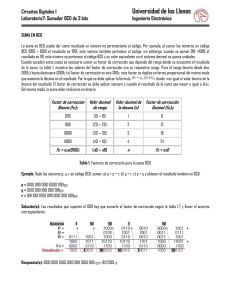
Aritmética de números en BCD

Aritmética de números
en BCD
M. en C. Erika Vilches
www.erika-vilches.com/teaching
erika@erika-vilches.com
El código 8421
• Es un tipo de código BCD (Binary coded
decimal)
• “Decimal Codificado a Binario” significa que
cada dígito decimal (0 al 9) es representado
por un código binario de 4 bits.
• La designación 8421 indica los pesos binarios
de los 4 bits (2^3, 2^2, 2^1, 2^0).
• Ventaja → Facilidad de conversión entre
8421 y decimal
Conversión Decimal / BCD
1
2
3
4
5
6
7
8
9
Dígito Decimal 0
0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
BCD
Códigos Inválidos
Con 4 bits es posible representar 16 números
(0000 al 1111), sin embargo en 8421 solo se
utilizan 10.
Los 6 códigos no utilizados - 1010, 1011, 1100,
1101, 1110 y 1111 - son inválidos en BCD 8421.
Conversión a BCD
Para expresar cualquier decimal en BCD,
simplemente reemplace cada dígito decimal
con el código de 4 bits correspondiente.
Ejercicio: Convertir el número decimal 9673 a BCD
Conversión a Decimal
• Iniciar con el bit del extremo derecho y
partir en grupos de 4 bits. Escribir el dígito
decimal representado por cada grupo de 4
bits.
Ejercicio: Convertir el código BCD
10000010001001110110 a decimal.
Suma BCD
1. Realizar la suma binaria normalmente.
2. Si la suma de los 4 bits es menor o igual a 9,
es un número BCD válido.
3. Si la suma de los 4 bits es mayor a 9 o si se
genera un carry fuera del grupo de los 4 bits,
es un resultado inválido. Añadir 6 (0110) a la
suma de 4 bits para evitar los 6 estados
inválidos y regresar el código a 8421. Si resulta
un carry cuando se suma el 6, simplemente
añada el carry al siguiente grupo de 4 bits.
Ejemplos donde la suma de los 4 bits es menor o
igual a 9:
Note que en cada caso la suma de cualquier
columna de 4 bits no excede de 9, y los
resultados son números BCD válidos
Ejercicio: Sumar los números BCD
1001000001000011 + 0000100100100101
Ejemplos del procedimiento en el caso de
sumas invalidas:
Ejercicio: Sumar los números BCD
01001000 + 00110100
Ejercicios
•
Cual es el peso binario de cada “1” en los siguientes
números BCD:
a) 0010 b) 1000 c) 0001 d) 0100
•
Convertir los siguientes números decimales a BCD:
a) 6 b) 15 c) 273 d) 849
•
Qué números decimales son representados por cada
código BCD:
a) 10001001 b) 001001111000 c) 000101010111
•
En la suma BCD, cuándo es inválida una suma de 4 bits?
Ejemplo
0010
+
0100
0110
0001
0110
0111
1111 111
0011 1001
0110 0111
1010 10000
Codigo BCD invalido →
Carry → Sumar 0110
2139
+
4667
6806
0010
+ 0100
+
0110
0001
0110
1
0111
0110
0110
1000
1000
1111 111
0011 1001
0110 0111
111
1010 10000
0110 0110
10000 10110
0000 0110
Codigo BCD invalido →
Carry → Sumar 0110
2139
+
4667
6806