Mediciones y propagación de errores

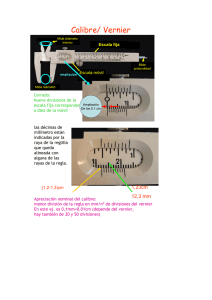
EXPERIENCIA 1
MEDICIONES DE LONGITUD, TIEMPO Y DENSIDAD
Para medir las cantidades básicas de longitud y tiempo el alumno utilizara instrumentos de medición
directa tales como una regla graduada, un calibre de vernier, un tornillo micrométrico y un cronometro;
en cambio, para medir la frecuencia de un movimiento periódico usara un estroboscopio que corresponde
a un instrumento de medición indirecta, los cuales entregan por analogía el valor de la cantidad a medir.
1. Objetivos.
1.1. Medir longitudes con una regla graduada.
1.2. Aprender a medir con un calibre de vernier.
1.3. Aprender a medir con un tornillo micrométrico.
1.4. Medir intervalos de tiempo con un cronometro.
1.5. Medir la frecuencia de un movimiento periódico con un estroboscopio
1.6. Determinar la precisión y el rango de un instrumento.
1.7. Obtener el error absoluto de una medición directa.
1.8. Calcular el error relativo de una medición directa.
1.9. Calcular el valor de una medición indirecta.
1.10 Calcular el error absoluto de una medición indirecta.
1.11. Determinar las cifras significativas y la precisión cuando se escribe el valor de una cantidad.
2. Descripción y fundamento teórico del calibre de vernier.
Es una regla graduada sobre la cual se desliza una corredera llamada vernier o nonio. Este
instrumento se utiliza para medir distancias entre superficies exteriores, interiores y profundidades;
dependiendo su precisión del número de divisiones del vernier, cuya escala esta grabada en la corredera.
Calibre de vernier
Figura 2.1. : Vernier
Regla móvil
Ľ
Regla fija
L
Figura 2.2. : Vernier métrico
1
0,9
2
1
3
2
4
3
4
5
6
5
7
6
8
7
9
8
1mm
p = 1[mm] /10 = 0,1 [mm]
10
9
Figura 2.3. : Vernier en pulgadas
0
1
2
3
0
4
5
6
7
8
½”
1”
P = (1” /16 )/8 = 1”/ 120
Figura 2. Tipos de vernier.
Tal como indica la figura 2.1., el vernier basa su funcionamiento en dos reglas graduadas, una
fija y una móvil o vernier. Si L ( > Ľ ) corresponde a la longitud de una división de la regla, Ľ a la
longitud de una división de las N divisiones de la regla móvil y ( N – 1 ) el numero de divisiones de la
regla fija que coinciden con las divisiones del vernier, se tiene : NĽ = ( N-L ) L, donde p = L – Ľ = L /
N corresponde a la precisión del calibre de vernier.
Por ejemplo, si la precisión de la regla fija es de 1 [ mm ] y el vernier está dividido en 20 partes,
la precisión del instrumento con vernier es de 0,05 [ mm ].
Los calibres de vernier mas usados son los graduados en milímetros y en pulgadas, figura 2.2. y
2.3.; sin embargo, se puede obtener fácilmente una lectura en cualquiera de ellos usando la relación:
x = A + N' ( L / N ), donde A corresponde a la lectura antes del cero del vernier, N' al numero de la
división del vernier que coincide con una línea de las regla fija, L a la precisión de la regla fija y N al
numero de divisiones del vernier.
3.- Vernier utilizado en el laboratorio.
4. Descripción y fundamento teórico del tornillo micrométrico.
Es un instrumento de mayor precisión que el calibre de vernier, se basa ene. Principio de que un
tornillo avanza longitudes iguales por cada vuelta que gira en torno de su eje. A medida que el tornillo
gira, el instrumento se abre y va descubriéndose una escala lineal grabada sobre su cuerpo principal.
Suponiendo que un tornillo tiene un paso de 1 [ mm ], cada vez que da una vuelta completa, éste avanza
sobre la escala lineal 1 [ mm ]; por lo tanto, si se divide la cabeza del tornillo en cien partes, las divisiones
se moverán con respecto a un punto fijo de la escala, correspondiéndole a cada paso de una división un
avance en la escala lineal de 0,01 [ mm ].
El paso ( mh ) o desplazamiento en la dirección longitudinal por vuelta completa de la cabeza
graduada del tornillo ( tambor ), es igual a 0,5 [ mm ] para un tambor con 50 divisiones; por consiguiente,
la precisión del tornillo micrométrico es de p = h /N = 0,5 [ mm ] / 50 = 0,01 [ mm ]. Del mismo modo, si
el paso de un tornillo graduado en pulgadas es h ( = 1” / 40 = 0,025” ) y la cabeza esta dividida en 25
partes, la precisión del tornillo es p = h / N = 0,025” / 25 = 0,001”. Por ultimo, debe destacarse que
cuando el tornillo esta cerrado, la lectura sobre la escala lineal debe corresponder a cero, de no ser así,
conviene registrar esta lectura.
Tornillo micrométrico.
5. Medición de la densidad de un cuerpo.
La densidad de masa ó simplemente  (= dm / dv ) es una propiedad intrínseca de un material y
concierne a la masa por unidad de volumen. Cuando un cuerpo es homogéneo su densidad puede
calcularse por la relación  = m / v, donde m representa la masa del cuerpo y v su volumen.
6. Investigación bibliográfica.
1. Teoría de errores.
1.1. Conceptos básicos.
1.2. Mediciones directas: Valor de una cantidad midiendo una sola vez.
1.3. Mediciones indirectas: Error de la función F ( x ) = Ax, donde A es una constante.
2. Unidades.
2.1.
2.2.
2.3.
2.4.
Unidades S.I. de tiempo.
Unidades S.I. de longitud.
Unidades S.I. de frecuencia.
Unidades S.I. de densidad.
3. Bibliografía.
3.1. Elementos de teoría de errores.
3.2. Apuntes de clases de la asignatura de Fisica I.
3.3. Textos recomendados en la asignatura de Fisica I.
2. Actividades del alumno. Mediciones
2.1.
2.2
2.3.
2.4.
2.5.
2.6.
2.7.
Miden la longitud de un objeto con una regla graduada, un calibre de vernier y un tornillo
Micrométrico.
Miden las dimensiones de un cilindro hueco con un calibre de vernier.
Miden el espesor de una hoja de papel con el tornillo micrométrico, midiendo una sola hoja.
Miden el espesor de N Hojas de papel con el tornillo micrométrico, para calcular el espesor de
una hoja.
Miden un periodo de oscilación de un péndulo con un cronometro.
Miden N periodos de oscilación de un péndulo con un cronometro, para calcular el periodo de
una oscilación.
Calculan la densidad de cualquier cuerpo homogéneo.