Ley de Darcy
Anuncio
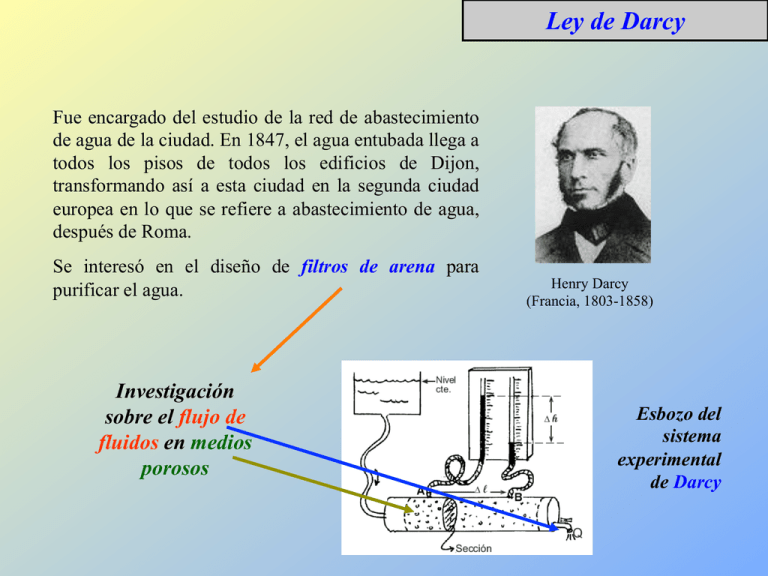
Ley de Darcy Fue encargado del estudio de la red de abastecimiento de agua de la ciudad. En 1847, el agua entubada llega a todos los pisos de todos los edificios de Dijon, transformando así a esta ciudad en la segunda ciudad europea en lo que se refiere a abastecimiento de agua, después de Roma. Se interesó en el diseño de filtros de arena para purificar el agua. Investigación sobre el flujo de fluidos en medios porosos Henry Darcy (Francia, 1803-1858) Esbozo del sistema experimental de Darcy Observando que se presentaba una caída de presión en el agua al pasar a través de una columna de arena, procede a cuantificar el fenómeno. Midió el gasto de agua Q y la caída de presión Δh , que pasa a través de la columna de arena de área transversal A: Gradiente de presión Caída de presión Gasto Obteniendo la siguiente relación fenomenológica: Q Δp ∝ A L El gasto por unidad de área, es proporcional al gradiente de presión Además, concluyó que la razón de proporcionalidad dependía del tipo de arena o medio poroso por donde fluía el agua. De esta forma, planteo lo siguiente: Δp Q = KA L Ley de Darcy Permeabilidad o Conductividad Hidráulica Experimentos subsiguientes sobre flujo en medio porosos, han permitido conocer sobre la dependencia de la constante de permeabilidad K: “No solamente depende del medio poroso sino también de las propiedades del fluido” Permeabilidad intrínseca ρg K =κ η porosidad, tortuosidad, temperatura…. Interesante: Q Δp = KD A L Q π R 4 Δp R 2 Δp Δp = = = KR A 8η L 8η L L Q Δp = KG A L Flujos ⇔ ¿Relación lineal? Ley de Darcy Ley de Poiseuille ¿Comportamiento General? Fuerzas I.2.0 Antes de Fluir Para no confundir con el tópico central de este tema que es el abordar a los fluidos cuando fluyen, en esta sección de entrada abordamos el movimiento de un fluido como un todo. Del Tema I.1, podemos resumir lo siguiente: ü Estudiamos a los fluidos en reposo. v=0 ü La descripción de los fluidos en reposo se sustenta en las Leyes de Newton. ∑ Fi = 0 i ü Las fuerzas de superficie que ejercen los fluidos en reposo deben ser compresoras y normales. ü La superficie de un líquido en reposo es horizontal. ü La distribución de presiones en el fluido satisface la Ecuación Fundamental de la Estática de Fluidos. dp = − ρ gdy p2 = p1 + ρ gh En el Tema I.2, hemos abordado a los fluidos ideales que fluyen por conductos y para ello hemos establecido lo siguiente: ü Flujo: Salida Entrada v≠0 ü La descripción del flujo se sustenta en la conservación de masa y las Leyes de Newton: ∑ Fi = ma i J M = cte ü La distribución de velocidades en el flujo satisfacen la Ecuación de Continuidad: Av = cte. ü La distribución de presiones dependiendo de la velocidad del flujo y la altura del mismo satisface la Ecuación de Bernoulli: dp = − ρ vdv − ρ gdy ¿Qué sucederá si ahora el recipiente que contiene al fluido se mueve aceleradamente? Veamos algunos situaciones y empecemos con la mas sencilla el Movimiento Vertical con Aceleración Uniforme: F 1 + F 2 + W = ma a Caso particular: Caída Libre F2 − F1 − mg = ma a Superficie Libre Plana (horizontal) ( p2 − p1 ) A = m ( a + g) ( p2 − p1 ) A = ρV ( a + g) ( p2 − p1 ) L2 = ρ L3 ( a + g) ( p2 − p1 ) = ρ ( a + g) L g ( p2 − p1 ) = 0 ⇒ p2 = p1 Movimiento de traslación horizontal con acelaración uniforme: Movimiento Uniformemente Acelerado t=0 Reposo Superficie Libre Plana (horizontal) Movimiento No-Estacionario Superficie Libre en Deformación t→∞ Movimiento Estacionario Superficie Libre Plana (inclinada) Movimiento Circular Uniforme: t=0 Reposo Superficie Libre Plana (horizontal) t→∞ Movimiento No-Estacionario Superficie Libre en Deformación Movimiento Estacionario Superficie Libre Curva (parabólica) Cuando los fluidos se mueven de la forma ilustrada anteriormente se dice que se mueven como cuerpos rígidos Partiendo de la aplicación de la Segunda ley de Newton y de las consideraciones sobre el tipo de movimiento acelerado, es posible obtener: - La forma de la distribución de presión en el interior del fluido. - La forma de la superficie libre que ahora NO necesariamente será horizontal. (Para mas adelante…según tiempos) Final del Tema I.2 y de la parte sobre Mecánica de Medios Continuos…!