Problemas de Placas Rectangulares. Método de Navier

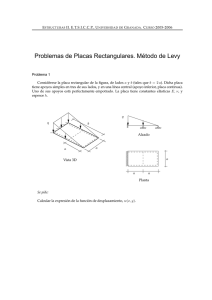
E STRUCTURAS II. E.T.S.I.C.C.P., U NIVERSIDAD
G RANADA . C URSO 2005-2006
DE
Problemas de Placas Rectangulares. Método de Navier
Problema 1
La placa rectangular, de lados a y b, y espesor t, simplemente apoyada en todo su contorno,
se encuentra sometida a una carga triangular, de valor máximo unitario “p”, como se indica en
la figura. Existe en el centro de la placa un soporte rectangular, de lados c y d, y longitud L,
empotrado en su extremo inferior, y unido a la placa en el punto superior del mismo.
p
p
t
L
Sección B-B’
A
c
b
d
B’
B
A’
a
Sección A-A’
Se pide:
1. Expresión general del desplazamiento de la placa suponiendo que no existe el soporte central. Evaluar numéricamente el desplazamiento para el punto central.
2. Desplazamiento en el punto central (evaluación numérica) al considerar la existencia del
soporte central.
Notas:
A efectos del ejercicio, se consideran las dimensiones c y d muy pequeñas respecto a los
valores a y b.
El pilar puede acortarse y flectar.
En los cálculos numéricos se tendrán en cuenta al menos los tres primeros términos del
desarrollo en serie de Fourier.
Datos:
a = 16 m ; b = 12 m; t = 0,20 m ; p = 4 ton/m2 ; ν = 0,2;
c = 0,3 m; d = 0,2 m; L = 10 m; E = 2 · 106 ton/m2
E STRUCTURAS II. E.T.S.I.C.C.P., U NIVERSIDAD
DE
G RANADA . C URSO 2005-2006
Problemas de Placas Rectangulares. Método de Navier
Problema 2
La placa de hormigón de la figura, de espesor t y dimensiones a × b, se encuentra inicialmente
simplemente apoyada en su contorno, sin otro tipo de sustentación adicional, y está sometida a
una carga uniforme de valor q. En esta situación, se observa que la flecha en el centro es excesiva.
Para reducirla, se coloca en el punto P (indicado en la figura) un cable de acero de longitud L y
sección A, perpendicular a la placa, al que se incorpora un mecanismo tensor con el que se puede
reducir su longitud.
L
3m
q
P
2m
b
a
Calcule, utilizando un sólo término del desarrollo en serie:
1. Flecha en el centro y en el punto P supuesto que no está colocado el cable.
2. Flecha en el centro y en el punto P supuesto que se coloca el cable, pero sin accionar el
tensor.
3. Acortamiento a aplicar al tensor para que la flecha en el centro sea la mitad que la del
apartado 1.
4. Acortamiento total y fuerza axil en el cable, en la situación final del apartado 3.
5. Momento torsor en el punto P bajo las condiciones del apartado 3.
Datos:
a = 5 m ; b = 4 m; t = 20 cm ; q = 80 kN/m2 ; ν = 0,2;
L = 6 m; E = 2 · 1010 N/m2 ; EAcable = 2 · 105 N
E STRUCTURAS II. E.T.S.I.C.C.P., U NIVERSIDAD
G RANADA . C URSO 2005-2006
DE
Problemas de Placas Rectangulares. Método de Navier
Problema 3
La placa rectangular de la figura, apoyada en sus cuatro lados, está sometida a una carga
uniforme q (en el sentido dibujado en la figura), en la mitad de su superficie (zona rayada).
Carga constante de valor q
A
B
b
a/2
a
Esquema en 3D
Calcular:
1. Expresión general de la flecha como función de x e y.
2. Giros en los puntos A y B (en la mitad de sus lados cortos).
Además del apoyo perimetral, la placa se une rígidamente a dos pilares de longitud L, y
sección c × d en los puntos A y B (se considera que la sección de los pilares es muy pequeña
comparada con las dimensiones a y b). En tal caso, se pide:
Calcular:
3. Giros en A y B, y flecha en el centro, considerando los pilares.
4. Diagrama de flectores y cortantes en el pilar B.
NOTA: Utilice sólo un término del desarrollo en serie para los cálculos numéricos.
Datos:
c = d = 0,6 m ; a = 8 m ; b = 6 m ; L = 4 m ; q = 5 kN/m2 ; E = 2 · 105 kp/cm2 ;
h = 0,2 m ; ν = 0,25
E STRUCTURAS II. E.T.S.I.C.C.P., U NIVERSIDAD
DE
G RANADA . C URSO 2005-2006
Problemas de Placas Rectangulares. Método de Navier
Problema 4
La placa rectangular de la figura está apoyada en sus cuatro lados y sometida a una carga
uniforme q, hacia abajo, sobre un tercio de la misma (ver figura). Se coloca después un apoyo
intermedio a mitad del lado b.
q
b
b/3
b/2
a
Calcular:
1. Expresión general (con letras) de la flecha supuesto que no existe el apoyo intermedio.
2. Flecha en el centro en este caso (numérico).
3. Cuando se coloca el apoyo intermedio, expresión general (con letras) de la reacción a lo
largo del mismo.
4. Resultante total de la reacción en el apoyo intermedio (numérico).
NOTA: Utilice sólo un término del desarrollo en serie para los cálculos numéricos.
Datos:
q = 5 kN/m2 ; a = b/2 = 3,5 m ; E = 2 · 105 kp/cm2 ; ν = 0,25 ; h = 20 cm