TEMA 4
Anuncio
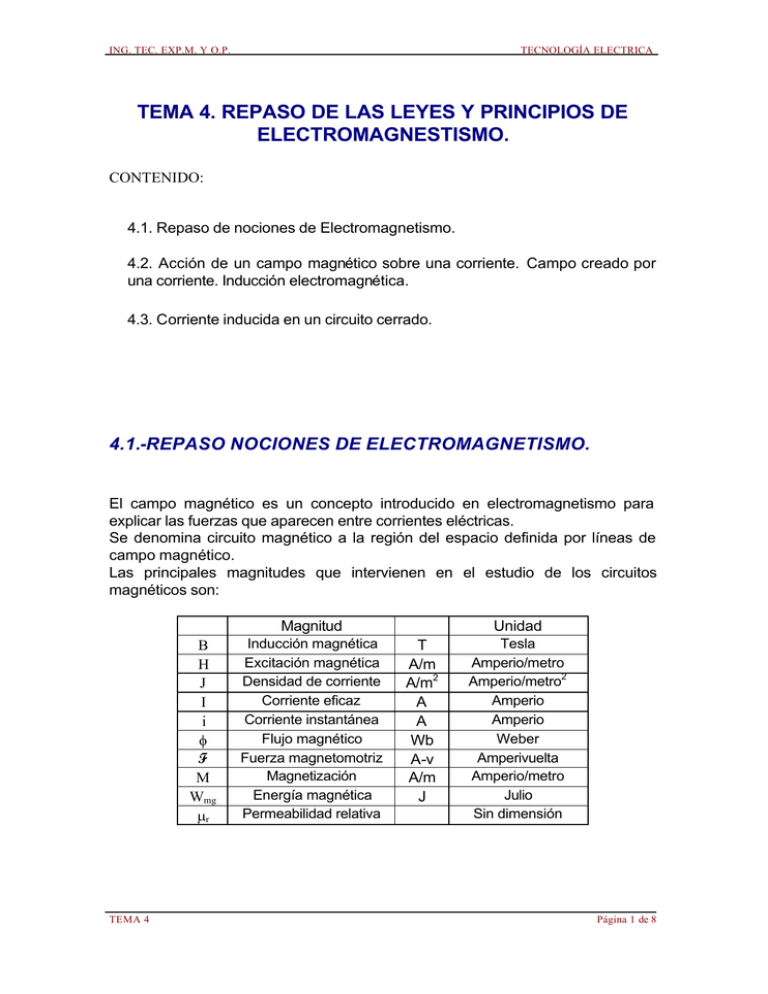
ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA TEMA 4. REPASO DE LAS LEYES Y PRINCIPIOS DE ELECTROMAGNESTISMO. CONTENIDO: 4.1. Repaso de nociones de Electromagnetismo. 4.2. Acción de un campo magnético sobre una corriente. Campo creado por una corriente. Inducción electromagnética. 4.3. Corriente inducida en un circuito cerrado. 4.1.-REPASO NOCIONES DE ELECTROMAGNETISMO. El campo magnético es un concepto introducido en electromagnetismo para explicar las fuerzas que aparecen entre corrientes eléctricas. Se denomina circuito magnético a la región del espacio definida por líneas de campo magnético. Las principales magnitudes que intervienen en el estudio de los circuitos magnéticos son: Magnitud B H J I i φ F M Wmg µr TEMA 4 Inducción magnética Excitación magnética Densidad de corriente Corriente eficaz Corriente instantánea Flujo magnético Fuerza magnetomotriz Magnetización Energía magnética Permeabilidad relativa Unidad T A/m A/m2 A A Wb A-v A/m J Tesla Amperio/metro Amperio/metro2 Amperio Amperio Weber Amperivuelta Amperio/metro Julio Sin dimensión Página 1 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA ANALOGÍAS FORMALES ENTRE CIRCUITOS ELÉCTRICOS Y MAGNÉTICOS MAGNITUD SÍMBOLO UNIDAD S.I. C.E. C.M. C.E. C.M. C.E. C.M. Intensidad de Flujo Magnético I Φ A Wb corriente Fuerza electromotriz Fuerza magnetomotriz Dif. de potencial eléctrico Resistencia Dif. de potencial magnético Reluctancia Conductancia Permeancia Resistividad ? Conductividad Permeabilidad Densidad de corriente Densidad de flujo Campo Eléctrico Excitación Magnética E V F U = ΦR = H l V V A-v Α−v R = ρ l/S G = σ S/l ρ σ j E R = l/µS P = µ S/l 1/µ µ B H Ω Ω -1 Ωm Ω -1 m-1 A m-2 V m-1 Ω -1 s-1 Ωs -1 -1 Ω s m Ω s m-1 T = Wb m-2 A-v m-1 DIFERENCIAS DESTACABLES Un circuito magnético tiene un comportamiento NO LINEAL, esto es, la permeabilidad no es constante, sino que depende de H (o de B). Por ello hay que conocer la curva de imanación o de magnetización B = f (H), con la consiguiente aparición de Histéresis En los circuitos magnéticos hay que tener en cuenta la existencia de FLUJOS DE FUGAS o de dispersión. LAS ECUACIONES UTILIZADAS EN EL ANÁLISIS DE LOS CIRCUITOS MAGNÉTICOS PROCEDEN DEL ESTUDIO DE ELECTROMAGNETISMO, SON: Ley circuital de Ampere: viene dada por la expresión: ∫ Hdl = ∫ Jds c s Si se cumple que H es constante para todos los puntos del circuito magnético de longitud l, definido por c, y además tenga la dirección del elemento dl, la integral se reduce a Hl. Si la densidad de corriente eléctrica se obtiene por una serie de espiras (N) recorridas por una corriente i, que atraviesan la curva c, la segunda integral se reduce a Ni. Quedará: Hl = Ni TEMA 4 Página 2 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA Al producto Ni se le denomina fuerza magnetomotriz (f.m.m.) (F) Ley del flujo magnético: viene dada por la expresión: ∫ Bds = 0 s que se puede expresar, si la inducción es perpendicular al elemento magnético como: φ = B⋅ A Curva de magnetización del material: Según el material con el que está fabricado el circuito magnético existirá una relación entre B y H. Esta relación es la permeabilidad, que en la hipótesis de que fuera constante, la relación entre B y H será: B = µH Ley de inducción de Faraday: Cuando un conductor se mueve en un campo magnético uniforme, los portadores de carga experimentan una fuerza magnética (qv x B). Esta fuerza magnética da lugar a corrientes inducidas en el circuito del conductor. Si ahora consideramos una bobina o espira estática, con forma y orientación fijas, (v =0), la fuerza electromagnética que actúa sobre una partícula cargada será: F = q (E + v x B) De forma que si existe un campo eléctrico E, actuaría una fuerza eléctrica F sobre los portadores de carga aunque estuvieran inicialmente en reposo. Esta fuerza eléctrica producirá un campo eléctrico cuando el campo magnético varíe con el tiempo ( B = f(t) ⇒ E ≠ 0 ) De lo anterior deducimos que un campo magnético cuyo módulo aumenta, induce una corriente en un circuito o espira. El campo eléctrico tangencial inducido mueve los portadores de carga a lo largo de la espira o circuito circular mediante la fuerza eléctrica F = q E. TEMA 4 Página 3 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA Este campo eléctrico produce una fuerza electromotriz inducida (trabajo por unidad de carga de la fuerza F) representada por: e= dΦ B W F ⋅ dl =∫ = ∫ E ⋅ dl = q q dt relación expresada como la Ley de Faraday en su forma fundamental. En el caso de una bobina con N espiras, atravesada por un flujo magnético φ variable con el tiempo, hace que aparezca una tensión inducida de valor: e= N dφ dt la cual provoca una corriente que se opone a la variación de flujo (Ley de Lenz). Energía acumulada en el campo magnético: en toda región del espacio donde exista un campo magnético existe una energía acumulada por unidad de volumen dada por: dWmg = dv B2 2µ Circuitos magnéticos deformables. En numerosos dispositivos utilizados en maniobra (relés, contactores, etc.), así como en electroimanes y algunos tipos de motores (p.e., motores paso a paso de reluctancia variable) se utiliza la fuerza de atracción magnética para conseguir un desplazamiento mecánico. La energía, por unidad de volumen, almacenada en un circuito magnético, es: w= ∫ H dB Si el circuito magnético no está saturado (µ = cte.) y la inducción magnética varía desde cero hasta B, la expresión anterior se escribe: w= TEMA 4 1 µ0 ∫ B 0 B dB = 1 B2 2 µ0 Página 4 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA Si una parte del circuito magnético se deforma, se produce una variación de la energía almacenada en el campo magnético. Aplicando el Principio de los trabajos virtuales, se determina la fuerza (p.e., entre dos caras adyacentes de un entrehierro en un circuito magnético): F = - Φ2 dR B2 S = 2 dx 2 µ0 donde B es la inducción magnética en el entrehierro y S la sección recta del mismo. El signo negativo indica que la energía aumenta cuando dx es negativo, dicho de otra forma: “la fuerza es siempre de atracción”. Otra conclusión de interés es la siguiente: “Los elementos de un circuito magnético deformable se desplazan de forma que disminuya la reluctancia total del circuito, o sea que la posición de equilibrio estable coincide con un mínimo de la reluctancia”. TEMA 4 Página 5 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA 4.2. Acción de un campo magnético sobre una corriente. Campo creado por una corriente. Inducción magnética. Circuitos eléctricos con acoplamiento magnético. Dos circuitos están acoplados magnéticamente cuando están atravesados por un flujo común. Si éste es variable en el tiempo la energía puede transferirse de un circuito al otro (“efecto transformador”). Analizaremos el acoplamiento magnético entre el primario y el secundario de un trafo monofásico de columnas con devanados separados: FIG. 1.1 Φ 12 : Φ 21 : Φ 11 : Φ 22 : Φ1 : Φ2 : TEMA 4 Valor medio por espira del flujo que crea el devanado primario y que atraviesa al secundario. Valor medio por espira del flujo que crea el secundario y que atraviesa al primario. Valor medio por espira del flujo de fugas o de dispersión del primario. Valor medio por espira del flujo de fugas del secundario. Valor medio por espira del flujo propio del primario. Valor medio por espira del flujo propio del secundario. Página 6 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA Φ 1 = Φ 12 + Φ 11 Φ 2 = Φ 21 + Φ 22 Los coeficientes de autoinducción de primario y secundario y el coeficiente de inducción mutua son: L1 = N1 Φ 1 / i1 L2 = N2 Φ 2 / i2 M = N1 Φ 21 / i2 = N2 Φ 12 / i1 Las tensiones inducidas por autoinducción e inducción mutua son: e1L = N1 dΦ 1/dt = L1 di1/dt e2L = N2 dΦ 2/dt = L2 di2/dt e1M = N1 dΦ 21/dt = M di2/dt e2M = N2 dΦ 12/dt = M di1/dt El coeficiente de acoplamiento: Ka = Φ12 Φ21 = Φ1 Φ2 M L1 L 2 Para aplicar correctamente la 2ª Ley de Kirchhoff, conviene revisar el significado de las marcas con puntos (terminales de igual polaridad instantánea, teniendo en cuenta sólo la inducción mutua) y aplicar la siguiente regla práctica; “ Si las dos corrientes penetran o salen (ambas) por terminal marcado por punto, en una misma ecuación, el signo de un término en M es el mismo que el signo de un término en L. Si una corriente penetra y otra sale ...”. Naturalmente que el signo de un término de autoinducción es siempre el mismo que el de caída óhmica. En el esquema del trafo propuesto: v1 = v2 = R1 i1 + L1 di1/dt - M di2/dt - R2 i2 - L2 di2/dt + M di1/dt Si admitimos que las magnitudes son idealmente alternas senoidales, la notación compleja que refleja las ecs. básicas del transformador quedan: V1 = R1 I1 + j L1ω I1 - j M ω Ι 2 V2 = -R2 I2 - j L2ω I2 + j M ω I1 TEMA 4 Página 7 de 8 ING. TEC. EXP.M. Y O.P. TECNOLOGÍA ELECTRICA 4.3. Producción de una corriente inducida en un circuito cerrado. Hemos visto que cuando varía el flujo de campo magnético a través de un circuito en forma de espira aparece una fuerza electromotriz inducida en el mismo dada por la ley de Faraday: e= N dφ dt Consideraremos ahora que el campo magnético está creado por la propia corriente que circula por una espira plana como se muestra en la figura: i(t) e Esta corriente producirá un campo magnético en las cercanías de la espira, existiendo un flujo de campo magnético atravesando la espira. Al ser la intensidad variable con el tiempo, el flujo también por lo que aparecerá una fuerza electromotriz inducida. Dado que ΦB = L i donde la constante de proporcionalidad L es la Autoinductancia de la espira, aplicando la ley de Faraday obtenemos: eL = -L di/dt para una bobina de N vueltas tendremos NΦ B = L i; eL = -NL di/dt y en definitiva L = µ0 n2S l siendo n el número de vueltas por unidad de longitud, S el área perpendicular a la espira, l la longitud de l solenoide y µ0 la constante de permeabilidad. TEMA 4 Página 8 de 8






