TALLER # 1 ESTÁTICA

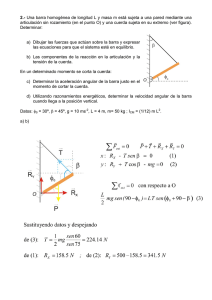
TALLER # 1
ESTÁTICA
1. Una barra homogénea de 200N de peso y longitud L se apoya sobre dos superficies como
se muestra en la figura 1. Determinar:
a. El valor de la fuerza F para mantener la barra en la posición indicada.
Respuesta: F = 75N
b. Las reacciones en los apoyos. Respuesta: NA = 156.7N y NB = 86.6N
Figura 1
2. Una barra homogénea de 369N de peso y longitud L está articulada en su extremo A y se
apoya en su extremo B sobre una superficie lisa tal como se muestra en la figura 2.
Determinar la reacción en la articulación. Respuesta: RA = 321.2N y NB = 217N
Figura 2
3. Una barra homogénea de pero P y longitud L está en equilibrio en una cavidad semiesférica
lisa de radio R tal como se muestra en la figura 3. Determinar el valor del ángulo de
equilibrio α si L=3R. Respuesta: 23.20
Figura 3
4. Una barra homogénea de 200N de peso y longitud L se apoya sobre dos superficies como
se muestra en la figura 4. La superficie inclinada es lisa y la horizontal rugosa. Determinar:
a. El valor de la fuerza de rozamiento en A para mantener la barra en equilibrio en la
posición indicada. Respuesta: fr = 75N y NB = 86.6N
b. El coeficiente de rozamiento mínimo para el equilibrio. Respuesta: µ = 0.48
Figura 4
5. La barra homogénea AB de la figura 5, de masa m y longitud L, se mantiene en equilibrio
apoyada en el borde C de un soporte, tal que AC=L/5 y mediante un cable unido a su
extremo en B. Determinar: el valor mínimo del coeficiente de rozamiento µ para que la
barra se mantenga en equilibro en la posición indicada. Respuesta: µ = 0.62
Figura 5
6. Una barra homogénea de peso P y longitud L se apoya por su extremo A sobre un suelo
horizontal rugoso, coeficiente de rozamiento µ, y su extremo B está unido a un cable, que
pasa por una polea, el cual le ejerce una fuerza F que mantiene la barra en la posición
indicada en situación de movimiento inminente. Determinar el valor de µ en función de α y
β. Respuesta:  
1
tan   2 tan 
Figura 6
7. Una barra homogénea de pero P = 90N y longitud L se mantiene en equilibrio apoyada por
su extremo A sobre una pared vertical rugosa; su extremo B está unido a un cable fijo a la
pared en el punto C, cuya longitud es 1.57L que forma con la pared un ángulo de 220.
Determinar: el ángulo α, la tensión del cable y la fuerza de rozamiento.
Respuestas: α = 540, T = 31N y fr = 61N
Figura 7
8. Una barra uniforme de peso P y longitud L está articulada en su extremo A y se apoya
sobre un disco liso de radio R y peso Q, tal como se muestra en la figura 8. El disco se
apoya sobre una superficie horizontal lisa y su centro unido a la articulación mediante un
cable. Determinar la tensión del cable y la reacción en la articulación.
Respuesta: T 
NB 
 2R2  R
1  2 
a a
a2  R2 
PL
y
 2R2 
1  2 
a 
2 a2  R2 
PL
Figura 8
R  N B2  P 2  2PN B cos  ; con
9. Una escalera de peso P = 120N se apoya en una pared vertical lisa y sobre un suelo
horizontal rugoso como se muestra en la figura 9. El coeficiente de rozamiento es µ=0.5.
La distancia entre peldaños es de 30cm. Una persona de peso Q = 700N asciende por la
escalera. Determinar hasta que peldaño puede subir sin que la escalera se caiga.
Respuesta: 5 peldaños
Figura 9
10. Un cilindro de peso P y radio R se encuentra en equilibrio en la posición indicada en la
figura 10. Se considera que todas las superficies son lisas. Determinar: la reacción en la
articulación y la tensión del cable.
Figura 10
11. Un cilindro de peso Q y radio R se apoya boca abajo sobre una superficie horizontal tal
como se muestra en la figura 11. En su interior hay dos esferas de radio r y peso P cada
una. Determinar el peso del cilindro para que éste no vuelque. Todas las superficies se
consideran lisas.
Figura 11
12. Una barra homogénea AB de peso Q descansa en el punto A sobre una pared vertical
áspera. El coeficiente de rozamiento entre la barra y la pared es igual a µ. En el punto B la
barra se apoya sobre un piso horizontal liso. La barra se mantiene en equilibrio mediante el
hilo BC que pasa por la polea ideal C. Si del extremo del hilo se suspende un peso P,
determine los limites dentro de los cuales puede variarse la magnitud del peso P sin alterar
el equilibrio de la barra. Respuesta:
Q
Q
P
2  tan    
2  tan    
Figura 12
13. Imagine que está tratando de subir una rueda de bicicleta de masa m y radio R a una acera
de altura h; para ello, aplica una fuerza horizontal F. Qué magnitud mínima de F logra
subir la rueda si la fuerza:
a. Se aplica en el centro de la rueda.
Respuesta: F  mg
2 Rh  h 2
2R  h
b. Se aplica en la parte superior de la rueda.
Respuesta: F  mg
2Rh  h 2
Rh
c. ¿En cuál caso se requiere menos fuerza?
Figura 13
14. Un albañil de 75 kg camina sobre un tablón de 3 m de largo y 80 kg apoyado sobre dos
vigas distantes 2 m, tal como indica la figura 14. ¿Cuál es la máxima distancia x que puede
recorrer, sin que caiga? Respuesta: x= 0.53m
Figura 14
15. Determinar la tensión en el cable AB que impide que el poste AC de 18kg de masa deslice.
Suponer que todas las superficies son lisas. Respuesta: T = 46.2N
Figura 15
16. Un hombre de 60 kg que camina a 2 m/s atraviesa un tabla de 30 kg y 10 m de largó
a. ¿Cuál es la fuerza sobre el soporte B en función del tiempo?
b. Si la máxima fuerza que puede resistir B es 490N ¿Cuándo y dónde caerá al río el
hombre?
Considerar que el peso del hombre siempre actúa en dirección de la vertical que pasa por su
centro de masa. Respuesta: a) FB = (12t +15) 9.8N, b) t = 2.92s, x = 5.83 m de A.
Figura 16
17. En la figura 17 se tiene una barra homogénea de 16 m de longitud colocada entre paredes
lisas separadas por 1 m. Hallar el valor de  para la posición de equilibrio. Respuesta: 600
Figura 17
18. Una barra AB de longitud L y peso W, está soportada por un pasador en A y una cuerda en
B. Sostiene una carga de peso P suspendida de su extremo. Hallar la tensión en la cuerda y
las componentes de la reacción en A.
Respuesta: T 
 P  W / 2 ;
sen
Rx   P  W / 2  cot  ; Ry 
Figura 18
W
2
19. Una escalera homogénea de peso W está apoyada en un piso y una pared lisos y se
sostiene con una cuerda como se indica en la figura.
a. Calcule la tensión de la cuerda en términos de W, L, d.
b. Si la máxima tensión que resiste la cuerda es W/3, ¿cuál es la máxima distancia
d a la que puede colocarse la cuerda?
Respuesta: T 
LW
;
2 3L  d 

3
d  1 
 L
2


Figura 19
20. Un semáforo cuelga de una estructura como la que se ve en la figura 20. El poste
uniforme de aluminio AB tiene 7.5 m de longitud y 8 kg de masa. El semáforo es
de 11 kg. Calcule la tensión del cable horizontal sin masa CD y las componentes
vertical y horizontal de la fuerza que el pivote A ejerce sobre el poste de aluminio.
Respuesta: T = Rx = 74.48N y Ry = 186.2N
Figura 20