+ = ji para ij ji para i , 1 , 2

ESCUELA ACADÉMICO PROFESIONAL DE CIENCIAS CONTABLES Y FINANCIERAS
EXAMEN FINAL
MATEMÁTICA III
Nombres y Apellidos:___________________________________________________________________________________________
FECHA: 05/12/2014
1) Dadas las matrices A = ( aij)3x3
aij =
i2
y B = (bij)3x3, donde :
+ 2j + 3
y
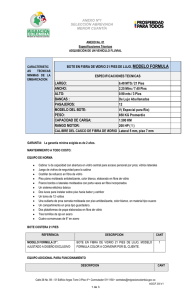
 i 2 , para...i  j
bij = 
1  ij , para...i  j
a) Hallar 𝐴 y 𝐵
A=
y
B=
b) Calcular 4𝐴 − 3𝐵𝑇
4𝐴 − 3𝐵𝑇 =
c) Calcular 𝐵. 𝐴𝑇
𝐵. 𝐴𝑇 =
d) Calcular el determinante de 𝐵. 𝐴𝑇
det(𝐵. 𝐴𝑇 ) = 0
2) Un contratista ha aceptado pedidos para cinco casas con estilo rústico, siete con estilo moderno y 12
con estilo colonial. Entonces, sus pedidos pueden representarse por la matriz
𝑄 = [5 7 12]
Además las materias primas que se usan son acero, madera vidrio, pintura y mano de obra, donde el
número de unidades de cada materia prima que se utilizará en cada tipo de casa están dadas por la
matriz:
𝑅ú𝑠𝑡𝑖𝑐𝑜
𝑅 = 𝑀𝑜𝑑𝑒𝑟𝑛𝑜 [
𝐶𝑜𝑙𝑜𝑛𝑖𝑎𝑙
𝐴𝑐𝑒𝑟𝑜
30
46
14
𝑀𝑎𝑑𝑒𝑟𝑎
34
20
26
𝑉𝑖𝑑𝑟𝑖𝑜 𝑃𝑖𝑛𝑡𝑢𝑟𝑎 𝑀𝑎𝑛𝑜 𝑑𝑒 𝑜𝑏𝑟𝑎
20
7 17
16
9 31]
24
5 13
Cada fila indica la cantidad de materia prima necesaria para un tipo de casa; cada columna indica la
cantidad necesaria de materia prima para cada tipo de casa.
ESCUELA ACADÉMICO PROFESIONAL DE CIENCIAS CONTABLES Y FINANCIERAS
Suponga que el contratista desea tomar en cuenta el costo de transportar la materia prima al lugar de
la construcción, así como el costo de compra. Suponga que los costos están dados en la matriz que se
da a continuación:
𝐶𝑜𝑚𝑝𝑟𝑎
𝑇𝑟𝑎𝑛𝑠𝑜𝑝𝑟𝑡𝑒
2500 45
1200 20
𝐶=
800 30
150
5
[1500 0 ]
El contratista desea calcular:
a) Encuentre una matriz cuyas entradas proporcionen los costos de compra y de transporte de los
materiales para cada tipo de casa.
𝑅𝐶 =
b) Encuentre la matriz QRC cuya primera entrada dé el precio de compra total y cuya segunda
entrada dé el costo total de transporte.
𝑄𝑅𝐶 =
1
c) Sea 𝑍 = [ ] calcule QRCZ, que proporciona el costo total de materiales y transporte para todas las
1
casas que serán construidas.
𝑄𝑅𝐶𝑍 =
3) Un agente de bolsa vendió a un cliente 200 acciones tipo A, 300 tipo B, 500 tipo C y 250 tipo D. Los
precios por acción de A, B, C y D son $100, $150, $200 y $300, respectivamente. Escriba una matriz que
represente el número de acciones compradas de cada tipo. Escriba una matriz que represente el precio
por acción de cada tipo. Encuentre el costo total de las acciones.
200
300
]
𝐴𝑐𝑐𝑖𝑜𝑛𝑒𝑠 = [
500
250
𝑃𝑟𝑒𝑐𝑖𝑜𝑠 = [100 150 200 300]
𝑐𝑜𝑠𝑡𝑜 𝑡𝑜𝑡𝑎𝑙 = [240000]
ESCUELA ACADÉMICO PROFESIONAL DE CIENCIAS CONTABLES Y FINANCIERAS
4) Un contratista puede adquirir las cantidades requeridas de madera, ladrillos, concreto, vidrio y pintura
de cualesquiera tres proveedores. Los precios que cada proveedor fija a cada unidad de estos cinco
materiales están dados en la matriz A.
8 5 7 2 4
𝐴 = [9 4 3 2 5 ]
9 5 6 1 5
En esta matriz, cada renglón se refiere a un proveedor y las columnas a los materiales, en el orden
listado arriba. El contratista tiene la política de adquirir todos los materiales requeridos en cualquier
obra particular al mismo proveedor para de minimizar los costos de transportación. Hay tres obras en
construcción actualmente: la obra I requiere 20 unidades de madera, 4 de ladrillos, 5 de concreto, 3 de
vidrio y 3 de pintura; la obra II requiere 15, 0, 8, 8 y 2 unidades, respectivamente; y la obra III requiere
30, 10, 30, 10 y 12 unidades, respectivamente. Disponga esta información en una matriz B de orden 5 ×
3 y forme la matriz producto AB.
Interprete los elementos de este producto y úselos con el propósito de decidir cuál proveedor debería
usar en cada obra.
8 5 7 2 4
𝐴 = [9 4 3 2 5 ]
9 5 6 1 5
20 15 30
4
0 10
𝐵= 5
8 30
3
8 10
[3
2 12]
𝐴. 𝐵 =
5) En los problemas siguientes, resuelva el sistema dado (si la solución existe) usando el método de
reducción de renglones.
{p1,q1}
{x11,x22,x3-1}