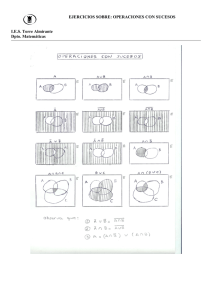
Operaciones con sucesos A = B A ⋂ B A ∪ B A B − A = B − A ⋂ B B
Anuncio

www.clasesalacarta.com
Matemáticas – A _ 1º Bach.
Probabilidad
Operaciones con sucesos
Igualdad de sucesos
Intersección de
sucesos (Y)
A=B
Incompatibles
Unión de sucesos (Ó)
Diferencia de
Sucesos
Suceso Contrario
AB
B−A=B−AB
B−A= B
AB
AB=
Propiedades de las operaciones con sucesos
Intersección
Unión
Conmutativa
A∩B=B∩A
A∪B=B∪A
Asociativa
A ∩ (B ∩ C) = (A ∩ B) ∩ C
A ∪ (B ∪ C) = (A ∪ B) ∪ C
Idempotente
A∩A=A
A∪A=A
Simplificación
A ∪ (A ∩ B) = A
A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Elemento neutro
A ∩ (A ∪ B) = A
A ∩ (B ∪ C) = (A ∩ B) ∪
(A ∩ C)
A∩E=A
Absorción
A ∪ = A
A∪E=A
Distributiva
A∪=A
Leyes de De Morgan
Probabilidad
Regla de Laplace
Propiedades
1. 0 P(A) 1
2. P(E) = 1
3. A
B = : P(AB) = P(A)+P(B)
Probabilidad condicionada
Consecuencias de la definición
1. P( ) = 1 – P(A)
2. P() = 0
3. P(AB) = P(A) + P(B) – P(AB)
4. P(ABC) = P(A)+P(B)+P(C)−P(AB)−P(AC)−P(BC)+P(ABC)
5. A B: P(A) P(B)
6. S E
t yS
{x1, x2,…, x }: S
X1 + x2 +…+ x
Sucesos independientes
Experimentos compuestos
P(AB) = P(A) · P(B)
Teorema de la probabilidad total
Teorema de Bayes
P(AB) = P(B) · P(A/B)
P(B)=P(A1)·P(B/A1)+P(A2)·P(B/A2 +…+P(An)·P(B/An)
1
1
+
2
2
+
+