Modelado termal 1D de la cuenca oriental de Venezuela

UNIVERSIDAD SIMÓN BOLÍVAR
INGENIERÍA GEOFISICA
Por :
Br. Melissa J. Hernández Quijada
Presentado ante la Ilustre Universidad Simón Bolívar
Como requisito parcial para optar al título de
Ingeniero Geofísico
Realizado con la asesoría de los profesores Carlos Izarra y María Inés Jácome
Sartenejas, Marzo del 2006
Este trabajo ha sido aprobado en nombre de la Universidad Simón Bolívar por el siguiente
jurado calificador:
ghgMelissa Hernandez Quijada Hola Chao
Presidente
ghgMelissa Hernandez Quijada Hola Chao
Melissa Hernandez Quijada Hola Chao
ghgMelissa Hernandez Quijada Hola Chao
Por: Br. Melissa J. Hernández Quijada
RESUMEN
El presente trabajo de grado pretende continuar el estudio de Fernández (2004), el cual reveló
que hacia el noreste de la Subcuenca de Guárico existe una anomalía termal considerable, en este
sentido se analizó cuatro zonas representativas de la Cuenca Oriental de Venezuela: Guarico, Norte,
Centro y Oeste de Maturín. Se construyeron columnas litológicas y perfiles de temperaturas
característicos en cada zona a partir de información de 57 pozos y 4 secciones sísmicas previamente
interpretadas y suministradas por PDVSA Exploración. Se realizaron curvas de subsidencia, bajo la
técnica de retroevolución (Backstripping), en las cuales se identificaron las tectonosecuencias de margen
pasivo y margen activo en cada uno de los modelos. La subsidencia resulto diacrónica y más joven en el
Este que en el Oeste. También se cuantifico las tasas de subsidencia de los sedimentos en cada zona,
asociándose las tasas más altas al margen activo y las más bajas al margen pasivo. En Guárico se
observa un levantamiento o rebote isostático de edad Oligoceno que posiblemente este relacionado a la
anomalía termal y/o al desarrollo o reactivación de fallas normales. En Maturín Norte también se observa
un levantamiento o rebote isostático en el Mioceno Temprano asociado al emplazamiento y erosión del
Corrimiento de Pirital, ubicado para entonces al oeste del área.
Para la realización del modelado termal se utilizo el algoritmo FDTHERM y esta basado en
aproximaciones de diferencia finita de continuidad y ecuaciones de transporte para temperatura. El
algoritmo necesita que se le definan condiciones de bordes, valores de conductividad termal, calor
específico y densidades. Adicionalmente se consideró otros parámetros termales como: producción de
calor, flujo de calor del manto y velocidades de fluidos, los cuales permitieron un mejor ajuste de las
curvas observadas y calculadas. Se plantean principalmente dos hipótesis, que podrían explicar la
anomalía termal de Guarico: una de carácter local relacionada a entrampamiento de gas, y la segunda
de efecto regional plantea que probablemente un ascenso pasivo del manto caliente (adelgazamiento
cortical, 25 km) o la existencia de una fuente de calor cortical podría estar aumentado los valores de
temperatura en el área. Las regiones de Maturín Norte y Centro muestran un comportamiento termal
normal, los modelos generados ajustaron satisfactoriamente las geotermas observadas.
ii
En primer lugar quiero agradecer a Dios, a la virgen de Betania y a la virgen del Valle, por
permitirme estudiar es una USB y por ayudarme durante todos mis años de estudios, en los cuales
siempre les he suplicado salir bien y culminar con éxito.
Gracias a mis padres: por todo su apoyo y compresión, no solo durante la elaboración de esta
tesis, sino durante todos mis años de estudios, los cuales no hubiera realizado sin ellos....Gracias por
soportar mi mal humor y mi falta de tiempo.
Gracias a mis tutores Carlos y María Inés por su guía, apoyo, comprensión y por todo el tiempo
dedicado a este trabajo...y por siempre esperar más...eso me motivo cada vez más a hacer un mejor
trabajo. Gracias en especial a Carlos por su buen humor y por sus palabras de aliento en todo momento y
Gracias a María Inés por ser tan crítica, exigente y comprensiva.
Gracias Willy por ser tan buen compañero de tesis y amigo...de verdad te agradezco mucho por
todos esos favores que me has hecho desde que te conocí...Gracias por ser tan especial no solo conmigo
sino con todo el mundo..tienes un corazón muy grande y bonito...y Un millón de gracias por las 500mil
veces que me prestaste tu lapto.
Quiero agradecer a mi gran amiga Eileen, gracias por escucharme y por acompañarme en esos
momentos tan difíciles para mi, fuiste un gran apoyo tanto para la culminación como para comienzo de
nuevas etapas en vida, me has dado muy buenos consejos y de corazón sin esperar nada a cambio,
gracias....sin tu apoyo para en aquellos momentos tan abrumantes en mi vida personal tal vez no hubiera
logrado terminar este trabajo.
Irma, gracias por todo el tiempo que me acompañaste durante la tesis, por todo tu apoyo, amistad
y ayuda... el tiempo que estuviste en la sala fue muy agradable trabajar contigo....y a partir de ahí nos
convertimos en muy buenas amigas.
iii
No se me puede olvidar darle mis más sinceros y afectuosos agradecimientos a Omar, un gran
amigo y compañero de tesis, eres una persona muy especial que esta siempre dispuesta a ayudar a los
demás, gracias por escuchar mis rabietas y tratar de calmarlas.
Gracias Max por siempre responder a mis gritos de auxilio y a todas mis preguntas. Gracias por
por tus palabras de aliento.
También quiero agradecer especialmente a Humberto y Giovanni, amigos de la UCV, por
haberme suministrado parte de la información bibliográfica utilizada en esta tesis, además de contarme
sus experiencias y motivarme cada vez a realizar un buen trabajo.
Por último, pero no menos importantes deseo agradecer a mis buenas amigas y amigos: Gise ,
Vero, Diane, Palo, Pedro, Melisota y Lisbeth por su apoyo, compañía y consejos durante todos nuestros
años de estudios juntos. Gracias especialmente a Manuel por siempre estar dispuesto a ayudarme en lo
que fuera y escuchar todos mis problemas.
iv
INDICE DE TABLAS DE FIGURAS
viii
APÉNDICE A.
122
APÉNDICE B.
136
CAPITULO 1: INTRODUCCIÓN
1
1.1 Introducción
1
1.2 Objetivos
2
1.3 Localización del área de estudio
3
1.4 Metodología
4
1.5 Trabajos previos
5
CAPITULO 2: MARCO TEÓRICO
7
2.1 Conceptos básicos
7
2.1.1 Temperatura
7
2.1.2 Trasferencia de Calor
8
2.1.3 Geoterma
9
2.1.4 Flujo de Calor
9
2.1.5 Consideraciones termales de la litosfera oceánica
10
2.1.6 Consideraciones termales de la litosfera continental y la radioactividad
12
2.2 Modelado Numérico Termal
15
CAPITULO 3: CUENCAS SEDIMENTARIAS
19
3.1 Origen y Evolución de las Cuencas Sedimentarias
19
3.1.1 Cuencas en regímenes extensivos
19
3.1.1.1 Modelo de extensión litosférica
19
3.1.2 Cuencas en regímenes compresivos
21
3.2 Paleotemperaturas
24
3.2.1 Efecto de la Conductividad Termal
24
3.2.2 Efecto de la Producción de Calor Interno en los sedimentos
25
3.2.3 Efecto de la circulación de agua
26
3.3 Características Paleogeotermales de las Cuencas Sedimentarias
26
3.3.1 Márgenes Pasivo
26
3.3.2 Cuenca Hipertermales
27
v
3.3.3 Cuencas Hipotermales
27
3.4 Retro-evolución (Backstripping)
30
3.4.1 Carga Sedimentaria
33
3.4.2 Subsidencia Tectónica
35
3.4.3 Subsidencia Termal
36
3.5 Isostacia Local y Regional
38
CAPITULO 4. MARCO GEOLÓGICO Y TECTÓNICO
40
4.1 Evolución Geológica del Caribe
40
4.2 Cuenca Oriental de Venezuela
46
4.3 Evolución Tectono-Estratigráfica de la Cuenca Oriental
50
4.3.1 Paleozoico
50
4.3.2 Fase de Ruptura
50
4.3.3 Margen Pasivo
51
4.3.4 Margen Activo
53
4.4 Estructuras principales de la Cuenca Oriental de Venezuela
60
4.4.1 Cordillera de la Costa
60
4.4.2 Surco de Guárico
62
4.4.3 Corrimiento frontal de Guárico
62
4.4.4 Cinturón de plegamientos y cabalgamientos de la Serranía del Interior Oriental
63
4.4.5 Falla de Urica
63
4.4.6 Corrimiento de Pirital
64
4.4.7 Graben de Espino
64
4.4.8 Corrimiento de Anaco
64
CAPITULO 5: ANÁLISIS DE SUBSIDENCIA
66
5.1 Integración de datos
66
5.1.1 Maturín Norte
67
5.1.2 Maturín Centro, Maturín Oeste y Guarico
68
5.2 Resultados y Análisis
71
5.2.1 Maturín Norte
71
5.2.2 Maturín Centro
74
5.2.3 Maturín Oeste
77
vi
5.2.4 Guarico
79
5.3 Incertidumbres asociadas a la retro-evolución
82
CAPITULO 6:
84
6.1 Introducción
84
6.2 Breve descripción del proceso de modelado
85
6.3 Perfiles de Temperatura
85
6.4 Resultados y Análisis Termales
88
6.4.1 Maturín Norte
88
6.4.2 Maturín Centro
92
6.4.3 Maturín Oeste
96
6.4.4 Guarico
100
6.5 Hipótesis Local. Entrampamiento de gas
104
6.6 Hipótesis Epirogénica
105
6.7 Hipótesis Regional. Fuente de Calor Cortical
106
CAPITULO 7: CONCLUSIONES Y RECOMENDACIONES
108
REFERENCIAS
111
vii
Figura 1.1: Localización del área de estudio
3
Figura 2.1: Maneras de Transportar calor
8
Tabla 2.1: : Concentraciones típicas de los elementos radioactivos y producción de calor de
11
algunos tipos de rocas
Figura 2.2: Geotermas de la Litosfera
14
Figura 3.1: Fundamento del modelo de extensión litosférica
20
Figura 3.2: Cuenca extensiva o tipo graben (modelo de extensión litosférica)
21
Figura 3.3a: Cuencas antepaís o “foreland”
23
Figura 3.3b: Cuenca ante-arco o “fore-arc”
23
Tabla 3.1: Conductividades termales publicadas por diferentes autores
25
Figura 3.4: Valores típicos de Flujo de Calor asociado a diferentes tipos de cuencas
39
Sedimentarias
Figura 3.5: Diagrama Esquemático del proceso de Descompactación o Backstripping.
31
Figura 3.6: Diagrama esquemático de una columna sedimentaria reconstruida (con carga) y
35
una columna sedimentaria descompactada (sin carga)
Figura 3.7: Modelos de Airy y Pratt
39
Figura 4.1: Situación limítrofe actual del Caribe.
40
Figura 4.2: Reconstrucción palinspática del Caribe en el Jurásico Temprano
44
Figura 4.3: Reconstrucción palinspática del Caribe en el Aptiense Temprano
45
Figura 4.4: Reconstrucción palinspática del Caribe en el Paleoceno Tardío
45
Figura 4.5: Reconstrucción palinspática del Caribe en el Oligoceno Temprano
46
Figura 4.6: Reconstrucción palinspática del Caribe en el Mioceno Tardío
46
Figura 4.7: Mapa de Ubicación de la Cuenca Oriental de Venezuela
48
Figura 4.8: Cortes geológicos Subcuenca de Guárico
50
Figura 4.9: Columna Estratigráfica de la Cuenca Oriental de Venezuela
53
Figura 4.10: Migración del frente de Deformación del Caribe hacia el este-suroeste en el
55
norte de Venezuela
Figura 4.11: Esquema evolutivo de la Subcuenca de Guarico
60
Figura 4.12: Mapa geológico esquemático y cross-secciones del Sistema Montañoso del
62
Caribe
Figura 4.12: Principales elementos estructurales en la Cuenca Oriental de Venezuela
viii
63
Figura 4.13: Serranía del Interior Oriental y sus fallas más importantes
64
Tabla 5.1: Parámetros de porosidad-profundidad para litologías del Mar del Norte
66
Figura 5.1: Localización del perfil B-3 y los pozos cercanos.
67
Tabla 5.2: Información seleccionada, Maturín Norte
68
Tabla 5.3: Información seleccionada, Maturín Centro
68
Tabla 5.4: Información seleccionada, Maturín Oeste.
69
Tabla 5.5: Información seleccionada, Guarico
69
Figura 5.2: Ubicación de los pozos seleccionados para construir la sección característica de
70
Maturín Centro, Maturín Oeste y Guárico.
Figura 5.3: Secciones Compuestas: (a) Guarico, (b) Maturín Oeste, (c) Maturín Centro y (d)
71
Maturín Norte
Figura 5.4: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, en
73
Maturín Norte
Figura 5.5: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy,
73
Maturín Norte
Figura 5.6: Tasa de Subsidencia vs. Edad, Maturín Norte .
74
Tabla 5.6: Tasas de Subsidencia y sus mecanismos asociado, Maturín Norte
74
Figura 5.7: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, Maturín
75
Centro
Figura 5.8: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy,
75
Maturín Centro
Figura 5.9: Tasa de Subsidencia vs. Edad, Maturín Centro
76
Tabla 5.7: Tasa de Subsidencia y su mecanismo asociado, Maturín Centro
77
Figura 5.10: Profundidad descompactada vs el tiempo de cada unidad estratigráfica,
78
Maturín Oeste
Figura 5.11: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy,
78
Maturín Oeste
Figura 5.12: Tasa de Subsidencia vs. Edad, Maturín Oeste
79
Tabla 5.8: Tasa de Subsidencia y su mecanismo asociado, Maturín Oeste
79
Figura 5.13: Profundidad descompactada vs el tiempo de cada unidad estratigráfica,
81
Guarico
Figura 5.14: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy,
81
Guarico
Figura 5.15: Tasa de Subsidencia vs. Edad, Guarico
ix
82
Tabla 5.9: Tasa de Subsidencia y su mecanismo asociado, Guarico
82
Figura 6.1: Perfil de temperatura compuesto para Maturín Norte
86
Figura 6.2: Perfil de temperatura compuesto para Maturín Centro
86
Figura 6.3: Perfil de temperatura compuesto para Maturín Oeste
87
Figura 6.4: Perfil de temperatura compuesto para Guarico
87
Tabla 6.1: Parámetros y valores característicos generales en la zona de Maturín Norte.
89
Figura 6.5: Geoterma Litosférica Calculada en Maturín Norte
90
Figura 6.6: Curvas Observada y Calculada en Maturín Norte, en sedimentos.
91
Tabla 6.2: Parámetros y valores característicos en Maturín Norte, en sedimentos.
92
Tabla 6.3: Parámetros y valores característicos generales en la zona de Maturín Centro
93
Figura 6.7: Geoterma Litosférica Calculada en Maturín Centro
94
Figura 6.8: Curvas Observada y Calculada en Maturín Centro, en sedimentos.
95
Tabla 6.4: Parámetros y valores característicos en Maturín Centro, en sedimentos.
95
Tabla 6.5: Parámetros y valores característicos generales en la zona de Maturín Oeste
97
Figura 6.9: Geoterma Litosférica Calculada en Maturín Oeste
98
Figura 6.10: Curvas Observada y Calculada en Maturín Oeste, en sedimentos.
99
Tabla 6.6: Parámetros y valores característicos en Maturín Oeste, en sedimentos.
100
Tabla 6.7: Parámetros y valores característicos generales en la zona de Guarico
102
Figura 6.11: Geoterma Litosférica Calculada en Guarico
103
Figura 6.12: Curvas Observada y Calculada en Maturín Oeste, en sedimentos.
104
Tabla 6.8: Parámetros y valores característicos en Guarico, en sedimentos.
104
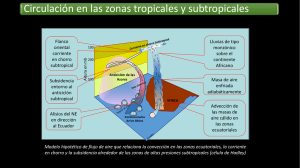
Figura 6.13: Sección Termal de un perfil oeste-este en la subcuenca de Guarico
106
Figura 6.14: Flujo de Calor para Venezuela
107
x
1
La Cuenca Oriental de Venezuela se subdivide en dos subcuencas: la de Guárico y la de Maturín,
ubicadas al oeste y este, respectivamente. Movimientos tectónicos ocurridos durante el Eoceno-Plioceno
fueron los responsables de esta separación. El Arco de Urica es el principal elemento estructural que
separa las subcuencas de Maturín y de Guarico. La Cuenca Oriental se encuentra limitada al norte por la
Serranía Interior Central y Oriental, al sur por el escudo de Guayana, al este por el Delta del Orinoco, y al
oeste por el lineamiento del Baúl. Tiene una orientación este-oeste, con unos 800 km de largo y 200 km
de ancho, lo que representa una superficie de aproximadamente 165.000 km2 (González de Juana, 1980).
El presente trabajo de grado pretende continuar el estudio de Fernández (2004), “Análisis Termal
de la Cuenca Oriental de Venezuela”, el cual reveló que hacia el noreste de la Subcuenca de Guárico
existe una zona donde a una profundidad de aproximadamente 2000 m, se registran temperaturas
anómalas de 420ºK (ó 146.85 ºC). Por tal motivo se hace necesario realizar un modelado termal que
integre datos sísmicos y de pozos (temperaturas y litologías) en cuatros regiones representativas de la
Cuenca Oriental; Guarico, Norte, Oeste y Centro de Maturín, para finalmente establecer un marco termal
consistente con la información disponible del área en estudio.
A través del modelado termal 1D se puede reconstruir la distribución de temperaturas y de flujo
de calor de una cuenca sedimentaria actual través del tiempo geológico, aunque este trabajo solo
reproduce el comportamiento
termal actual. Además es posible relacionar el estado termal con los
distintos procesos de subsidencia ocurridos en la misma, lo que contribuye significativamente para
determinar muchos procesos internos de la cuenca dependientes de la temperaturas como: maduración
de hidrocarburos, migración de fluidos y reacciones diagenéticas.
1
2
Generar modelos termales (1D ) en cuatro regiones representativas de la Cuenca Oriental de
Venezuela (Norte de la subcuenca de Guarico, Norte, Centro y Oeste de la subcuenca de Maturín), que
logren explicar el comportamiento termal del área y la existencia de la anomalía térmica hacia el oeste de
la cuenca.
Recopilar información bibliográfica sobre la evolución termal, isostasia y flexura de cuencas
sedimentarias antepaís y de extensión en el mundo, para analizar y reconciliar los modelos
geológicos planteados de la Cuenca Oriental de Venezuela.
Aplicar rutinas de “backstripping” o retro-evolución para calcular el espesor de la capa de
sedimentos a través del tiempo geológico, y así cuantificar la subsidencia total producida
en la Cuenca Oriental por efectos por carga sedimentaria, termales y/o tectónicos, la cual
será expresada en curvas de subsidencia.
Calcular tasas de subsidencia con los espesores compactados y descompactados, para
compararlos e identificar las máximas tasas, ocurridas durante la formación de la cuenca.
3
!
"
#
La zona de estudio se encuentra ubicada en el nororiente de Venezuela, entre los meridianos 67º
y 63º de longitud oeste, y entre los paralelos 8 y 10º de latitud norte. Esta área pertenece a la Cuenca
Oriental de Venezuela, la cual limita al norte con la Serranía del Interior Central y Oriental, al sur con el
río Orinoco, al este con el océano Atlántico y al oeste con macizo del Baúl.
CUENCA ORIENTAL
Escudo de
Guayana
Colombia
GUARICO
MATURIN OESTE
MATURÍN CENTRO
MATURÍN NORTE
Figura 1.1: Mapa de localización del área de estudio
4
$
%
1) Revisión bibliográfica.
2) Empleo del paquete de computación GMT 4.0 para la generación de mapas de ubicación del área de
estudio y topografía.
3) Estimación de valores de porosidad en función de la profundidad, en base al estudio previo de Sclater
y Christie (1980).
4) Aplicación de técnicas de retro-evolución (backstripping), tomando en cuenta valores de porosidad
anteriormente estimados.
5) Obtención de curvas de subsidencia, i.e, profundidad del basamento en función del tiempo
6) Cuantificación de las tasas de subsidencia de las unidades compactadas y descompactadas.
7) Modificación del algoritmo FDTHERM, para ser utilizado en 1D
8) Estimación de valores de conductividad termal, producción de calor, densidades, calor especifico y
velocidades de fluidos.
9) Aplicación de algoritmo computacional para generar posibles modelos termales 1D en cuatro
representativas de la Cuenca Oriental.
10) Interpretación regional tectónica y termal de los resultados obtenidos
5
La Cuenca Oriental ha sido objeto de varios estudios de interpretación sísmica, gravimétrica,
magnética, tectónica y evolución termal:
La presencia de gradientes altos de temperatura al norte de la Cuenca Oriental de Venezuela y
su vínculo a un entrampamiento de gas fue propuesto por Urbani (1991). En especial en la Subcuenca de
Guárico, cerca del frente de montañas, hay una serie de campos donde las empresas petroleras han
encontrado grandes yacimientos de gas, estos tipos de yacimientos posiblemente según Urbani (1991)
se deban al proceso compresivo de norte a sur, ya que por el efecto de compresión adiabática de los
fluidos se eleva la temperatura en una franja paralela al frente de montañas, produciendo gran aumento
del gradiente geotérmico de la región (7 ºC/100m).
Márquez (2003) realizó un estudio de la Subcuenca de Guarico, donde logra integrar varias
disciplinas geofísicas, con la finalidad de comprender al máximo el complejo proceso de
evolución
tectónica y termal del área de estudio. Este estudio consistió en el análisis de datos potenciales, sísmicos
y de pozos, con el objetivo de definir un marco tectono-termal consistente con el registro estratigráfico.
Para ello aplicaron rutinas de retro-evolución (backstrippping), modelado de soterramiento y modelado
gravimétrico-magnético. Los resultados del estudio indican que desde el Mesozoico hasta el presente se
han registrados dos episodios de calentamiento continental. El primero de efecto regional, marcando la
extensión del Jurásico Temprano con un pico de flujo de calor de 114 mW/m2 aproximadamente y que
está asociado al crecimiento del Graben de Espino. El segundo se registra a partir del Plioceno y se
interpreta como un episodio incipiente de adelgazamiento cortical, en el NE del Graben de Espino cerca
de Zaraza, con un flujo de calor estimado en 97.1 mW/m2. Se considera que esta anomalía termal es en
parte la causante del levantamiento del frente de montañas de Guárico.
6
Fernández (2004), con base a información de 5 transectos sísmicos, de temperatura de fondo de
pozo y de profundidades de topes geológicos para 57 pozos distribuidos en la Cuenca Oriental de
Venezuela elaboró secciones termales para la zona norte del área, que indican la presencia de un alto
flujo de calor para la región norte de la Subcuenca de Guárico y para las cercanías de la Subcuenca de
Maturín, donde los valores asociados son de 60 a 100 mW/m2. Sin embargo, los valores disminuyen a
medida que se aumenta en profundidad hacia el Este de la Subcuenca. Este estudio sirvió de base para
el Modelado Termal 1D de la Cuenca Oriental de Venezuela que se presenta en este trabajo
Pérez de Armas (2005), realizó un análisis estructural, interpretación de líneas sísmicas de
reflexión y análisis de trazas de fisión de apatito en la Serranía del Interior Oriental y en la subcuenca de
Guarico, este estudio indico que el área experimento una deformación Mesozoica y Terciaria hasta el
Reciente. Además las edades de enfriamiento derivadas del análisis de trazas de fisión de Apatito
sugirieron que la obducción del cinturón de corrimiento del área de estudio ocurrió en el Oligoceno tardío
hasta el Mioceno medio. Datos de campo e interpretación sísmica revelaron también que la deformación
comenzó durante el Eoceno (54 Ma). El resultado más sorprendente en este estudio fue que las edades
adquiridas en las rocas sedimentarias de la parte más oriental del cinturón de corrimiento indican un
evento termal Eoceno, este evento puede estar relacionado con la convergencia NO-SE eocena de las
Placas Norteamérica y Suramericana, que debe haber causado un acortamiento de la litosfera del Proto–
Caribe.
Los trabajos publicados recientemente a cerca del comportamiento o evolución termal de la
Cuenca Oriental de Venezuela, específicamente la subcuenca de Guarico, se han centrado básicamente
en analizar la relación existente entre los altos valores temperatura registrados en esa zona, el aporte de
sedimentos, la compactación, la subsidencia, la maduración térmica y la geodinámica del área. El
presente trabajo busca de alguna manera apoyar, reconciliar o descartar algunos de las hipótesis
aportadas por los trabajos descritos, a través de la aplicación de algoritmos computaciones previamente
probados.
7
&$
&
#
La temperatura generalmente incrementa con la profundidad en la Tierra, esto es la causa
principal de: la maduración de hidrocarburos, metamorfismo termal, varias formas de mineralización y
por supuesto volcanismo, además de otras actividades ígneas. A una cierta profundidad, las rocas están
lo suficientemente calientes para fracturarse y deformarse dúctilmente, mientras que a profundidades
mayores ellas están tan calientes que fluyen como un líquido viscoso (Musset & Khan, 2000).
Para entender la evolución termal de una cuenca sedimentaria cualquiera hay que conocer
algunos conceptos básicos relacionados con el flujo de calor terrestre, por lo que a continuación se
presentan algunos de ellos:
2.1.1 Temperatura – uno de los siete parámetros físicos fundamentales – es una medida cuantitativa del
grado de calor o frío de un objeto relativo a alguna medida estándar (Lowrie, 1997). La temperatura
interna terrestre incrementa con la profundidad, el promedio de este incremento es conocido como
gradiente de temperatura, y es medido en perforaciones en tierra, en condiciones normales oscila entre
25º y 30ºC por kilómetro. Sin embargo, este valor no se mantiene a grandes profundidades, por ejemplo a
más de 100km la temperatura podría ser mayor a 2500ºC, pero por información sismológica sabemos
que el interior de la Tierra es sólido, por lo tanto el gradiente de temperatura debe decrecer con la
profundidad a una escala regional, en parte esto se debe a que el calor viaja con mayor facilidad a mayor
profundidad, a continuación discutiremos de que manera viaja el calor (Musset & Khan, 2000).
2.1.2 Transferencia de Calor
La transferencia de calor entre una región y otra del sistema o bien entre el sistema y sus
alrededores puede llevarse a cabo por tres maneras diferentes: convección, conducción y radiación.
7
8
Conducción es la transferencia de calor a través de un material por interacción atómica o
molecular dentro del material (Figura 2.1a), (Fowler, 1990). En convección la transferencia de calor
ocurre debido a que las moléculas por sí mismas son capaces de moverse de un lugar a otro dentro del
material (Figura 2.1b), (Fowler, 1990). La frecuentemente llamada convección termal se debe a la
combinación de la base caliente y el tope frío, y el calor como en el proceso de conducción, se mueve de
lugares calientes a fríos. La convección es sólo posible en un fluido, mientras que la conducción ocurre
tanto en fluidos como en sólidos (Musset & Khan, 2000). La convección transfiriere calor más rápido que
la conducción (Fowler, 1990).
Frío
Frío
Frío
Caliente
Caliente
Caliente
(b)
(c)
(a)
Figura 2.1: Maneras en que se transporta el calor : (a) Conducción, (b) Convección, (c) Radiación.
Modificado de Musset & Khan, 2000.
La advección es una forma especial de la convección. El término advección se refiere al
transporte de algo de una región a otra. Si una región caliente es levantada por eventos tectónicos,
rebote isostático o erosión, el calor (conocido como calor advectivo) es físicamente levantado con las
rocas (Fowler, 1990).
La Tierra puede ser dividida en una capa fría, bastante rígida -litosfera – que descansa sobre la
caliente astenosfera, que fluye por arrastre. Aunque la astenosfera es extremadamente viscosa, el calor
es transportado dentro de ésta principalmente por convección, pero debido a la rigidez de la litosfera,
esta transporta el calor por conducción. Por lo tanto, el calor originado en el interior de la Tierra sube por
9
convección hasta que alcanza la litosfera, y a partir de aquí continúa viajando hasta la superficie por
conducción (Musset & Khan, 2000).
Convección ocurre localmente en partes de la litosfera. Esto puede ser atribuido al levantamiento
del magma, debido a que está caliente y menos densa, bien sea por la presencia de diapiros y plumas, o
por el movimiento de las placas tectónicas. Convección termal ocurre en aguas subterráneas cuando
estas son calentadas por una intrusión caliente, dando como resultado una circulación hidrotermal, la cual
puede producir mineralización (Musset & Khan, 2000).
El calor también puede viajar por radiación termal, la cual es relacionada a la luz, ondas de radio
y otros tipos de radiación electromagnética. La radiación presenta una diferencia fundamental respecto a
la conducción y la convección: las sustancias que intercambian calor no tienen que estar en contacto,
sino que pueden estar separadas por un vacío.
2.1.3 Geoterma es el perfil de temperatura a través de la Tierra y varía con la profundidad o el tiempo,
ver Figura 2.2. (Musset & Khan, 2000).
2.1.4 Flujo de Calor es la potencia o energía con el cual el calor sube hacia la superficie terrestre, Q, y
es medido en Watts(Joule/seg). El flujo que sube por unidad de metro cuadrado es el flujo de calor, q, y
es medido en W/m2. Debido a que el flujo de calor es calculado usando las ecuaciones de calor de
conducción, este solo incluye calor conducido e ignora cualquier calor de convección en la superficie, el
cual algunas veces será significante (Musset & Khan, 2000).
La relación para el transporte de calor conductivo se conoce como Ley de Fourier, la cual
establece que el flujo de calor q, por unidad de área y por unidad de tiempo en un punto es directamente
proporcional al gradiente de temperatura en ese punto (Fowler, 1990). En una dimensión la Ley de
Fourier es:
10
q = −k
∂T
∂z
( ec. 2.1)
Donde k es la conductividad termal, y z es la coordenada en la dirección de la variación de
temperatura (Fowler, 1990). La conductividad termal es una propiedad física del material, y mide la
habilidad física para conducir calor (Turcotte y Schubert, 2002).
El signo menos que aparece en la ecuación (1) indica que el flujo de calor va en sentido contrario
a la dirección del gradiente de temperatura (Fowler, 1990).
Como los valores de flujo de calor son pequeños, ellos están dados en mW/m2, y oscilan entre 40
a 200 mW/m2. El flujo de calor varía entre dos sitios principalmente debido a cambios de espesor de la
litosfera y a variaciones de la concentración de elementos radioactivos en está. El flujo de calor también
es afectado por procesos orogénicos, intrusiones, erosión, depositación y deformación de la corteza
(Musset & Khan, 2000).
2.1.5 Consideraciones Termales de la Litosfera Oceánica
La litosfera oceánica contiene pequeñas cantidades de elementos radioactivos, así que el flujo de
calor es principalmente debido a calor conducido desde el manto hasta arriba. Sin embargo, el flujo de
calor varía porque el espesor no es constante. La litosfera oceánica esta compuesta principalmente por
rocas basálticas en la corteza (pocos kilómetros) y por debajo se encuentran rocas ultrabásicas del
manto, y ambos tipos de rocas contienen una baja radioactividad (Tabla 2.1) (Musset & Khan, 2000).
La base de la litosfera oceánica es donde la temperatura esta bastante alta por convección y es
aproximadamente la misma en cualquier lado, alrededor de los 1300ºC. Como en el piso oceánico la
temperatura es cercana a los 0ºC, la diferencia entre la base y la superficie de la litosfera oceánica es
11
aproximadamente constante, así que tanto el gradiente de temperatura como el flujo de calor decrece
cuando el espesor incrementa (Musset & Khan, 2000).
GRANITO
BASALTO
THOLELÍTICO
BASALTO
ALCALINO
PERIDIOTITA
Promedio
Corteza Continental
superior
Promedio
Corteza
Oceánica
Manto
Enriquecido
U (ppm)
4
0.1
0.8
0.006
1.6
0.9
0.02
Th(ppm)
15
0.4
2.5
0.04
5.8
2.7
0.1
K(%)
3.5
0.2
1.2
0.01
2.0
0.4
0.02
U
3.9
0.1
0.8
0.006
1.6
0.9
0.02
Th
4.1
0.1
0.7
0.001
1.6
0.7
0.03
K
1.3
0.1
0.4
0.004
0.7
0.1
0.007
Total
9.3
0.3
1.9
0.02
3.9
1.7
0.057
Densidad (kg/m3 )
2.7
2.8
2.7
3.2
2.7
2.9
3.2
Producción de calor (µ W/m3 )
2.5
0.08
0.5
0.006
1.0
0.5
0.02
Concentración por peso
Producción de calor(10-10 W/kg)
Tabla 2.1: Concentraciones típicas de los elementos radioactivos y producción de calor de algunos tipos de rocas.
Modificado de Fowler, 1990.
2.1.6 Consideraciones Termales de la Litosfera Continental y la Radioactividad
El calor radioactivo es la principal fuente de calor interno para la Tierra como un todo; sin
embargo, fuentes de calor local y sumideros aumentan el calor inactivo, al igual que el calentamiento por
cizalla y reacciones químicas endotérmicas (absorben energía o calor) y exotérmicas (liberan energía o
calor) (Fowler, 1990).
En la corteza continental y en la litosfera los procesos termales dominantes son la producción de
calor radiogénico y el transporte de calor conductivo para la superficie. Debido a la gran edad de la
12
litosfera continental, los efectos dependientes del tiempo pueden ser, en general, ignorados (Turcotte
and Schubert, 2002).
La producción de calor media por unidad de masa H esta dada por:
H=
Q
M
(ec. 2.2)
Donde Q (calor) es medido en Watts y M (masa) es medida en kg.
Los principales elementos radioactivos son concentrados en los magmas, particularmente en los
ricos en silicio, y estos tienen una densidad menor que las rocas que son derivadas de ellos, por lo que
tienden a subir a la superficie, donde ellas son intruídas o extruídas en altos niveles de la corteza (Musset
& Khan, 2000).
Generalmente en áreas continentales superficiales las rocas presentan grandes cantidades de
elementos radioactivos, mucho más que las rocas que conforman la corteza oceánica, y la concentración
de estos elementos decrece con la profundidad en la corteza continental (Turcotte and Schubert, 2002).
En áreas específicas existe una relación lineal entre el flujo de calor superficial y la generación o
producción de calor radioactivo superficial. Usando esta relación lineal, se puede estimar
aproximadamente la contribución de los elementos generados en la corteza continental en la superficie
(Turcotte and Schubert, 2002).
La producción de calor debido a elementos radioactivos decrece exponencialmente con la
profundidad:
H ( z ) = Ho exp(− z / D )
(ec. 2.3)
13
Por lo tanto Ho es la producción de calor radiogénico promedio por unidad de masa (W/ kg) en la
superficie (z=0), D es una escala de longitud para la disminución de H con la profundidad (Turcotte and
Schubert, 2002).
Figura 2.1.2: Geotermas de la Litosfera. Tomado de Soto, 2000.
14
&&$
$'
$
La ecuación de transporte de calor es aplicable a numerosos e importantes procesos geológicos,
como por ejemplo, procesos metamórficos, hidrológicos, termales y en estudios diagéneticos.
Basados en Fowler (1990) los principios del transporte de calor serán expuestos brevemente a
continuación, además se presentará una simple y aproximada solución numérica a la ecuación de
transporte de calor.
El calor por unidad de tiempo entrando a un elemento a través de una cara en la dirección z es
aQ(z), mientras que el calor por unidad de tiempo saliendo de este elemento a través de la cara z+δz,
es aQ(z+δz). Expandiendo Q(z+δz) en serie de Taylor resulta:
q ( z + δz ) = q ( z ) + δz
El término
∂q (δz ) ∂ 2 q
+
+ ......... ( ec. 2.4)
∂z
2 ∂z 2
2
(δz )2 y aquellos de órdenes mayores son muy pequeños y pueden ser ignorados. De
la ec. 2.4 la ganancia neta de calor por unidad de tiempo es el calor entrando a través de la cara z menos
el calor saliente a través de la cara z+δz.
= aq( z ) − aq( z + δz )
= − aδz
∂q
∂z
(ec. 2.5)
(ec. 2.6)
Supongamos que el calor generado en este elemento de volumen en una tasa A por unidad de
volumen por unidad de tiempo. La cantidad total de calor generado por unidad de tiempo es entonces
Aaδz
(ec. 2.7)
15
Combinando la expresión 2.6 y 2.7 resulta la ganancia total en calor por unidad de tiempo para
primer orden en δz como:
Aaδz − aδz
El calor especifico
∂q
∂z
(ec. 2.8)
c p del material del cual el elemento esta compuesto determina el aumento de
temperatura debido a esta ganancia en el calor, el calor especifico es definido como la cantidad de calor
necesaria para incrementar 1kg material por 1ºC. El calor especifico se mide en unidades de W kg-1ºC-1.
Si el material tiene una densidad ρ y un calor especifico c p , y experimento un incremento de
temperatura ∂T en un tiempo ∂t , la tasa con la cual el calor es ganado es:
c p aδzρ
δT
δt
(ec. 2.9)
Igualando las ecuaciones 2.8 y 2.9 se obtiene la tasa a la cual el calor es ganado por unidad de
volumen:
c p aδzρ
δT
∂q
= Aaδz − aδz
δt
∂z
cpρ
(ec. 2.10)
δT
∂q
= A−
δt
∂z
En el caso limite cuando δz, δt → 0 , la ec. 2.10 se convierte en:
cpρ
∂T
∂q
= A−
∂z
∂t
(ec. 2.11)
Usando la ec. 2.1 para q (flujo de calor por unidad de área), tenemos que:
16
cpρ
∂T
∂ 2T
= A+k 2
∂t
∂z
(ec. 2.12)
ó
∂T
k ∂ 2T
A
=
+
2
∂t ρc p ∂z
ρc p
(ec. 2.13)
Esta es la ecuación de conducción de calor en una sola dimensión.
En esta ecuación, la temperatura es solo función del tiempo t y de la profundidad z, es decir, no
varía en la dirección x o y. Si se asumiera que la temperatura varía en x, y, z y t, una ecuación de
conducción de calor en tres dimensiones se podría derivar de la misma forma que la ecuación en una
sola dimensión. En sistema de coordenada cartesiano en tres dimensiones resulta:
∂T
k ∂ 2T ∂ 2T ∂ 2T
A
=
+ 2 + 2 +
2
∂t
ρc p ∂x
ρc p
∂y
∂z
(ec. 2.14)
Usando la notación de un operador diferencial, se puede escribir como:
∂T
k
A
=
∇ 2T +
ρc p
ρc p
∂t
(ec. 2.15)
Las ecuaciones 2.14 y 2.15 son ambas conocidas como la ecuación de conducción de calor. El
término k/ρ
c p es conocido como la difusividad termal. La difusividad termal expresa la habilidad de un
material para perder calor por conducción.
Para un estado-fijo donde no hay una variación de la temperatura con el tiempo, se tiene:
∇ 2T = −
A
k
(ec. 2.16)
17
En la ausencia de alguna generación o producción de calor, la ec. 2.16 se convierte en:
∂T
k
=
∇ 2T
∂t
ρc p
(ec. 2.17)
Esta es la ecuación de difusión.
Hasta ahora se ha asumido que no hay un movimiento relativo entre un volumen pequeño del
material y los que están inmediatamente a su alrededor. Ahora considere como la temperatura de un
volumen pequeño cambia con el tiempo si esta en movimiento relativo a través de una región donde la
temperatura varía con la profundidad. Este efecto no había sido previamente considerado, así que la ec.
2.13 y su análogo tridimensional, ec. 2.15, deben ser modificadas. Asumiendo que un volumen se esta
moviendo con una velocidad u en la dirección z, ahora en algún tiempo t, la profundidad será z+ut. El
. ∂T / ∂z ) .El primer término
∂T / ∂t en la ec. 2.13 debe por lo tanto ser remplazado por ∂T / ∂t + (dz / dt )(
es la variación de la temperatura con el tiempo a una profundidad fija z. El segundo término
(dz / dt )(. ∂T / ∂z ) es igual a u (∂T / ∂z ) y explica el efecto del movimiento de un volumen pequeño del
material a través de una región donde la temperatura varía con la profundidad. Las ecuaciones 2.13 y
2.15 se convierten en, respectivamente,
∂T
k ∂ 2T
A
∂T
=
+
−u
2
∂t
ρc p ∂z
ρc p
∂z
(ec. 2.18)
y
∂T
k
A
=
∇ 2T +
− u.∇T
∂t
ρc p
ρc p
(ec. 2.19)
En la ec. 2.19, u es la velocidad en tres dimensiones de el material. El término u.∇T es el
término de transferencia advectiva, y también se puede expresar como:
18
∂T
k
H
=
∇ 2T +
− u.∇T
∂t
ρc p
cp
(ec. 2.20)
El movimiento relativo entre el volumen pequeño y su alrededor puede ocurrir por varias razones.
La dificulta que involucra la resolución de la ec. 2.18 y 2.19 depende de la causa de este movimiento
relativo. Si el material esta comenzando a erosionarse o a depositarse justo sobre el pequeño volumen
considerado anteriormente, entonces el volumen esta comenzando a alejarse o acercarse más hacia la
superficie fría de la Tierra. En este caso u, es la tasa en la cual la erosión o depositación toman lugar.
Este es el proceso de advección referido anteriormente. Por otra parte, el elemento de volumen puede
formar parte de una celda de convección termal impulsada por diferencias de densidades temperaturainducida. En este último caso, el valor de u depende del mismo campo de temperatura y de otros factores
externos, tal como tasas de erosión. El hecho que, para convección, u es una función de la temperatura
hace que la ecuaciones 2.18 y 2.19 sean no lineales y significantemente más difíciles de resolver.
19
:
La evolución de las cuencas sedimentarias es afectada o condicionada por movimientos
verticales de la corteza o mejor conocidos movimientos epirogénicos. Aunque el ambiente tectónico
puede variar durante su evolución, ellas se pueden clasificar en cuatro grupos según la tectónica: las
ubicadas en regímenes extensivos, las asociadas a regímenes compresivos, cuencas cratónicas y
cuencas de ambientes tectónicos transcurrentes (Miall, 1984; Mackenzie,1978). En este trabajo solo se
consideraran las primeras dos cuencas mencionadas, ya que el área en estudio solo es afectada por
procesos extensivos y compresivos.
3.1.1 Cuencas en regímenes extensivos
En este grupo se encuentran las cuencas de márgenes pasivos y las cuencas cratónicas. Debido
a que varios autores han estudiado este tipo de cuencas, entre los cuales se puede mencionar: Sleep
(1971), Falvey (1974), Mackenzie (1978) y Sawyer et.al (1987) entre otros, se han propuesto algunos
modelos conceptuales y mecanismos de formación y evolución. A continuación se explicara el modelo de
Mckenzie (1978), ya que es uno de los más aceptados.
3.1.1.1 Modelo de extensión litosférica
El mecanismo generador de la subsidencia es la extensión de la litosfera sobre una región
considerablemente amplia. La magnitud de la extensión según este autor podría ser expresada mediante
un factor β uniforme (Figura 3.1). La fase inicial de estiramiento debería estar acompañada de fallamiento
y compensación isostática, generando así una subsidencia inicial, lo que ocasiona un incremento del
gradiente geotérmico. El decaimiento del gradiente termal con el tiempo genera subsidencia, la cual es
amplificada por el peso de los sedimentos. La cuenca resultante es simétrica (Mckenzie, 1978).
19
20
:
La primera consecuencia de esta extensión sería el adelgazamiento de la litosfera, además del
ascenso pasivo de la astenósfera caliente, ver Figura 3.2. Así mismo se produciría una perturbación
térmica que luego decaería gradualmente con el tiempo explicando la subsidencia de tipo exponencial
observada en las cuencas de regímenes extensivos. Durante esta etapa de subsidencia, el peso de los
sedimentos y de la columna de agua serían factores que aumentarían la magnitud de la subsidencia
termal (Márquez 2003).
Figura 3.1: Fundamento del modelo de extensión litosférica. En el tiempo t = 0 la litósfera continental (Lo y tc) de espesor “a” es
extendida y adelgazada en un factor(β). Se produce una subsidencia inicial por ajuste isostático y el ascenso de la astenósfera
caliente (A) ocasiona un incremento del gradiente geotérmico. El decaimiento del gradiente termal con el tiempo genera
subsidencia, la cual es amplificada por el peso de los sedimentos.
21
:
Steckler y Watts (1978) utilizaron la técnica de “backstripping” para examinar el origen de la
subsidencia del margen continental tipo Atlántico de New York (Estados Unidos). La forma de la curva de
subsidencia tectónica fue interpretada en términos de un modelo termal simple,
enfriamiento de la
litosfera por extensión. Basados en este modelo estimaron la subsidencia total y el adelgazamiento
cortical en este margen, esto sirvió de apoyo para el modelo de extensión litosférica.
Figura 3.2: Cuenca extensiva o tipo graben (modelo de extensión litosférica). Modificado de Earle, 2004.
!
"!# $%"
En este grupo se incluyen la cuencas tipo “foreland” o antepaís (Figura 3.3a),
ante-arco o
“forearc” (Allen y Allen ,1990), Figura 3.3b.
Beaumount (1981) postuló que el peso del orogéno en movimiento causa una flexura litosférica y
de este modo se genera el espacio suficiente para la recepción de los sedimentos, los cuales amplifican
el efecto de subsidencia primaria.
Eventualmente el espacio se rellenaría completamente de sedimentos, generando así más
subsidencia y el levantamiento periférico correspondiente sería eliminado por la erosión. De ser cierto
esto, el análisis se realizaría tomando en cuenta que las cargas pueden adicionarse simultáneamente o
por etapas, siendo a su vez reducidas por erosión.
22
:
El término Cuenca Antepaís se ha aplicado a las cuencas sedimentarias formadas entre las
cadenas montañosas y el cratón adyacente (Dickinson, 1974). Dichas cuencas se han interpretado como
la consecuencia de la respuesta elástica de la litósfera (flexión o compensación regional) frente a la carga
producida por el emplazamiento de mantos de corrimiento (García, 1998). Esta interpretación se ha
basado en el hecho de que estas cuencas están típicamente flanqueadas por dos márgenes de muy
distintas características: un margen pasivo en el lado cratónico, donde emerge el basamento poco o nada
deformado, y un margen activo constituido por el orógeno, en el que se observa un importante
acortamiento aproximadamente coetáneo con la formación de la cuenca (García, 1998). El hundimiento
progresivo del basamento hacia la cuña orogénica (donde alcanza la máxima profundidad) refleja un
basculamiento relacionado con el emplazamiento de la carga.
Posteriormente Kominz y Bond (1986) desarrollaron un modelo de conducción de calor
unidimensional, para simular los efectos térmicos de la subsidencia en las cuencas “foreland” o antepaís.
Sus resultados arrojaron que la generación de una anomalía termal negativa en la cuenca podría retardar
la maduración de hidrocarburos por unos pocos millones de años. La anomalía termal es mas grande
dentro de la litosfera que en los sedimentos. Como la anomalía es removida por el calor conductivo las
propiedades reológicas de la litosfera son modificadas, causando una aparente reducción de la rigidez de
la placa. Esta anomalía termal también da lugar a un levantamiento termal conductivo, cuando cesan los
episodios de carga litosférica.
Un modelo integrado del proceso de transición de cuencas de margen pasivo a cuencas tipo
“foreland” ha sido elaborado por Stolmack (1986), indicando entre otros aspectos que la profundidad
alcanzada por las cuencas “foreland” esta fuertemente influenciada por la carga o peso del orogéno en
avance, Márquez (2003).
23
:
a)
b)
Figura 3.3: Cuencas Comprensivas: (a) Tipo “Foreland” o antepaís, (b)Tipo “Fore-arc” o ante-arco.
Modificado de Earle, 2004.
24
:
Existen varios factores internos que influyen en la distribución de temperaturas dentro de las
cuencas sedimentarias, como: 1) Variaciones en la conductividad termal, 2) Producción o generación de
calor interno, y 3) Transferencia de calor convectivo/advectivo dentro de los sedimentos, (Allen & Allen,
1990).
3.2.1 Efecto de la conductividad termal
La distribución de temperatura con la profundidad (geoterma) en los continentes es determinada
por el transporte de calor conductivo. En el capítulo anterior se dió a conocer la relación entre el flujo de
calor y el gradiente de temperatura según la Ley de Fourier, ec. 2.1. Esta ley establece que el flujo de
calor conductivo esta relacionado con el gradiente de temperatura por un coeficiente, k, conocido como el
coeficiente de conductividad termal (Allen y Allen, 1990).
Ignorando por el momento las variaciones litológicas, la conductividad termal de los sedimentos
varía en función de la profundidad debido a la pérdida o disminución de su porosidad con la profundidad
(Allen y Allen, 1990).
La conductividad termal puede ser estimada si la litología y el fluido de poro es conocida. La
conductividad termal depende de la estructura mineralógica (cuarzo, feldespato, calcio, carbonato, etc), el
tipo y cantidad granos finos en la matriz (usualmente arcillas minerales), y el tipo y volumen del fluido de
poro (usualmente agua). La estructura de la conductividad termal individual, matriz y fluido de poro son
también dependiente de la temperatura. La conductividad termal efectiva es casi invariante con la
profundidad. Esto es porque la disminución de la conductividad de los granos de cuarzo debido al
aumento de temperatura compensa los efectos de la compactación, que aumentan conductividad (Allen y
Allen, 1990).
25
:
Feldespatos y ciertas arcillas no muestran un efecto tan marcado de la temperatura en la
conductividad termal, así que el efecto de compactación podría dominar. En mezclas de agua y arcilla
(lutitas) la conductividad aumenta rápidamente con la profundidad, por la compactación, mientras que un
feldespatos mezclado con agua, la conductividad aumenta más lentamente con la profundidad, debido a
que esta mezcla compacta de manera muy similar a la arena (Allen y Allen, 1990).
Diferentes autores (Beardsmore,1996; Majorowicz y Jessop, 1981; Beach et al., 1987;
Razujevic,1976; Reiter y Jessop, 1985; Taylor et al., 1986; Roy et al.,1981; Reiter y Tovar, 1982;
Toulukian et al.,1970; Drury, 1986; Barker, 1996) han publicado valores típicos de conductividad termal
para las litologías más comunes.
FUENTES
Litología
Arenisca
Caliza
Lodolita
Dolomita
Lutita
Glauconita
Halita
Aftanita
Cuarcita
Granito
Basalto
Toba
Conglomerado
Carbon
Sedimento
Típico
7,1
2,9
2,9
3,1
2,9
4,2+1,4
2,9
3,1+1,3
2,4+0,9
5,0+0,6
1,5+0,5
3,1+1,4
1,4+04
3,2
5,5+1,8
3,7+1,2
2
2,8
4,7+0,8
3,7+1,2
4,8+1,5
2,1+0,4
1,4
4,7+2,8
1,8
1,9+0,4
3,7+1,8
2,0+0,4
4,7+1,1
2,1+0,4
1,8+0,3
4,2+1,5
6
1,8
3,2+0,8
3,2
0,3+0,1
0,2+0,2
3,5+0,4
5,6+1,9
3,4+1,2
3,5+0,4
2,8+0,6
1,7
2,4+0,9
2,0+0,2
1,5
1,7+0,3
1,7+0,6
0,2+0,04
5,0+2,4
0,2+0,1
5,9+0,8
0,3+0,1
2,3+2,0
Conductividad en W/mK
* Valores de la matriz de conductividad, sólo representa la conductividad del volumen cuando la porosidad = 0
Fuentes: 1 = Beardsmore (1996), 2 = Majorowicz y Jessop (1981); 3 = Beach, Jones y Majorowicz (1987); 4 = Razujevic (1976);
5 = Reiter y Jessop (1985); 6 = Taylor, Judge y Allen (1986); 7 = Roy et al. (1981); 8 = Reiter y Tovar (1982)
9 = Touloukian et al. (1970b); 10 = Drury (1986); 11 = Barker (1996).
Tabla 3.1: Conductividades termales publicadas por varios autores. Modificado de Beardsmore y Cull, 2001.
3.2.2 Efectos de la Producción de Calor interno en los sedimentos
Generación de calor por decaimiento radioactivo en sedimentos puede afectar significativamente
el flujo de calor en cuencas sedimentarias (Rybach, 1986). Aunque todos los isótopos radioactivos
generan calor naturalmente, la única contribución significante viene de la serie de uranio y torio y de
40
K.
Consecuentemente, la producción de calor varía con la litología, siendo generalmente más baja en
26
:
evaporitas y carbonatos, baja a media en arenas, alta en lutitas y limolitas, y muy alta en lutitas negras
(Rybach, 1976; Haack, 1982; Rybach y Cermak, 1982).
En continentes, la radioactividad cortical puede explicar una proporción grande (20-60 por ciento)
del flujo de calor superficial (Allen y Allen, 1990).
Para un flujo de calor puramente convectivo, en una dimensión (vertical), la producción de calor
puede ser estimada a partir de registros Gamma-Ray. El efecto de la producción de calor interno es
mayor a grande profundidades. La temperatura aumenta después de un tiempo t, por la producción o
generación de calor interno, pero el cambio de temperatura neto también depende de la tasa de perdida
de calor conductivo. En tiempo geológico mayor 10 Ma el incremento de temperatura puede ser
considerable (Rybach, 1986). Generación de calor interno por lo tanto puede afectar fuertemente el
campo de temperatura en la cuenca si esta tiene una profundidad mayor a los 5 km o existe hace más de
10Ma (Allen y Allen, 1990).
3.2.3 Efecto de la circulación de agua
La temperatura en cuencas sedimentarias puede también ser afectada por flujo advectivo de
calor a través de acuíferos regionales. Tales procesos pueden causar un flujo de calor superficial
anómalamente bajo en regiones de recarga, y anómalamente alto en regiones de descarga (Allen y
Allen, 1990).
Andrews–Speed et al. (1984) encontraron que las medidas de flujo de calor sugerían fuertemente que
existía circulación de agua a profundidad, posiblemente controlada por la configuración de las fallas, en el
aulacogeno del Mar del Norte. Modelos simples de flujo de calor conductivo 1D predicen pobremente el
actual flujo de calor en las cuencas sedimentarias. La mayoría de las cuencas afectadas fuertemente son
probablemente las cuencas continentales con levantamientos, tales como: cuencas antepaís y algunos
rifts intracratonicos (Allen y Allen, 1990).
27
:
&
'
Robert (1988) sugirió que se puede clasificar las cuencas sedimentarias de acuerdo a historia
paleogeotermal: 1) Cuencas con normal o neo-normal historia paleogeotermal, 2) Cuencas Hipotermales
o más frías que lo normal y 3) Cuencas Hipertermales, más calientes que lo normal.
3.3.1 Márgenes Pasivos antiguos o cuencas con una historia paleogeotermal normal presentan
actualmente gradientes geotermales de 25 a 30ºC/km., por ejemplo; El Congo 27ºC/km, Gabon 25ºC/km,
costa este de los E.E.U.U. del Golfo 25ºC/km, entre otras. Los perfiles de reflectancia de vitrinita muestra
que Ro (Ro es un parámetro óptico, indicador de la madurez de materiales orgánicos presentes en los
sedimentos, no es confiable en niveles bajos de madurez termal, < 0.7 ó 0.8%) esta alrededor de 0.5 por
ciento en una profundidad de 3 km y la forma de la curva es sublineal. La madurez de los márgenes por
lo tanto tienen unos gradientes geotermales normales (Allen y Allen, 1990).
3.3.2 Cuencas Hiportermales incluye fosas oceánicas, cuencas ante-arco y cuencas tipo antepaís.
Fosas oceánicas son frías, con valores de flujos de calor superficiales menores a 1HFU (equivale a
aprox. 40mW/m2 ) , una de la más típica se encuentra en al Archipiélago Japonés (Allen y Allen, 1990).
Las cuencas de tipo “foreland” o antepaís también se caracterizan por presentar bajos gradientes
geotermales, 22ºC/km a 24ºC/km, por ejemplo la Cuenca Antepaís del Norte de los Alpes, en el sur de
Alemania. Estudios en esta zona han revelado que a grandes profundidades, Ro es solo 0.6 por ciento
indicando un bajo gradiente termal para el Terciario, en base a esto se concluyó que bajos gradientes
geotermales actuales en este tipo de cuencas pueden haber sido uniformemente más bajos en el pasado
durante la fase de rápida subsidencia relacionada colisión continental y la flexura (Allen y Allen, 1990).
28
:
La Cuenca Oriental de Venezuela es clasificada como una cuenca tipo foreland o antepaís, pero
según los datos utilizados en este trabajo presenta valores de flujo de calor mayores a 1HFC, los cuales
oscilan entre 3 y 4HFC (Fernández, 2004), por tal motivo esta cuenca se comporta anómalamente en
comparación con otras cuencas antepaís del mundo y con lo predicho en la teoría, ver Figura 3.1.
3.3.3 Cuencas Hipertermales son aquellas encontradas en regiones de extensión litosférica tales como:
cuencas “Backarc”, oceánicas o sistemas de “rifting” continentales, algunas cuencas “strike-slip” y arcos
internos de zonas de subducción de tipo B (Allen y Allen, 1990).
Los “rifts” oceánicos son zonas de un alto flujo de calor, tipicamente de 3 a 4 HFC, aunque
algunos valores ocasionalmente alcanzan los 5 HFC. Algunas cuencas strike slip en California tienen un
alto gradiente geotermal ( 200ºC/km en el Valle Imperial), así que sedimentos muy jóvenes pueden estar
altamente maduros. Rifts continentales tienen el alto flujo de calor hoy día (mayores a 50ºC/km en el Mar
Rojo y por encima de los 100ºC/km en el Valle Superior del Rin) y antiguos rifts continentales tienen una
intensa maduración orgánica en los sedimentos que ellos contienen (Ro entre 2–5 por ciento ) (Allen y
Allen, 1990).
El flujo de calor de Arcos internos son elevados debido a la actividad magmática presente en
esas zonas. La antracitas Terciarias de Honshu, Japón son un ejemplo de esto, presenta valores de Ro
de 2-3 por ciento. Ejemplos similares son encontrados en zonas de colisión oceánicas (i.e., La Cordillera
de los Andes) y zonas de colisión continente-continente (i.e., Los Alpes, al sureste de Francia) (Allen y
Allen, 1990). Los valores típicos de Flujo de Calor de los principales tipos de cuencas sedimentarias son
resumidos en la Figura 3.4.
29
:
mWm-2 q
Figura 3.4 : Valores típicos de Flujo de Calor asociado a diferentes tipos de cuencas sedimentarias.
Modificado de Allen y Allen, 1990
30
:
(
)
*
+ ,
Diversos autores han relacionado la subsidencia tectónica, obtenida por el método de
“backstripping” en cuencas desarrolladas en regímenes extensivos, con curvas que predicen la posición
del basamento a través del tiempo tras la ocurrencia de una anomalía termal regional (Steckler y Watts,
1978; Royden y Sclater, 1980; Bond y Kominz, 1984).
La técnica del “backstripping” consiste en aislar los efectos del peso de las cargas sedimentarias,
paleobatimetría de sedimentación y variaciones eustáticas del nivel del mar, para obtener la profundidad
a la que estaría el basamento sin considerar el peso producido por estos efectos. Esta profundidad
proporciona una medida de las desconocidas “fuerzas tectónicas impulsoras” que son responsables de la
formación de la cuenca y por esta razón se han llamado subsidencia tectónica o levantamiento de la
cuenca. Esta metodología ha sido utilizada por diversos autores para el estudio de las causas de la
subsidencia (Watts y Ryan, 1976; Steckler y Watts ,1978; Bond y Kominz, 1984 y Sawyer et al., 1987).
Para implementar este técnica se necesita conocer las profundidades de una unidad estratigráfica
en el presente, es decir z1 y z2 , tope y base de la unidad o capa, respectivamente, ver Figura 3.5.
Para calcular el espesor de una capa sedimentaria en algún tiempo pasado, es necesario mover
la capa superior utilizando las curvas de porosidad-profundidad, esto es equivalente a la remoción
secuencial de las capas superiores permitiendo así que la capa inferior sea descompactada (Allen y
Allen, 1990).
31
:
Figura 3.5: Diagrama Esquemático del proceso de Descompactación o Backstripping: a) Remoción de (2) y (3), Descompactación
de (1); b) Adición de (2), Compactación parcial de (1): c) Adición de (3), Compactación Parcial de (2) y Compactación Total de (1).
Modificado de Allen & Allen, 1990.
En sedimentos que presentan una presión normal, la curva de porosidad-profundidad se
comporta de manera exponencial (Athy, 1930; Ruby y Hubbert, 1960). Siendo este el caso, la porosidad
en alguna profundidad esta dada por :
φ = φ o e − cz
(ec. 3.1)
donde c es un coeficiente determinado por la pendiente de la curva de porosidad-profundidad, z es la
profundidad y φο es la porosidad en la superficie.
En este estudio se tomaron valores de φο y c
tabulados por Sclater y Christie (1980) para calcular φ (ver capitulo 5).
El volumen total de una unidad sedimentaria (Vt) es el volumen debido al agua presente en los
poros Vw y el volumen de los granos de los sedimentos Vs.
Vt = Vs + Vw
(ec. 3.2)
donde Vt es el volumen total de la capa sedimentaria, Vs es el volumen de los granos de sedimentos y
Vw es el volumen de agua en los poros y esta relacionado con la porosidad de la siguiente manera:
z2
Vw = φ o e −cz dz (ec. 3.3)
z1
32
:
Integrando resulta :
φo
Vw =
c
(e
− cz1
− e −cz2
)
(ec. 3.4)
A partir de las ecuaciones 3.2 y 3.4, consideramos un corte transversal y luego despejamos zs ,
lo que resulta:
z s = z 2 − z1 −
φo
(e
c
− cz1
− e −cz2
)
(ec. 3.5)
En descompactación el volumen de sedimentos permanece constante, solo el volumen de agua
se expande. El peso del agua en una columna sedimentaria entre la profundidades z’1 y z’2 es:
z´w =
φo
c
(e
− cz´1
− e −cz´2
)
(ec. 3.6)
El nuevo espesor descompactado de la capa sedimentaria es la suma del espesor debido a los
granos de sedimentos (ec. 3.8) y el espesor debido al agua, que es:
z´2 − z1 = z s − z w
(ec. 3.7)
el cual se convierte en :
z´1 − z´ 2 = z 2 − z 1 −
φo
c
(e
− cz 1
)
− e − cz 2 +
φo
(e
c
− cz´1
− e −cz´2
)
(ec. 3.8)
Esta es la ecuación general de descompactación a partir de la curva de porosidad-profundidad,
mediante esta ecuación se puede calcular el espesor de una capa sedimentaria en algún tiempo después
de su deposición y nos permite graficar una curva de subsidencia descompactada o total.
Se necesita de un mecanismo inicial para crear una depresión que permita que los sedimentos
sea acumulados y la cuenca se forme. Interrupciones en la sedimentación y cambios en la geometría de
la cuenca con el tiempo deben ser reajustados por el mecanismo inicial o atribuido a causas
sedimentológicas (Nunn y Sleep, 1984). La contracción termal y una fuerza o impulso tectónico pueden
causar una amplificación de la subsidencia y son considerados como mecanismos impulsores. Otros
mecanismos de subsidencia han sido propuestos: cambio de fase o intrusión de material denso a
33
:
profundidad y procesos sublitosféricos. Estos procesos son discutidos en detalle por: Bott, 1979; Sleep,
Nunn y Chou, 1980; Turcotte, 1980.
3.4.1 Carga Sedimentaria
La subsidencia tectónica real es obtenida después de remover de la subsidencia total, los efectos
producidos por la carga sedimentaria, las variaciones en la profundidad del agua y las fluctuaciones
eustáticas del nivel del mar. La influencia de la carga sedimentaria produce un cambio de la porosidad en
función de la profundidad, y puede ser evaluada de la siguiente manera (Allen y Allen, 1990):
φ=
φ o e − cz´ − e − cz´
1
c
2
z´2 − z´1
(ec. 3.9)
De aquí la densidad de bulk de la nueva capa sedimentaria (ρs) depende de la porosidad y
densidad de los granos de sedimentos (ρsg)
ρ s = φ × ρ w + (1 − φ ) × ρ sg
(ec. 3.10)
La densidad de bulk de toda la columna sedimentaria (ρsm) con i capas es :
ρ sm =
φim * ρ w + (1 - φim ) * ρ s g i
i
S
z´i
(ec. 3.11)
donde φim es la porosidad media de la capa i , ρsgi es la densidad de la misma capa, yi es el espesor de la
capa i, y S es el espesor total de la columna corregida por compactación (Allen y Allen, 1990).
El efecto total de los sedimentos puede ser tratado entonces como un problema de balance de
Isostasia Local tipo Airy, en una dimensión. Donde los sedimentos están remplazando una columna de
agua,
34
:
Y =S
ρ m − ρ sm
ρm − ρw
( ec. 3.12)
donde Y es la profundidad del basamento corregida por carga sedimentaria y ρm, ρw, ρsm son la densidad
del manto, del agua y la media de la columna de sedimento, respectivamente, Figura 3.6. También se
puede incorporar las correcciones por paleobatimetría (diferencia del peso entre la superficie
depositacional y el datum regional)
y por las variaciones eustáticas del nivel del mar (variaciones
pasadas del nivel del mar comparada con el nivel actual) para obtener la subsidencia sedimentaria real,
(Bond y Kominz, 1984):
Y =Φ S
ρ m − ρ sm
ρw
− ∆sl
ρm − ρw
ρm − ρw
+ (Wd − ∆sl )
(13)
donde ∆sl es el paleonivel del mar relativo al presente, Wd es la paleoprofundidad del agua, Φ es
una función del basamento igual a la unidad para isostasia de Airy (Allen y Allen, 1990), ver Figura 3.6.
35
:
Figura 3.6: Diagrama esquemático de una columna sedimentaria reconstruida (con carga) y una columna sedimentaria
descompactada (sin carga). Modificado de Steckler y Watts, 1978
3.4.2 Subsidencia Tectónica
Subsidencia tectónica es también llamada “subsidence impulsora” y es diferente del efecto
isostático por carga sedimentaria y el peso del agua. La subsidencia tectónica, como su nombre lo indica,
es producida por fuerzas tectónicas que afectan el comportamiento de la litosfera. El estiramiento o
“stretching” de la litosfera continental en muchas ocasiones da como resultado el reemplazo de la
relativamente ligera litosfera continental por astenosfera mas densa. La litosfera estirada y adelgazada se
hunde, causando la subsidencia tectónica. Estiramiento ocurre en varios tipos de cuencas sedimentarias
incluyendo rifts: aulacogenos, cuencas retroarco y cuencas cratónicas (Allen & Allen, 1990).
La carga tectónica también puede producir subsidencia. El peso adicional de cargas tectónicas
tales como: pliegues y cinturones de corrimientos causan que la litosfera continental se hunda,
36
:
conduciendo a subsidencia tectónica. Debido a que la litosfera continental responde flexuralmente, la
subsidencia ocurre no solo inmediatamente por debajo de la carga, sino también en una ancha región
alrededor de la carga. La carga tectónica es particularmente importante en regiones orogénicas tales
como cuencas antepaís (Allen y Allen, 1990).
La subsidencia tectónica se puede cuantificar removiendo el efecto de la carga sedimentaría de la
subsidencia total, mediante la técnica de “backstripping” o retro-evolución. Es difícil en este sentido
separar cuantitativamente la subsidencia tectónica de la subsidencia termal, ya que ambas están
contenidas dentro de este resto.
3.4.3 Subsidencia Termal
Subsidencia termal decrece exponencialmente con el tiempo. La subsidencia termal es
especialmente importante en márgenes pasivos y en cuencas cratónicas (Allen y Allen, 1990).
Las causas de esta subsidencia incluyen el peso sedimentario, actividad tectónica y la
contracción termal durante el enfriamiento de la litosfera. Las cuencas sedimentarias no son producidas
por sedimentación, pero si por procesos tectónicos y termales. El enfriamiento litosférico en profundidad,
que da lugar a la contracción termal para recuperar el equilibrio isostático, especialmente causa la
subsidencia termal. Cuando la subsidencia tectónica cesa, la subsidencia termal se convierte en la
componente principal que afecta la formación de la cuenca (Renaut y Ashley, 2002).
En la formación de cuenca una región de la corteza es calentada, esto causa expansión, lo cual
conlleva a cambios de densidad. El levantamiento ocurre antes de la erosión, y la erosión reduce el
espesor de la corteza. Como la litosfera se enfría y contrae la cuenca se forma. Básicamente es esta
expansión horizontal y adelgazamiento de la litosfera lo que forma la cuenca. El adelgazamiento de la
litosfera ocurre durante el rifting, después del rifting continúa la subsidencia debido a la contracción termal
de la litosfera. Cuando el rifting comienza existe una gran cantidad de calor acumulado el cual cae
rápidamente a medida que el área se aleja rift. Luego la acumulación de sedimento y el peso del agua
37
:
aceleran la subsidencia. Diferentes condiciones termales y tectónicas en diferentes escenarios
de
tectónicas de placa pueden conducir diferentes tipos de subsidencias y procesos de formación de
subsidencia aunque las causas primarias sean las mismas (Renaut y Ashley, 2002).
En zonas extensionales, el “rifting” es la principal causa de la formación de la cuenca. Como los
rifting ocurre en dorsales en medio del océano se comienzan a formar cuencas oceánicas. Estas cuencas
eventualmente conducen a formación de márgenes pasivos. Esto es conocido como rift y deriva. Se
espera que los márgenes pasivos muestren un negativo termal, enfriamiento exponencial después del
rifting. La formación de un margen pasivo es importante para entender la subsidencia termal, debido a
que la subsidencia termal en zonas extensionales ocurre entre la dorsal y el margen pasivo. La cuenca es
más grande mientras se va alejando de la dorsal, y consigue ser mas ancha mientras se vuelve más
vieja, fría y densa. Esto eventualmente puede conducir a la formación de una zona de subducción a lo
largo del margen (Allen y Allen,1990).
Generalmente en márgenes pasivos puede observarse mayor subsidencia que la que puede ser
explicada por simple adelgazamiento de la corteza y de la litosfera. Usualmente la subsidencia comienza
durante la formación de las dorsales oceánicas, esta es considerada subsidencia tectónica, sin embargo
la subsidencia puede ser causada por la baja densidad de la astenosfera que se extiende por debajo de
la zona de rifting. Una pluma de manto puede brindar material del manto caliente a profundidades
someras, y además tener una viscosidad lo suficientemente alta, por lo que no necesita enfriarse de
manera convectiva por un largo período de tiempo. Por lo tanto, la astenosfera caliente puede
permanecer bajo el rift por millones de años antes de fluir hacia fuera. Para anchos rifts y bajas tasa de
expansión del piso oceánico, la tasa de subsidencia es similar a la subsidencia termal (Hamblin y
Christiansen, 1998).
38
:
Isostasia en geodinámica se refiere al equilibrio de fuerzas que debe existir sobre la capa externa
resistente de la Tierra. Airy (1855) y Pratt (1855) basados en medidas gravimétricas realizadas en los
Andes e Himalaya propusieron los primeros modelos de compensación isostática. Según el principio de
isostasia, existe una cierta profundidad, denominada profundidad de compensación, a partir de la cual la
presión creada por los materiales suprayacentes no varía lateralmente. Es decir, el peso de la columna
de material existente entre un punto cualquiera de la superficie de la Tierra y la profundidad de
compensación es constante en todo el planeta.
Esta hipótesis supone implícitamente la existencia de una capa externa más resistente que
descansa sobre un material fluido que se redistribuye hasta alcanzar el equilibrio hidrostático.
Los modelos de Airy y Pratt (Figura 3.5) son clasificados como modelos de compensación local,
pues suponen que la compensación en cada columna se alcanza sin transmitir esfuerzos a las columnas
adyacentes. Así, cuando se forma un orógeno, el exceso de carga debido a la topografía debería ser
compensado en cada punto con un déficit de masa localizado bajo el mismo punto, en algún lugar por
encima del nivel de compensación. Aunque estos modelos resultan adecuados en algunos casos para
explicar los movimientos verticales de la corteza, la compensación isostática local predice un
comportamiento independiente del tamaño de la carga, lo cual no siempre coincide con las observaciones
(Barrell, 1914; Banks et al., 1977).
La litósfera se comporta como una placa rígida que descansa sobre una capa fluida (astenosfera)
cuando es sometida a fuerzas externas, transmitiendo lateralmente los esfuerzos generados. Este
fenómeno, conocido con el nombre de isostasia regional o flexión, se ha utilizado para explicar la
deformación de la litósfera en regiones muy diversas: montañas volcánicas marinas, zonas de
subducción, cuencas antepaís, deltas, etc. (e. g. Turcotte et al., 1978; Watts et al., 1982; McNutt y
Menard, 1982).
39
:
Figura 3.7: Modelos de Airy y Pratt. El modelo de Pratt asume que el exceso de masa se compensa con variaciones laterales de
densidad mientras que el modelo de Airy plantea que dicho exceso se compensa con la aparición de una raíz debajo de la cadena
montañosa. Tomado de Rondón, 2004.
En general, la flexión de la litósfera puede ser explicada mediante un modelo de placa delgada,
que muestra propiedades coincidentes con las observaciones. Así, por ejemplo, la deflexión es máxima
junto a la carga y disminuye progresivamente al alejarse de ésta. Además, se observa que a cierta
distancia de la carga, la deflexión llega a anularse y cambia de signo, formando una elevación que recibe
el nombre de levantamiento posterior (forebulge) (García, 1998).
40
La Placa Caribe limita al norte con la Placa Norteamericana, al oeste con Centro América, y tanto
al sur como al este con la Placa Suramericana. Los límites occidental y oriental consisten de sistemas
colisionales con arcos magmáticos diferentemente evolucionados (Istmo de América Central, Antillas
Menores, respectivamente) mientras que los límites del norte y sur están representados por importantes
zonas de sutura (Cinturón de Motagua en Guatemala, Antillas Mayores, Sistema Montañoso del norte de
Venezuela) (Giunta et al., 2003).
Figura 4.1: Situación limítrofe actual del Caribe. Las flechas muestran las direcciones de movimiento de
las principales placas (Tomado de Giunta et al., 2003).
40
41
La constitución geológica de la Placa Caribe es oceánica (Diebold et al., 1981). Estudios de
refracción sísmica (i.e., Officer et al., 1959; Edgar et al., 1971; Houtz y Ludwig; 1977, Diebold et al., 1981)
han determinado un espesor para la corteza Caribeña entre 10 a 15km. Este espesor es bastante inusual
(Duncan y Hargraves, 1984), ya que es un poco más gruesa que las típicas cortezas oceánicas del
Pacífico y el Atlántico, por lo que se le considera que es de tipo transicional. Más específicamente, la
corteza típicamente oceánica, posee un espesor promedio de 5 km, pero en las cuencas transicionales
de Venezuela, Colombia y del Golfo de México tienen espesores aproximados de 15, 18 y 20 km,
respectivamente (Ladd y Watkins, 1980). Estas diferencias de espesores han sido atribuidas a que en la
Placa Caribe coexisten cuencas (correspondientes con un suelo oceánico de espesor normal) y “ridges”
que se han visto engrosados por las erupciones volcánicas de basaltos (Houtz y Ludwig, 1977).
El movimiento relativo entre la Placa Caribe y sus vecinas tiene una componente predominante
en dirección E–O aunada a una componente menor en dirección N–S (Pennington, 1981; Sykes et al.,
1982; Schubert, 1988). En la actualidad se ha determinado que la placa Caribe se mueve hacia el este
respecto a Suramérica, a una tasa de aproximadamente 20 mm/año (Weber et a l., 2001)
La historia geológica Cenozoica de la Cuenca Oriental de Venezuela está íntimamente ligada a la
interacción entre la Placa Caribe y la Placa Suramericana, implicando un movimiento y emplazamiento de
bloques alóctonos (Erlich & Barret, 1990; Pindell & Dewey,1991; Di Croce, 1995 y Hung, 1997),
acortamiento y subsidencia de la corteza (Jácome et al., 2003). A continuación se explica la evolución
tectónica tanto de la placa del Caribe como de Venezuela oriental y sus respectivas implicaciones en la
estructura litosférica.
Se han propuesto fundamentalmente dos modelos tectónicos que explican la evolución de la Placa
Caribe:
42
•
Origen in situ: plantea que la placa Caribe se formó hacia el oeste de su actual localización,
pero aún entre Norte y Sudamérica (Meschede y Frisch, 1998).
•
Origen Pacífico: postula que la placa Caribe fue generada en el Pacífico Norte (Placa Farallón) y
migró hacia el este, entre Norteamérica y Sudamérica desde el Cretácico Tardío (Pindell et.
al.,1988; Pindell y Kennan, 2001a).
A continuación se contemplan algunos procesos globales ocurridos desde el Jurásico hasta el
reciente con la finalidad de explicar la formación y desplazamiento de la Placa Caribe, tomando en
cuenta solo la teoría de origen Pacífico.
En el Triásico Superior se da inicio a la ruptura de Pangea. La Placa Suramericana comienza a
separarse de la Placa Africana, esta separación avanza desde el sur hacia el norte en un proceso
diacrónico de “rifting” continental, generando a su vez el margen norte de América del Sur al separar la
Placa de Norteamérica de la de Suramérica al final del Jurásico (Pindell, 1993). La Figura 4.2 muestra
una reconstrucción del oeste de Pangea, en el Jurásico Temprano, no mucho después del comienzo de
la ruptura continental, justo antes del inicio de la formación de corteza oceánica en el Atlántico Central.
Suramérica y África constituyeron una sola placa hasta el Aptiense, y la subsecuente apertura del
Atlántico Ecuatorial aparentemente tuvo poco efecto en la dirección del movimiento relativo entre Norte y
Sudamérica (Pindell et al., 1988; Pindell y Kennan, 200b). En la Figura 4.3 se muestra por primera vez la
región del Caribe dentro del Pacífico.
El desarrollo de sistemas de arcos intra-oceánicos, extendiéndose desde Costa Rica hasta
Ecuador, indica que la placa Caribe se separó de la placa de Farallón en el Aptiense, y desde entonces
se mueve más despacio en sentido NE ó E relativo a Norteamérica. En el Aptiense también se presentó
una inversión en la dirección de subducción entre las Américas, debido a una aceleración de la expansión
43
del Atlántico. Durante el Albiense y el Cretácico Superior el movimiento de placas y la estratigrafía
sugieren el establecimiento de un margen pasivo (Pindell y Kennan, 2001b).
La colisión de la placa Caribe y el arco de islas volcánico de Antillas Holandesas con el
continente Suramericano es diacrónico: en Venezuela ocurrió en el Paleoceno-Eoceno en el occidente,
en el Oligoceno en región nor-central y en el Mioceno en el oriente (Lugo y Mann, 1995).
El margen pasivo culmina en el Paleoceno Temprano en el occidente por el comienzo de la
subducción del proto-Caribe, presentándose una zona de Benioff buzante hacia el sur (Proto-Caribe bajo
Suramérica) (Pindell y Kennan, 2001a; 2001b); la subducción en este transecto acomodó la lenta
convergencia entre Norte y Suramérica. Para el Paleoceno Temprano había comenzado un
levantamiento en el norte de la Serranía como resultado de apoyo flexural de la corteza Suramericana
ante la subducción, Figura 4.4.
La convergencia entre Norte y Sur América comenzó durante el Paleoceno, y en el Eoceno medio
el acortamiento pudo haber sido de aproximadamente 70km (Pindell, 1997), lo cual se manifestó por el
engrosamiento estructural, levantamiento y erosión del margen pasivo (Pindell, 1998). Pindell (1997) y
Pindell et al. (1998) sugieren que esta contracción entre las Placas Norte y Sur Américanas podría haber
deformado la corteza Proto-Caribeña, formando una incipiente zona de subducción.
En el Oligoceno el acercamiento del Caribe, desde el oeste, comienza a afectar los terrenos de
Venezuela Oriental desde el Eoceno Tardío hasta el Oligoceno Temprano (Figura 4.5). Existe un dominio
de colisión oblicua dextral y colisión diacrónica de arco a lo largo del borde norte de Venezuela (Pindell y
Kennan, 2001a). También en el Oligoceno Tardío comienza la fragmentación de la placa de Farallón en
varios bloques, los cuales son actualmente las placas de Nazca, Cocos y Juan de Fuca (Pindell. et al.,
1988).
44
En el Mioceno Temprano continúa la transpresión oblicua entre Caribe y Suramérica; la colisión
en Venezuela se sitúa al este de Maturín (Pindell y Kennan, 2001a). Al nor-oeste del Caribe, una porción
del prisma caribeño había sido cabalgado sobre la Serranía del Interior, conllevando al plegamiento y
cabalgamiento al sur, generando la carga para la cuenca de Maturín.
A finales del Mioceno Medio (hace 12Ma) y continuando en el Mioceno Tardío (Figura 4.6) se
desarrolló un cambio en el azimut del movimiento de la placa del Caribe respecto a las Américas,
pasando de colisión oblicua a una tectónica rumbo-deslizante este-oeste, con un mínimo acortamiento
norte-sur, lo que ha dominado los estilos tectónicos al norte y sur de la región caribeña (Pindell y Kennan,
2001b), manteniendo el Caribe sur-este bajo un régimen transtensional (Pindell y Kennan, 2001a).
Según Sykes et al. (1982) este régimen geodinámico debió mantenerse muy similar durante al
menos los últimos 38Ma para conferirle al Caribe su forma actual (Figura 4.6).
Figura 4.2: Reconstrucción palinspática del Caribe en el Jurásico Temprano. Teoría de origen del Caribe en el Pacífico
Modificado de Pindell y Kennan (2001a).
45
Figura 4.3: Reconstrucción palinspática del Caribe en el Apítense Temprano.
Teoría de origen del Caribe en el Pacífico. Modificado de Pindell y Kennan (2001a).
Figura 4.4: Reconstrucción palinspática del Caribe en el Paleoceno Tardío. Teoría de origen
del Caribe en el Pacífico. Modificado de Pindell y Kennan (2001a).
46
Figura 4.5: Reconstrucción palinspática del Caribe en el Oligoceno Temprano. Teoría de origen
del Caribe en el Pacífico. Modificado de Pindell y Kennan (2001a).
Figura 4.6: Reconstrucción palinspática del Caribe en el Mioceno Tardío. Teoría de origen
del Caribe en el Pacífico. Modificado de Pindell y Kennan (2001a).
47
Abarca un área total de aproximadamente 165.000 km2 y se extiende a través de los estados
Guárico, Anzoategui, Monagas, Delta Amacuro, y parte de Sucre. (CEPET, 1989; Aymard et al., 1990).
Se encuentra localizada entre 8° y 11° de latitud norte y 61° y 66° de longitud oeste (Di Croce, 1999),
Figura 4.7. Sus limites son: al norte la Serranía Interior Central y Oriental , al sur el Río Orinoco, al este la
Plataforma del Delta del Río Orinoco y al oeste por el levantamiento del Baúl (Yoris y Ostos, 1997).
Comprende la subcuenca de Guárico al oeste y la subcuenca de Maturín al este, separadas por el Arco
de Úrica hacia el sur ambas sub-cuencas están separadas por anticlinales del sistema de fallas de
Anaco, en superficie y en el subsuelo (Gonzáles de Juana, 1980).
La Subcuenca de Guárico es una depresión estructural de rumbo este-noreste localizada en la
parte central de Venezuela, comprende los estados Guarico y la parte norte de Anzoategui. Tiene
aproximadamente 300 km de longitud y 120 km de ancho, se encuentra delimitada al norte por el
Corrimiento frontal del Sistema de Caribe, al sur por el Escudo de Guayana, al oeste por el Arco de el
Baúl y al este con el Corrimiento de Anaco. En el flanco norte de la cuenca esta asociado al frente de
deformación, donde se encuentra el sistema de fallas de Guarico el cual sobrecarga rocas cretácicas y
terciarias, produciendo en arco tectónico complejo. Hacia el sur de la estructura se encuentran
depresiones estructurales en las que se preservaron rocas jurasicas y paleozoicas, además se observa
un acuñamiento de las secuencias cretácicas y terciarias en la misma dirección (Ostos y Yoris, 1997).
Es clasificada como tipo “foreland” o antepaís, es asimétrica de norte a sur, abierta hacia el este,
limitada por las planicies costeras sobre su flanco occidental y meridional y profundiza hacia el norte y al
este, (Márquez, 2003). El relleno actual de la subcuenca de Guárico tiene un espesor máximo de 5 km,
aunque puede variar entre 3 y 4 km, Figuras 4.8a y 4.8b. Esto no incluye más de 3km de sedimentos
erosionados desde el Oligoceno (Erlich et. al.,1992).
48
Figura 4.7: Mapa de Ubicación de la Cuenca Oriental de Venezuela. Modificado de Yoris F. y Ostos M., 1997.
Al igual que la subcuenca de Guarico la subcuenca de Maturín es una cuenca antepaís y se
encuentra ubicada en el nor-este de Venezuela, extendiéndose desde el frente de deformación en el
norte (sur de la Serranía del Interior) hasta el río Orinoco al sur, y limita al oeste con la sub-cuenca de
Guárico y al este con el océano Atlántico (González de Juana, 1980), Figura 4.7. Toda la cuenca
presenta un suave declive hacia el norte. Su columna sedimentaria se compone casi exclusivamente de
areniscas y lutitas, con edades que van desde el Cámbrico Inferior al Pleistoceno, y su espesor varia
desde unos pocos metros al sur hasta más de 10 km en las cercanías de la Serranía del Interior al norte
(Méndez, 1985).
49
(a)
(b)
Figura 4.8: Cortes geológicos de la Subcuenca de Guárico: a) zona oeste, Tomado de Carballo (2004), b) zona este, Tomado de
Rondón (2004)
50
4.3.1 PALEOZOICO
Durante el Paleozoico Inferior los continentes estaban unidos en un sólo supercontinente
denominado Pangea (todas las tierras); sin embargo, al norte de Venezuela existía un mar primitivo
Paleozoico (Méndez, 1985).
La Cuenca Oriental Venezolana formaba parte de una extensa cuenca pericratónica que incluía a
las actuales Cuencas de Barinas, Apure y de los Llanos Orientales de Colombia (Méndez, 1985).
Según González de Juana (1980) se reconocen tres ciclos sedimentarios por separados: el primero
corresponde al Paleozoico Medio-Superior, el segundo comienza durante el Cretácico Medio y se hace
regresivo durante el Terciario Inferior y el tercero se desarrolló durante el Terciario Superior y fue
definitivo para la configuración de la cuenca en su estado actual. Estos tres ciclos sedimentarios tienen
lugar entre períodos principales de orogénesis y después de largos períodos de erosión, cuando las
aguas transgredieron sobre tierras previamente peniplanadas.
En la evolución tectónica Post-Paleozoica de las cuencas antepaís de Venezuela pueden
distinguirse tres etapas principales: La Tectonosecuencia de Ruptura, en el Jurasico Tardío; La
Tectonosecuencia de Margen pasivo, del Cretácico al Paleógeno (Este) y al Eoceno (Oeste); Las fases
transcurrentes, transpresivas y compresivas, Paleógeno–Cuaternario (Erlich y Barret, 1992).
4.3.2 FASE DE RUPTURA –APERTURA CONTINENTAL “RIFTING JURÁSICO”
La Tectonosecuencia de Ruptura, ruptura de Pangea y subsecuente divergencia de las placas
Norte y Sur Americana, esta fase extensiva desarrolló progresivamente el Graben de Espino (Pindell and
Dewey,1982; Summa et al., 2003). Esta tectonosecuencia también ha sido asociada a la apertura del
Atlántico Sur durante el Cretácico Temprano (González de Juana, 1980).
51
4.3.3 MARGEN PASIVO
El margen pasivo en la parte central y oriental de Venezuela fue producido por la subsidencia
termal post-rift durante el Cretácico al Paleógeno, en el este de la Cuenca Oriental y del Cretácico al
Eoceno en el oeste de dicha cuenca. Sedimentos siliciclásticos y carbonáticos fueron depositados en
respuesta a subsidencias tectónicas y cambios eustáticos globales del nivel del mar (Di Croce, 1995).
Información de registros de pozos confirmaron que el origen de los sedimentos fue principalmente desde
el sur (Escudo Guayanés) y el oeste (Arco El Baúl). No ocurrieron episodios tectónicos mayores durante
este tiempo, como resultado es posible interpretar la estratigrafía del margen pasivo en el centro-este de
Venezuela y en la Serranía del Interior como procesos controlados por los cambios en el nivel del mar
(González de Juana, 1980).
Debido a la subsidencia termal ocurrida en este periodo, sobre el margen
meridional de
Suramérica se depositan sedimentos de espesores variables, entre pocos centenares de metros en los
bordes septentrional y meridional, hasta 2000 m en la región central perteneciente a la subcuenca de
Guárico. Estos sedimentos acumulados son predominantemente marinos y carbonáticos, en el Cretácico
Temprano. El margen pasivo es modificado diacrónicamente de oeste a este. En el oeste se extiende del
Cretácico Tardío al Paleoceno, en el centro hasta el Eoceno y en el este hasta el Mioceno Superior
(González de Juana, 1980).
A lo largo del Cretácico ocurre la máxima transgresión marcada por la depositación de arenas y
carbonatos plataformales que se formaron diacrónicamente de norte a sur en toda la Cuenca Oriental,
donde se incluye la Fm. Barranquín (Barriniense), Fm. El Cantil (Albiense), Fm. Querecual y la Fm. San
Antonio (Cenomaniense-Campaniense) y hacia el sur la Fm. El Tigre (Tearpock et.al,1998), Figura 4.9.
52
Figura 4.9: Columna Estratigráfica de la Cuenca Oriental de Venezuela. Tomado del L.E.V, 1997.
53
Luego de la máxima regresión del Maastrichtiense representada por la Fm. San Juan en la
subcuenca de Maturín, ocurre la segunda etapa transgresiva durante el Paleoceno-Eoceno, donde se
depositaron las Fm. Vidoño y Caratas (Tearpock et.al,1998), ver Figura 4.9. La fase extensional menor
ocurrió durante la sedimentación de secuencias Cretácica (Pérez de Armas, 2005).
4.3.3 MARGEN ACTIVO - ANTEPAÍS “FORELAND” TERCIARIO
En el Eoceno Temprano y Medio, las secuencias de margen pasivo occidentales son modificadas
por movimientos transpresivos dextrales en el oeste de la Placa Suramericana. La zona central de
Venezuela fue también afectada por esta tectonosecuencia en el Eoceno Temprano-Mioceno Temprano.
Esta deformación continúa hasta el presente por la
interacción entre la Placa del Caribe y la
Suramericana (Márquez, 2003).
La transición de margen pasivo a margen activo se evidencia con las rocas metamórficas de la
Codillera del Caribe, correspondientes a las napas emplazadas hacia Suramérica por el movimiento de la
Placa del Caribe durante el Eoceno Temprano, comprimiéndose posiblemente durante el Paleoceno
(González de Juana, 1980), ver Figura 4.10.
La primera evidencia estratigráfica registrada del levantamiento en la Cuenca Oriental la
constituyen los sedimentos del Oligoceno Tardío, pero el intervalo conglomerático tardío sugiere que el
emplazamiento de las napas produjo subsidencia, lo que permitió la acumulación de sedimentos. El
mayor volumen de sedimentos en la Cuenca Oriental derivó del Cratón de Guayana, aunque el
corrimiento y la deformación Terciaria también aportaron sedimentos a la cuenca (Speed, 1985).
El fallamiento durante el Terciario Inferior fue significativo, pero de poca magnitud en el área de
Guárico Oriental. El fallamiento normal se desarrolla en el foreland antes del cinturón plegado, a medida
que la corteza se sobrecarga y se dobla por debajo de los sobrecorrimientos (Bradley y Kidd, 1991).
54
Figura 4.10: Migración del frente de Deformación del Caribe hacia el este-suroeste en el norte de Venezuela.
Tomado de Yoris F. y Ostos M., 1997.
En la subcuenca de Guárico muchas de las fallas del Terciario son desarrollos tardíos de fallas
del Jurásico, que mueren contra la parte inferior de la Fm. Chaguaramas. También debido a que las fallas
están atravesando rocas menos competentes, estas suelen dividirse en una serie de fallas o fallas
secundarias antitéticas (D’Aubeterre, 2004).
Durante el Eoceno medio-superior el mar invade la Cuenca Barinas, comunicándose
abiertamente con la Cuenca Oriental. El mar se retira más al norte y quedan expuestos a la erosión
subaérea los sedimentos costeros del Cretácico Superior, lo que vino a originar la gran discordancia que
eliminó las rocas de este período en la parte meridional de la cuenca (Méndez, 1985).
La pulsación orogénica del Eoceno superior o emplazamiento de las napas de Lara produjo dos
fenómenos fundamentales en la evolución Terciaria de la cuenca: el hundimiento de la parte occidental
55
en el área de Guárico, que ocasionó a invasión marina y la subsecuente sedimentación de las
Formaciones Las Pascua y Roblecito, y el levantamiento de la Serranía del Interior Central (Cordillera de
la Costa), marcado por el hiato paleontológico constatado entre la Fm. Caratas, Miembro Tinajas y la Fm.
Los Jabillos. Es sólo a partir de este período geológico cuando comienza el desarrollo de la Cuenca
Oriental de Venezuela en su sentido más estricto (Méndez, 1985; Pérez de Armas, 2005).
Los Grupos Guayuta y Temblador están sobrecorridos actualmente por el Frente de Deformación
del Norte de Guárico. Estos grupos son la roca madre principal de la subcuenca de Guarico, se piensa
también que el avance de las napas llevó rápidamente a esta roca madre a ventana de gas por carga
tectónica, al menos desde el Eoceno Tardío, por esto la principal acumulación al sur del Frente de
Montañas es de gas (González de Juana et al., 1980).
Ha sido de gran interés estudiar el origen de los grandes volúmenes de gas que se han
reconocido al noroeste de la Cuenca Oriental de Venezuela, i.e., la Subcuenca de Guárico, para lo que
se consideran dos hipótesis:
1.- El gas y los condensados fueron resultado de ambientes sedimentarios no marinos o poco
marinos, atribuibles a las formaciones terciarias de Guárico.
2.- Las columnas de soterramiento y el grado geotérmico encontrado en Guárico, más elevado
que el encontrado en el área de oficina, contribuyeron a producir gases y condensados de petróleos
livianos generados con anterioridad. (González de Juana et al., 1980)
El levantamiento generalizado de la Cordillera metamórfica Central en la parte norte de la
subcuenca de Guarico trajo como consecuencia la incorporación el surco de Guárico como área
emergida (Méndez, 1985)
56
La depositación de la
Fm. La Pascua (transgresiva) y la Fm. Roblecito (foredeep) es
contemporánea con el desarrollo o reactivación de estructuras extensionales en terrenos alóctonos de la
Placa Suramericana, durante la formación de la antefosa o “foredeep” de Guarico en el Eoceno tardíoOligoceno Temprano (Pérez de Armas, 2005). Estas estructuras se extienden bien al sur de la cuenca y
podrían haber sido formadas en respuestas a la flexura debida al emplazamiento de las napas de Lara
hacia el Cratón de Guayana y a la peneplenización del cinturón Paleozoico (Summa et al., 2003).
Méndez (1985) plantea en el Oligoceno Inferior se inicia el levantamiento de la Serranía del
Interior, aunque el plegamiento comenzó posiblemente en el Oligoceno Superior-Mioceno Inferior según
dicho autor, y fue causado por la compresión producida por masas metamórficas existentes en el Caribe,
que quizás desde el Cretácico se desplazaban hacia el sur.
En el Mioceno se producen cambios importantes en la forma de la Cuenca Oriental y en la
distribución de los sedimentos. Durante Mioceno Inferior–Medio continua el retiro del mar completándose
el relleno con la sedimentación de la Fm. Chaguaramas. En el Mioceno medio a superior, el mar de la
Cuenca Oriental se profundiza desde el oeste hacia el este, definiéndose tres provincias: nerítico-costero
en Guárico (Fm. Chaguaramas), relleno del “foredeep” o antefosa (Gonzáles de Juana, 1980; Fasola et
al.1985; Kisser, 1997), complejo fluviodeltaico en Anzoátegui y Monagas (Fm. Oficina) y marino abierto
hacia el este (Fm. Carapita). En la parte norte de Guárico la sedimentación se hace predominantemente
continental (D’Aubeterre, 2002). En la Figura 4.11 se presenta un esquema evolutivo de la subcuenca de
Guarico a partir del Mioceno Inferior Medio al Oligoceno Inferior.
Algunas de las fallas normales desarrolladas o reactivadas en el Eoceno Tardío-Oligoceno
Temprano, durante el inicio del “foredeep” o antefosa de la subcuenca de Guarico, fueron posiblemente
invertidas durante el evento tectónico del Mioceno medio (Pérez de Armas, 2005).
57
En la subcuenca de Maturín se depositó en el norte y sur de la cuenca sedimentos de edad
Mioceno Inferior, marcando el cambio de una cuenca de margen pasivo a una cuenca antepaís con activa
subsidencia y depositación. Los sedimentos fueron depositados como respuesta al primer levantamiento
relacionado al emplazamiento de la Serranía del Interior durante el Terciario; el espesor de los mismos
decrece hacia el sur (en tierra y costa afuera). Renovados empujes con una fuerte componente norte-sur
ocasionaron grandes líneas de sobrecorrimiento hacia el sur, como son los corrimientos de Pirital y Anaco
(Di Croce et.al, 1995). Esos mismos empujes produjeron fallas transcurrentes, como la Falla de Urica y
San Francisco (Méndez, 1985).
Los depósitos sinorogénicos del Mioceno Medio están localizados en un área elongada al sur del
Cinturón de Cabalgamientos y al norte del frente de deformación. La Serranía del Interior actual fue
levantada durante este tiempo con una orientación de N70ºE. Al sur de la Serranía se encuentran 3
depocentros que fueron formados en diferentes épocas, indicando la migración de los cabalgamientos de
la Serranía de oeste a este, y la subsecuente subsidencia de la corteza de la Cuenca de Maturín causada
por la carga de los cabalgamientos. El depocentro más profundo se encuentra al nor-este, indicando una
intensificación de la carga en esta área durante el Mioceno Medio. Las secuencias más delgadas están
en el nor-oeste (debido a la erosión como resultado de los cabalgamientos recientes) y hacia el sur (Di
Croce et al., 1995).
Al parecer, las formaciones del Mioceno muestran la presencia de sedimentos de proveniencia
septentrional, lo que sugiere que en el Mioceno la Serranía del Interior Oriental fue siempre una
característica positiva al Norte de Venezuela, pero el proceso de colisión podría haber comenzado en el
Oligoceno Temprano (Speed, 1985).
El Mioceno Superior es más delgado, lo que puede indicar que fue depositado en un ambiente
tectónico menos activo, con una baja rata de subsidencia. La secuencia más gruesa se encuentra en el
58
medio de la cuenca, relacionada a un sistema de fallas lístricas que afectó la Cuenca de Maturín durante
este tiempo. Hacia el nor-oeste las unidades son delgadas y erosionadas (Jácome et al., 2003).
La subsidencia del Plioceno y del Pleistoceno ha sido localizada al este de la Cuenca de Maturín,
donde no hay evidencia de carga tectónica por corrimientos. Al nor-noroeste la unidad adelgaza y se
encuentra sobre los corrimientos. La fuente de sedimentos fue la Serranía del Interior al norte y el Cratón
de Guayana al sur. Se distinguen 3 depocentros: en el sur del Golfo de Paria (en tierra), relacionado a los
depósitos del Delta del Orinoco; sur de Trinidad (costa afuera) y sur del prisma de acreción de Barbados
(costa afuera), ambos relacionados a sistemas de fallas en crecimiento (Di Croce, 1995). Los
depocentros son más anchos que los del Mioceno y han migrado de oeste a este asociándose a un
migración sur-este de la Serranía del Interior (Jácome et al., 2003).
Un evento tectónico post-Mioceno levantó, peneplenizó e inclino hacia el este la cuenca de
Guarico. Extensión Neogéna y más reciente es observada en toda la cuenca, deformando secuencias
Oligocenas (Pérez de Armas, 2005). Basados en un análisis 2D de data sísmica, Blanco et al.(1998) y
Daal y Lander (1993) sugieren que estas fallas normales tienen una tendencia NE-SO.
El acortamiento en la Cuenca de Maturín decrece de oeste (50 km) a este (35 km). El espesor de
sedimentos, sin embargo, incrementa de oeste (7 km) a este (10 km), indicando que no parece haber
relación directa entre el acortamiento y la acumulación de sedimentos (Jácome et al., 2003)
59
N
2
S
MIOCENO INFERIOR MEDIO
OLIGOCENO SUPERIOR
OLIGOCENO MEDIO (parte media)
OLIGOCENO MEDIO (parte inferior)
1
OLIGOCENO INFERIOR (parte superior)
OLIGOCENO INFERIOR (parte media)
OLIGOCENO INFERIOR (parte inferior)
Figura 4.11: Esquema evolutivo de la Subcuenca de Guarico: 1) Secuencia Transgresiva , 2) Secuencia Regresiva. Modificado de
Fernández, 2004. (Lambertini et. al., 1987).
60
En el Plioceno se establecieron ambientes fluviodeltaicos y neriticos costeros, consecuencia del
continúo retroceso del mar hacia el este. En estos ambiento se sedimenta la Fm. Las Piedras (Méndez,
1985).
La culminación del proceso ambiente continental y edad Pleistocena sedimentario de la Cuenca
Oriental esta representado Fm. Las Mesas (Méndez, 1985).
La Cuenca Oriental de Venezuela como ya se menciono antes es parte de un “foreland” o cuenca
antepaís involucrado en un cinturón de plegamiento y corrimiento asociado al emplazamiento de los
terrenos del caribe al norte de Sudamérica. Las estructuras más importantes a nivel regional son:
4.4.1 Cordillera de la Costa
La Cordillera de la Costa pertenece al Sistema Montañoso del Caribe, el cual también incluye las
siguientes unidades: las Islas Holandesas y Venezolanas, la Franja Costera, Caucagua-El Tinaco, Loma
de Hierro, Villa de Cura, Formación Dos Hermanas y la zona Piemontina, (Beck, 1983; Bellizzia, 1986;
Navarro et al., 1988; Ostos, 1990; Beccaluva et al., 1996; Giunta et al., 1997). Esta unidad representa el
sustrato de las unidades de la Franja Costera y Caucagua-El Tinaco (Giunta et al., 2003), ver Figuras
4.10 y 4.11. Este cinturón aflora en un alto estructural estrecho, que se extiende desde Barquisimeto a
Trinidad (Giunta et al., 2003) y está formado por un basamento continental Precámbrico-Paleozoico
Temprano (Complejo de Sebastopol, Beck, 1985; Bellizzia, 1986) y por una cubierta de carbonatos
terrígenos (Jurásico Tardío-Cretáceo) con intercalaciones volcánicas locales (formaciones Las Brisas,
Las Mercedes y Chuspita, Beck, 1985; Bellizzia, 1986).
Este orógeno se extiende aproximadamente 1000 km de longitud y 350 km de ancho, de los
cuales 100km se encuentran sobre la litosfera continental suramericana (Giunta et al. 2002).
61
La Cordillera Central separa dos grupos de corrimientos: al norte la unidad de la Cordillera de la
Costa se encuentra sobrecorrida por la Franja Costera y parte de la unidad Caucagua-El Tinaco, y al sur
por las unidades Caucagua-El Tinaco, Loma de Hierro, Villa de Cura y Dos Hermanas (Giunta et al.
2002). La porción del orógeno que se encuentra sobre litosfera continental ha sobrecorrido las unidades
de la Faja Piemotina hacia el sur (Giunta et al. 2002).
La Unidad de Caucagua-El Tinaco aflora en contacto tectónico con la Unidad de la Cordillera de
la Costa a lo largo de la Falla de La Victoria (Figuras 4.12 y 4.14) (Giunta et al., 2003).
Figura 4.12: Mapa geológico esquemático y cross-secciones del Sistema Montañoso del Caribe. 1) Arco Volcánico de las Antillas
Menores y Aves; 2) Depósitos terrígenos terciarios; 3) Zona Piemontina; 4) Islas Holandesas y Venezolanas; 5) Unidad Dos
Hermanas; 6) Unidad de Villa de Cura; 7) Unidad de la Franja Costera; 8) Unidad de Loma de Hierro; 9) Unidad de Caucagua-El
Tinaco; 10) Unidad de la Cordillera de la Costa; 11) Placa Suramericana (Modificado de Giunta et al., 1997).
62
4.4.2 El Surco de Guárico
El surco de Guarico se desarrolla hacia el noroeste de la Cuenca Oriental de Venezuela, este posee un
espesor aproximado de 4000m y pertenece la Faja Piemontina. Este Surco esta limitado al norte por una
serie de corrimientos (entre ellos el Corrimiento de Cantagallo) y por la falla de La Puerta, al sur, limita
con el Corrimiento frontal de Guarico. La Fm. Guárico es la unidad característica de este surco, y esta
conformada por una secuencia tipo “flysh” (calizas y lutitas turbiditicas) de surco profundo, que están
presentes en los contrafuertes montañosos al norte (Lambertini et al., 1987).
4.4.3 Corrimiento Frontal de Guarico: este sistema de corrimientos esta situado al norte de la cuenca
con una longitud aproximada de 400 km y representa el límite septentrional del sector noroeste de la
Cuenca Oriental de Venezuela (Gonzáles de Juana, 1980). Ver Figura 4.13.
Figura 4.13: Principales elementos estructurales en la Cuenca Oriental de Venezuela.
Modificado de CEPET, 1989.
63
4.4.4 Cinturón de plegamientos y cabalgamientos de la Serranía del Interior Oriental
El cinturón de plegamientos y cabalgamientos antepaís de la Serranía del Interior ocupa grandes
áreas de Venezuela nor-oriental; el límite norte de esta provincia es la falla de El Pilar, Figura 4.14. Las
tendencias estructurales son principalmente NE a E y consisten de estratos plegados cretácicos y
paleógenos, y sedimentos menos deformados (estos estilos estructurales incluyen superficies de
despegue plegadas, cabalgamientos y fallas rumbo-deslizantes) (Di Croce, 1995).
La transición entre el cinturón de cabalgamientos de la Serranía del Interior y la cuenca antepaís
de Maturín contiene rocas pre-cretácicas, cretácicas y terciarias que han sido plegadas y cabalgadas. El
Mioceno Inferior y Medio es una cuña acrecionaria que descansa sobre una sucesión cabalgada de
margen pasivo. La secuencia desde el Mioceno Superior hasta el Plioceno-Pleistoceno se encuentra en
forma de “onlaps” sobre el cinturón plegado emergente. Existen dos fases de deformación con distintos
niveles de superficies de despegue activados sucesivamente y relacionados al emplazamiento de la
Serranía del Interior: el primero involucra una superficie de despegue intra-cretácica a terciaria somera y
una profunda pre-cretácica, y una segunda fase reactivó estructuras pre-cretácicas más profundas hasta
estructuras más viejas (Jácome et al., 2003).
4.4.5 Falla de Urica: lineamiento transcurrente de componentes dextrales ubicado desde la zona petrolera
de Tacata y siguiendo por la línea fronteriza entre los Estados Anzoátegui y Monagas hasta el NE de la
población de Úrica. Posee una extensión lineal de 107 km, aproximadamente. Su traza se pierde al sur de
Barcelona. Esta falla se considera como el límite meridional del Bloque de Paria y límite a su vez del
flanco sur de la Subcuenca de Maturín (Rod, 1956), ver Figuras 4.13 y 4.14.
4.4.6 Corrimiento Pirital: desde la Falla de Úrica hasta la Falla de San Francisco continúa el sistema de
corrimientos frontales de Guárico y Anzoátegui. Entre las numerosas fallas inversas de este sistema
64
destaca el Corrimiento de Pirital. Se encuentra en la parte meridional de la Serranía del Interior (Gonzáles
de Juana, et al. 1980). De Sito (1961) define la falla inversa de Pirital como un cabalgamiento de
sedimentos Cretácicos hasta el Oligoceno sobre la Formación Carapita. Según Parnaud et el. (1995) este
corrimiento es producto del emplazamiento progresivos de varios compartimientos alóctonos de la
Serranía produciendo el principal corrimiento norte-sur, ver Figuras 4.13 y 4.14.
4.4.7 Graben de Espino: elemento estructural de más de 300 km de largo por 50 km de ancho (Bartok,
1993) se extiende en sentido Sureste –Noreste bajo el margen pasivo Cretácico-Paleógeno y el relleno
antepaís de la Cuenca Oriental de Venezuela. Se prolonga hasta la Cuenca Barinas-Apure, separado de
esta por el Arco del Baúl (Feo-Codecido et al., 1984). Ver Figura 4.14.
4.4.8 Corrimiento Anaco: se encuentra en la parte central del Edo. Anzoátegui con un rumbo promedio
N45E y buzamiento de 45° al noreste y longitud aproximada de 85km, Figuras 4.13y 4.14. El corrimiento
de Anaco es una estructura relativamente joven que tiene desplazamiento de unos 4000 pies, localmente
pone el contacto Mioceno Inferior con Mio-Plioceno.
De acuerdo con Parnaud et al. (1995), el corrimiento de Anaco se forma dentro de una cuenca
antepaís que se desarrolla en el Neogéno sobre el margen pasivo Mesozoico, por las fuerzas compresivas
que actúan sobre la placa Suramericana. La estructura se origina como una profundización de una falla
normal al noroeste y formación de un bloque deprimido. Al igual que la sedimentación esta estructura se
empieza a formar durante el Oligoceno Temprano (Banks y Driver, 1957).
65
Falla El Coche
Falla El Pilar
Falla de San
Francisco
Falla de
Urica
Corrimiento Pirital
Corrimiento de
Anaco
Figura 4.14: Serranía del Interior Oriental y sus fallas más importantes. Modificado de Maceda, 2005
66
El presente análisis de subsidencia (basado en isostasia tipo Airy, 1D) involucra esencialmente
tres pasos, comenzando por la medida del espesor de cada unidad estratigráfica, edad y su respectiva
paleoprofundidad. El segundo paso es la descompactación de la columna estratigráfica, para esto es
necesario que la variación de porosidad con la profundidad sea conocida, en este caso, se tomó la
relación hallada por Sclater y Christie (1980), además se utilizaron los valores de porosidad superficial y
coeficiente de profundida-porosidad característicos para cada litología, determinados por estos autores,
(Tabla 5.1). El tercer paso en este análisis de subsidencia es el “backstripping” (Watts y Ryan, 1976) o
retro-evolución, es decir, la remoción del efecto de la carga sedimentaria y del agua (subsidencia
sedimentaria) de la subsidencia total para obtener la subsidencia tectónica. Para el cálculo de la
subsidencia isostática o sedimentaria se consideró la paleobatimetría y las variaciones eustáticas del
nivel del mar. Para mayor explicación acerca de la técnica de retro-evolución (backstripping) ver el
capítulo 3.
Litología
Porosidad Superficial
c ( 1/ km)
Lutitas
0.63
0.51
Areniscas
0.49
0.27
Areniscas limosa
0.56
0.39
Tabla 5.1: Parámetros de porosidad-profundidad para litologías del Mar del Norte. Donde c es el coeficiente de porosidadprofundidad. Tomado de Sclater y Christie (1980)
Para obtener mayor información del área de estudio fue necesario realizar una integración de
toda la información disponible: datos de pozos, líneas sísmicas (suministradas por PDVSA Exploración) y
previamente interpretadas (Santiago et al., 2004; Jacome et al., 2003) y la geología publicada del área. A
partir de estos datos se crearon seudo-pozos o secciones características para cuatro regiones
representativas de la Cuenca Oriental de Venezuela (Maturín Norte, Maturín Centro, Maturín Oeste y
Guarico). A continuación se presenta una descripción detallada de cómo se integro la información en los
casos estudiados.
66
67
5.1.1 MATURIN NORTE
En Maturín Norte se decidió tomar el perfil de temperatura del pozo B-3, ya que presenta datos
de temperatura hasta basamento. Además el perfil de temperatura de este pozo representa
bastante bien el comportamiento termal característico de esa zona, debido a que los perfiles de
esa área son similares. En el próximo capitulo se muestra este perfil.
Se construyo la sección característica de esta región tomando en cuenta el pozo B-3 y los
espesores promedios de las formaciones presente en esa área (L.E.V, 1997), para contar con
una columna los más completa posible. La profundidad del basamento obtenida fue
adicionalmente comparada con información sísmica (Fernández, 2004). Tabla 5.2.
Para estimar la Paleobatimetría correspondiente a cada unidad o formación se considero
publicaciones previas (L.V.E.,1997; Pindell y Erikson, 1993). Las variaciones eustáticas del nivel
del mar se calculó mediante la curva publicada por Haq en 1987, ver Apéndice B.
A continuación se presenta la localización de los pozos considerados para el análisis de esta
zona. Figura 5.1
B-3
Maturín
Norte
Figura 5.1: Localización del perfil B-3 y los pozos cercanos.
68
Pozo
Profundidad(m)
T(ºC)
Fm.
Litología
Edad
B-3
0,309
58
La Pica
Lutitas
Mio. Tardío
B3
1,306068
71
Carapita
Lutitas
Mio. Temprano
B-3
4,1169336
144
Naricual
Lutitas
Olig. Tardío
B-3
4,6686216
154
Los Jabillos
Arenicas
Olig. Temprano
B-3
5,0819304
166
**
Areniscas
Cretácico Superior
Sísmica
6680
?
Barranquín
Areniscas
Cretácico Temp.
Tabla 5.2: Información seleccionada, Maturín Norte. (**) Incluye varias formaciones del Cretácico Superior
5.1.2 MATURÍN CENTRO, MATURÍN OESTE Y GUARICO
El proceso se integración es esta tres regiones es similar, así que se explicara en conjunto.
Se construyo el perfil de temperatura característico de cada región tomando en cuenta pozos
cercanos, ver Figura 5.2. La información tomada de los pozos seleccionados se resume en la
siguientes tablas (Tabla 5.3, Tabla 5.4 y Tabla 5.5). Los perfiles de temperatura compuestos se
muestra en la próximo capitulo.
Pozo
Profundidad(m)
T(ºC)
Fm.
Litología
Edad
D-2
0,7324344
47,7
Las Piedras
Areniscas
Mio.Tardio-Plio
N-2
2,7761184
77
Quiamare
Arcilitas
Mioceno Tem
N-2
3,128772
86,2
Quiamare
Arcilitas
Mioceno Tem.
N-2
3,2708088
83,7
Quiamare
Arcilitas
Mioceno Tem.
N-2
3,5484816
91,7
Quiamare
Arcilitas
Mioceno Tem.
D-2
5,2142136
138,1
San Juan
Areniscas
Paleoceno Temp.
D-2
5,670804
158,9
Barranquin
Areniscas
Cretacico Temp.
Tabla 5.3: Información seleccionada, Maturín Centro
69
Pozo
Profundidad(m)
T(ºC)
Fm.
Litología
Edad
I-2
0,9668256
50,7
Areniscs
Plioceno
E-2
1,2716256
66,4
Mesa
Las
Piedras
Areniscas
Mio.Tardio
E-2
2,3310336
114,1
Quiamare
Arcilitas
Mioceno Tem
E-2
2,6371296
140,9
Quiamare
Arcilitas
Mioceno Tem
Z-2
4,1871888
165,2
Naricual
Lutitas
Olig. Temp
Z-2
4,8268128
158
Naricual
Lutitas
Olig. Temp
Tabla 5.4: Información seleccionada, Maturín Oeste.
Pozo
Profundidad(m)
T(ºC)
Fm.
Litología
Edad
M-1
0,3048
38
Quiamare
Arcilitas
Mio. Tem.
F-1
1,2889992
86
Roblecito
Lutitas
Olig.
F-1
2,0196048
98
Roblecito
Lutitas
Olig.
F-1
2,0875752
110
Roblecito
Lutitas
Olig.
D-1
2,1802344
136
Roblecito
Lutitas
Olig.
S-1
2,260092
156
San Juan
Areniscas
Paleoceno Tem
F-1
2,6267664
139
San Juan
Areniscas
Paleoceno Tem
Tabla 5.5: Información seleccionada, Guarico
Luego se tomó los espesores promedios de las formaciones consideradas (L.E.V, 1997). Las
secciones compuestas se presentan en la Figura 5.3. La profundidades del basamento fueron
comparadas con información sísmica (Fernández, 2004). Para la estimación de la paleobatimetría
y las variaciones eustáticas del nivel del mar se considero publicaciones previas (L.V.E.,1997;
Pindell y Erikson, 1993; Haq, 1987), ver Apéndice B.
70
S1
D1
F1
M1
Maturín
Oeste
E2
I2
Z2
Guarico
D2
N2
Maturín
Centro
Figura 5.2: Ubicación de los pozos seleccionados para construir la sección característica de Maturín Centro, Maturín Oeste y
Guárico.
71
(a)
0 km
(b)
(c)
2
(d)
Aptiense
Olig. Tardío
Cretácico Tardío
Mioceno Temprano
Paleoceno
Mio. Tardío
Plioceno
Olig. Temprano
Pleistoceno
Figura 5.3: Secciones Compuestas: (a) Guarico, (b) Maturín Oeste, (c) Maturín Centro y (d) Maturín Norte
A continuación se presenta los resultados y análisis de cada uno de los casos estudiados:
5.2.1 MATURIN NORTE
Las curvas de subsidencia para cada unidad descompactada en Maturín Norte se presentan en la
Figura 5.4.
72
En las Figuras 5.4 y 5.5 se observa que a partir del Aptiense (121Ma) hasta el Oligoceno
Temprano (28Ma) las curvas muestran un comportamiento tipo Margen Pasivo (Gonzáles de Juana,
1980; Erikson, 1992; Erikson y Pindell, 1993). Las tasas de subsidencia durante este tiempo, fueron
bajas, entre 22.22 y 11.16 m/Ma (sedimentos compactados) y entre 38.43 y 17.42 m/Ma (sedimentos
descompactados), Figura 5.6.
A partir del Oligoceno Temprano (28Ma) aumenta la subsidencia, marcando el cambio de la
cuenca de margen pasivo a una cuenca antepaís con activa subsidencia y depositación, debido a que el
acercamiento del Caribe, desde el oeste, comienza a afectar los terrenos de Venezuela Oriental (Pindell y
Kennan, 2001).
Las tasas de subsidencia durante el Margen Activo, fueron mucho más altas que durante el
Margen Activo. Para sedimentos compactados oscilaron entre 110.4 y 175.26 m/Ma, y para los
sedimentos descompactados entre 202.6 y 175.26 m/Ma, ver Tabla 5.6 y Figura 5.6.
En la Figura 5.5 la curva de subsidencia tectónica muestra un levantamiento o rebote isotático
del Margen Pasivo en el Oligoceno Temprano (28Ma), también apreciable en la Figura 5.6. Pindell et al.
(1998) propone que la convergencia entre Norte y Sur América comenzó durante el Paleoceno, y en el
Eoceno medio el acortamiento pudo haber sido de aproximadamente 70km (Pindell, 1997), lo cual se
manifestó posteriormente por el engrosamiento estructural, levantamiento y erosión del margen pasivo.
Además Pindell et al. (1998) sugieren que esta contracción entre las Placas Norte y Sur Américanas
podría haber deformado la corteza Proto-Caribeña, formando una incipiente zona de subducción.
En el Mioceno Temprano (16Ma) también se observa un rebote isotático pequeño, posiblemente
asociado al emplazamiento y erosión del Corrimiento de Pirital (Méndez, 1985; Jácome, 2001).
73
120
110
100
90
80
70
Edad (Ma)
60
50
40
30
20
10
0
0
1000
3000
Aptiense
Cretácico Tardío
4000
Oligoceno Temprano
5000
Oligoceno Tardío
Mioceno Temprano
Profundidad (m)
2000
6000
MIoceno Tardío
7000
8000
Figura 5.4: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, Maturín Norte.
110
100
90
80
70
Edad (Ma)
60
50
40
Levantamiento
30
20
10
0
0
Rebote Isostático 1000
2000
3000
Subsidencia Total
Subsidencia Sedimentaria
4000
5000
6000
Subsidencia Tectónica
7000
8000
Figura 5.5: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy (1D), Maturín Norte.
Profundidad (m)
120
74
Edad (Ma)
120
110
100
90
80
70
60
50
40
30
20
10
0
50
100
150
200
250
Sedimentos compactados
300
350
Sedimentos descompactados
400
Tasa de Subsidencia (m/Ma)
0
450
Figura 5.6: Tasa de Subsidencia vs. Edad, Maturín Norte
TASAS
DE
SUBSIDENCIA
(m / Ma)
Edad
Edad (Ma)
Compactado
Descompactado
Diferencia
Mecanismo Asociado
Aptiense
112
22.22
38.33
16.11
Margen Pasivo
Cretácico Tardío
65
29.76
42.89
13.13
Margen Pasivo
Oligoceno
Temprano
28
11.16
17.42
6.26
Margen Pasivo
Oligoceno Tardío
23
110.4
202.6
92.2
Margen Activo
Mioceno
Temprano
16
185.14
275.28
90.14
Margen Activo
Mioceno Tardío
5
176.25
176.25
0.0
Margen Activo
Tabla 5.6: Tasa de Subsidencia y su mecanismo asociado, estratos compactados y descompactados, Maturín Norte.
5.2.2 MATURIN CENTRO
Barranquín (Aptiense), San Juan (Cretácico Tardío), Merecure Superior (Oligoceno), Quiamare
(Mioceno Temprano) y Las Piedras (Plioceno) son las formaciones correspondientes a las unidades
descompactadas de Maturín Centro, Figura 5.7.
75
En la Figura 5.8 se observa que las curvas de subsidencia total, sedimentaria y tectónica
muestran un comportamiento tipo Margen Pasivo a partir del Aptiense hasta el Mioceno Temprano
(Gonzáles de Juana, 1980; Erikson, 1992; Erikson y Pindell, 1993). A los 20Ma ocurre un incremento
notable en la subsidencia, indicando el cambio de Margen Pasivo a Margen Activo en la zona central de
la subcuenca de Maturín, por la colisión entre el Caribe y Suramérica. La subsidencia es diácronica y más
joven en Maturín Centro con respecto a Maturín Norte.
En la Figura 5.9 se muestran las tasas de subsidencia a través del tiempo, para los sedimentos
compactados y descompactados. Las máximas tasas de subsidencia se observan en sedimentos del
Mioceno Temprano (16Ma), 461m/Ma (sedimentos compactados) y 706.5 m/Ma (descompactados). Los
sedimentos del Cretácico Superior (65Ma) presentan las mínimas tasas de subsidencia,
8.44m/Ma
(compactados) y 13.5m/Ma (descompactados). En la Tabla 5.7 se resumen las tasas de subsidencia
tanto para los sedimentos compactados como descompactados y sus mecanismos o Tectonosecuencias
asociadas.
Edad (Ma)
110
100
90
80
70
60
50
40
30
20
10
0
0
1000
Aptiense
2000
Cretácico Tardío
3000
Oligoceno
4000
Mioceno Temprano
5000
Plioceno
6000
7000
Figura 5.7: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, Maturín Centro
Profundidad (m)
120
76
Edad (Ma)
120
110
100
90
80
70
60
50
40
30
20
10
0
0
1000
3000
Subsidencia Total
4000
Subsidencia Sedimentaria
Profundidad (m)
2000
5000
Subsidencia Tectónica
6000
7000
Figura 5.8: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy, Maturín Centro.
Edad (Ma)
110
100
90
80
70
60
50
40
30
20
10
0
0
100
200
300
Sedimentos compactados
Sedimentos descompactados
400
500
600
700
800
Figura 5.9: Tasa de Subsidencia vs. Edad, Maturín Centro
Tasa de Subsidencia (m/Ma)
120
77
TASAS
DE
SUBSIDENCIA
(m / Ma)
Edad
Edad (Ma)
Compactado
Descompactado
Diferencia
Mecanismo Asociado
Aptiense
112
22.22
37.55
15.55
Margen Pasivo
Cretácico
Superior
65
9.70
15.51
5.81
Margen Pasivo
Oligoceno
Temprano
20
7.97
13.288
5.3
Margen Pasivo
Mioceno
Temprano
16
461
706.5
245.5
Margen Activo
Plioceno
2
173.5
173.5
0
Margen Activo
Tabla 5.7: Tasa de Subsidencia y su mecanismo asociado. unidades compactadas y descompactadas, Maturín Centro.
5.2.3 MATURIN OESTE
En la Figura 5.10 se observa las curvas de subsidencia para cada unidad estratigráfica del seudo
pozo de Maturín Oeste, las formaciones aquí representadas son: San Juan (Maastritiense), Naricual
(Oligoceno), Quiamare (Mioceno Temprano), Las Piedras (Plioceno) y Mesa (Pleistoceno).
En Maturín Oeste los resultados obtenidos (Figuras 5.10 y 5.11) indican que el margen pasivo se
observa a partir del Maastrichtiense (65Ma) hasta el Oligoceno Tardío (23Ma), con tasas de
sedimentación bajas, entre 23.52 y 44.03 m/Ma (Tabla 5.8 y Figura 5.12). A partir del Oligoceno la
subsidencia aumenta significativamente, posiblemente como respuesta al levantamiento relacionado al
emplazamiento de la Serranía del Interior durante el Terciario (Di Croce et al., 1995), las tasas de
subsidencia observadas oscilan entre 96.36 y 359.85 m/Ma (Tabla 5.8 y Figura 5.12). La subsidencia es
diacrónica y más antigua en Maturín Oeste con respecto a Maturín Centro.
En la curva de subsidencia tectónica (Figura 5.11) y en la Figura 5.12 se observa un rebote
isostático en el Plioceno (2Ma), que quizás este asociado a una zona positiva (Formaciones
Chaguaramas y Roblecito), remanente de una superficie erosional hacia Guarico y parte de Anzoátegui
(Méndez, 1985).
78
Edad (Ma)
70
60
50
40
30
20
10
0
0
1000
3000
Cretacico Tardío
4000
Oligoceno
Mioceno Temprano
Profundidad (m)
2000
5000
Plioceno
Pleistoceno
6000
7000
Figura 5.10: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, Maturín Oeste.
Edad (Ma)
70
60
50
40
30
20
10
0
0
1000
Profundidad (m)
2000
3000
Subsidencia Total
4000
Subsidencia Sedimentaria
5000
Subsidecia Tectónica
6000
7000
Figura 5.11: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy, Maturín Oeste.
79
Edad (Ma)
60
55
50
45
40
35
30
25
20
15
10
5
0
50
100
150
200
250
300
Sedimentos compactados
350
Sedimentos descompactados
400
Tasa de Subsidencia (m/Ma)
0
450
Figura 5.12: Tasa de Subsidencia vs. Edad, Maturín Oeste.
TASAS
DE
SUBSIDENCIA
(m / Ma)
Edad
Edad (Ma)
Compactado
Descompactado
Diferencia
Mecanismo Asociado
Maastritiense
65
23.52
37.41
13.89
Margen Pasivo
Oligoceno
Temprano
23
24.57
44.03
19.46
Margen Pasivo
Mioceno
Temprano
16
265.14
359.85
94.71
Margen Activo
Plioceno
2
96.36
130
33.64
Margen Activo
Pleistoceno
0
254.2
254.2
0
Margen Activo
Tabla 5.8: Tasa de Subsidencia y su mecanismo, estratos compactados y descompactados , Maturín Oeste.
5.2.4 GUARICO
La Figura 5.13 muestra la representación gráfica de la descompactación en el proceso de retroevolución (backstripping), en esta figura se observa la curva de subsidencia para cada unidad del seudopozo construido para la región de Guarico, representado por las Formaciones: San Juan (Paleoceno),
Roblecito (Oligoceno) y Quiamare (Mioceno Temprano).
80
En la Figura 5.14 se observa que entre el Paleoceno (54Ma) y el Oligoceno Temprano (28Ma), la
subsidencia es tipo Margen Pasivo, este tipo de subsidencia es propuesta por otros autores (Gonzáles de
Juana, 1980; Erikson, 1992; Erikson y Pindell, 1993). En el Oligoceno Temprano (28Ma) se presenta un
cambio de pendiente de las curvas de subsidencia total y tectónica, posiblemente por la colisión de la
placa Caribe con el continente Suramericano (Lugo y Mann, 1995). La subsidencia es diacrónica y más
antigua en Guarico con respecto a Maturín Oeste.
La curva de subsidencia sedimentaria exhibe un comportamiento constante y la curva de
subsidencia tectónica, en cambio muestra un levantamiento o rebote isostático en el Oligoceno (28Ma),
que podría estar vinculado a la anomalía termal presente en Guarico, motivo de estudio en este trabajo.
Pérez de Armas (2005) registra un evento termal durante el Eoceno, en base al análisis de trazas de
fisión de Apatito, y lo relaciona a la convergencia NO-SE de las placas Norteamérica y Suramericana
(Pindell, 1997; Pindell et al., 1998). Este levantamiento también podría estar asociado a la reactivación o
desarrollo de fallas normales durante los primeros estados de formación de la antefosa (foredeep) en la
subcuenca de Guarico, en el Eoceno-Oligoceno Temprano (Peréz de Armas, 2005).
Los sedimentos Paleocenos (54Ma) presentan las tasas de subsidencia más bajas en la región
de Guarico, entre 17.41m/Ma y 24m/Ma (Margen Pasivo). En el presente se identificó la tasa de
subsidencia más elevada, 56.32m/Ma (Margen Activo), Tabla 5.9.
81
Edad (Ma)
60
50
40
30
20
10
0
0
Profundidad (m)
1000
2000
Paleoceno
3000
Oligoceno
Mioceno Temprano
4000
5000
Figura 5.13: Profundidad descompactada vs el tiempo de cada unidad estratigráfica, en Guarico
Edad (Ma)
60
50
40
30
20
10
0
0
Profundidad (m)
1000
2000
Subsidencia Total
Subsidencia Sedimentaria
Subsidencia Tectónica
3000
4000
5000
Figura 5.14: “Backstripping” o Retro-evolución, basados en un modelo isostático tipo Airy, en Guarico
82
Edad (Ma)
60 56 52 48 44 40 36 32 28 24 20 16 12
8
4
0
10
20
30
40
50
60
Sedimentos compactados
70
80
Sediementos descompactados
90
100
Tasa de Subsidencia (m/Ma)
0
Figura 5.15: Tasa de Subsidencia vs. Edad, en Guarico
TASAS
DE
SUBSIDENCIA
(m / Ma)
Edad
Edad (Ma)
Compactado
Descompactado
Diferencia
Mecanismo Asociado
Paleoceno
54
17.41
24.0
6.56
Margen Pasivo
Oligoceno Tardío
28
22.84
37.19
14.35
Margen Activo
Presente
0
56.32
56.32
0
Margen Activo
Tabla 5.9: Tasas de Subsidencia y su mecanismo asociado, sedimentos compactados y descompactados, Guarico.
Gallagher (1989) discutió los errores asociados a las curvas de subsidencia, debido a los
parámetros de compactación y las densidades de los sedimentos empleadas. En este estudio se usaron
casos sintéticos, y se encontró que las incertidumbres asociadas al proceso de retro-evolución
(backstripping) podrían contribuir a fluctuaciones de +100m en las curvas de subsidencia observadas.
Las principales incertidumbres, para esta data en particular, se deben a los siguientes factores:
83
1) Parámetros de descompactación: se asumió una curva exponencial de la forma
φ=φoexp(-cz),
donde φ es la porosidad, φo es la porosidad inicial, y c es un factor de escala promedio que fija la
pérdida de la porosidad con la profundidad, z, (Sclater y Christie, 1980). Incertidumbres en estos
parámetros de descompactación podrían ser importantes, en cualquier data que sea
descompactada. Los valores presentados en la Tabla 5.1 están basados en el estudio de Sclater
y Christie (1980), ya que se desconoce los valores propios de la Cuenca Oriental de Venezuela.
2) Paleoprofundidad: se tomó en base a valores publicados por Erikson y Pindell (1993) y el
Léxico Estratigráfico de Venezuela (1997), estimada bioestratigraficamente para cada formación.
Los valores estimados se encuentra anexos en el Apéndice B.
3) Edad: al igual que la paleoprofundidad, las edades están basadas en estimaciones generales
para cada formación, tomadas del Léxico Estratigráfico de Venezuela (1997), ver Apéndice B.
4) Densidades: debido a que se incluyeron cálculos isostáticos, se debe tomar en cuenta los
valores de densidad asignados a cada edad. Se consideraron valores de densidades propuestos
por Carballo (2004) y Rondón (2004).Ver Apéndice B.
84
Se han desarrollado cuatro modelos numéricos unidimensionales, los cuales logran reproducir
con gran similitud las geotermas características de los casos estudiados: Maturín Norte, Maturín Centro,
Maturín Oeste y Guarico. Estos modelos incorporan los efectos de la conducción de calor vertical,
producción de calor radioactivo y velocidad de fluido, pero por ser 1D no toma en consideración la
conducción de calor lateral.
El dominio computacional es discretizado en un sistema de Grid Cartesiano. Los espaciamientos
verticales del grid utilizados son: 300 m, 400 m y 1000 m, ver Tablas 6.1, 6.4, 6.5 y 6.7. La regiones
modeladas se extienden desde los sedimentos superficiales hasta una profundidad de 80 km. Esta
profundidad es asumida como la profundidad de compensación (Sawyer, 1987). El espaciamiento del
tiempo (∆t) para las calculaciones es gobernado por las condiciones de estabilidad (ver Apéndice A). Para
preservar la estabilidad numérica, el ∆t debe ser más pequeño que la estabilidad límite. En los cuatro
modelos se eligió 5x10-5 Ma.
También se requiere de condiciones de bordes en todos los límites. El tope del límite, definida
como la temperatura superficial se mantuvo constante en los primeros tres modelos (28.33 ºC) y en el
último cambio a 26.48 ºC, según datos de pozos. En el límite basal de los modelos (base de la litosfera
continental) a 80km de profundidad se asumió una temperatura constante de 1400 ºC.
Los modelos obtenidos no son únicos y podrían variar con asunciones diferentes de las
condiciones de bordes, parámetros termales y espesor de la corteza y/o litosfera.
84
85
1) Construcción del archivo de datos, para esto se estimo valores de: conductividad termal,
producción de calor, calor especifico y densidades en sedimentos y en la corteza superior e
inferior, basado en estudios previos (Turcotte y Schubert, 2002;Carballo, 2004; Rondón , 2004).
2) Implementación del programa FDTHERM_1D utilizando el archivo anteriormente creado, además
de los parámetros de referencia que puede escoger el usuario, ver Tablas 6.1, 6.4, 6.5, 6.7.
3) Una vez visualizado el primer resultado y comparando con el modelo observado se procedió a
introducir valores de velocidad de fluido en los puntos de cambio de la geoterma. También se
varió las conductividades termales iniciales si era necesario, al igual que el espesor de la corteza.
4) Cada vez que se introdujo algún cambio en el archivo de datos se corrió nuevamente el programa
para obtener nuevos resultados y luego se comparo con el modelo observado. Este último paso
se repitió hasta conseguir el mejor ajuste entre las curvas que conservara concordancia con el
modelo geológico de cada uno de los pozos compuestos.
A continuación se presentan los perfiles de temperaturas compuestos para cada uno de los casos
de estudio y sus respectivos gradientes, calculados gráficamente (Figura 6.1, Figura 6.2, Figura 6.3 y
Figura 6.4)
Se estimó los gradientes de temperatura de cada región estudiada (Maturín Norte, Maturín
Centro, Maturín Oeste y Guarico), resultando 27.43; 20.35; 31.6 y 45.5 ºC/km, respectivamente, lo que
corroboró que hacia el oeste de la Cuenca Oriental existe un aumento significativo de temperatura
(Fernández, 2004) .
86
Tem peratura (ºC)
0
20
40
60
80
100
120
140
160
180
160
180
0
Profundidad (km)
1
2
3
4
5
6
Figura 6.1: Perfil de temperatura compuesto para Maturín Norte.
Tem peratura (ºC)
0
20
40
60
80
100
120
140
0
Profundidad (km)
1
2
3
4
5
6
Figura 6.2: Perfil de temperatura compuesto para Maturín Centro.
87
Tem peratura (ºC)
0
20
40
60
80
100
120
140
160
180
160
180
0
Profundidad (km)
1
2
3
4
5
6
Figura 6.3: Perfil de temperatura compuesto para Maturín Oeste.
Tem peratura (ºC)
0
20
40
60
80
100
120
140
0
Profundidad (km)
1
2
3
4
5
6
Figura 6.4: Perfil de temperatura compuesto para Guarico.
88
A continuación se presenta los resultados y la discusión de los modelos obtenidos:
6.4.1 Maturín Norte
La Figura 6.5 predice la geoterma continental hasta una profundidad de 80 km en el área de
Maturín Norte. El espesor de la corteza que mejor ajusto las curvas calculada y observada fue de 40 km.
Ávila (2005) a partir de sísmica profunda propone valores anómalos de espesor cortical entre 45 y 50 km,
en este área.
A continuación se presentan dos Tablas (Tabla 6.1 y Tabla 6.2) en las cuales se resumen los
parámetros físicos y computacionales considerados durante el modelado termal en esta región. La Tabla
6.1 contiene aspectos generales del modelado a diferencia de la Tabla 6.2 la cual especifica cada uno de
los parámetros utilizados en los primeros 6 km (sedimentos).
En la Figura 6.6 se compara la curva calculada con la curva observada en los sedimentos, se
observa un buen ajuste del modelo en los puntos donde se tiene control y en los bordes. Los valores de
conductividades termales consideradas son bajas (1.2 – 1.9 W/mºC) en los primeros kilómetros (arcillas)
y aumenta (3.0-3.2 W/mºC) a una profundidad de 4.8 km (areniscas).
Otro aspecto importante a señalar en este modelo es que fue necesario asumir la presencia de
fluidos desplazándose hacia la superficie entre 1.2 y 2.0 km de profundidad para reproducir con mayor
similitud la curva observada. Las velocidades de fluidos utilizadas para modelar en este caso son
pequeñas (x10-11 m/s) y negativas. Para mayores detalles de los valores utilizados ver la Tabla 6.2.
El gradiente geotérmico característico de Maturín Norte calculado es 27,43 ºC/km, un valor
elevado pero dentro del rango típico para una cuenca antepaís (Allen & Allen, 1990).
89
PARÁMETROS
VALORES CARACTERÍSTICOS
CORTEZA
Espesor
40 km
3
Densidad (ρ)
2800 kg/m
Conductividad Termal (k)
3.3 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
H=Ho*exp (-z/h) , Ho=1x10
-10
W/ kg, h=15km
LITOSFERA SUBCORTICAL
Espesor
40 km
3
Densidad (ρ)
3300 kg/m
Conductividad Termal (k)
3.5 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
0 W/ kg
MODELO TERMAL
Temperatura superficial ( To)
28.33 ºC
Temperatura de la base (Tm)
1400 ºC
Flujo de Calor del Manto (Qm)
40 mW/m
Espaciamiento Vertical (∆z)
Espaciamiento de tiempo (∆t)
Número de Nodos
Extensión Vertical del modelo
2
400 m
-5
5 x10 Ma
198
80km
Tabla 6.1: Parámetros y valores característicos generales en la zona de Maturín Norte.
90
Temperatura (ºC)
0
28.33ºC
200
400
600
800
1000
1200
0
Sedimentos
10
Corteza
20
k=3.3 W/ mºC
3
ρ=2900 kg/m
H=Ho*exp(-z/h)
Profundidad (km)
30
40
50
Manto
Litosférico
60
k=3.5 W/ mºC
3
ρ=3300 kg/m
H=0
70
80
1400ºC
Manto
90
Figura 6.5: Geoterma Litosférica Calculada en Maturin Norte
1400
1600
91
Temperatura (ºC)
0
50
100
150
200
0
1
k=1.2
2
Observada
k=1.55
k=1.7
k=1.9
Profundidad (km)
Calculada
3
4
5
k=3.0
6
k=3.2
7
Corteza
8
Figura 6.6: Curvas Observada y Calculada en Maturín Norte, en sedimentos.
250
92
Profundidad (km)
k (W/mºC)
H (W/kg)
3
ρ (kg/m )
V (m/s)
2250
0
0.4
1.2
1.0x10
-10
0.8
1.2
1.0x10
-10
2250
0
1.2
1.2
1.0x10
-10
2250
0
2250
0
1.6
1.2
1.0x10
-10
2.0
1.2
1.0x10
-10
2250
-2.0 x10
-11
2.4
1.2
1.0x10
-10
2250
-2.0 x10
-11
2.8
1.2
1.0x10
-10
2250
-2.0 x10
-11
3.2
1.55
1.0x10
-10
2250
-2.0 x10
-11
3.6
1.55
1.0x10
-10
2250
-1.0 x10
-11
4.0
1.55
1.0x10
-10
2250
-1.0 x10
-11
4.4
1.7
1.0x10
-10
2250
-1.0 x10
-11
4.8
1.9
1.0x10
-10
2250
-1.0 x10
-11
5.2
3.0
1.0x10
-11
2650
0
2650
0
5.6
3.2
1.0x10
-11
6.0
3.2
1.0x10
-11
2650
0
1.0x10
-11
2650
0
6.4
3.2
Tabla 6.2: Parámetros y valores característicos en Maturín Norte, en sedimentos.
6.4.2 Maturín Centro
En la Figura 6.7 se presenta la geoterma continental calculada para Maturín Centro. La geoterma
observada en este caso no presenta anormalidades importantes, por lo que este modelo podría
considerarse bastante simple, ver Figura 6.8.
Las conductividad termal asignada a las lutitas fue bastante alta, entre 2.5 y 2.8 W/mºC, pero
dentro del rango propuesto por varios autores (Reiter y Tovar, 1982; Barker, 1996). Para las arenas se
consideró conductividades entre 2.9 y 3.0 W/mºC. Las velocidades de fluidos asignadas en este modelo
al igual que en el anterior son pequeñas y negativas (x10-12 m/s). En las Tablas 6.4 y 6.4 se resumen los
parámetros considerados en este modelo.
93
El gradiente gotérmico calculado en Maturín Centro es de 20,35 ºC/km, lo cual nos indica que la
zona de Maturín Norte esta más caliente, como es de esperarse por encontrarse en una zona de fallas y
a muy cercana a la Serranía del Interior Oriental. La zona de Maturín Centro en cambio no presenta
elementos tectónicos y/o estratigráficos importantes que pudieran aumentar su gradiente gotérmico.
PARÁMETROS
VALORES CARACTERÍSTICOS
CORTEZA
Espesor
35km
3
Densidad (ρ)
2800 kg/m
Conductividad Termal (k)
3.3 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
H=Ho*exp (-z/h) , Ho=1x10
-10
W/ kg, h=15km
LITOSFERA SUBCORTICAL
Espesor
45km
3
Densidad (ρ)
3300 kg/m
Conductividad Termal (k)
3.5 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
0 W/ kg
MODELO TERMAL
Temperatura superficial ( To)
28.33ºC
Temperatura de la base (Tm)
1400 ºC
Flujo de Calor del Manto (Qm)
40 mW/m
Espaciamiento Vertical (∆z)
Espaciamiento de tiempo (∆t)
Número de Nodos
Extensión Vertical del modelo
2
1000m
-5
5 x10 Ma
78
80km
Tabla 6.4: Parámetros y valores característicos generales en la zona de Maturín Centro.
94
Temperatura (ºC)
0
200
400
600
800
1000
0
28.33ºC
Sedimentos
10
20
Corteza
k=3.3 W/ mºC
3
ρ=2900 kg/m
H=Ho*exp(-z/h)
Profundidad (km)
30
Manto
Litosférico
k=3.5 W/ mºC
3
ρ=3300 kg/m
H=0
1400ºC
40
50
60
70
80
Manto
90
Figura 6.7: Geoterma Litosférica Calculada en Maturín Centro.
1200
1400
1600
95
Temperatura (ºC)
0
20
40
60
80
100
120
140
160
0
k= 2.9
1
k=2.8
Observada
Profundidad (km)
2
k=2.5
Calculada
3
4
5
k= 3.2
6
Corteza
7
Figura 6.8: Curvas Observada y Calculada en Maturín Centro, en sedimentos.
Profundidad (km)
k (W/mºC)
1
2.8
H (W/kg)
3
ρ (kg/m )
V (m/s)
1.0x10
-11
2250
0
2250
0
2
1.85
1.0x10
-10
2
1.85
1.0x10
-10
2250
4
1.85
1.0x10
-10
2250
0
5
3.0
1.0x10
-11
2650
0
6
3.0
1.0x10
-11
2650
0
-5 x10
Tabla 6.4: Parámetros y valores característicos en Maturín Centro, en sedimentos.
-12
180
96
6.4.3 Maturín Oeste
La geoterma litosférica calculada por el algoritmo FDTHERM_1D en Maturín Oeste se presenta
en la Figura 6.9 y los parámetros generales y sedimentarios considerados se encuentran resumidos en
las Tablas 6.5 y 6.6.
Se emplearon conductividades termales entre 1.4 -2.93 W/mºC m para las lutitas y 3.2 W/mºC m
para las arenas. Se introdujo velocidades de fluidos negativas (x10-10 -10-11 m/s) en varios nodos en los
primeros 6 km.
Entre una profundidad de 2.7-4.5 km se registra un aumento de temperatura considerable, el cual
se logro modelar con un aumento de la conductividad termal en ese intervalo de profundidad y la
presencia de fluidos en los bordes de la anomalía, por lo que podría asociarse a la existencia de un
reservorio o acuífero. La Figura 6.10 muestra la curva observada y la calculada.
Hacia la parte más occidental de la Cuenca Oriental de observa un incremento en el gradiente
geotermal (31,72 ºC/km), posiblemente asociado a un entrampamiento de gases (Urbani, 1991), el cual
será discutido con mayor detalle más adelante.
97
PARÁMETROS
VALORES CARACTERÍSTICOS
CORTEZA
Espesor
35km
3
Densidad (ρ)
2800 kg/m
Conductividad Termal (k)
3.3 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
H=Ho*exp (-z/h) , Ho=1x10
-10
W/ kg, h=15km
LITOSFERA SUBCORTICAL
Espesor
45km
3
Densidad (ρ)
3300 kg/m
Conductividad Termal (k)
3.5 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
0 W/ kg
MODELO TERMAL
Temperatura superficial ( To)
28.33ºC
Temperatura de la base (Tm)
1400 ºC
Flujo de Calor del Manto (Qm)
40 mW/m
Espaciamiento Vertical (∆z)
Espaciamiento de tiempo (∆t)
Número de Nodos
Extensión Vertical del modelo
2
300m
-5
5 x10 Ma
266
80km
Tabla 6.5: Parámetros y valores característicos generales en la zona de Maturín Oeste.
98
Temperatura (ºC)
0
200
400
600
800
1000
0
28.33ºC
Sedimentos
10
20
Corteza
k=3.3 W/ mºC
3
ρ=2900 kg/m
H=Ho*exp(-z/h)
Profundidad (km)
30
Manto
Litosférico
k=3.5 W/ mºC
3
ρ=3300 kg/m
H=0
40
50
60
70
80
1400ºC
Manto
90
Figura 6.9: Geoterma Litosférica Calculada en Maturin Oeste.
1200
1400
1600
99
Temperatura (ºC)
0
50
100
150
0
k= 3.2
1
Calculada
Observada
k= 1.7
k= 1.4
k= 2.93
Profundidad (km)
2
3
4
k= 2.14
k=2.14
5
Corteza
6
Figura 6.10: Curvas Observada y Calculada en Maturín Oeste, en sedimentos.
200
100
Profundidad (km)
k (W/mºC)
0.3
3.2
H (W/kg)
3
ρ (kg/m )
V (m/s)
1.0x10
-11
2250
0
2250
0
0
0.6
3.2
1.0x10
-11
0.9
3.2
1.0x10
-11
2250
2250
1.2
1.7
1.0x10
-11
1.5
1.7
1.0x10
-10
2250
0
1.8
1.7
1.0x10
-10
2250
0
2250
0
0
-1.0 x10
-10
2.1
1.7
1.0x10
-10
2.4
1.4
1.0x10
-10
2250
2250
-1.0 x10
-11
-1.0 x10
-11
2.7
2.93
1.0x10
-10
3.0
2.93
1.0x10
-10
2250
3.3
2.93
1.0x10
-10
2250
0
2250
0
0
3.6
2.93
1.0x10
-10
3.9
2.93
1.0x10
-10
2250
2250
4.2
2.14
1.0x10
-10
4.5
2.14
1.0x10
-10
2650
0
4.8
2.14
1.0x10
-10
2650
0
-8.0 x10
-10
Tabla 6.6: Parámetros y valores característicos en Maturín Oeste, en sedimentos.
6.4.4 Guarico
La Figura 6.11 predice la geoterma litosférica para la zona de Guarico, hasta el limite litosferamanto astenosférico, 80 km de profundidad. En este modelo se considero un espesor cortical anómalo
de 25 km, ya que permitió un mejor ajuste de los resultados. En las Talas 6.7 y 6.8 se presentan los
parámetros generales y específicos (sedimentarios) utilizados en este modelo.
Las conductividades termales en estratos lutíticos varían entre 1.24 y 1.8 W/mºC, y en las arenas
se utilizó un valor de 2.5 W/mºC m, relativamente bajo entre de areniscas, pero mayor comparado con las
lutitas.
101
El gradiente geotermal calculado resulto bastante elevado y anormal (45,55ºC/km), mucho mayor
que en los modelos anteriormente estudiados
La geoterma observada presenta un incremento importante de temperatura a una profundidad de
2 km, que se logro modelar considerando una velocidad de fluido mayor (5x10-9 m/s) que las
anteriormente utilizadas, en el límite sedimentos-corteza, ver Figura 6.12.
PARÁMETROS
VALORES CARACTERÍSTICOS
CORTEZA
Espesor
25km
3
Densidad (ρ)
2800 kg/m
Conductividad Termal (k)
3.3 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
H=Ho*exp (-z/h) , Ho=1x10
-10
W/ kg, h=15km
LITOSFERA SUBCORTICAL
Espesor
55km
3
Densidad (ρ)
3300 kg/m
Conductividad Termal (k)
3.5 W/mºC
Calor especifico
Producción de Calor
1300 J / kg ºC
0 W/ kg
MODELO TERMAL
Temperatura superficial ( To)
28.33ºC
Temperatura de la base (Tm)
1400 ºC
Flujo de Calor del Manto (Qm)
40 mW/m
Espaciamiento Vertical (∆z)
Espaciamiento de tiempo (∆t)
Número de Nodos
Extensión Vertical del modelo
2
300m
-5
5 x10 Ma
266
80km
Tabla 6.7: Parámetros y valores característicos generales en la zona de Guarico
102
Temperatura (ºC)
0
26.48ºC
200
400
600
800
1000
0
Sedimentos
10
Corteza
k=3.3 W/mºC
3
ρ=2900 kg/m
H=Ho*exp(-z/h)
20
Manto
Litosférico
k=3.5 W/ mºC
3
ρ=3300 kg/m
H=0
Profundidad (km)
30
40
50
60
70
1400ºC
80
Manto
90
Figura 6.11: Geoterma Litosférica Calculada en Guarico
1200
1400
1600
103
0
Temperatura (ºC)
50
100
150
200
0
k= 1.24
k= 1.74
Observada
1
Profundidad (km)
k= 1.8
k= 1.6
k= 2.5
Calculada
2
3
Corteza
4
Figura 6.12: Curvas Observada y Calculada en Maturín Oeste, en sedimentos.
Profundidad (km)
k (W/mºC)
0.3
1.24
H (W/kg)
3
ρ (kg/m )
V (m/s)
1.0x10
-10
2250
0
2250
0
0
0.6
1.74
1.0x10
-10
0.9
1.74
1.0x10
-10
2250
2250
1.2
1.8
1.0x10
-10
1.5
1.8
1.0x10
-10
2250
0
1.8
1.6
1.0x10
-10
2250
0
2250
0
-3.0 x10
-10
2.1
1.6
1.0x10
-10
2.4
2.5
1.0x10
-11
2650
0
1.0x10
-11
2650
-5.0 x10
2.7
2.5
Tabla 6.8: Parámetros y valores característicos en Guarico, en sedimentos
-9
104
El hecho de que en las regiones de Maturín Oeste y en Guarico se lograron modelar
satisfactoriamente los incrementos abruptos de temperatura en los estratos sedimentarios considerando
un flujo de calor advectivo, podría apoyar la hipótesis de Urbani (1991), la cual propone que los altos
gradientes de temperaturas en la zona norte de Cuenca Oriental de Venezuela, específicamente hacia la
zona occidental (subcuenca de Guarico), están vinculados a un entrampamiento de gases, ya que según
este autor, los grandes yacimientos de gas de esta zona se deben a un proceso compresivo de norte a
sur, que por efecto de compresión adiabática de los fluidos eleva la temperatura en una franja paralela al
frente de montaña, produciendo un aumento del gradiente geotérmico de la región (7 ºC/100m).
Además este modelo en particular presenta arcillas, mineral caracterizado, entre otras cosas, por
baja conductividad termal. Esta capa de arcillas de edad Mioceno podría estar actuando como sello del
gas, entrampándolo, impidiendo el flujo de calor hacia la superficie y haciendo que se concentre bajo
estos sedimentos, aumentando entonces sus valores de temperatura (Fernández, 2004).
Esta hipótesis no es completa del todo, ya que no logra explicar por que cerca del frente de
deformación de la Serranía del Interior no se observa la presencia de grandes volúmenes de gas, como
es de esperarse según esta teoría, ya que el norte de la subcuenca de Maturín también esta asociado al
proceso compresivo de norte a sur (colisión de la Placa Caribe con la Placa Suramericana).
Es importante señalar que tal vez la anomalía termal fue lo que genero o aumento los grandes
volúmenes de gas encontrados en Guarico, y no al contrario como lo propone Urbani (1991). Ya que
posiblemente fueron los elevados gradientes de temperaturas en esa zona lo que contribuyó a cocinar el
petróleo existente en el área.
105
Se puede pensar en la existencia de una característica epirogénica, como una pluma de manto,
directamente bajo el área norte de la Cuenca Oriental de Venezuela que está elevando los gradientes
termales en la zona. Sin embargo, las variaciones de temperatura observadas en profundidad y en
distancia horizontal no apuntan hacia ésta hipótesis (Fernández, 2004).
Aunque se registran aumentos bruscos en la temperatura que podrían estar relacionados a una
fuente tal como una pluma de manto bajo el área de estudio, las isotermas de la Figura 6.13 estarían
concentradas directamente sobre la fuente y los gradientes correspondientes serían más fuertes hacia la
base de la anomalía (o tope de la fuente) para disminuir hacia la superficie.
Este comportamiento no es el observado en las isotermas analizadas por Fernández (2004), lo
que permite pensar que no existe ninguna fuente epirogénica, al menos directamente bajo la Cuenca
oriental de Venezuela, que esté generando las altas temperaturas. Con esto, queda la posibilidad de que
alguna fuente epirogénica lejana hacia el oeste de la zona se encuentre transmitiendo calor de forma
advectiva hasta la Cuenca Oriental de Venezuela, y cuya transmisión disminuye hasta desaparecer al
este de la Cuenca.
106
W
A
0
E
Distancia Horizontal (Km)
0
50
100
150
200
250
300
A'
350
400
-2000
T (ºK)
Profundidad (m)
-1000
-3000
-4000
-5000
-6000
480
470
460
450
440
430
420
410
400
390
380
370
360
350
340
330
320
310
300
290
280
(404.33ºF
206.85ºC)
(314.33ºF
156.85ºC)
(242.33ºF
116.85ºC)
(152.33ºF
66.85ºC)
(14.33ºF
6.85ºC)
Figura 6.13: Sección Termal de un perfil oeste- este en la Cuenca Oriental de Venezuela
Tomado de Fernández (2004)
!
"
La zona de alto flujo de calor es más extensa en Venezuela que el área estudiada. Abarca el
norte del país desde el Estado Falcón al occidente al Estado Sucre al oriente, Figura 6.14, (Hamza y
Muñoz, 1996; Fernández, 2004).
El aumento del gradiente geotérmico en especial en la zona de Guarico podría estar relacionado
al hecho de que el límite corteza-manto litosférico se encuentra 25 km de profundidad, ya que en
cualquier región donde exista un adelgazamiento cortical (i.e. ascenso de manto litosférico más caliente)
o alguna otra fuente calor en la base de la corteza, se tendrá un aumento del gradiente geotérmico.
107
-74.00
-73.00
-72.00
-71.00
-70.00
-69.00
-68.00
-67.00
-66.00
-65.00
-64.00
-63.00
-62.00
-61.00
-60.00
-59.00
13.00
13.00
12.00
12.00
100
85
11.00
11.00
10.00
10.00
9.00
9.00
8.00
8.00
7.00
7.00
80
75
70
65
60
55
50
45
40
35
Estación de Medición
de Flujo de Calor
100 Km
6.00
-74.00
-73.00
-72.00
-71.00
-70.00
-69.00
-68.00
-67.00
-66.00
-65.00
-64.00
-63.00
-62.00
-61.00
-60.00
25
20
6.00
-59.00
Figura 6.14: Flujo de Calor para Venezuela. Modificado de Hamza y Muñoz (1996)
Otros estudios en la zona central de Venezuela (Estado Guárico) han planteado un
adelgazamiento cortical (Ughi, 2002; Márquez, 2003), basados en modelos gravimétricos. Pero los
estudios de reflexión de sísmica profunda en esta área (Vieira, 2005) no han revelado la existencia de
dicho adelgazamiento. Hacia el nor-occidente (Estado Falcón) varios estudios también proponen un
adelgazamiento cortical, basados en consideraciones tectónicas (Audemar, 1993), presencia intrusiones
basálticas (Muessig, 1978; Muessig, 1984), modelado gravimétrico (Rodríguez y Sousa, 2004) y sísmica
profunda (Bezada, 2005). Posiblemente este adelgazamiento pudiera extenderse hacia la zona central
del país, elevando significativamente los valores de temperatura.
La idea básica para esta hipótesis es que la subducción de la Placa Caribe bajo la Placa Sur
Americana (Van der Hilst y Mann, 1994; Bezada (2005), podría estar relacionada con un adelgazamiento
cortical en el Estado Falcón (Bezada, 2005) y posiblemente en el Estado Guarico, lo que estaría elevando
los valores de temperaturas, especialmente en el área de estudio.
30
0
108
A través de la técnica de retro-evolución o backstripping (basada en isostacia tipo Airy, 1D) se
logró reconstruir la historia de subsidencia de cuatro regiones representativas de la Cuenca Oriental de
Venezuela, desde el Cretácico hasta el Presente.
En base a este análisis de subsidencia se identifico las tectonosecuencias de Margen Pasivo y
Margen Activo propuestas por varios autores (González de Juana, 1980; Erlich y Barrett, 1990; entre
otros). La subsidencia es diacrónica y más joven en este que en el oeste de la Cuenca Oriental.
Las tasas de subsidencia más bajas oscilaron entre 9.7 - 44.03 m/Ma (Margen Pasivo) y las más
altas entre 56.32-706.5 m/Ma (Margen Activo).
El modelo de subsidencia obtenido en Guarico presento un levantamiento o rebote isostático, de
edad Oligoceno (28Ma), que podría estar asociado al evento termal propuesto por Pérez de Armas
(2005). Este levantamiento también podría estar vinculado al desarrollo o reactivación de fallas normales
propuesto por dicho autor en ese tiempo.
Los modelos termales (1D) generados en esta investigación demuestran que la teoría de
modelado numérico termal es capaz de reproducir el comportamiento termal o geoterma de una región.
Los gradientes geotérmicos estimados en las regiones estudiadas, confirmaron que hacia el
oeste de la Cuenca Oriental existe un aumento significativo de temperatura.
Las conductividades termales utilizadas en el modelado termal oscilaron entre 1.2 y 2.8 W/mºC
(lutitas) y entre 2.9-3.2 W/mºC (areniscas). En la corteza se consideró 3.3 W/mºC y en el manto 3.5
W/mºC.
108
109
Velocidades de fluidos en estratos sedimentarios permitieron el ajuste de las geotermas
observadas y calculadas. En los modelos generados en Maturín Norte, Maturín Centro y Maturín Oeste
se utilizaron valores pequeños de velocidad (x10-12 - x10-10 m/s), en cambio en Guarico fue necesario
incrementar el valor a 5.0x10-9 m/s a 2700 m de profundidad, para reproducir la anomalía termal de esa
zona. Por esto se asocia la anomalía termal de Guarico con un proceso compresivo norte-sur, que por
efecto de compresión adiabática de los fluidos eleva la temperatura en una franja paralela al frente de
montaña, produciendo un aumento del gradiente geotérmico de la región, hipótesis planteada por Urbani
(1991). Es importante señalar que esta hipótesis no logra explicar por que en el frente de deformación de
la Serranía del Interior no existen grandes volúmenes de gas como en Guarico, ya que esta área también
esta asociada al proceso compresivo norte a sur.
El límite corteza-manto que mejor ajustó las geotermas observadas en Maturín Norte, Maturín
Centro, Maturín Oeste y Guarico fue 40 km, 35 km, 35km y 25 km, respectivamente. Hacia la zona más
nor-occidental de Venezuela (Estado Falcón) se ha propuesto un episodio incipiente de adelgazamiento
cortical (Bezada, 2005) a partir de sísmica profunda, que pudiera extenderse hacia la zona central de
Venezuela. De ser cierto esto, este ascenso del manto caliente podría ser el causante principal del
aumento de temperatura en el área de Guarico.
110
Como recomendaciones finales de este trabajo se proponen:
1) A partir de los modelos termales generados en este trabajo reconstruir la evolución termal de cada uno
de ellos, para identificar las etapas termales ocurridas en cada modelo y su posible relación con la
anomalía termal presente en Guarico.
2) Desarrollar modelos termales y de subsidencia similares o en 2D en otras regiones de Cuenca
Oriental, con fin de que puedan correlacionarse y así obtener un modelo que explique regionalmente la
evolución termal y tectónica del área.
3) Controlar y refinar los modelos utilizando mayor densidad de pozos con información hasta el
basamento, datos de porosidad, edades (a partir de bioestratigrafía o magnetoestratigrafía)
conductividades termales.
4) Emplear información gravimétrica, sismológica y aeromagnética como soporte.
y
111
Airy, G., 1855. “On the computation of the effect of the attraction of mountain masses as disturbing the
apparent astronomical latitude of stations of geodetic surveys”. Phil. Trans. R. Soc. Volumen 145. p: 101104.
Allen, P. A., Allen J.R., 1990. “Basin Analysis Principles & Applications”. Blackwell Science. 451 p.
Andrews-Speed, C.P., Oxburgh, E.R., y Cooper, B.A., 1984, “Temperature and depth-dependent heat
flow in western North Sea”. AAPG Bull. 68 (11). p:1764-1781.
Athy, L.F., 1930, “Density and compactation of sedimentary rocks”. Am. Assoc. Petroleum Geologists
Bull. v.14, no 1, p: 1-24.
Audemar, Fr., 1993, “Neotectonique, sismotectonique et aléa sismique du nord-ouest du Vénezuela
(systéne de failles d´Oca-Ancón) ” . Tesis Doctoral, Universidad de Montpellier II. 369p.
Ávila, J., 2005, Modelo Bidimensional de la Corteza en la Zona de Colisión Caribe-Suramérica, Región
Oriental de Venezuela (Estado Anzoátegui). Trabajo de Grado. Universidad Simón Bolívar. Caracas,
Venezuela.
Aymard, R., Pimentel, L., Eitz, P., Chaouch, A., Navarro, J., Mijares, J. y Pereira, J., 1990.
“Geological Integration and Evaluation of Northern Monagas, Eastern Venezuelan Basin” en J. Brooks,
ed., Classic petroleum provinces. Geological Society of London Special Publication # 50. p: 37-53.
Banks, R., Parker, R. y Huestis, S., 1977. “Isostatic compensation on a continental scale: Local versus
regional mechanisms”. Geophys. J. Roy. astr. Soc. 51. p: 431-452.
Banks, L. M., y Driver, S.E., 1957, “Geologic history of Santa Ana structure, Anaco structural trend,
Anzoátegui, Venezuela”. American Association of Petroleum Geologists Bulletin, Tulsa, OK, United
States. vol. 41 (2). p: 308-325.
Barrell, J., 1914. “The strength of the earth's crust, 6”. J. Geol. Volumen 22. p: 441-468; 655-683.
Bartok, P., 1993, “Prebreackup geology of the Gulf Mexico-Caribbean: Its relation to Jurasic and Triassic
rift system of the refion”. Tectonics, Vol. 12, p: 441-459.
Beaumont, C.,1981. “Foreland Basins ”.Geophys.J.R.. 65. p: 291 –329.
Beck, C. 1983, “Essai sur l´évolution géodynamiquedes Caraibes sud-orientales”. Bull. Soc. Geol. Fr. 7
(XXV). p: 169-183.
112
Beccaluva, L., Coltorti, M., Giunta, G., Iturralde-Vienent, M., Navarro, E., Siena, F., Urbani F., 1996.
“Cross-sections through the ophiolitic units of the southern and northern margins of the Caribbean Plate in
Venezuela (northern Cordillera) and Central Cuba”. Ofioliti 21, 85-103.
Bellizzia, A., 1986, Sistema Montañoso del Caribe, una cordillera alóctona en la parte norte de América
del Sur: VI Congreso Geológico Venezolano, 10, 6657-6836. 58
Bell, J.S., 1970, “Tectonic Evolution of the Central Part of the Venezuelan Coast Ranges”, Memoria 130,
Geological Society of America, p. 107-118.
Beardsmore, G.R. y Cull, J.P., 2001, “Crustal Heat Flow. A guide to Measurement and Modelling”.
Cambridge University press.
Bezada, M., 2005, Modelo Bidimensional de la Corteza en la Zona de Colisión Caribe-Suramérica,
Región Occidental de Venezuela (Estados Falcón y Lara). Trabajo de Grado. Universidad Simón Bolívar.
Caracas, Venezuela.
Blanco, B., Gómez, E., y Sánchez, H., 1998, Evolución tectónico-sedimentaria del norte de los estados
Anzoategui, Guarico, Cojedes y Portuguesa. IV Congreso Venezolano de Geofísica, p:151-157.
Bond, G. y Kominz, M., 1984, “Construction of Tectonics Subsidence of The Early Paleozoic
Miogeocline, Southern Canadian Rocky Mountains: Implications for Subsidence Mechanisms, age of
Breakup, and Crustal Thining” . G.S.A. Bull. 95, (2): 155 – 173.
Bott., M.H.P., 1979, “Subsidence mechanisms at passive continental margins”. Mem. Am. Ass. Petrol.
Geol. vol 29. p:3-9.
Bradley, D.C., and Kidd, W.S.F., 1991, “Flexural Extension of the Upper Continental Crust in Collisional
Foredeeps”. Geological Society of America Bulletin, v. 103, p.1416-1438.
Choppin, H., Gonzáles, A. Rodriguez, H. Roux, E. y Uzcategui, M.,1989.Síntesis estratigrafica y
tectónica de Anzoategui y Guárico Este. SETAGE. Tomo II Geofísica. Corpoven. Informe Interno.
Carballo, A., 2004. “Modelo Geodinámico Integrado de la Subcuenca de Guárico y la Cordillera Central
Venezolana en el Estado Guárico”. Universidad Simón Bolívar. Caracas. Venezuela. (Tesis de Pregrado).
Cepet, 1989, “La Industria Venezolana de los Hidrocarburos”. Tomo I. Centro de Formación y
Adiestramiento de Petróleos de Venezuela y sus empresas filiales. Caracas. p: 61-261.
113
Colmenares, L.B.,y Zoback, M.B.,2001, Regional stress field and sismotectonics of northern of
Venezuela. Standford University. XI Congreso Venezolano de Geofísica, SOVG.
Daal, J., y Lander, R., 1993, “Yucal-El Placer Field, Venezuela, Eastern Venezuela basin, Guarico basin”,
en Foster, N.H, y Beamount, E.A., eds., American Association of Petroleum Geologist Teatrise: Structural
Traps VIII, p.307-328.
Demets, C., Gordon, R.G., Argus, D.F. And Stein, S., 1994. “Effects of recent revisions to the
geomagnetic time scale on estimates of current plate motions”. Geophysical Research Letters, n.21, p.
2191-2194
Di Croce, J., 1999.Eastern Venezuelan Basin: Sequence Stratigraphy and Structural Evolution. Trabajo
de Ascenso, Universidad Central Venezuela.
Di Croce, J. 1995. “Eastern Venezuelan Basin: Sequence Stratigraphy and Structural Evolution”,
Ph.D. dissertation. Universidad de Rice, Houston, Texas. 225 p.
Dickinson, W. 1974. “Plate tectonics and sedimentation” en W.R. Dickinson (ed.) Tectonics and
Sedimentation. Spec. Publ. Soc. econ. Paleont. Miner. Tulsa, 22. p: 1-27.
Diebold, J., Stoffa P., Buhl P. y Truchan M.,1981,” Venezuelan basin crustal estructure”, Journal of
Geophysical Research, Vol. 86, B9: 7901 – 7923.
Dewey, J., 1981, “Apuntes del Curso de Geotectónica de Jonh Dewey s.p.i”. Inédito.
Earle, S., 2004, “Types of the sedimentary basins”. Malaspina University-College. Página actual:
http://web.mala.bc.ca/earle/geol201/basin-types.htm
Edgar, N., Ewing J. y Hennion J, 1971, “Seismic refraction and reflection in Caribbean Sea”. American
Association of Petroleum Geologists Bulletin, 55: 833 – 870.
Erlich, R.N. y Barrett, S.F. 1992. “Petroleum Geology of the Eastern Venezuela Foreland Basin” en
Macqueen, R. W., y Leckie, D. A., eds., Foreland Basins and Fold Belts. AAPG Memoria 55. p: 341-362.
Erlich, R.N. y Barrett, S.F., 1990, Petroleum Geology of the Eastern Venezuela Foreland Basin. Amoco
Production Company, Houston, Texas, USA.
Falvey,D.,1974. “The Development of Continental Margins in Plate Tectonics Theory”. Australian. Petrol.
Explo.Assoc.Jour.,Sidney 14. p:95-106
114
Erikson, J., 1992, “Northeastern Venezuelan´s Jurassic through Eocene pasive margin, Hispaniola´s
Neogene Cibao Basin, and their histories and causes of evolution”. (Ph.D. thesis): Hanover, New
Hampshire, Dartmounth College, 472p.
Erikson, J. y Pindell, J., 1993, “Analysis of subsidence in northeastern Venezuela as a discriminator of
tectonic models for northern South America”. Geology. v.21. p: 945-948.
Fasola, A.,Giffuni, G., Crespo, S., Paredes, I. Y Euribe, A., 1998, Estudios bioestratigráficos del
intervalo Cretácico Superior (Maestrichtiense) a Mioceno Inferior en el norte del Estado Guarico,
Venezuela. VI Congreso Geológico Venezolano. Memorias, v.I, p: 588-645.
Feo-Codecido, G., Smith, F.D., Jr., Alboud, N., y Di Giacomo, E., 1984, “Basament and Paleozoic
rocks of the Venezuelan Llanos basin”, en Bonini, W.E., Hargraves, R.B., y Shagan, R., eds. The
Caribbean-South American plate boundary and regional tectonics: Geological Society of American Memoir
162, p.213-216.
Fernández, D, 2004, Análisis de la Cuenca Oriental de Venezuela a partir de información de pozos, Tesis
de Grado. Universidad Simón Bolívar. Caracas, Venezuela.
Fowler, C.M.R, 1990, “The Solid Earth”. Cambridge University Press, USA.
Gallagher, K., 1989, “An examination of some uncertainties associated with estimates of sedimentation
rates and tectonic subsidence”. Basin Research, v.2, p: 97-114.
García, D., 1998. “Desarrollo de modelos numéricos de flexión litosférica: aplicación a fosas oceánicas y
cuencas
de
antepaís”.
Barcelona.
España.
(Tesis
Doctoral).
Pagina
web
actual:
http://www.geo.vu.nl/~gard/papers/thesis
Giunta, G., Beccaluva, L., Colorti, M. y Siena, F., 1997. “Ophiolitic units of the southern margin of the
Caribbean Plate in Venezuela: a rapprasail of their petrogenesis and original tectonic setting”. Sociedad
Venezolana de Geólogos. VIII Congreso Geológico Venezolano. Tomo 1. p: 331-337.
Giunta, G., Beccaluva, L., Colorti, M., Siena, F. y Vaccaro, C. 2002, “The southern margin of the
Caribbean Plate in Venezuela: tectono-magmatic setting of the ophiolitic units and kinematic evolution”.
Lithos 876 (en impresión).
Giunta, G., Marroni, M., Padoa, E. y Pandolfi, L., 2003. “Geological Constraints for the Geodynamic
Evolution of the Southern Margin of the Caribbean Plate” en C. Bartolini, R. T. Buffler, y J. Blickwede,
115
eds., The Circum-Gulf of Mexico and the Caribbean: Hydrocarbon habitats, basin formation, and plate
tectonics: AAPG Memoria 79. p: 104-125.
González de Juana, C., Iturralde, J. y Picard, X. 1980. “Geología de Venezuela y de sus Cuencas
Petrolíferas”. Volumen I y II. Ediciones FONINVES. Caracas. Venezuela.
Haack, S. C., 1987, “A thermal model of the sailback pelycosaur”. Paleobiology 12: 450-458.
Hamblin, W. y Christiansen, E.,1998, “Earths Dynamic Systems”, 8th edition,Prentice-Hall. 601p.
Hamza, V.M. y Muñoz, M., 1996, “Heat flow map of South America”. Geothermics, 6, 599-646,
Haq, B., Handerbol, J. y Vail, P.R., 1987, “Chronology of fluctuacting sea levels since the Triassic (250
million years ago to present)”. Science, v.235, no 4793, p: 1156-1167.
Haxby, W., Turcotte,D., y Bird, J., 1976. “Thermal and Mechanical Evolution of the Michigan Basin”.
Tectonophysics. Amsterdan 36 (1-3).p:57-75
Houtz, R. y W. Ludwig, 1977, “Structure of the Colombia Basin, Caribbean Sea, from profiler sonobuoy
measurements”. Journal of Geophysical Research, 82: 4861 – 4867.
Hung, E., 1997, “Foredeep and thrust belt interpretation of the Maturin subbasin, Eastern Venezuela
basin”. (M.A Dissertation): Houston, Rice University, 125 p.
Jácome, M.I, 2001, The formation of the Monagas Foreland Basin, Venezuela. University of Liverpool
(Tesis doctoral), Liverpool, UK, p. 204
Jácome, M., N. Kusznir, F. Audemard y S. Flint, 2003, “Tectono-stratigraphic Evolution of the Maturin
Foreland Basin: Eastern Venezuela”. En: C. Bartolini, R. Buflfer y J. Blickwede (Eds.), The Circum-Gulf of
Mexico and the Caribbean: Hydrocarbon habitats, basin formation, and plate tectonics, AAPG Memoir,
79: 735-749.
Jarvis G. y Mckenzie
D. ,1980. “Sedimentary Basin Formation with Finite Extension Rates.” Earth
Planet. Sci. Lett., Amsterdam, p: 42-52.
Jordan, T. ,1975, “The present – day motion of the Caribbean Plate”. Journal of Geophysical Research,
80: 4433 – 4439.
Kingston D., Dishroon C. y Williams P.,1983, “Global basin classification”. Bull. Am. Assoc. petrol.
Geol., 67: 2175 – 2193.
116
Kominz, M. y Bond,G., 1986, “Geophysical Modelling of the thermal History of Foreland basin”. Nature.,
London. p 320.
Kiser, G.D, 1997, Formación La Pascua; Eoceno Tardío-Oligoceno temprano, Estados Guarico:
PDVSA(Petróleos
de
Venezuela)Intevep,
Código
Geológico
de
Venezuela,
www.pdv.com/lexico/126w.htm
Ladd, J. y Watkins J.,1980, “Seismic stratigraphy of the Western Venezuela Basin”, Marine Geology, 35:
21 – 41.
Lambertini, R., García, L., FLAR, P., González, C., Azpiritxaga, I., 1987. Litofacies, Ambientes
Sedimentarios y Diagénesis en las Areniscas del terciario del Noreste del Estado Guárico (Infirme
Técnico). PDVSA-Intevep, 133p.
Lemos, C.,1997, “FDTHERM: A Fortran 77 solver for 2D low-speed flows with bouyancy effects”.
Computer and Geosciences, vol. 23, No. 2, p:139-151.
Le Pichon, W. y Sibuet, J.C., 1981, “Passive margin : a model of formation”. J. Geophys. Res, 86. p:
3708-3720.
Lowrie, W., 1997, “Fundamentals of Geophysics” . Cambridge University Press. New York.
Lugo, J. y Mann, P., 1995, “Jurassic-Eocene tectonic evolution of Maracaibo Basin, Venezuela”, en
Tankard, A., Suárez, R., y Welsink, H. J., eds., Petroleum Basins of South America: American Association
of Petroleum Geologists Memoir 62, p: 699-725.
Maceda, R., 2005, “The western end of the Serranía del Interior, Venezuela: A review”. 6th International
Symposium on Andean Geodynamics (ISAG 2005, Barcelona), Extended Abstracts:468-471.
Mckenzie, D.P., 1978, “Some remarks on the development of sedimentary basins”. Earth Planet. Sci. Lett
40.
Mcnutt, M. y Menard, H., 1982. “Constraints on yield strength in the oceanic lithosphere derived from
observations of flexure”. Geophys. J. Roy. astr. Soc., 71. p: 363-394.
Márquez, E., 2003, Evolución Tectono-Termal desde el Paleozoico hasta el Reciente en un sector de la
sub-cuenca de Guárico, estados Guárico y Anzoátegui, Venezuela. Universidad Central de Venezuela
(Tesis Doctoral ). Caracas, Venezuela.
117
Méndez, O., 1985, Historia Geológica graficada de la Cuenca Oriental de Venezuela. VI Congreso
Geológico Venezolano, Memoria Tomo II, Sociedad Venezolana de Geólogos, Caracas, Venezuela, p.
1000-1040.
Miall, A.D., 1984, “Principles of sedimentary basin analysis”. New York, Springer-Verlag.
Mooney, W.,1980, “An East Pacific - Caribbean ridge during the Jurassic and Cretaceous and the
evolution of western Colombia”, Houston Geological Society Continuing Education Series, School of
Geoscience, Louisiana State University, Baton Rouge, La., 55 – 74.
Moticska, P., 1985, “ Volcanismo Mesozoico
en el Subsuelo de la Faja petrolífera del Orinoco”. VI
Congreso Geológico Venezolano. p. :1929-1938.
Muessig, K. W., 1978. “The central Falcón igneous suite, Venezuela: alkaline basaltic intrusions of
Oligocene-Miocene age”. Geol. en Mijin. 57(2): 261-266.
Muessig, K. W., 1978. “Structure and Cenozoic tectonics of the Falcon Basin, Venezuela, and adjacent
areas”. The Caribbean-South American plate boundary and regional tectonics; Memoir - Geological
Society of America, 162, p. 217-230.
Mussett A.E. & Khan A., 2000. “An Introduction to Geological Geophysics”. Cambridge. Univ. Press, p :
269 – 283.
Navarro, E. 1983, Petrología y petrogénesis de las rocas metavolcánicas del Grupo Villa de Cura”. GEOS
N° 28 (Caracas, Escuela de Geología y Minas, Universidad Central de Venezuela). p: 170–317.
Officer, C., Ewing J., Hennion J., Harkinder D. y Miller D. ,1959, “Geophysical investigations in the
eastern Caribbean – Summary of the 1955 and 1956 cruises, in Ahrens”, Physics and Chemistry of the
Earth, Pergamon, New York, 3: 17 – 109.
Ostos, M., 1990, “Evolución Tectónica del margen Sur-Central del Caribe basado en datos geoquímicos”.
GEOS N° 30 (Caracas, Escuela de Geología y Minas, Universidad Central de Venezuela). p: 1-294.
Parnaud, F., Gou, Y., P., J.C, Truskowski, I., Gallango, O. y Passalacqua, H., 1995, “Petroleum
geology of the central part of the eastern Venezuelan Basin”. Petroleum basins of South America, AAPG.
Memoir 62, p.741-756. American Association of Petroleum Geologists, Tulsa.
118
Pennington, W.,1981, “Subduction of the eastern Panama Basin and Seismotectonics of northwestern
South America”. Journal of Geophysical Research, 86: 10753 – 10770.
Pérez de Armas, J., 2005,”Tectonic and termal history of the western Serranía del Interior foreland fold
and thrust belt and Guárico basin, north-central Venezuela: Implications of new apatite fission- track
analysis and seismic interpretation”. Venezuela: Geological Society of America. Special paper 394, p:271314.
PDVSA-Intevep, 1997, III Léxico estratigráfico de Venezuela. http//:pdv.com/léxico
Pindell, J.,1993, “Mesozoic – Cenozoic Tectonic and Stratigraphy Development of the eastern Caribbean
and northern South America, Implications for eastern Venezuela”. Informe interno de PDVSA. EPC 10462.
Pindell, J. y Barrett, S. 1990, “Geological evolution of the Caribbean Region: a Plate-tectonic
prospective” en Dengo, G., Case, J. (Eds.), The Geology of North America, Volumen H. The Caribbean
Region. G. S. A. p: 405-432.
Pindell, J. and Dewey, J., 1991,“Permo-Trasic Reconstructions of Western Pangea and Evolution of the
Gulf of Mexico/Caribbean Region”. Tectonic 1. p:179-211.
Pindell, J. y Kennan, L., 2001a, “Kinematic Evolution of the Gulf of Mexico and Caribbean”. Página web
actual: http://tectonicanalysis.com/site/download/papercarib01.pdf.
Pindell J. y Kennan, L., 2001b, “Processes and Events in the Terrane Assembly of Trinidad and
Eastern Venezuela”. Página web actual: http://tectonicanalysis.com/download/papertrin01.pdf
Pratt, J., 1855. “On the attraction of the Himalaya Mountains and of the elevated regions beyond them,
upon the plumb line in India”. Phil. Trans. R. Soc. Volumen 145. p: 53-100.
Renaut, W. y Ashley, G., 2002, “Sedimentation in continential rifts”. SEPM (society for sedimentary
geology) special publication No.73. En: http://www.geosci.usyd.edu.au/users/prey/Teaching/Geos3003/EReports/eR.2003/GroupD/Report2/web%20pages/contents.html
Robert, P., 1988, “Organic metamorphism and geothermal history: microscopic study of organic matter
and thermal evolution of sedimentary basins”. Norwell, MA, Kluwer Academic Publishers, 311.
Rodríguez, J., Sousa, J.C., 2004, Modelado Geológico –Geofísico a Través de la Cuenda de Falcón.
Trabajo de Grado, Universidad Central de Venezuela.
Rondón, K., 2004, Modelo geodinámico integrado de la Subcuenca de Guárico y la Cordillera de la
Costa en el Estado Anzoátegui, Tesis de Grado. Universidad Simón Bolívar. Caracas, Venezuela.
119
Royden, L., Sclater, G., Von Herzen, R., 1980. ”Continental Margin Subsidence and Heat Flow”.
Important parameters in Formation of Petroleum Hydrocarbons. A.A.P.G. Bull.,Tulsa,Okla 64. p:173-187.
Ruby, W.W. y Hubbert, M.K., 1960, “Role of fluids pressure in mechanics overthrust faulting. II,
Overthrust belt in geosynclinal area western Wyoming in ligth of fluid-pressure hypothesis”. Geological
Society of America Bulletin, v.60, p:167-205.
Rybach L., 1976, “Radioactive heat production: A physical property determined by the chemistry of
rocks”. In: R.G.J. Strens (ed.): "The Physics and Chemistry of Minerals and Rocks", Wiley & Sons, London
309-318.
Rybach L., Cermák V., 1982, “Radioactive heat generation in rocks”. In: G. Angenheister (ed.): "Landolt
& Börnstein V/1: Physical Properties of Rocks", 353-371, Springer Verlag, Heidelberg-Berlin-New York.
Rybach L., 1986, “Amount and significance of radioactive heat sources in sediments”, In: "Thermal
Modeling in Sedimentary Basins", J. Burrus (ed.); Editions TECHNIP Paris, 311-322.
Sawyer, D., Hsui, A. y Toksonz,M., 1987, “Extensión, Subsidence and Thermal Evolution of the Angeles
Basin a two Dimensional Model”. Tectonophysics. Amsterdan 133. p:15-32.
Santiago, N., Duerto, L., Olivares, C., Rojas, S., 2004, “Eocene? Oligocene forebulge Migration in
Central Venezuela”. GAC/MAC, St. Catherines, Poster
Sclater, J.G., y Christie, P., 1980, “Continental Stretching: An Explanation of the Post-Mid-Cretaceus
subsidence of the central north sea basin”. Journal of the Geophysical Research, vol. 85, No. B7. p:37113739
Schubert, C. ,1988, “Neotectonics of the La Victoria fault zone, north central Venezuela”, Anales
Tectinicae, 2: 58 – 66.
Sleep, N., 1971, “Thermal Effects of the Formation of Atlantic Continental Margin by Continental
Breackup”. Geophys. Jour. Royal. Astron. Soc., Oxford 24.p : 325-350.
Sleep, N., Nuun, J., & Chou, L., 1980, “Platform basins”. Ann. Rev. Earth Planet. Sci., 8. p:17-34.
Speed, R.C., 1985, “Cenozoic collision of the Lesser Antilles arc and continental South American and
origin of the Pilar fault”. Tectonics, v 4. p: 41-49.
Soto, I., 2000, “Teaching Materials: Cinturones Orogénicos”. Granada, España. Página web actual:
http://www.ugr.es/~geopeta/Teaching.htm
120
Steckler M. y Watts A., 1978, ”Subsidence of the Atlantic –type Continental Margin of New York. Earth
Planet Sci.lett., Amsterdan 41.p:1-13.
Stockmal, G., 1986, “Geodynamic Models of Convergent Margin Tectonics: Transition from Rifted Margin
to Overthrust Belt and Consequences for Foreland-Basin Development”. AAPG Bulletin 20. p: 181-198
Summa, L.L., Goodman, E.D., Richarson, M., Norton, I.O., y Green, A.R., 2003, “Hidrocarbon system
of northeastern Venezuela: Plate through molecular scale-analysis of the genesis and evolution of the
Eastern Venezuela basin”. Marine and Petroleum Geology. v.20, p.323-349, doi:10.1016/so2648172(03)00040-0.
Sykes, L., W. McCann y A. Kafka ,1982, “Motion of the Caribbean plate during the last 7 million years
and implications for earlier Cenozoic movements”, Journal of Geophysical Research, 87:10656 – 10676.
Tearpock, D. y otros, 1998, “Stratigraphic interpretation and prospects for East Guarico study area,
eastern Venezuela Basin”. Subsurface Consultans an Associates, LLC. Houston, Texas. Vol 1. 108p.
Turcotte, D., Mcadoo, D. y Caldwell, J., 1978. “An elastic-perfectly plastic analysis of the bending of the
lithosphere at a trench”. Tectonophysics. Volumen 47. p: 193-205.
Turcotte, D., 1980, “Models for the evolution of sedimentary basin”, en Dynamics of Plate Interiors. pp 2126. Geodynamics Series 1, American Geophysical Union. Washington, D.C.
Turcotte, D. y Schubert, G., 2002, “Geodynamics”. Cambridge University Press, Cambridge, UK.
Ughi, B., 2002, Modelaje Geofísico Integrado de la región central de Venezuela por medio del análisis de
flexión de placas en la sección 67º 00” 0’ W. Trabajo de Grado, Universidad Central de Venezuela
Urbani, F., 1991, Geotermia en Venezuela, Geos. Univ. Central de Venezuela. Caracas, (31): 1-347.
Vail, P., Mitchum, R. y Thompson, S., 1977.”Seismic Stratigraphy and Global Sea Level”. Part 4,
American Association of Petroleum Geologists. Memoir 26. p:83-97
Van der Hilst, R.D., and Mann, P., 1994, “Tectonic implications of tomographic images of subducted
lithosphere beneath northwestern South America”. Geology. v. 22, p. 451-454.
Vieira, E., 2005, Modelo Bidimensional de la Corteza en la Zona de Colisión Caribe-Suramérica, Región
Central de Venezuela (Estado Aragua y Guarico). Trabajo de Grado. Universidad Simón Bolívar. Caracas,
Venezuela.
121
Yoris, F. y Ostos, M., 1997, Geología de Venezuela, Capitulo I, Well Evaluation Conference Venezuela
(WEC). Schlumberger
Watts, A. y Ryan, B., 1976, “Flexure of The Lithosphere and Continental Margin Basins”.
Tectonophysics, Amsterdam. v.36. p: 25 – 44.
Watts, A., Karner, G. y Steckler, M., 1982. “Lithospheric flexure and the evolution of sedimentary
basins”. Phil. Trans. R. Soc., A 305. p: 249-281.
Westbrook, G.K. y Mccann, W.R., 1986, “Subduction of Atlantic Lithosphere beneath the Caribbean, in
Vogt, P.R and Tucholke”, B.E., (eds.): The Western North American Region: Boulder Colorado. Geological
Society of America, The Geology of North America, Boulder, Colorado.
122
FDTHERM
FDTHERM es un algoritmo computacional compilado en FORTRAN 77, para el calculo de flujos
2D con transferencia de calor y de masa basado en la Aproximación de Boussinesq. En este trabajo se
modifico el programa original a una sola dimensión (1D), FDTHERM_1D, estos cambios no afectaron
significativamente la lógica del programa, ni las ecuaciones involucradas. El sistema computacional fue
diseñado para operar en 386,486 o un PC Pentium, usando un compilador de FORTRAN de 32bit. Sin
embargo, el programa también puede ser usado en otras plataformas. El código original esta disponible al
publico en internet desde el servidor IAMG.ORG.
Este algoritmo puede ser usado en el estudio de muchos problemas de práctica importancia,
como el desarrollo de plumas de manto, levantamientos termales, corrientes de densidad, circulación de
lagos y fenómenos de convección de doble difusión.
En muchos flujos de baja velocidad, la variación de las propiedades del fluido con excepción de la
densidad pueden ser ignoradas, y las desviaciones de ρ con respecto a una distribución isentropica de
referencia también puede ser no considerada, menos el término de equilibrio. Si las dimensiones del
sistema estudiado son mucho más pequeñas que la escala de altura de la presión isotermal y la
distribución de temperatura adiabática, entonces la aproximación de Boussinesq se podría aplicar
directamente (Turner (1973) y Tritton (1977) ), es decir, el fluido puede ser tratado como incomprensible,
siempre y cuando la densidad no sea uniforme (Lemos,1997).
4.2.1 Aproximación de Boussinesq
En esta aproximación las ecuaciones que describen el movimiento de un fluido en el cual la densidad
depende principalmente de la Temperatura T, puede ser establecido como sigue: hallando u(x,t), p(x,t) y
T(x,t) para todo x
Ω ' ≡ Ω + ∂Ω para t>0, tal que:
∂u
ρ
+ ∇.(u ⊗ u − v∇u ) + ∇p =
g (1)
∂t
ρo
123
∇.u = 0 (2)
∂T
v
+ ∇. uT −
∇T = 0 (3)
σT
∂t
donde Ω es el dominio del fluido; ∂Ω es el borde de Ω (suavizado); t es el tiempo; u es la
velocidad; p es la presión dividida por la densidad de referencia; T es la temperatura; g es la aceleración
de gravedad;
ρ es la densidad; ρ o
es la densidad de referencia (constante);
σ T es el número de
Prandtl; ∇ = (∂ / ∂x, ∂ / ∂y ) y ⊗ denota el producto de un tensor. Las ecuaciones antes descritas deben
ser complementadas por apropiadas condiciones de bordes para T y v ,en caso de que esta ultima no
se considere constante (Lemos, 1997).
En sistemas físicos de importancia práctica, las condiciones de bordes para T pueden ser de tipo
Dirichlet, Neumann o mixtas, es decir:
T = Tb ( z , t )
− κT
− κT
donde la
κ T es
∂T
= qo (z, t )
∂n
∀z ∈ TDT
∀z ∈ TNT
∂T
= hb ( z , t )(T − Tb ( z , t ))
∂n
la conductividad termal,
(4)
(5)
∀z ∈ TRT (6)
∂Ω = TDT + TNT + TRT , qb y hb son funciones dadas. Estas
condiciones de bordes pueden ser usadas para imponer un valor fijo de Temperatura, Flujo de Calor o
Flujo de Calor Convectivo, respectivamente, en diferentes partes de ∂Ω . Un borde termalmente aislado
corresponde a q b ( z , t ) = 0 , o
∂T
= 0 . (Lemos, 1997).
∂n
La principal dificultad asociada con la solución numérica de las ecuaciones (1), (2) y (3) es la
ausencia de una ecuación de evolución de para p. El gradiente de presión esta en permanente equilibrio
124
con el campo de velocidad, así que la conservación de la masa se cumple siempre. La condición inicial
To (z ) = T ( z ,0 ) especifican el estado inicial del sistema (Lemos, 1997).
Condiciones Iniciales y de Bordes
Para completar la especificación del esquema numérico, se discretizan las condiciones iniciales y
de bordes. La condición inicial de v y T debe ser lo suficientemente regulares, además v debe ser
continua en los bordes (Lemos, 1997).
Las condiciones de bordes son impuestas usando una capa de celdas ficticias alrededor de la
malla o red. La figura 4.2.2.1 esquematiza la aplicación de las condiciones de bordes para el límite
izquierdo. Cuando las condiciones de bordes son de tipo Dirichlet, se tiene (Lemos, 1997):
ϕ ij = 2ϕ b − ϕ 2 j
donde
(7)
ϕ = v, T , que es cuando la variable en cuestión es definida en los bordes, este valor de equilibrio
es impuesto directamente. Para variables que no son definidas en una locación exacta de los bordes, los
valores de “afuera” son obtenidos por interpolación. Tales valores son entonces usados para evaluar
∂ ( ) / ∂z y ∂ 2 ( ) / ∂z 2 en los bordes, usando la misma expresión como en los puntos anteriores, esto es
llamado técnica de reflexión. Los métodos de extrapolación conducen a una pérdida de la exactitud
cerca de los bordes (Taylor y Peyret, 1983). Una mayor exactitud en las condicione de bordes pueden ser
implementadas, pero estas requieren un tratamiento separado para las derivadas ∂ (
(Lemos, 1997).
) / ∂z
y ∂
2
( ) / ∂z 2 ,
125
j+1
ϕ
U
V
j
ϕ
i=1
ϕ
U
i=2
Figura 4.2.2.1: Esquematización de las condiciones de bordes para el borde izquierdo.
Modificado de Lemos, 1997
Cuando las condiciones de bordes tipo Neumann son aplicadas, se tiene:
ϕ1 j = ϕ 2 j − ∆z (∂ϕ / ∂z )b = ϕ 2 j − ∆z (q / υvϕ )b
donde
(8)
q = τ si ϕ = v . De nuevo, mayor exactitud puede ser formulada considerando un solo lado en las
aproximaciones de alto orden para las derivadas, involucrando más valores de
ϕ
en la malla.
Condiciones de bordes tipo mixtas (Robin) pueden ser impuestas de la misma manera (Lemos, 1997).
Consideraciones de estabilidad
El propósito del análisis de estabilidad es determinar las condiciones por las cuales, sobre
repetidas aplicaciones del esquema numérico en las condiciones iniciales, el error parece limitado una
vez que el tamaño del paso en tiempo (delta t) y el espaciamiento de la malla (delta x) han sido definidos.
En cálculos de fluidos incomprensibles, inestabilidades pueden ser generadas en la ecuación de
momentum discretizada. Los grandes problemas concerniente a la estabilidad son expuestos por la
aproximaciones explicitas para la ecuación momentum. Debido a que esta ecuación no es lineal, un
análisis completo
no es posible. Sin embargo, condiciones aproximadas de estabilidad pueden ser
126
obtenidas “congelando la no- linealidad”. Un análisis Fourier-von Neumann de esquemas FTCS en 2D da
los siguientes contrastes para el diferencial de tiempo máximo permisible (Lemos, 1997):
∆t ≤
∆x 2 ∆y 2
2υ ∆x 2 + ∆y 2
∆t ≤
2υ
max u 2 + υ 2
(
∆t ≤ min
{
∆x ∆y
,
u υ
)
(9)
}
(10)
(11)
Condición (9) es más restrictiva para fluidos altamente viscosos, mientras que la condición (10)
es limitante para flujo dominado por convección. Finalmente, la tercera inecuación es la condición (11)
Courant-Friedrichs-Levy (CFL), la cual establece que el material no se puede mover mas de una celda en
un diferencial de tiempo (Lemos, 1997).
Inestabilidades no lineales pueden desarrollar en términos largos integraciones de flujos de altoRe o flujos geofísicos con pequeñas disipación, cuando el fenómeno de aliasing asociado con longitudes
de ondas mas cortas que dos veces el espaciamiento de la red puede conducir a una contaminación
significante de la solución de longitudes de ondas largas (e.g. Haltiner y Williams, 1980).
ALGORITMO DE DIFERENCIA FINITA
Las ecuaciones (1),(2) y (3) presentadas en el capitulo 4 fueron discretizadas usando un arreglo
alternativo o escalonado del grid implementado anteriormente por Carlos Lemos en 1994, autor de este
algoritmo. Una capa de celdas ficticias alrededor de la malla es usada para facilitar la imposición de las
127
condiciones de bordes. La figura 6.2.1 ilustra la localización de las variables dependientes en una celda
típica de la malla, así como el control del volumen considerado por la discretización conservativa de las
variable escalar T y dado el caso las componentes de la velocidad. Este control de volúmenes son
cambiados en el espacio, debido a la estructura de la malla (Lemos, 1997).
El algoritmo modificado en este trabajo consiste en los siguientes pasos:
0)
Fija v =constante y T=T0
1) Calcula la temperatura a un tiempo dado Tn+1 , usando una aproximación de diferencia finita
para la ecuación (3), ver capitulo 4.
2) Copia los arreglos avanzados de tiempo en un arreglo de tiempo n.
3) Prueba si el tiempo final a sido alcanzado; si es cierto para los cálculos, de otra manera
retorna al paso 1.
Tomando
ejemplo:
ϕ
como una variable dependiente para la cual hay una ecuación de transporte, por
ϕ = T , los valores de ϕ
para un tiempo dado son obtenidos usando el explicito esquema de
Euler, presentado a continuación:
ϕijn+1 = ϕijn + ∆t −
1
+
∆x
en el cual
v ∆ϕ
σ ϕ ∆x
i +1 / 2 j
[
]
[
1
(uϕ )i+1/ 2 j − (uϕ )i−1/ 2 j − 1 (uϕ )ij+1/ 2 − (uϕ )ij−1/ 2
∆t
∆y
v ∆ϕ
−
σ ϕ ∆x
i +1 / 2 j
1
+
∆y
v ∆ϕ
σ ϕ ∆y
ij +1 / 2
v ∆ϕ
−
σ ϕ ∆y
]
n
+ Sϕ
(*)
ij −1 / 2
S ϕ es un término origen. Para u y v . S ϕ incluye el termino de equilibrio y el termino del
gradiente de presión es evaluado en tiempo n. Para completar la formulación en el esquema diferencial,
los flujos convectivos y difusivos en lasa caras de las celdas
volumen
ϕ
debe ser evaluado en términos de los valores de
ϕ
i+1/2j, i-1/2j, ij-1/2 y ij+1/2
del control de
en los nodos del grid (Lemos, 1997).
128
La ecuación (*) es la ecuación programada en el código original, la cual fue reducida a términos
más simples en el programa modificado para ser implementado en este trabajo, ya que se opto trabajar
en una sola dimensión (1D), (Lemos, 1997).
Los flujos difusivos (por ejemplo: (v / σ ϕ ) ∆ϕ / ∆x ) son calculados usando la aproximación
centrada-diferencia empleada en previos códigos FDFLOW, donde las difusividades son obtenidas por
interpolación cuando es necesario. Aunque las aproximaciones para los diferentes flujos son
relativamente directas, las interpolaciones para
ϕ
en los flujos advectivos requieren cuidadosas
consideraciones. Las alternativas más simples son el uso de la interpolación lineal:
(uϕ )i +1 / 2 j
= u i +1 / 2 j
1
(ϕ i+1 j + ϕ ij )
2
(**)
o el método de “upwind”
(uϕ )i +1 / 2 j = ϕ ij max(ui +1 / 2 j ,0) − ϕ i +1 j max(− ui +1 / 2 j ,0)
(***)
Las ecuaciones (**) y (***) conducen a la implementación del esquema FTCS (Forward –TimeCentered Space) y también del esquema “upwind” de primer orden. El esquema FTCS introduce falsas
oscilaciones en la solución numérica, mientras que el esquema “upwind” es excesivamente difusivo. Para
superar los defectos de los esquemas FTCS y “upwind” , manteniendo las ventajeas de ambos, varias
alternativas han sido propuestas, tal como la extrapolación “upwind” (por ejemplo: Thakur and Shyy,1993)
(uϕ )i +1 / 2 j
=
1
(3ϕ ij − ϕ i−1 j )max(ui+1 / 2 j ,0) − 1 (3ϕ i +1 j − ϕ i+2 j )max(− ui +1 / 2 ,0)
2
2
(****)
129
DESCRIPCION DEL ALGORITMO COMPUTACIONAL FDTHERM_1D
El programa computacional FDTHERM_1D
fue escrito en dos archivos separados,
FDTHERM_1D.INC y FDTHERM_1D.FOR es un archivo incluido el cual contiene las definiciones para las
constantes (parámetros) y variables globales usadas por todas las unidades del programa, junto con una
corta descripción de cada variable. Este glosario de símbolos de FORTRAN puede ser usado para la
lectura y modificación del código original, o para preparar la data de entrada para un nuevo problema. El
archivo FDTHERM_1D.FOR contiene el programa principal (MAIN) y el conjunto de subrutinas que el
algoritmo implementa. El programa fue escrito en forma de subrutinas, cada unidad del programa ejecuta
una singular tarea. A continuación se da una breve descripción de las unidades o subrutinas del
programa usadas en FDTHERM_1D:
MAIN comienza con una sección de inicialización, y proporciona un control cíclico sobre los
cálculos. MAIN llama a las subrutinas CALCT Y FPRINT.
BC fija todas las condiciones de bordes para las variables de campo, sobrescribiendo los valores
guardados en capas de celdas ficticias alrededor de la malla o red. Las condiciones de bordes por
defecto, según el código actual modificado son : (i) Condiciones de bordes tipo Dirichlet en los límites
verticales de la malla y (ii)condiciones de bordes tipo Neumann en los bordes horizontales para T. Las
variables de campo y sus derivadas son especificadas usando los arreglos TB y DTDNB, una descripción
detallada puede ser encontrada en el glosario de variables contenido en el archivo FDTHERM_1D.INC.
Condiciones de bordes especiales pueden ser insertadas en el programa, usando las localizaciones
marcadas para ese propósito. BC es llamado por CALCT y SETUP.
CALCT calcula la temperatura a un tiempo avanzado Tn+1 apartir de una velocidad constante v.
Los flujos advectivos pueden ser calculados usando una interpolación lineal, “upwind” o métodos TVD
130
(Total Variation Diminishing). El método para aproximar el término advectivo es seleccionado usando la
variable golbal METHOD. CALCT es llamado por MAIN y llama a BC.
FPRINT imprime un mensaje en el terminal con el tiempo de corrida del programa y escribe los
valores de las variables de control y de campo en un archivo FLOWnnn.OUT cuando el tiempo para la
próxima salida es alcanzado, nnn es calculado internamente por la variable entera FCOUNT. FPRINT es
llamado por MAIN y por BC.
SETUP lee los archivos de entrada y el de las condiciones de bordes, fd.txt, fdtherm.txt y bc.txt,
e inicializa el control y las variables de campo. El archivo fd.txt contiene tres columnas, KT, H y T,
representa un modelo inicial. El archivo fdtherm.dat contiene los parámetros de entrada que definen la
malla, el ciclo de control de las variables y los parámetros. El archivo bc.dat contiene las variables por
defecto para las variables dependientes y sus derivadas. SETUP es llamado por MAIN.
El código original puede ser usado para simular muchos fenómenos de flujos con cambios
relativamente pequeños. Típicamente estos cambios son confinados en las subrutinas BC y SETUP. En
este trabajo se modifico el código original para obtener resultados en una sola dimensión (1D) y calcular
la variación de la temperatura con el tiempo, a partir de una velocidad de fluido constante.
CODIGO fdtherm_1d
====================== PROGRAM "FDTHERD_1D.FOR" : =======================C
C A Simple program for computing incompressible fluid flows
C
C with buoyancy effects, using the Boussinesq approximation
C
C
C
C
Carlos M. Lemos, May 1994
C
C=========================================================================C
PROGRAM MAIN
INCLUDE 'fdtherm_1d.inc'
C
C
** INITIALIZE VARIABLES AND PRINT INITIAL DATA
CALL SETUP
131
CALL PRINTF
C ** START MAIN CYCLE
C
10 CONTINUE
C
C
C
C
C
C
C
C
C
C
C
C
** COMPUTE ADVANCED-TIME SCALAR VARIABLES
CALL CALCT1D
** COPY THE ADVANCE TIME ARRAYS TO TIME-N ARRAYS
DO I=1,IMAX
TN(I)=T(I)
ENDDO
** ADVANCE TIME AND CYCLE COUNTER
TIME=TIME+DELT
CYCLES=CYCLES+1
** PRINT CYCLE INFORMATION & FIELD VARIABLES
CALL PRINTF
IF (TIME.GT.TWFIN) STOP 'End of Program'
GOTO 10
END
SUBROUTINE BC
INCLUDE 'fdtherm_1d.inc'
C
C
C
** SET BOUNDARY CONDITIONS
** IVAR IS = 1 FOR TEMPERATURE
C
** SPECIAL BOUNDARY CONDITIOS FOR T
IF (IMETHOD==1) THEN
T(1)=2.*TB(1)-T(2)
T(IMAX)=2.*TB(2)-T(IM1)
ELSE IF (IMETHOD==2) THEN
T(1)=T(2)-DTDNB(1)*DELZ
T(IMAX)=T(IM1)+DTDNB(2)*DELZ
ELSEIF (IMETHOD==3) THEN
T(1)=2.*TB(1)-T(2)
T(IMAX)=T(IMAX-1)+DTDNB(2)*DELZ
ENDIF
RETURN
END
C
C
C
SUBROUTINE CALCT1D
INCLUDE 'fdtherm_1d.inc'
** COMPUTE ADVANCED-TIME TEMPERATURE
SMALL=1.E-30
DO I=1,IM1
VFACE=VZ(I)
132
CTERMAL=0.5*(KT(I)+KT(I+1))
TADVECTION=RHO(I)*CV(I)*TN(I)+RHO(I+1)*CV(I+1)*TN(I+1)
CFLUX=VFACE*TADVECTION*0.5
&
-CTERMAL*RDZ*(TN(I+1)-TN(I))
CFL=VZ(I)*DTDZ
IP=MIN(I+1,IM1)
IM=MAX(I-1,1)
CFLP=VZ(IP)*DTDZ
CFLM=VZ(IM)*DTDZ
!
DPHI=TN(I+1)-TN(I)
DPHIP=TN(IP+1)-TN(IP)
DPHIM=TN(IM+1)-TN(IM)
GPHI=0.5*(ABS(CFL)-CFL**2)*DPHI
GPHIP=0.5*(ABS(CFLP)-CFLP**2)*DPHIP
GPHIM=0.5*(ABS(CFLM)-CFLM**2)*DPHIM
SIG=SIGN(1.0,GPHI)
IF (GPHI.LT.0.0) THEN
SIG=-1.0
ELSE
SIG=1.0
ENDIF
G1=SIG*AMAX1(0.0,AMIN1(ABS(GPHI),SIG*GPHIM))
G2=SIG*AMAX1(0.0,AMIN1(ABS(GPHI),SIG*GPHIP))
GGAM=SIG*(G2-G1)/(ABS(DPHI)+SMALL)
ADIFF=0.5*(G2+G1)/DTDZ
DIFF=-0.5*ABS(CFL+GGAM)*DPHI/DTDZ
FLUXX(I)=CFLUX+IUPWND*DIFF+IFCTS*ADIFF
ENDDO
DO I=2,IM1
PROV_TERM = -DELT*RDZ*(FLUXX(I)-FLUXX(I-1))
PROV_TERM=PROV_TERM/(RHO(I)*CV(I))
T(I)=TN(I)+ PROV_TERM
T(I)=T(I)+ DELT*((N_R*H(I)*RHO(I))/(RHO(I)+CV(I)))
ENDDO
CALL BC
RETURN
END
SUBROUTINE PRINTF
INCLUDE 'fdtherm_1d.inc'
C
C
C
C
CHARACTER*11 FILENAME
** PRINT CYCLE INFORMATION AND FIELD VARIABLES
WRITE(*,50)ITER,TIME,CYCLES
IF (CYCLES.LE.0.OR.TIME+1E-06.GE.TWPRT) THEN
FILENAME=' '
FILENAME(1:4)='FLOW'
WRITE(FILENAME(5:7),46)FCOUNT+100
FILENAME(8:11)='.OUT'
OPEN(6,FILE=FILENAME,STATUS='UNKNOWN')
WRITE(6,40)ITER
WRITE(6,41)TIME
WRITE(6,42)CYCLES
133
WRITE(6,47)
DO I=1,IMAX
WRITE(6,48)KT(I),H(I),T(I)
ENDDO
CLOSE(6)
TWPRT=TWPRT+PRTDT
FCOUNT=FCOUNT+1
ENDIF
RETURN
40 FORMAT(I8,' ITER')
41 FORMAT(F8.3,' TIME')
42 FORMAT(I8,' CYCLE')
46 FORMAT(I3)
47 FORMAT(3X,'KT',3X,'H',11X,'T')
48 FORMAT(2X,F5.2,1X,F6.2,1X, F7.3)
C50 FORMAT(10X,'ITER=',I5,10X,'TIME=',1PE12.5,10X,'CYCLE=',I6)
END
SUBROUTINE SETUP
INCLUDE 'fdtherm_1d.inc'
DOUBLE PRECISION K_MAX,K_0,MA
C
C
C
** READ INPUT PARAMETERS
WRITE(*,*)'INTRODUZCA PROFUNDIDAD DE MODELADO (m)'
READ(*,*)L
WRITE(*,*)'INTRODUZCA TEMPERATURA DE REFERENCIA (oC)'
READ(*,*)T_0
WRITE(*,*)'INTRODUZCA DENSIDAD DE REFERENCIA (Kg/m3)'
READ(*,*)RHO_0
WRITE(*,*)'INTRODUZCA CALOR ESPECIFICO DE REFERENCIA (J/KgxoC)'
READ(*,*)CV_0
WRITE(*,*)'INTRODUZCA PRODUCCION DE CALOR DE REFERENCIA (W/Kg)'
READ(*,*)H_0
IF (H_0.GT.0.0) THEN
WRITE(*,*)'INTRODUZCA QM, FLUJO DE CALOR MANTELAR (mW/m2)'
READ(*,*)QM
QM=QM*1.0E-3
ENDIF
WRITE(*,*)'INTRODUZCA CONDUCTIVIDAD TERMAL DE REF. (J/m*oC)'
READ(*,*)K_0
N_R= (H_0*RHO_0*L*L)/(K_0*T_0)
WRITE(*,*)'INTRODUZCA NUMERO DE NODOS'
READ(*,*)INODOS
IMAX=INODOS+2
DELZ=L/REAL(INODOS)
T_MAX=T_0
K_MAX=K_0
RHO_MIN=RHO_0
H_MIN=H_0
CV_MIN=CV_0
V_0=(K_0/(L*RHO_0*CV_0))
V_MAX=V_0
OPEN(4,FILE='fd.txt',STATUS='OLD')
DO I=2,IMAX-1
READ(4,*)KT(I),H(I),VZ(I),RHO(I),CV(I),T(I)
T_MAX=MAX(T_MAX,T(I))
K_MAX=MAX(K_MAX,KT(I))
RHO_MIN=MIN(RHO_MIN,RHO(I))
134
IF (H(I).GT.0.0) H_MIN=MIN(H_MIN,H(I))
CV_MIN=MIN(CV_MIN,CV(I))
V_MAX=MAX(V_MAX,VZ(I))
KT(I)=KT(I)/K_0
IF (H_0.NE.0.) H(I)=H(I)/H_0
IF (V_0.NE.0.) VZ(I)=VZ(I)/V_0
RHO(I)=RHO(I)/RHO_0
CV(I)=CV(I)/CV_0
T(I)=T(I)/T_0
ENDDO
CLOSE(4)
! CALCULAR DELT
DELT1=0.5*(DELZ*DELZ*RHO_MIN*CV_MIN)/K_MAX
IF (V_MAX.GT.0.0) THEN
DELT2=0.5*DELZ/V_MAX
ELSE
DELT2= DELT1
ENDIF
DELT3=DELZ*DELZ*0.5*((H_MIN*RHO_MIN)/(K_MAX*T_MAX))
IF (DELT3.LE.0.0) DELT3=DELT1
DELT=MIN(DELT1,DELT2,DELT3)*1.0D-2
WRITE(*,*)'VALOR DE DELT EN UNIDADES DE m.a'
MA=3.1536E14
DELT_MA=DELT/MA
WRITE(*,*)DELT_MA,N_R
WRITE(*,*)'NUEVO VALOR DE DELT EN m.a'
READ(*,*)DELT_MA
DELT=DELT_MA*MA
WRITE(*,*)'INTRODUZCA TWFIN (m.a)'
READ(*,*)TWFIN
WRITE(*,*)'INTRODUZCA PRTDT (m.a)'
READ(*,*)PRTDT
WRITE(*,*)'INTRODUZCA METHOD'
READ(*,*)METHOD
TWFIN=TWFIN*MA
PRTDT=PRTDT*MA
C
C
C
** READ BOUNDARY CONDITIONS
OPEN(5,FILE='bc.txt',STATUS='OLD')
READ(5,*)IMETHOD
READ(5,*)TB(1),TB(2)
READ(5,*)DTDNB(1),DTDNB(2)
CLOSE(5)
C
C
** INITIALIZE AUXILIARY AND CONTROL VARIABLES
IM1=IMAX-1
DELZ=DELZ/L
QM=QM*L/(K_0*T_0)
DELT=((DELT*K_0)/(L*L*RHO_0*CV_0))
TWFIN=((TWFIN*K_0)/(L*L*RHO_0*CV_0))
PRTDT=((PRTDT*K_0)/(L*L*RHO_0*CV_0))
RDZ=1.0/DELZ
TB(1)=TB(1)/T_0
TB(2)=TB(2)/T_0
DTDNB(1)=DTDNB(1)*(L/T_0)
DTDNB(2)=DTDNB(2)*(L/T_0)
TIME=0.0
ITER=0
135
CYCLES=0
TWPRT=0.0
FCOUNT=0
DTDZ=DELT*RDZ
C
C
C
C
C
C
IF (METHOD.EQ.1) THEN
IUPWND=0
IFCTS=0
ELSEIF (METHOD.EQ.2) THEN
IUPWND=1
IFCTS=0
ELSE
IUPWND=1
IFCTS=1
ENDIF
** SET INITIAL FIELDS
CALL BC
** INITIALIZE TIME-N ARRAYS
DO 40 I=1,IMAX
TN(I)=T(I)
40 CONTINUE
KT(1)=0.0
KT(IMAX)=KT(IMAX-1)
RHO(1)=0.0
RHO(IMAX)=RHO(IMAX-1)
CV(1)=0.0
CV(IMAX)=CV(IMAX-1)
VZ(1)=0.0
IF (IMETHOD.EQ.3) THEN
DTDNB(2)=QM*2.0/(KT(IMAX)+KT(IMAX-1))
ENDIF
RETURN
END
C=====================================
136
RETRO-EVOLUCIÓN O BACKSTRIPPING
Este algoritmo computacional compilado en Fortran 77, para el calculo de la subsidencia total e
isotática en una sola dimensión (Isostacia tipo Airy), el código original fue desarrollado por Allen y Allen
(1990).
DESCRIPCIÓN DEL ALGORITMO
El archivo backstripping.f contiene una programa principal y cuatro subroutinas que el algoritmo
utiliza, cada una de ellas calcula una tarea en particular. A continuación se da una breve descripción de
cada una de las partes y/o subroutinas del programa:
El programa principal: primero el programa pide al usuario que introduzca el numero de
unidades o capas que van a descompactarse (número de filas que contiene el archivo de entrada), luego
lee el archivo de entrada, el cual puede tener cualquier nombre (es introducido por el usuario), este
archivo debe contener el número de unidades, L(i), tope de la unidad, Zt(i), base de la unidad, Zb(i),
coeficiente de porosidad-profundidad, C(i) y la porosidad inicial, suport(i) características de esa unidad,
ver tabla 1. El programa principal llama a las subroutinas Solution, Porosidad, Densidad y Isostacia.
Solution: calcula las profundidades después de la descompactación (subsidencia total), a través
de un método numérico iterativo, es decir, en el programa se establece una condición que debe cumplirse
para que pueda realizar el siguiente paso. Ver capitulo 3, ec. 8.
Porosidad: calcula la porosidad después de la descompactación, a través de una relación
exponencial dependiente de la profundidad, (ver capitulo 3, ec. 1), y utilizando las profundidades
descompactadas halladas en la subroutina anterior.
137
Densidad: calcula la densidad de las unidades descompactadas, a partir de los espesores y
porosidades de las nuevas unidades descompactadas ver capitulo 3 (ecuaciones 10 y 11).
Isostasia: calcula la subsidencia isostática, a partir de los nuevos espesores descompactados,
también toma en cuanta el efecto de las nuevas densidades, la paleobatimetría y los cambios eustáticos
del nivel del mar. Ver capitulo 3, ec. 13.
ARCHIVOS DE ENTRADA
Unidad
Tope (km)
Base (km.)
c (1/km.)
φo
gr/cc
Wd (km)
∆sl (km)
1
2.171
2.467
0.27
0.49
2650
0.1
0.163
2
1.577
2.171
0.51
0.63
2250
0.2
0.12
3
0
1.577
0.51
0.63
2250
0
0.136
Tabla 1: Data de entrada correspondiente a la región de Guarico Norte, antes de la descompactación.
Unidad
Tope (km)
Base (km.)
c (1/km.)
φo
gr/cc
Wd km)
∆sl (km)
1
4.826
5.226
0.27
0.49
2650
0.1
0.163
2
4.187
4.826
0.51
0.63
2250
0
0.04
3
2.331
4.187
0.51
0.63
2250
0
0.136
4
1.271
2.331
0.51
0.63
2250
0.007
0.043
5
0
1.271
0.27
0.49
2250
0
0.02
Tabla 2: Data de entrada correspondiente a la región de Maturín Oeste, antes de la descompactación.
Unidad
Tope (km.)
Base (km.)
c (1/km)
Φo
gr/cc
Wd (km)
∆sl (km)
1
6.480
6.680
0.27
049
2650
0.05
0.0815
2
5.081
6.480
0.27
0.49
2650
0.1
0.163
3
4.668
5.081
0.27
0.49
2250
0.1
0.12
4
4.116
4.668
0.51
0.63
2250
0
0.045
5
2.820
4.116
0.51
0.63
2250
0.2
0.147
6
0
2.820
0.51
0.63
2250
0.1
-0.047
Tabla 3: Data de entrada correspondiente a la región de Maturín Norte, antes de la descompactación.
138
Unidad
Tope (km.)
Base (km.)
c (1/km)
Φo
gr/cc
Wd (km)
∆sl (km)
1
5.670
5.870
0.27
0.49
2650
0.05
0.14
2
5.214
5.670
0.27
0.49
2650
0.1
0.163
3
4.855
5.214
0.27
0.49
2250
0.1
0.095
4
2.776
4.855
0.51
0.63
2250
0
0.14
5
0
2.776
0.27
0.49
2250
0
-0.047
Tabla 4: Data de entrada correspondiente a la región de Maturín Centro, antes de la descompactación.
CÓDIGO DEL ALGORITMO DE BACKSTRIPPING
program backstrpping
character(len=12) :: fname0
common N, i, j,Ratio,x
double precision A,B,Lhs,R
double precision D
common Zt, Zb, T, C, surpor,Ma
double precision Nzb,Nzt,Por,Dt
double precision rhoa,rhos,Tect,W,SL,K
C W = paleowater depth, sl=nivel del mar relativo al presente
dimension L(200)
dimension Zt(200),Zb(200),T(200),C(200),surpor(200),Ma(201)
dimension Nzt(200,200), Nzb(200,200),Por(200,200),Dt(200,200)
dimension rhoa(200),rhos(200),Tect(200),W(200),SL(200),K(200)
write(*,*)'numero de unidades estratigráficas'
read(*,*)N
write(*,*) 'nombre del archivo de datos (.txt)'
read(*,*) fname0
c Lectura del archivo de entrada, Introduzca el filename.txt
open(1,FILE=fname0)
do i=1,N
read(1,*) L(i),Zt(i),Zb(i),C(i),surpor(i),rhos(i),W(i),SL(i)
T(i)=Zb(i)-Zt(i)
end do
close(1, status = 'KEEP')
write(*,*)'Data estratigrafica'
write(*,*)'unidad tope base coef surpor '
do i=1,N
write(*,'(I7,3f9.3,2f7.2)') L(i),Zt(i),Zb(i),C(i),surpor(i)
enddo
pause
do j=1,N
do i=j,N
x=i-j+1
Ratio=surpor(x)/C(x)
write(*,*)'Ratio vale:'
write(*,*) Ratio
if (j.eq.1) then
139
Nzt(i,j)=0
else
Nzt(i,j)=Nzb(i,j-1)
write(*,*) 'Nzt(i,j) = Nzb(i,j-1)'
write(*,*) Nzt(i,j),Nzb(i,j-1)
endif
call Solution(Nzb,Nzt)
enddo
enddo
write(*,*) Nzb(i,j)
write(*,*)'i j Profundidades descompactadas'
do j=1,N
do i=1,N
write(*,*) i,j,Nzb(i,j)
enddo
write(*,*)
enddo
do i=1,N+1
if (i.eq.1) then
write(*,*)'edad de inicio de la subsidencia'
read(*,*)Ma(1)
else
write(*,*)'edad del tope de la unidad',L(i-1)
read(*,*)Ma(i)
endif
enddo
write(*,*)
write(*,*) 'Espesores descompactados'
write(*,*)
do i=1,N
do j=1,i
Dt(i,j)=Nzb(i,j)-Nzb(i,j-1)
enddo
enddo
do j=1,N
do i=1,N
write(*,*)Dt(i,j)
enddo
enddo
call porosidad(D,Por,Nzb,Dt)
call densidad(rhoa,rhos,Por,Nzb,Dt)
write(*,*)
call isostacia(Tect,rhoa,Nzb,W,SL,K)
c Archivo de Salida: Profundidades descompactadas
open(3,file='c:Nzb.txt',status='unknown')
do j=1,N
do i=1,N
write(3,200) L(i),Ma(i+1),Nzb(i,j)
200
format(I5,I5,3f9.3)
enddo
enddo
c Archivo de Salida: Porosidad-Densidad
open(4,file='c:por-rhoa.txt',status='unknown')
140
do j=1,N
do i=1,N
write(4,300) L(i),Ma(i+1),Por(i,j),rhoa(i)
300
format(I5,I5,3f9.3,3f9.3)
enddo
enddo
c Archivo de Salida: Subsidencia Tectonica
open(5,file='c:tect.txt',status='unknown')
do i=1,N
write(5,400) Ma(i+1),Tect(i)
400
format(I5,3f9.3)
enddo
end
subroutine Solution(Nzb,Nzt)
COMMON N,i,j,Ratio,x
double precision A,B,Lhs,R
COMMON Zt,Zb,T,C,surpor
double precision Nzb,Nzt
dimension Zt(200),Zb(200),T(200),C(200),surpor(200)
dimension Nzt(200,200),Nzb(200,200)
write(*,*)'C(x),Zt(x),Zb(x)'
write(*,*) C(x),Zt(x),Zb(x)
A=EXP(-C(x)*Zt(x))-EXP(-C(x)*Zb(x))
write(*,*)'A vale:'
write(*,*) A
write(*,*)'C(x),Nzt(i,j)'
write(*,*) C(x),Nzt(i,j)
B=exp(-C(x)*Nzt(i,j))
write(*,*)'B vale:'
write(*,*) B
write(*,*)'Nzt(i,j),i,j,T(x),Ratio,A,B'
write(*,*) Nzt(i,j),i,j,T(x),Ratio,A,B
Lhs=Nzt(i,j)+T(x)-(Ratio*A)+(Ratio*B)
write(*,*)'Lhs vale:'
write(*,*) Lhs
Nzb(i,j)=1
do while ((R<0.9999*Lhs).or.(R>1.0001*Lhs))
write(*,*)'Nzb(i,j),Ratio,C(x)'
write(*,*) Nzb(i,j),Ratio,C(x)
R=Nzb(i,j)+Ratio*exp(-C(x)*Nzb(i,j))
write(*,*)'R vale:'
write(*,*) R
if (R>1.0001*Lhs) then
write(*,*)'Nzb(i,j),Lhs,R'
write(*,*) Nzb(i,j),Lhs,R
Nzb(i,j)=Nzb(i,j)-ABS(Lhs-R)
end if
if (R<0.9999*Lhs) then
write(*,*)'Nzb(i,j),Lhs,R'
write(*,*) Nzb(i,j),Lhs,R
Nzb(i,j)=Nzb(i,j)+ABS(Lhs-R)
end if
enddo
141
end
subroutine porosidad(D,Por,Nzb,Dt)
COMMON N,i,j,Ratio,x
double precision D
COMMON Zt,Zb,T,C,surpor
double precision Nzb,Nzt,Por,Dt
dimension Zt(200),Zb(200),T(200),C(200),surpor(200)
dimension Nzb(200,200),Nzt(200,200),Por(200,200),Dt(200,200)
do i=1,N
do j=1,i
x=i-j+1
write(*,*)'surpor
C(x)'
write(*,*)surpor(x),C(x)
Ratio=surpor(x)/C(x)
write(*,*)'Ratio vale:'
write(*,*)Ratio
write(*,*)'C(x)'
write(*,*)C(x)
write(*,*)'Nzb(i,j-1)'
write(*,*)Nzb(i,j-1)
write(*,*)'Nzb(i,j) vale:'
write(*,*)Nzb(i,j)
D=exp(-C(x)*Nzb(i,j-1))-exp(-C(x)*Nzb(i,j))
write(*,*)'D vale:'
write(*,*) D
c
Por=Porosidad de la capa despues de la descompactacion
write(*,*)'Ratio
D
write(*,*) Ratio,D,Dt(i,j)
Dt
valen:'
Por(i,j)=(Ratio*D)/Dt(i,j)
write(*,*)'Por vale:'
write(*,*) Por(i,j)
enddo
enddo
end
subroutine densidad(rhoa,rhos,Por,Nzb,Dt)
COMMON N,i,j
double precision Nzb,Nzt,Por,Dt
double precision rhoa,rhos
dimension Nzb(200,200),Nzt(200,200),Por(200,200),Dt(200,200)
dimension rhoa(200),rhos(200)
rhow=1030
write(*,*)'rhow'
write(*,*)rhow
do i=1,N
rhoa(i)=0
do j=1,i
c rhoa= la nueva densidad de bulk de la columna sedimentaria completa
write(*,*)'rhoa(i) Por(i,j) rhos(i) Nzb(i,i) Dt(i,j)'
write(*,*) rhoa(i),Por(i,j),rhos(i),Nzb(i,i),Dt(i,j)
rhoa(i)=rhoa(i)+((Por(i,j)*rhow)+((1-Por(i,j))*rhos(i)))
1*Dt(i,j)/Nzb(i,i)
142
write(*,*)'rhoa vale:'
write(*,*)rhoa(i)
enddo
enddo
end
subroutine isostacia(Tect,rhoa,Nzb,W,SL,K)
common N,i,j
double precision Nzb
double precision rhoa,rhos,Tect,W,SL,K
dimension rhoa(200),rhos(200),Tect(200),W(200),sl(200),k(200)
dimension Nzb(200,200)
rhom=3300
rhow=1030
do i=1,N
write(*,*)'Nzb(i,i) rhom rhoa(i) rhow valen:'
write(*,*)Nzb(i,i),rhom,rhoa(i),rhow
m=0.4537
k(i)=W(i)-SL(i)
Tect(i)=Nzb(i,i)*(rhom-rhoa(i))/(rhom-rhow)-SL(i)*m+K(i)
c Tect= es la profundidad del basamento corregida por carga sedimentaria
write(*,*)'Tect vale:'
write(*,*) Tect(i)
enddo
end