da click aquí - Ecuacion Diferencial Ejercicios Resueltos
Anuncio
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
MÉTODO DE EULER PARA ECUACIONES
DIFERENCIALES
Al culminar de leer el siguiente artículo, podrás resolver cualquier ecuación diferencial de primer orden con
valores iniciales, mediante el método de euler para ecuaciones diferenciales y además podrás gracar tus
resultados aquí mismo o copiando el código de MATHEMATICA al nal del artículo.
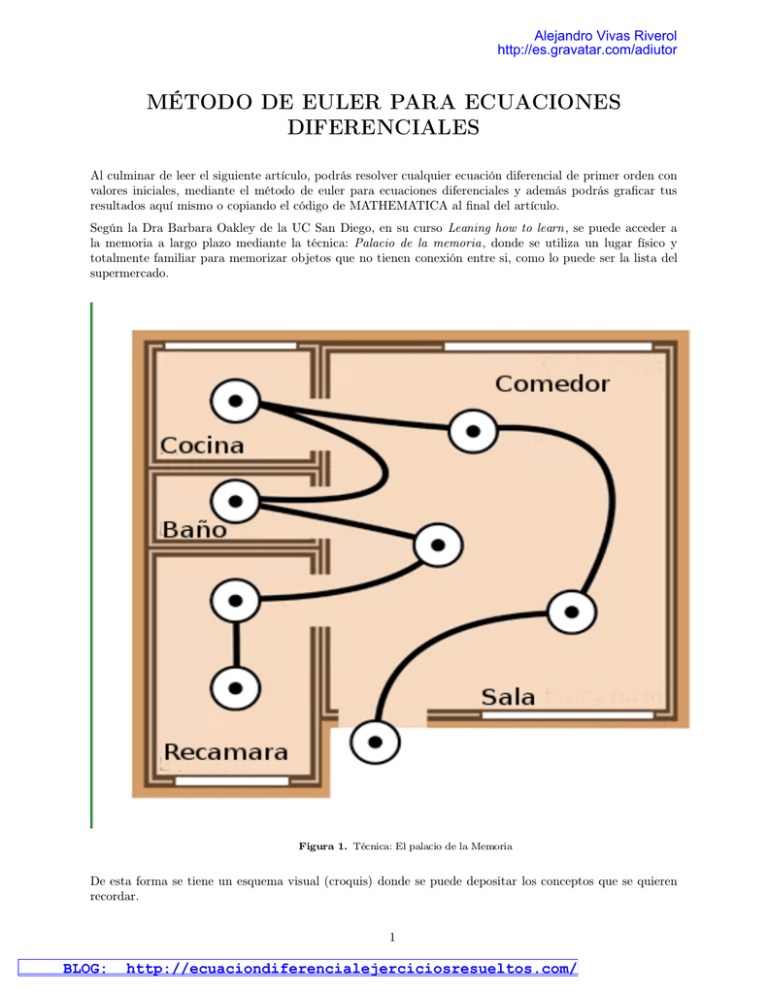
Según la Dra Barbara Oakley de la UC San Diego, en su curso Leaning how to learn, se puede acceder a
la memoria a largo plazo mediante la técnica: Palacio de la memoria, donde se utiliza un lugar físico y
totalmente familiar para memorizar objetos que no tienen conexión entre si, como lo puede ser la lista del
supermercado.
Figura 1. Técnica: El palacio de la Memoria
De esta forma se tiene un esquema visual (croquis) donde se puede depositar los conceptos que se quieren
recordar.
1
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
Así el ubicar los objetos de la lista en cada uno de los resintos de nuestro lugar físico familar y dar un
paseo, nos ayudará a recordar dicha lista; también es importante que los objetos depositados en el recinto
tengan alguna exageración, como lo puede ser en su tamaño o forma.
Esta es otra técnica que se podría emplear para memorizar los pasos que aquí proponemos para resolver los
tipos de ecuaciones diferenciales.
METODO DE 4 PASOS PARA RESOLVER ECUACIONES
DIFERENCIALES DE PRIMER ORDEN CON VALORES
INICIALES MEDIANTE EL MÉTODO DE EULER
FORMULAS USADAS
yn+1 = yn + hf (xn ; yn)
(1)
xn+1 = xn + h
(2)
Donde:
n = 0; 1; 2; 3; :::
h = tamaño del incremento en x
f (xn ; yn) = segundo mienbro de la ED de primer orden cuando tiene la forma:
dy
dx
= f(x; y)
PROCEDIMIENTO:
i. Escribimos la ED en la forma:
dy
dx
= f (x; y), para extrar su segundo miembro
ii. Denimos x0, y0 y h de acuerdo a los datos del problema, ejemplo:
p
para el PVI: y 0 = 0.12 y + 0.4x2, y(2) = 4, y(2.5), con h = 0.5, las variables buscadas son: x0 = 2,
y0 = 4 y h = 0.5
iii. Plateamos la ecuación de Euler utilizando los datos iniciales, como sigue:
y0+1 = y0 + hf (x0; y0)
Y una vez obtenido este primer resultado repitimnos el proceso iterativamente utilizando los nuevos
datos:
y1+ 1 = y1 + hf (x1; y1)
iv. Desarrollamos hasta el valor buscado en x, en este caso: x = 2.5, como se ve el los datos del problema
del inciso ii.
EJEMPLOS RESUELTOS DE ECUACIONES DIFERENCIALES
DE PRIMER ORDEN CON VALORES INICIALES MEDIANTE
EL MÉTODO DE EULER
En los problemas siguientes (3 y 4) use el método de Euler para obtener una aproximación a cuatro decimales
del valor indicado. Primero utilice h = 0.1 y despues utilice h = 0.05. Determine una solución explicita para
cada problema con valores iniciales y después construya tablas con los valores obtenidos.
Ejemplo 1. Ejercicios 2.6. Libro Dennis G. Zill (Problema 3)
2
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
y 0 = y, y(0) = 1, y(1.0)
Solución. Primer caso h = 0.1
Pasos:
i. Escribimos la ED en la forma:
dy
dx
= f (x; y), para extraer su segundo miembro
dy
=y
dx
ii. Denimos x0, y0 y h de acuerdo a los datos del problema
x0 = 0,
y0 = 1;
Para este primer caso: h = 0.1
iii. Planteamos la ecuación de Euler utilizando los datos iniciales:
y0+1 = y0 + hf (x0; y0)
y1 = y0 + h (y0)
y1 = 1 + (0.1)(1)
iv. Desarrollamos hasta el valor buscado en x, en este caso: x = 1.0.
y1 = 1 + (0.1)(1)
= 1 + 0.1
y1 = y(0.1) = 1.1
y1+1 = y1 + hf (x1; y1)
y2 = y1 + h (y0)
y2 = 1.1 + (0.1)(1.1)
= 1.1 + 0.11
y2 = y(0.2) = 1.21
y2+1 = y2 + hf (x2; y2)
y3 = y2 + h (y2)
y3 = 1.21 + (0.1)(1.21)
= 1.21 + 0.121
y3 = y(0.3) = 1.331
y3+1 = y3 + hf (x3; y3)
y4 = y3 + h (y3)
y4 = 1.331 + (0.1)(1.331)
= 1.331 + 0.1331
y4 = y(0.4) = 1.4641
y4+1 = y4 + hf (x4; y4)
y5 = y4 + h (y4)
y5 = 1.4641 + (0.1)(1.4641)
= 1.4641 + 0.14641
y5 = y(0.5) = 1.61051
y5+1 = y5 + hf (x5; y5)
y6 = y5 + h (y5)
y6 = 1.61051 + (0.1)(1.61051)
3
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
= 1.61051 + 0.16051
y6 = y(0.6) = 1.771561
y6+1 = y6 + hf (x6; y6)
y7 = y6 + h (y6)
y7 = 1.771561 + (0.1)(1.771561)
= 1.771561 + 0.1771561
y7 = y(0.7) = 1.9487171
y7+1 = y7 + hf (x7; y7)
y8 = y7 + h(y7)
y8 = 1.9487171 + (0.1)(1.9487171)
= 1.9487171 + 0.19487171
y8 = y(0.8) = 2.14358881
y8+1 = y8 + hf (x8; y8)
y9 = y8 + h (y8)
y9 = 2.14358881 + (0.1)(2.14358881)
= 2.14358881 + 0.214358881
y9 = y(0.9) = 2.357947
y9+1 = y9 + hf (x9; y9)
y10 = y9 + h (y9)
y10 = 2.357947 + (0.1)(2.357947)
= 2.357947 + 0.2357947
y10 = y(1.0) = 2.593741769
Solución. Segundo caso h = 0.05 para el mismo problema 3
Pasos:
i. Escribimos la ED en la forma:
dy
dx
= f (x; y), para extraer su segundo miembro
dy
=y
dx
ii. Denimos x0, y0 y h de acuerdo a los datos del problema
x0 = 0,
y0 = 1;
Para este segundo caso: h = 0.05
iii. Planteamos la ecuación de Euler utilizando los datos iniciales:
y0+1 = y0 + hf (x0; y0)
y1 = y0 + h (y0)
y1 = 1 + (0.05)(1)
iv. Desarrollamos hasta el valor buscado en x, en este caso: x = 1.0.
y1 = 1 + (0.05)(1)
= 1 + 0.05
y1 = y(0.05) = 1.05
y1+1 = y1 + hf (x1; y1)
y2 = y1 + h (y1)
y2 = 1.05 + (0.05)(1.05)
4
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Dynamic Systems Intelligence
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
= 1.05 + 0.0525
y2 = y(0.1) = 1.1025
y2+1 = y2 + hf (x2; y2)
y3 = y2 + h (y2)
y3 = 1.1025 + (0.05)(1.1025)
= 1.1025 + 0.055125
y3 = y(0.15) = 1.157625
y3+1 = y3 + hf (x3; y3)
y4 = y3 + h (y3)
y4 = 1.157625 + (0.05)(1.157625)
= 1.157625 + 0.05788125
y4 = y(0.2) = 1.21550625
y4+1 = y4 + hf (x4; y4)
y5 = y4 + h (y4)
y5 = 1.21550625 + (0.05)(1.21550625)
= 1.21550625 + 0.06077
y5 = y(0.25) = 1.276281563
y5+1 = y5 + hf (x5; y5)
y6 = y5 + h (y5)
y6 = 1.276281563 + (0.05)(1.276281563)
= 1.276281563 + 0.063814078
y6 = y(0.3) = 1.340095641
y6+1 = y6 + hf (x6; y6)
y7 = y6 + h (y6)
y7 = 1.340095641 + (0.05)(1.340095641)
= 1.340095641 + 0.067004
y7 = y(0.35) = 1.407100423
y7+1 = y7 + hf (x7; y7)
y8 = y7 + h (y7)
y8 = 1.407100423 + (0.05)(1.407100423)
= 1.407100423 + 0.070355021
y8 = y(0.4) = 1.477397321
y8+1 = y8 + hf (x8; y8)
y9 = y8 + h (y8)
y9 = 1.477397321 + (0.05)(1.477397321)
= 1.477397321 + 0.073869866
y9 = y(0.45) = 1.551267187
y9+1 = y9 + hf (x9; y9)
y10 = y9 + h (y9)
y10 = 1.551267187 + (0.05)(1.551267187)
= 1.551267187 + 0.073869866
y10 = y(0.5) = 1.628830546
y10 +1 = y10 + hf (x10 ; y10 )
y11 = y10 + h (y10 )
y11 = 1.628830546 + (0.05)(1.628830546)
5
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
= 1.628830546 + 0.081441527
y11 = y(0.55) = 1.710272073
y11 +1 = y11 + hf (x11 ; y11 )
y12 = y11 + h (y11 )
y12 = 1.7102272073 + (0.05)(1.7102272073)
= 1.7102272073 + 0.085513603
y12 = y(0.6) = 1.795785677
y12 +1 = y12 + hf (y12 )
y13 = y12 + h (y12 )
y13 = 1.795785677 + (0.05)(1.795785677)
= 1.795785677 + 0.08978
y13 = y(0.65) = 1.885574961
y13 +1 = y13 + hf (x13 ; y13 )
y14 = y13 + h (y13 )
y14 = 1.885574961 + (0.05)(1.885574961)
= 1.885574961 + 0.09427
y14 = y(0.7) = 1.979853709
y14 +1 = y14 + hf (x14 ; y14 )
y15 = y14 + h (y14 )
y15 = 1.979853709 + (0.05)(1.979853709)
= 1.979853709 + 0.098992685
y15 = y(0.75) = 2.078846394
y15 +1 = y15 + hf (x15 ; y15 )
y16 = y15 + h (y15 )
y16 = 2.078846394 + (0.05)(2.0788)
= 2.078846394 + 0.103942319
y16 = y(0.8) = 2.182788714
y16 +1 = y16 + hf (x16 ; y16 )
y17 = y16 + h (y16 )
y17 = 2.182788714 + (0.05)(2.182788714)
= 2.182788714 + 0.114570915
y17 = y(0.85) = 2.291418307
y17 +1 = y17 + hf (x17 ; y17 )
y18 = y17 + h (y17 )
y18 = 2.291418307 + (0.05)(2.291418307)
= 2.291418307 + 0.114570915
y18 = y(0.9) = 2.405989222
y18 +1 = y18 + hf (x18 ; y18 )
y19 = y18 + h (y18 )
y19 = 2.405989222 + (0.05)(2.405989222)
= 2.405989222 + 0.120299461
y19 = y(0.95) = 2.526288683
y19 +1 = y19 + hf (x19 ; y19 )
y20 = y19 + h (y19 )
y20 = 2.526288683 + (0.05)(y19 )
= 2.526288683 + 0.126314434
y20 = y(1.0) = 2.652603117
6
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Dynamic Systems Intelligence
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
El código en SAGE para resolver los problemas mediante métodos numéricos lo puedes ver en la presentación:
De donde sale el Método de Euler . da click aquí.
A continuación te dejo este mismo problema resuelto con SAGE. Si quieres aprender a editar la celda
de SAGE, revisa el siguiente artículo: Simulación, Gracación y Aplicación de Ecuaciones Diferenciales y
Sistemas Físicos can SAGE.
Algoritmo 1
### Metodo de Euler
def Euler(fun, a, b, N, y0):
h = (b - a)/N
x = [a]
y = [y0]
for k in range(N):
x.append(x[k]+h)
y.append(y[k]+(h)*fun(x[k], y[k]))
return zip(x, y)
##### Datos iniciales
x = var('x')
y = var('y')
f(x,y) = y
y0=1
a = 0.0
b = 1.0
## -> cambiar aquí la función f(x, y)
## Valor inicial en ý'
## Extremo inferior sobre 'x'
## Extremo superior sobre 'x'
##### Solución numérica para h=0.1
n = 10
## numero de pasos a modicar para ver aproximación
Euler_puntos=Euler(f, a, b, n, y0)
print 'Tabla para valores de h=0.1'
print table(Euler_puntos, header_row=["x", "y"], frame='true', align='center')
p0=line(Euler_puntos,color=(1,0,1), legend_label='$y\'(x)=y$')
show(p0,axes_labels=([r'$x$',r'$y = f(x)$']))
##### Solución numérica para h=0.05
n = 20
## numero de pasos a modicar para ver aproximación
Euler_puntos=Euler(f, a, b, n, y0)
print 'Tabla para valores de h=0.05'
print table(Euler_puntos, header_row=["x", "y"], frame='true', align='center')
p0=line(Euler_puntos,color=(1,0,1), legend_label='$y\'(x)=y$')
show(p0,axes_labels=([r'$x$',r'$y = f(x)$']))
-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:
-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:-:
Ejemplo 2. Ejercicios 2.6 Libro Dennis G. Zill (Problema 4)
y 0 = 2xy, y(1) = 1; y(1.5)
Solución. Primer caso h = 0.1
7
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
Pasos:
i. Escribimos la ED en la forma:
dy
dx
= f (x; y), para extraer su segundo miembro
dy
= 2xy
dx
ii. Denimos x0, y0 y h de acuerdo a los datos del problema
x0 = 1,
y0 = 1;
Para este primer caso: h = 0.1
iii. Planteamos la ecuación de Euler utilizando los datos iniciales:
y0+1 = y0 + hf (x0; y0)
y1 = y0 + h (2 x0 y0)
y1 = 1 + (0.1)(2(1)(1))
iv. Desarrollamos hasta el valor buscado en x, en este caso: x = 1.5.
y1 = 1 + (0.1)(2)
= 1 + 0.2
y1 = y(1.1) = 1.2
y1+1 = y1 + hf (x1; y1)
y2 = y1 + h (2 x1 y1)
y2 = 1.2 + (0.1)(2(1.1)(1.2))
= 1.2 + (0.1)(2.64)
= 1.2 + 0.264
y2 = y(1.2) = 1.464
y2+1 = y2 + hf (x2; y2)
y3 = y2 + h(2 x2 y2)
y3 = 1.464 + (0.1)(2(1.2)(1.464))
= 1.464 + (0.1)(3.5136)
= 1.464 + 0.35136
y3 = y(1.3) = 1.81536
y3+1 = y3 + hf (x3; y3)
y4 = y3 + h (2 x3 y3)
y4 = 1.81536 + (0.1)(2(1.3)(1.81536))
= 1.81536 + (0.1)(4.719936)
= 1.81536 + 0.4719936
y4 = y(1.4) = 2.2873536
y4+1 = y4 + hf (x4; y4)
y5 = y4 + h (2 x3 y3)
y5 = 2.2873536 + (0.1)(2(1.4)(2.2873536))
= 2.2873536 + (0.1)(6.40459008)
y5 = y(1.5) = 2.927812608
Solución. Segundo caso h = 0.05 para el mismo problema 4
Pasos:
i. Escribimos la ED en la forma:
dy
dx
= f (x; y), para extraer su segundo miembro
dy
= 2xy
dx
8
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Dynamic Systems Intelligence
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
ii. Denimos x0, y0 y h de acuerdo a los datos del problema
x0 = 1,
y0 = 1;
Para este segundo caso: h = 0.05
iii. Planteamos la ecuación de Euler utilizando los datos iniciales:
y0+1 = y0 + hf (x0; y0)
y1 = y0 + h (2 x0 y0)
y1 = 1 + (0.05)(2(1)(1))
iv. Desarrollamos hasta el valor buscado en x, en este caso: x = 1.5.
y1 = 1 + (0.05)(2)
= 1 + 0.1
y1 = y(1.05) = 1.1
y1+1 = y1 + hf (x1; y1)
y2 = y1 + h (2 x1 y1)
y2 = 1.1 + (0.05)(2(1.05)(1.1))
= 1.1 + (0.05)(2.31)
= 1.1 + 0.1155
y2 = y(1.1) = 1.2155
y2+1 = y2 + hf (x2; y2)
y3 = y2 + h (2 x2 y2)
y3 = 1.2155 + (0.05)(2(1.1)(1.2155))
= 1.2155 + (0.05)(2.6741)
= 1.2155 + 0.133705
y3 = y(1.15) = 1.349205
y3+1 = y3 + hf (x3; y3)
y4 = y3 + h(2 x3 y3)
y4 = 1.349205 + (0.05)(2(1.15)(1.349205))
= 1.349205 + (0.05)(3.1031715)
= 1.349205 + 0.155158575
y4 = y(1.2) = 1.504363575
y4+1 = y4 + hf (x4; y4)
y5 = y4 + h (2 x4 y4)
y5 = 1.504363575 + (0.05)(2(1.2)(1.5043))
= 1.504363575 + (0.05)(3.61047258)
= 1.504363575 + 0.18052
y5 = y(1.25) = 1.684887204
y5+1 = y5 + hf (x5; y5)
y6 = y5 + h (2 x5 y5)
y6 = 1.684887204 + (0.05)(2(1.25)(1.68488))
= 1.684887204 + (0.05)(4.21221801)
= 1.684887204 + 0.2106109
y6 = y(1.3) = 1.895498195
y6+1 = y6 + hf (x6; y6)
y7 = y6 + h (2 x6 y6)
y7 = 1.895498105 + (0.05)(2(1.3)(1.895498195))
9
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
= 1.895498105 + (0.05)(4.92829)
= 1.895498105 + 0.246414753
y7 = y(1.35) = 2.141912859
y7+1 = y7 + hF (x7; y7)
y8 = y7 + h (2 x7 y7)
y8 = 2.141912859 + (0.05)(2(1.35)(2.141912859))
= 2.141912859 + (0.05)(5.783164)
= 2.141912859 + 0.289158235
y8 = y(1.4) = 2.431071095
y8+1 = y8 + hf (x8; y8)
y9 = y8 + h (2 x8 y8)
y9 = 2.431071095 + (0.05)(2(1.4)(2.431071095))
= 2.431071095 + (0.05)(6.806999)
= 2.431071095 + 0.3403349
y9 = y(1.45) = 2.771421048
y9+1 = y9 + hf (x9; y9)
y10 = y9 + h (2 x9 y9)
y10 = 2.771421048 + (0.05)(2(1.45)(2.771421048))
= 2.771421048 + (0.05)(8.03712104)
= 2.771421048 + 0.401856052
y10 = y(1.5) = 3.1732771
El código en SAGE para resolver los problemas mediante métodos numéricos lo puedes ver en la presentación:
De donde sale el Método de Euler . da click aquí.
A continuación te dejo este mismo problema resuelto con SAGE. Si quieres aprender a editar la celda de
SAGE, revisa el siguiente artículo: Simulación, Gracación y Aplicación de Ecuaciones Diferenciales y
Sistemas Físicos can SAGE.
Algoritmo 2
### Metodo de Euler
def Euler(fun, a, b, N, y0):
h = (b - a)/N
x = [a]
y = [y0]
for k in range(N):
x.append(x[k]+h)
y.append(y[k]+(h)*fun(x[k], y[k]))
return zip(x, y)
##### Datos iniciales
x = var('x')
y = var('y')
f(x,y) = 2*x*y
y0= 1
a = 1.0
b = 1.5
## -> cambiar aquí la función f(x, y)
## Valor inicial en 'y'
## Extremo inferior sobre 'x'
## Extremo superior sobre 'x'
##### Solución numérica para h=0.1
10
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/
Dynamic Systems Intelligence
Alejandro Vivas Riverol
http://es.gravatar.com/adiutor
n=5
## numero de pasos a modicar para ver aproximación
Euler_puntos=Euler(f, a, b, n, y0)
print 'Tabla para valores de h=0.1'
print table(Euler_puntos, header_row=["x", "y"], frame='true', align='center')
p0=line(Euler_puntos,color=(1,0,1), legend_label='$y\'(x)=2xy$')
show(p0,axes_labels=([r'$x$',r'$y = f(x)$']))
##### Solución numérica para h=0.05
n = 10
## numero de pasos a modicar para ver aproximación
Euler_puntos=Euler(f, a, b, n, y0)
print 'Tabla para valores de h=0.05'
print table(Euler_puntos, header_row=["x", "y"], frame='true', align='center')
p0=line(Euler_puntos,color=(1,0,1), legend_label='$y\'(x)=2xy$')
show(p0,axes_labels=([r'$x$',r'$y = f(x)$']))
El código en MATHEMATICA para resolver mediante el método de euler para ecuaciones diferenciales es
el siguiente:
Algoritmo 3
Clear["Global'*"]
s4th = NDSolve[{y'[x] == 2.0 x y[x], y[1] == 1}, y, {x, 1, 1.5},
Method -> "ExplicitEuler", "StartingStepSize" -> 1/10];
t4th = Table[{h, y[h] /. s4th}, {h, 1, 1.5, 0.1}];
TableForm[t4th]
e4th = y[x] /. s4th[[1]];
Plot[e4th, {x, 1, 1.5}]
sol4th2 =
NDSolve[{y'[x] == 2.0 x y[x], y[1] == 1}, y, {x, 1, 1.5},
Method -> "ExplicitEuler", "StartingStepSize" -> 1/20];
t1h2 = Table[{i, y[i] /. sol4th2}, {i, 1, 1.5, 0.05}];
TableForm[t1h2]
eqn4th2 = y[x] /. sol4th2[[1]];
Plot[eqn4th2, {x, 1, 1.5}]
11
BLOG:
http://ecuaciondiferencialejerciciosresueltos.com/