Mathematical Methods for Engineering
Anuncio
Complex numbers
Graphic representation
Complex equations
Euler’s formula
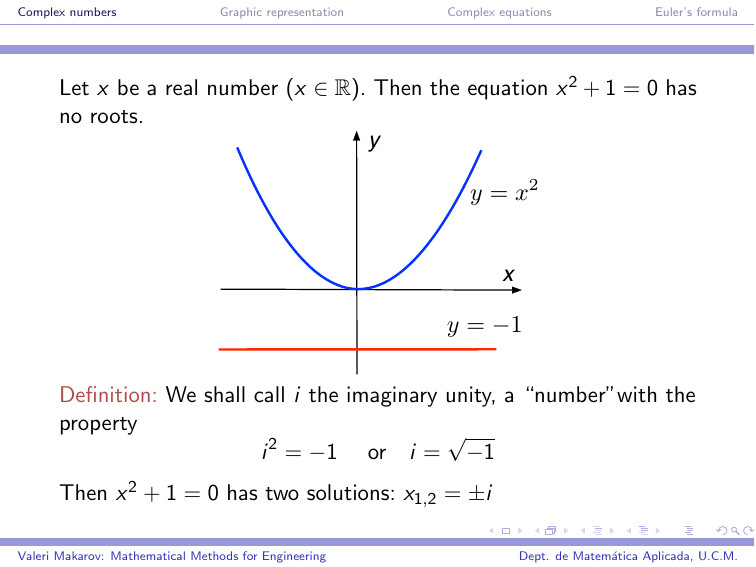
Let x be a real number (x 2 R). Then the equation x 2 + 1 = 0 has
no roots.
y
y = x2
x
y=
1
Definition: We shall call i the imaginary unity, a “number”with the
property
p
i 2 = 1 or i =
1
Then x 2 + 1 = 0 has two solutions: x1,2 = ±i
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Arithmetic operations
Addition and subtraction: (2 + 3i) + (4
Multiplication: (2 + 3i)(4
2i) = 8
2i) = 6 + i
6i 2 = 14 + 8i
4i + 12i
Important property: Let a, b 2 R, then
(a + ib)(a
ib) = a2 + b 2 2 R
Division:
2 + 3i
2 + 3i
4 + 2i
(2 + 3i)(4 + 2i)
1
4
=
⇥
=
=
+ i
4 2i
4 2i
4 + 2i
16 + 4
10 5
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Definition: A complex number z is a number that can be
expressed in the form z = a + bi (a, b 2 R).
z 2 C = {a + ib : a, b 2 R}
where C denotes the set of all complex numbers.
A complex number is a pair of two real numbers C = R2
Definition: The complex conjugate of a complex number
z = a + ib is defined to be
z =a
bi
Test: Prove: z ⇥ z = a2 + b 2
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Graphic representation
z = a + bi = r (cos(') + i sin('))
(z)
z2C
b
r
'
a
<(z)
8
< arctan(b/a)
p
2
2
arctan(b/a) + ⇡
r = a + b , ' = arctan 2(b, a) =
:
arctan(b/a) ⇡
Valeri Makarov: Mathematical Methods for Engineering
if a > 0
if a < 0, b
if a, b < 0
0
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Euler’s formula
e i' = cos(') + i sin(')
From trigonometric to exponential representation:
z = r (cos(') + i sin(')) = re i'
p
p
|z| = z z = r = a2 + b 2 is called absolute value or modulus
' is called argument or phase (tan(') = b/a)
Problem 1: Find the absolute value and phase of
b) (3 + 4i)
1
1
3 4i
z=
=
) |z| =
3 + 4i
9 + 16
Valeri Makarov: Mathematical Methods for Engineering
p
9 + 16
1
= ; tan(') =
25
5
4
3
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Sum of two complex numbers can be interpreted as a point in the
complex plane obtained by addition of two vectors
(z)
u
u+
v
v
<(z)
u = a + bi; v = c + di ) u + v = (a + c) + (b + d)i
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Problem 2a: Draw a set verifying |z| < 1 <(z).
p
x2 + y2 < 1 x
We have: 1
x > 0 or x < 1. Squaring both sides:
x2 + y2 < 1
2x + x 2 ) x <
y2
1
2
(z)
1/2
<(z)
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Problem 2c: Draw a set verifying
z 3
=2
z +3
We have |z
3| = 2|z + 3|. Squaring |z
(x
3|2 = 4|z + 3|2 or
3)2 + y 2 = 4((x + 3)2 + y 2 )
(z)
4
-5
Valeri Makarov: Mathematical Methods for Engineering
<(z)
Dept. de Matemática Aplicada, U.C.M.
Complex numbers
Graphic representation
Complex equations
Euler’s formula
Some properties of complex numbers
Problem 3: a) |z| = |z |; b) z = z; c) z + w = z + w
These are obvious.
d) zw = z w
(a + bi)(c + di) = (ac
(a + bi )(c + di ) = (a
f) z
1
= (z )
bd) + (ad + bc)i = (ac bd) (ad+bc)i
bi)(c
di) = (ac
bd)
(ad + bc)i
1
✓ ◆
✓ ◆
1
z
z
z
1
=
= 2 =
=
z
zz
|z|
zz
z
Valeri Makarov: Mathematical Methods for Engineering
Dept. de Matemática Aplicada, U.C.M.