Document
Anuncio

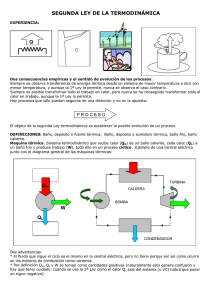
5_2ª LEY DE LA TERMODINÁMICA 5.1 DIRECCIÓN DE LOS PROCESOS 5.2 FOCOS, DEPÓSITOS O BAÑOS 5.3 MÁQUINAS TÉRMICAS 5.4 REFRIGERADORES Y BOMBAS DE CALOR 5.5 PROCESOS REVERSIBLES Y PROCESOS IRREVERSIBLES 5.6 CICLO DE CARNOT 5.7 ESCALA TERMODINÁMICA DE TEMPERATURAS 5.8 MÁQUINA TÉRMICA DE CARNOT 5.1 DIRECCIÓN TEMPORAL DE LOS PROCESOS EXPERIENCIA: Q Dos consecuencias empíricas y el sentido de evolución de los procesos: T baja T PROCESO PROCESO T alta T W T T baja Q T T alta W Q ¡¡¡ Hay procesos que sólo pueden seguirse en una dirección y no en la opuesta !!! ¡¡¡ AUNQUE LO PERMITA LA PRIMERA LEY DE LA TERMODINÁMICA !!! El objeto de la segunda Ley termodinámica es establecer la posible evolución de un proceso. 5.2 FOCOS, DEPÓSITOS O BAÑOS DEFINICIONES: Baño, depósito o foco: Sistema capaz de intercambiar energía térmica sin modificar su temperatura. Los baños, depósitos o focos se llaman fuentes o sumideros dependiendo de si suministran o adsorben energía. Por su definición los baños, depósitos o focos deberían son sistemas de gran tamaño o gran capacidad calorífica. También son baños, depósitos o focos artilugios que en alguna forma se mantienen a temperatura constante como los hornos. También son baños, depósitos o focos los sistemas que sin ser grandes puede considerase como tales de forma relativa. 5.3 MÁQUINAS TÉRMICAS MAQUINA TÉRMICA ⇒proceso cíclico Ejemplo de una central eléctrica QH QH CALDERA BOMBA TURBINA W QL W CONDENSADOR QL Dos advertencias: * El fluido que sigue el ciclo es el mismo en la central eléctrica, pero no tiene porque ser así como ocurre en los motores de combustión como veremos más adelante. * Por definición QH, QL y W se toman como cantidades positivas ∆U = Q − W = (QH − QL ) − W CICLO: W = QH − QL ∆U = Q − W = (QH − QL ) − W RENDIMIENTO η= CICLO: W = QH − QL QH Q − QL Q Energía _ Deseada W = = H = 1− L Coste _ Energético QH QH QH ¡¡¡QL ≠ 0!!! ORIGEN DE LA PÉRDIDA DE QL QL ⇒η <1 FRICCIÓN técnicamente evitable. 2a LEY: desgraciadamente INEVITABLE → Enunciado de Kelvin-Planck de la 2ª Ley: Es imposible para cualquier máquina térmica recibir calor de un baño caliente, producir trabajo y no ceder nada de calor a un baño frío. η =1 QH W W 5.4 REFRIGERADORES Y BOMBAS DE CALOR “máquinas térmicas en sentido opuesto” QH W + QL = QH QH > QL Refrigerador y bomba de calor. COPR = QL 120kPa -25ºC 120kPa -20ºC CONDENSADOR → Coeficientes de OPeración: Energía _ Deseada QL 1 = = Coste _ Energético W QH / QL − 1 COPBC = 800kPa 60ºC COMPRESOR VÁLVULA W Rendimiento η EVAPORADOR 800kPa 30ºC Energía _ Deseada QH 1 = = Coste _ Energético W 1 − QL / QH COPR > 0 COPBC = COPR + 1 COPBC > 1 →Enunciado de la 2ª Ley de Clausius: Es imposible para cualquier máquina térmica recibir calor de un baño frío y cederlo a un baño caliente sin gasto de trabajo. QH QL COPR = ∞ COPBC = ∞ Coeficiente de Eficiencia Energética Refrigeradores y acondicionadores de aire: COPR = Energía _ Deseada QL 1 = = Coste _ Energético W QH / QL − 1 Coeficiente de Eficiencia Energética (USA): Energía térmica: COPR → CEE = Btu (British thermal unit) = 1.055 kJ 1Wh = 1J / s × 3600 s = 3600 J = COPR = 1 = 1kWh → CEE = 3.412 1kWh Valores usuales: COPR → 2-4 Valores usuales: COPBC → 2-3 o QL ( Btu ) W (Vatios − hora ) CEE → 8-12 1Btu 3600 J = 3.412 Btu 1055 J Enunciado de Clausius: Es imposible para cualquier máquina térmica recibir calor de un baño frío y cederlo a un baño caliente sin gasto de trabajo. Enunciado de Kelvin-Planck: Es imposible para cualquier máquina térmica recibir calor de un baño caliente, producir trabajo y no ceder nada de calor a un baño frío. QH QH W QL Equivalencia entre los dos enunciados: TH QH QH+QL W=QH η=100% QL TL ≡ QL QL Enunciado de Clausius: Es imposible para cualquier máquina térmica recibir calor de un baño frío y cederlo a un baño caliente sin gasto de trabajo. Enunciado de Kelvin-Planck: Es imposible para cualquier máquina térmica recibir calor de un baño caliente, producir trabajo y no ceder nada de calor a un baño frío. QH QH QL W Equivalencia entre los dos enunciados: QL QL ≡ QH QL QH-QL QL QL W TL Movimientos perpetuos de primera y segunda especie: máquinas que violan el primer o el segundo principio de la termodinámica 5.5 PROCESOS REVERSIBLES Y PROCESOS IRREVERSIBLES PROCESOS REVERSIBLES: LOS QUE SE RECORREN A TRAVÉS DE SUCESIVOS ESTADOS DE EQUILIBRIO Y QUE POR TANTO SE PUEDEN VOLVER A RECORRER EN SENTIDO OPUESTO A TRAVÉS DE ESOS MISMOS ESTADOS DE EQUILIBRIO, TANTO DEL SISTEMA COMO DEL RESTO DEL UNIVERSO. IRREVERSIBLES: LOS QUE NO SON REVERSIBLES. Observaciones •No olvide que siempre tenemos el sistema y el resto del universo. •Ningún proceso real es reversible. •La irreversibilidad suele estar ligada a la violencia del proceso y exigen mayor cantidad de trabajo (cuando lo damos) o generan menor cantidad de trabajo (cuando lo recibimos) !siempre en contra nuestra! Reducen el rendimiento de cualquier dispositivo termodinámico. •Los procesos reversibles son infinitamente lentos. El proceso pasa por sucesivos estados de equilibrio los cuales, estrictamente, se alcanzan en un tiempo infinito. •Los procesos irreversibles también pueden ser lentos. TH A I S L A N T E TL < TH •Un sistema puede volver al estado inicial en un proceso irreversible PERO el resto del universo, inevitablemente, ha cambiado. P P SISTEMA • RESTO UNIVERSO V V •En un proceso irreversible puede ocurrir que el proceso seguido por el sistema que estamos estudiando haya pasado por sucesivos estados de equilibrio, entonces es posible recorrerlos en sentido opuesto para volver al estado inicial (y no el resto del universo); estos procesos se llaman internamente reversibles, el proceso sigue siendo irreversible. P SISTEMA P • RESTO UNIVERSO • V V •En un proceso irreversible puede ocurrir que el proceso seguido por el resto del universo haya pasado por sucesivos estados de equilibrio, entonces es posible recorrerlos en sentido opuesto para volver al estado inicial (y no el sistema); estos procesos se llaman externamente reversibles, el proceso sigue siendo irreversible. (Los baños suelen verificar esta condición). •Hay procesos que son a la vez internamente y externamente reversibles y aún son procesos totalmente irreversibles. (Un ejemplo es el caso mencionado de la transferencia de energía térmica entre dos sistemas con un aislante). •Podemos tratar de hacer los procesos “lo menos irreversibles” posible; en los procesos reversibles es relativamente fácil evaluar cualquier variable termodinámica, sirven para compararlos con los sistemas reales y sacar consecuencias para mejorar el rendimiento de estos. •El procedimiento para hacer a un proceso reversible es realizar lentamente trabajo (proceso cuasi-estático) y disponer de muchos baños térmicos para hacer los intercambios de calor poco a poco. Un proceso estrictamente reversible necesita producir trabajo de una manera infinitamente lenta y disponer de infinitos baños térmicos. •En principio se podría tender a mejorar los rendimientos haciendo los sistemas “más reversibles” pero, además de los problemas técnicos, la potencia sería cada vez menor. •No olvide nunca que las propiedades de un estado termodinámico no dependen de cómo se haya alcanzado ese estado, sea mediante un proceso reversible o un proceso irreversible. 1 2 5.6 CICLO DE CARNOT 2 3 3 TH 4 4 TL TH TH TL TL QL QH P ● QH TH 2 ● W 4 Q = ∫ TdS T W = ∫ pdV 1 1 ● TL 3 ● QH 2 Q TH QL 1 TL V 4 QL 3 S P T 1 QH TH 2 TH W 4 QH 1 Q TL QL 3 2 TL QL 4 V 3 S Observaciones: TH TH Ciclo reversible por definición W = W12 + W23 + W34 + W41 Q = QH − QL Q =W W + QL = QH TL Máquina Térmica TL Refrigerante Bomba de calor Principios de Carnot: Todas las maquinas térmicas que sigan un proceso reversible entre los mismos baños térmicos tienen igual rendimiento. El rendimiento de una máquina térmica que siga un proceso irreversible entre dos baños térmicos es menor que el rendimiento de cualquier máquina térmica que siga un proceso reversible entre los dos mismos baños TH QH QH -QH W(I)-W(R) W(R) IRREV W(I) QL(I)<QL(R) REV -W(R) QL(R) -QL(R) TL QL(I)-QL(R) TL η REV > η IRR 5.7 ESCALA TERMODINÁMICA DE TEMPERATURAS 1er. Principio de Carnot T1 Q1 W QH − QL Q = = 1− L QH QH QH ⇒ Q1 = f (T1 , T2 ) Q2 Q1 Q2 T2 Q2 Q3 η= Q1 Q2 Q3 = Q2 Q3 Q1 ⇒ η REV = η (TH , TL ) ⇒ QH = f (TH , TL ) QL Q3 Q2 = f (T2 , T3 ) = f (T3 , T1 ) Q3 Q1 ⇒ f (T1 , T2 ) f (T2 , T3 ) = f (T3 , T1 ) Q3 ⇒ f (Ta , Tb ) = T3 KELVIN → F (Ta ) F (Tb ) F (Ta ) Ta = F (Tb ) Tb ⇒ Qa F (Ta ) = Qb F (Tb ) Qa Ta = Qb Tb Además se ha impuesto que el punto triple del agua (0.01ºC) le correspondan 273.16K, así 1K=1ºC y T(ºC)=T(K)-273.15 5.8 η= MÁQUINA TÉRMICA DE CARNOT W QH − QL Q = = 1− L QH QH QH = 1− TL TH Para una máquina de Carnot O cualquier otra REVERSIBLE General η REV > η IRR (1 − QL T Q ) REV = 1 − L = η REV > η IRR = (1 − L ) IRR QH TH QH CALIDAD Y DEGRADACIÓN DE LA ENERGÍA: TH≈TL QH TH>>TL TH-TL pequeño ⇓ η pequeño ⇓ QH de poca calidad TH-TL grande ⇓ η grande ⇓ QH de gran calidad TL LIMITES DE LOS COPs QH TL 1 1 < QH / QL − 1 TH / TL − 1 1 1 COPBC = < 1 − QL / QH 1 − TL / TH COPR = MÁQUINA TÉRMICA (Cíclica) RESUMEN Definición : E _ útil Eficiencia = E _ consumida QH REFRIGERADOR O BOMBA DE CALOR (Cíclica) QH Eficiencia = η ,COP,... W QL W QL 1ª Ley: W = QH − QL REVERS : η= W Q T = 1− L ≤ 1− L QH QH TH QL TL = QH TH COPR = QL 1 1 = ≤ W QH / QL − 1 TH / TL − 1 COPBC = QH 1 1 = ≤ W 1 − QL / QH 1 − TL / TH Ejemplo 15 MAQUINA TÉRMICA: η=24% Potencia=48.47 kW Valor calorífico del combustible = 44191 kJ/kg PREGUNTA: ¿consumo (kg/seg)? QH • Consumo = m W QL • • QH = m× ValorCalorífico • • • m = QH / ValorCalorifico = QH / 44191kJ / kg • η= W W = • QH QH • QH = • W η = ... = 202.2kW Consumo = ... = 16.47kg / hora Ejemplo 16 BOMBA DE CALOR de COP=2.5, Tcasa 20ºC, T exterior -2ºC Pérdidas en la casa 80000kJ/hora • Q' = 80000kJ / hora Tcalle = −2º C Tcasa = 20º C PREGUNTAS: ¿potencia? ¿QL? • COP = • QH QH = • W W • • • W= • QH Q' = ... = 8.9kW COP COP • QL = QH − W = ... = 48000kJ / hora PREGUNTA: ¿Qué pasaría si la bomba fuera reversible? 1 1 Q = = 13.3 COP = H = ... = 1 − QL / QH 1 − TL / TH W • W= • • QH Q' = ... = 1.67 kW COP COP PREGUNTA: ¿Qué pasaría si se hubiese utilizado un calentador eléctrico? • Q' = 80000kJ / hora Tcalle = −2º C Tcasa = 20º C • Energía _ Deseada QH Q = = 1 = •H Coste _ Energético W W • W= • • QH Q' = ... = 22.2kW 1 1 Ejemplo 17 MAQUINA DE CARNOT (TÉRMICA): TH=652ºC PREGUNTA: ¿Rendimiento? ¿QL? QH=500kJ La máquina de Carnot es reversible: W QL η= W Q T = 1− L = 1− L QH QH TH TL=30ºC QL = QH TL TH = ... = 0.672 = ... = 163.7 kJ PREGUNTA: ¿Qué pasa con el rendimiento si bajamos la temperatura del foco caliente? (TL fija) η 1 TL TH Ciclo Carnot http://www.sc.ehu.es/sbweb/fisica/estadistica/carnot/carnot.htm SecondLaw Brig Klyce http://www.panspermia.org/seconlaw.htm#whatsnew Carnot Cycle (Heat Engine) http://www.phy.ntnu.edu.tw/java/carnot/carnot.html http://137.229.52.100/physics/p103/applets/cp_carnot.html http://www.mhhe.com/physsci/physical/jones/graphics/jones2001phys_s/ch13/ot hers/13-3/index.html