El número oculto II profesor

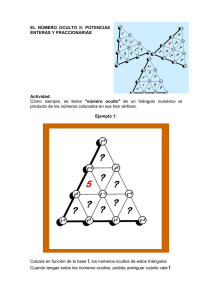
EL NÚMERO OCULTO II: POTENCIAS ENTERAS Y FRACCIONARIAS
Observaciones:
Después de haber trabajado las operaciones con potencias de exponentes
naturales, en "El número oculto I", se debe pasar a generalizarlas al caso de
las potencias con exponentes enteros e incluso potencias con exponentes
fraccionarios.
Para consolidar estas operaciones, se propone una actividad con tres ejemplos
crecientes en dificultad. Los alumnos ya han trabajado con los "números
ocultos" en la actividad anterior, dedicada a operaciones con potencias de
exponentes números naturales.
En el ejemplo 1, los alumnos deben, para obtener los "números ocultos",
multiplicar potencias de igual base, pero con exponentes enteros, colocadas en
los tres vértices de los triángulos. Se trata del ejemplo más sencillo
En el ejemplo 2, los estudiantes deberán en algunos casos también dividir
potencias de igual base para obtener los contenidos de algunas casillas que
aparecen con un punto de interrogación. Al efectuar la división de potencias de
igual base con exponentes enteros, los alumnos suelen frecuentemente
cometer errores cuando el exponente del divisor es negativo, olvidándose de
que al restar ese exponente del exponente del numerador, se debe en realidad
sumar los exponentes. Por eso, este tipo de ejercicios puede ayudar a evitar
este error.
En el ejemplo 3, se trata de la misma actividad pero con potencias de
exponentes fraccionarios.
Nivel: 2º- 3º-4º de ESO
Actividad:
Cómo siempre, se llama "número oculto" de un triángulo numérico al
producto de los números colocados en sus tres vértices.
Ejemplo 1:
Calcula en función de la
base t, los números
ocultos de estos triángulos
Cuando tengas todos los
números ocultos, podrás
averiguar cuánto vale t
Ejemplo 2:
En este nuevo ejemplo, los números también vienen expresados en función de
la base a, pero en algunos casos han desaparecidos los números de las
casillas, y en otros los números ocultos de los triángulos.
Aplicando las propiedades
de las potencias, expresa
en función de la base a,
todos los contenidos que
aparecen con un punto de
interrogación.
Ejemplo 3
Este último ejemplo, hace
aparecer
exponentes
fraccionarios. La única pequeña
dificultad añadida es pues
trabajar con fracciones en lugar
de con números enteros.
SOLUCIONES
Ejemplo 1:
Ejemplo 2:
Ejemplo 3: