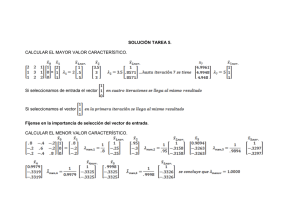
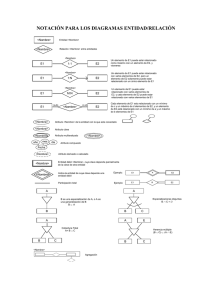
Implementación de support vector machines para reconocimiento
Anuncio

UNIVERSIDAD SIMÓN BOLÍVAR
Decanato de Estudios Profesionales
Coordinación de Ingeniería Electrónica
IMPLEMENTACIÓN DE SUPPORT VECTOR MACHINES PARA
RECONOCIMIENTO DE SEGMENTOS DE LA POBLACIÓN
Por
Rubén Alfredo Marrero Guerrero
Sartenejas, Noviembre de 2005
UNIVERSIDAD SIMÓN BOLÍVAR
Decanato de Estudios Profesionales
Coordinación de Ingeniería Electrónica
IMPLEMENTACIÓN DE SUPPORT VECTOR MACHINES PARA
RECONOCIMIENTO DE SEGMENTOS DE LA POBLACIÓN
Por
Rubén Alfredo Marrero Guerrero
Realizado con la Asesoría de
Ing. Gerardo Fernández
Ing. Samuel Cohen
INFORME FINAL DE GRADO
Presentado ante la Ilustre Universidad Simón Bolívar
como requisito parcial para optar al título de Ingeniero Electrónico
Sartenejas, Noviembre de 2005
UNIVERSIDAD SIMÓN BOLÍVAR
Decanato de Estudios Profesionales
Coordinación de Ingeniería Electrónica
IMPLEMENTACIÓN DE SUPPORT VECTOR MACHINES PARA
RECONOCIMIENTO DE SEGMENTOS DE LA POBLACIÓN
INFORME FINAL DE GRADO presentado por
Rubén Alfredo Marrero Guerrero - Carnet: 0033035
REALIZADO CON LA ASESORIA DE: Ing. Gerardo Fernández, Ing. Samuel Cohen
RESUMEN
Este proyecto fue realizado en la sede principal de Procter & Gamble Servicios
Latinoamérica con la finalidad de explorar el potencial de Support Vector Machines como
herramienta en la identificación de segmentos de la población basados en patrones de
consumo y características psicográficas. Inicialmente se llevó a cabo una investigación sobre
ésta herramienta y técnicas de Minería de Datos. Se contó con una base de datos de los
resultados de un estudio realizado sobre la población mexicana, el cual fue utilizado como
base para la segmentación a través de Agrupamiento, seguido de una reducción de parámetros
con un análisis de Componentes Principales. Los parámetros resultantes fueron utilizados
como señales de entrada en la creación de modelos de Support Vector Machines, alcanzando
un promedio de validación cruzada superior al 99% de efectividad, luego de iterar en la
creación de un espacio característico que separase los datos. Dicho resultado se obtuvo con un
espacio característico resultante de una regresión con normalización exponencial, empleando
el Kernel RBF con parámetros de generalización gamma=100 y de dispersión sigma=0,4. Se
concluyó que Support Vector Machines proporciona excelentes resultados en ésta aplicación,
aunque se evidenció el rol protagónico de los espacios característicos, los cuales no poseen un
estándar para su creación.
PALABRAS CLAVES: Support Vector Machines, Minería de Datos, Inteligencia
Artificial, Aprendizaje Automático.
Sartenejas, Noviembre de 2005
i
ÍNDICE GENERAL
CAPÍTULO 1: INTRODUCCIÓN..............................................................................................1
CAPÍTULO 2: DESCRIPCIÓN DE LA EMPRESA ..................................................................3
2.1 RESEÑA HISTÓRICA .....................................................................................................3
2.2 PROPÓSITO .....................................................................................................................5
2.3 VALORES Y PRINCIPIOS ..............................................................................................5
2.4 ESTRUCTURA ORGANIZACIONAL ............................................................................6
CAPÍTULO 3: OBJETIVOS .......................................................................................................8
3.1 OBJETIVOS GENERALES .............................................................................................8
3.2 OBJETIVOS ESPECÍFICOS ............................................................................................8
CAPÍTULO 4: MARCO TEÓRICO ...........................................................................................9
4.1 MÁQUINAS DE APRENDIZAJE....................................................................................9
4.2 MINERÍA DE DATOS ...................................................................................................12
4.2.1 Técnicas ....................................................................................................................13
4.2.1.1 Agrupamiento ....................................................................................................14
4.2.1.2 Componentes Principales ..................................................................................16
4.3 SUPPORT VECTOR MACHINES.................................................................................17
4.3.1 Clasificadores Lineales.............................................................................................17
4.3.2 Dominios característicos y Kernels ..........................................................................22
4.3.3 Teoría de Generalización..........................................................................................25
4.3.4 Teoría de Optimización ............................................................................................28
4.3.5 Clasificadores Support Vector..................................................................................29
4.3.6 Aplicaciones de Support Vector Machines ..............................................................32
4.4 MERCADEO...................................................................................................................32
CAPÍTULO 5: MARCO METODOLÓGICO ..........................................................................35
5.1 REVISIÓN BIBLIOGRÁFICA.......................................................................................35
5.2 DESARROLLO DEL PROYECTO................................................................................35
5.2.1 Entendimiento del negocio .......................................................................................36
5.2.2 Entendimiento de los datos.......................................................................................37
ii
5.2.3 Preparación de los datos ...........................................................................................38
5.2.4 Modelado ..................................................................................................................38
5.2.5 Evaluación ................................................................................................................39
5.2.6 Despliegue ................................................................................................................39
CAPÍTULO 6: SOFTWARE UTILIZADO ..............................................................................40
6.1 MATLAB ........................................................................................................................40
6.1.1 LS-SVM toolbox ......................................................................................................41
6.2 SPSS ................................................................................................................................42
6.3 QUANVERT ...................................................................................................................43
CAPÍTULO 7: RESULTADOS OBTENIDOS.........................................................................45
7.1 REVISION BIBLIOGRAFICA.......................................................................................45
7.2 DESARROLLO DEL PROYECTO................................................................................45
7.2.1 Entendimiento del negocio .......................................................................................45
7.2.2 Entendimiento de los datos.......................................................................................48
7.2.3 Preparación de los datos ...........................................................................................51
7.2.4 Modelado ..................................................................................................................58
7.2.5 Evaluación ................................................................................................................69
7.2.6 Despliegue ................................................................................................................70
CAPÍTULO 8: CONCLUSIONES Y RECOMENDACIONES ...............................................71
CAPÍTULO 9: REFERENCIAS BIBLIOGRÁFICAS .............................................................73
iii
ÍNDICE DE TABLAS
Tabla 7.1 Matriz de componentes para cada conglomerado (primeros 30 atributos)................56
Tabla 7.2 Componentes de los atributos seleccionados para cada conglomerado ....................57
Tabla 7.3 Matriz de correlaciones bivariadas (Continuación)...................................................58
Tabla 7.4 Componentes de los atributos para cada conglomerado............................................60
Tabla 7.5 Resultados de la validación cruzada para el Kernel RBF con espacio característico
de regresión con normalización exponencial.............................................................................69
iv
ÍNDICE DE FIGURAS
Figura 2.1 Valores de Procter & Gamble ....................................................................................5
Figura 4.1 Un sistema de Inteligencia Artificial .......................................................................10
Figura 4.2 Métodos de medición de distancia entre datos.........................................................15
Figura 4.3 Ejemplo de Dendograma..........................................................................................16
Figura 4.4 Hiperplano (w, b) separando una data de entrenamiento bidimensional .................18
Figura 4.5 Márgenes para dos puntos para un hiperplano.........................................................19
Figura 4.6 Margen del conjunto de entrenamiento....................................................................20
Figura 4.7 Margen estacionario de dos puntos ..........................................................................20
Figura 4.8 Ejemplo del uso de dominios característicos ...........................................................22
Figura 4.9 Ejemplo de RBF unidimensional .............................................................................25
2
Figura 4.10 Tres puntos en R quebrantados por líneas orientadas .........................................26
Figura 4.11 Ejemplo de Clasificadores Support Vector para cierta data de entrenamiento......30
Figura 4.12 Estimación del error de clasificación con la técnica “Holdout” ............................31
Figura 4.13 Estimación del error de clasificación con la técnica de validación cruzada ..........31
Figura 4.14 Posicionamiento por calidad versus precio percibido............................................34
Figura 5.1 Fases del modelo de referencia CRISP-DM ............................................................36
Figura 6.1 Ejemplo de vista del programa MATLAB...............................................................40
Figura 6.2 Ejemplo de clasificación binaria con toolbox LS-SVM ..........................................41
Figura 6.3 Ejemplo de vista de datos con valores categóricos y escalares en SPSS .................42
Figura 6.4 Ejemplo de vista del programa Quanvert.................................................................44
Figura 7.1 Estadísticos descriptivos de los datos disponibles (primeros 7 atributos) ...............50
Figura 7.2 Dendograma de los datos (parte final) .....................................................................52
Figura 7.3 Resultados del agrupamiento K-promedios No. 1 ...................................................53
Figura 7.4 Resultado del agrupamiento K-promedios No. 2.....................................................53
Figura 7.5 Centros de cada conglomerado para cada atributo evaluado (primeros 9) ..............54
Figura 7.6 Pertenencia a los conglomerados de cada fuente de datos (primeros 30) ................55
Figura 7.7 Resultados obtenidos con distintos Kernel y parámetros sobre los datos de prueba59
v
Figura 7.8 Distribución de los datos en el espacio característico de componentes principales61
Figura 7.9 Resultados obtenidos con espacio característico de componentes principales con
distintos Kernel y parámetros sobre los datos de prueba ..........................................................62
Figura 7.10 Distribución de los datos en el espacio característico de componentes principales
con normalización lineal a 1......................................................................................................63
Figura 7.11 Distribución de los datos en el espacio característico de componentes principales
con normalización exponencial a 1 ...........................................................................................63
Figura 7.12 Distribución de los datos en el espacio característico de regresión lineal ............65
Figura 7.13 Resultados obtenidos con espacio característico de regresión con distintos Kernel
y parámetros sobre los datos de prueba .....................................................................................66
Figura 7.14 Distribución de los datos en el espacio característico de regresión lineal con
normalización exponencial ........................................................................................................67
Figura 7.15 Resultados obtenidos con espacio característico de regresión con normalización
exponencial para distintos Kernel y parámetros sobre los datos de prueba ..............................68
vi
GLOSARIO
Agrupamiento: técnica de Minería de Datos que busca definir grupos con características
similares.
Aprendizaje Automático: es una rama de la Inteligencia Artificial cuyo objetivo es
desarrollar técnicas que permitan a las computadoras aprender.
Atributos: grupo de datos que representan las entradas que alimentan una Máquina de
Aprendizaje.
Capacidad: habilidad de una Máquina de Aprendizaje de aprender de la data de
entrenamiento sin ningún error.
Clasificador Lineal: aquel cuya frontera de decisión es determinada por una función lineal.
Componentes Principales: técnica de Minería de Datos cuyo fin es la síntesis de
información, o reducción de la dimensión (número de variables).
CRISP-DM: Proceso Estándar para Minería de Datos en Industrias Varias (Cross Industry
Standard Process for Data Mining). Modelo de referencia para el desarrollo de proyectos de
Minería de Datos.
Dimensión VC (Vapnik Chervonenkis): para un grupo de funciones se define como el
número máximo de puntos de entrenamiento que pueden ser quebrantados por las mismas.
Dominios o Espacios Característicos: representación alternativa de los datos a través de la
transformación de las variables o atributos de un dominio a otro.
Generalización: capacidad de una Máquina de Aprendizaje de clasificar de forma correcta
datos distintos a los contenidos en la data de entrenamiento, a través de la flexibilización de
sus fronteras de decisión.
Inteligencia Artificial (IA): inteligencia exhibida por artefactos creados por humanos, es
decir, artificial.
Kernel: representación dual del producto interno de los atributos originales de un clasificador
lineal que contiene implícito un dominio característico.
Máquinas de Aprendizaje: área de investigación que desarrolla de métodos y algoritmos que
permiten a un sistema computarizado tomar decisiones en base a experiencias pasadas.
vii
Margen: para un punto específico como la distancia mínima de dicho punto al hiperplano o
frontera de decisión.
Mercadeo: toda acción que promueve una actividad, desde la concepción de la idea, hasta el
momento en que el producto o servicio es adquirido por los clientes.
Metodología del Aprendizaje: técnica de usar ejemplos en el entrenamiento de una máquina
para la obtención de un programa que resuelva un problema planteado.
Minería de Datos: proceso analítico diseñado para explorar grandes volúmenes de datos con
el objeto de descubrir patrones y modelos de comportamiento o relaciones entre diferentes
variables.
Support Vector Machines: algoritmo de Aprendizaje Automático que permite la
clasificación binaria de datos, a través de clasificadores lineales que actúan sobre mapeos no
lineales, a espacios característicos n-dimensionales.
CAPÍTULO 1: INTRODUCCIÓN
En las últimas décadas, la evolución de las computadoras y su masificación a nivel
global, han permitido el desarrollo de una gran cantidad de recursos tecnológicos que
proporcionan herramientas para la optimización de casi cualquier proceso. El Aprendizaje
Automático, como rama de la Inteligencia Artificial, ha tomado auge en los últimos años
gracias a dicha evolución, proponiendo metodologías muy distintas a las técnicas de
programación tradicionales. Debido a la naturaleza de la Metodología del Aprendizaje
utilizada en el Aprendizaje Automático, en la que se le “enseña” a la máquina a través de
ejemplos, el número de posibles aplicaciones promete ser muy amplio.
Support Vector Machines surge como un algoritmo de Aprendizaje Automático
alternativo, ofreciendo características de generalización y optimización robustas. Debido a su
reciente desarrollo, sus aplicaciones probadas son escasas, y en su mayoría experimentales.
El mercadeo constituye actualmente un elemento fundamental en el comercio, y la
investigación de mercado se ha convertido en una herramienta primordial en la optimización
de recursos invertidos en sus actividades. Una de sus funciones es enfocar los esfuerzos
(inversión) en un grupo de la población con características específicas para aumentar la
eficacia, pero dicho grupo, al no estar aislado no puede ser identificado con facilidad de forma
consistente.
La necesidad de la identificación consistente de un segmento de la población con
características determinadas, que permitiese realizar estudios de mercado para entender, y en
lo posible satisfacer sus necesidades, llevó a la búsqueda de soluciones inteligentes. En ésta
búsqueda, Support Vector Machines surge como una herramienta vanguardista con resultados
prometedores en otras aplicaciones experimentales, lo que llevó a la realización de éste
proyecto.
Un estudio cuantitativo realizado sobre una muestra representativa de la población
mexicana, en el cual se determinó características psicográficas y patrones de consumo, se
2
llevado a cabo con la finalidad de segmentar dicha población y definir el grupo más propenso
a comprar los productos de pastas de dientes de la empresa. Los atributos más influyentes de
la segmentación serían luego utilizados como señales de entrada para la creación de un modelo
de Support Vector Machines que reconociese a que grupo pertenece cada individuo.
La importancia de la identificación inicial del grupo mencionado, y sus consecuentes
reconocimientos con fines de investigación de mercado, radica en que la cantidad de dinero
que suele invertirse en mercadeo, cuya cifra puede llegar a ser 30% de los ingresos de la
compañía, puede ser optimizada de forma tal que, con mucha menos inversión se obtengan
mejores resultados. Además, la exploración de una aplicación sin precedentes aparentes para
Support Vector Machines, utilizando valores reales de consumo y características psicográficas,
constituye un importante valor agregado para el proyecto.
En los próximos capítulos se describen los detalles de la realización de éste proyecto,
iniciando con la descripción de la empresa donde se desarrolló, seguida de los objetivos
establecidos, una compilación de los temas necesarios para la comprensión del mismo, la
metodología empleada, una breve descripción del software utilizado, finalizando con la
exposición de los resultados obtenidos y las conclusiones correspondientes. Además, se
incluye una lista con las referencias bibliográficas citadas en este informe.
CAPÍTULO 2: DESCRIPCIÓN DE LA EMPRESA
En este capítulo presenta una breve descripción de la empresa donde fue desarrollado
este proyecto, incluyendo una reseña histórica, su propósito, valores y principios, así como su
estructura organizacional.
2.1 RESEÑA HISTÓRICA
Procter&Gamble fue fundada por William Procter y James Gamble el 12 de Abril de
1837 en Cincinatti, Ohio, Estados Unidos, al fusionar la fábrica de velas del primero junto con
la fábrica de jabones del segundo. Ambos fundadores crearon un esquema sencillo, lo cual
aseguró su fortalecimiento y crecimiento hasta lo que actualmente se conoce como P&G con
mas de 30 marcas registradas de jabones en el mundo. La buena calidad de sus productos hizo
que cada día su demanda fuera aumentando, lo cual comprobaba que el esquema de ventas
creado por el Sr. Procter, y el de fabricación creado por el Sr. Gamble, funcionaban.
Con esto fueron expandiéndose a otras regiones de Estados Unidos y en 1915 abrieron
su primera fábrica en Canadá, lo cual marca su apertura al mercado internacional.
Poco a poco fueron creciendo hasta llegar a conquistar el mercado Latinoamericano
abriendo las primeras subsidiarias ubicadas en Puerto Rico en 1947 y México en 1948. Para el
año de 1950, expande sus mercados a Francia, con lo cual marca su presencia en Europa. En el
mismo año, inicia operaciones en Venezuela, actuando como distribuidora de productos
importados. Dos años después, instala su primera planta en La Yaguara, Caracas para la
fabricación de Ace para luego, en 1954 incorporar a la línea de producción el jabón Camay.
En 1955 incorporó la crema dental Crest y posteriormente otros productos como Ariel, Drene
y Safeguard, los que pasaron a formar parte de la familia venezolana desde ese entonces hasta
la actualidad.
Para el año de 1980, la demanda de sus productos era tal que para poder cubrirla
tuvieron la necesidad de construir una segunda planta, la cual ubicaron en Barquisimeto, Edo.
4
Lara, donde luego, en los años 90, consolidan todas las actividades de producción de la
compañía en el territorio Venezolano.
En 1987, The Procter & Gamble Co. traslada a Caracas, Venezuela la gerencia de las
operaciones en Latinoamericanas, (Headquarter Latinoamericano), lo que significaría un
importante impulso a las actividades de la compañía en la Región, pues desde entonces, todas
las operaciones de la empresa con el mercado Latinoamericano se gerencian desde Venezuela.
Todo esto se vió respaldado por la inauguración de la nueva sede de P&G en Caracas, en el
edificio Sorokaima, en 1997, y con la incorporación del R&D (Centro de Desarrollo del
Producto Latinoamericano). En la actual sede, además del funcionamiento del R&D, también
funcionan unidades globales de negocio y la Organización de Desarrollo del Mercado (MDO).
Cabe destacar que en el mismo año se llevó a cabo la apertura del depósito de Barquisimeto,
con 10 mil metros cuadrados de planta y los sistemas más modernos para el manejo de
inventarios de productos terminados.
En Octubre de 1988 se asocia a Industrias Mammi, la cual era una empresa nacional
que para ese momento era la líder en lo que respecta a pañales y toallas sanitarias. La
adquisición total llegaría dos años más tarde.
En Enero del 2002, adquiere la industria Clairol, (tanto planta como centro de
distribución ubicado en Cagua), con lo cual adquiere la línea de productos y tintes para el
cabello conformado por Herbal Essences, Final Net , Infussium 23, Miss Clairol y MUM. Con
esto P&G de Venezuela terminaría por configurar lo que actualmente conforma su estructura
de almacenaje y distribución.
En Venezuela, Procter & Gamble desde sus inicios comercializa productos que han
llegado a formar parte de la vida diaria de los hogares venezolanos, los cuales incluyen
reconocidas marcas como Pantene, Pert Plus, Head&Shoulders, Herbal Essences, Ariel, Ace,
Rindex, Old Spice, Camay, Safeguard, Monclear, Secret, Pampers, Tess, Always, MUM,
Vicks, entre muchas otras.
5
2.2 PROPÓSITO
El propósito fundamental de la empresa es ofrecer productos de calidad y valor
superiores que mejoren la vida de los consumidores del mundo entero, por lo cual esperan
como resultado ser recompensados por los consumidores con liderazgo en ventas y
crecimiento de utilidades, permitiendo a su gente, sus accionistas y las comunidades en las
cuales viven y trabajan prosperen [P&G, 2005].
2.3 VALORES Y PRINCIPIOS
El principal valor de Procter & Gamble a lo largo de toda su historia ha sido su gente,
alrededor del cual giran todos los demás. La actitud del recurso humano de la compañía debe
orientarse por una serie de valores, que se relacionan entre sí y que confluyen en un personal
valioso, tal como lo representa la Figura 2.1. Los mismos incluyen liderazgo, integridad,
confianza, sentido de propiedad de la empresa, y pasión por el éxito.
LIDERAZGO
GENTE
PROPIEDAD
PASIÓN
POR
GANAR
INTEGRIDAD
CONFIANZA
Figura 2.1 Valores de Procter & Gamble
Fuente: [P&G, 2005]
Los principios fundamentales de la compañía y del personal que labora en ella son:
•
Demostrar respeto por todos los individuos.
•
Los intereses de la compañía y los del individuo son inseparables.
•
Tener un enfoque estratégico en el trabajo.
•
La innovación es la piedra angular del éxito.
6
•
Estar enfocados hacia el exterior de la empresa.
•
Valorar la maestría personal.
•
Buscar ser los mejores.
•
La interdependencia mutua como forma de vida.
[P&G, 2005]
2.4 ESTRUCTURA ORGANIZACIONAL
La Empresa posee una estructura organizacional dividida en cuatro pilares principales:
•
Unidades Globales de Negocio (Global Business Units—GBUs): Estas estructuras
centran su atención en el producto, al desarrollo de marcas. Deben garantizar su éxito
en el mercado a través del conocimiento del cliente, sus necesidades, sus quejas,
preferencias, etc; valiéndose a la vez políticas adecuadas de precios, control de costos,
garantía de calidad y suministro, etc.
Esta estructura, conformada por equipos
multidisciplinarios, vela por el crecimiento de las marcas basándose en la innovación;
pero no trabajan solos, siempre necesitan de la colaboración de otras áreas de la
organización para poder lograr un trabajo excelente. Existen cinco unidades de negocio
principales: Cuidado del Bebé, Femenino y de la Familia, Cuidado de la Belleza,
Cuidado del Hogar, Cuidado de la Salud y Comidas y Bebidas.
•
Organizaciones de Desarrollo del Mercado (Marketing Development Organization—
MDO): Su objetivo es garantizar la competitividad de la empresa en cada uno de los
mercados en los que esta participa. Para poder alcanzar los objetivos planteados, no
solo es necesario que la empresa cree relaciones con instituciones y con el entorno, si
no que también haga el reclutamiento y la capacitación del personal más calificado y
con las destrezas necesarias para así poder impulsar el desarrollo regional de la
compañía. Las Organizaciones de Desarrollo del Mercado responden a un criterio
geográfico siendo ocho en su totalidad: Norte América, Asia/ India/ Australia, Japón/
Corea, China, Europa Occidental, Oriente Medio/ África, Europa Central y Oriental, y
América Latina.
7
•
Servicios Globales de Negocio (Global Business Services—GBS): Proporcionan a
toda la organización una serie de procesos y servicios compartidos por toda la
Compañía haciendo uso de las economías de escala para garantizar calidad, costos y
rapidez de los recursos solicitados. Entre estas actividades destacan contabilidad y
tecnología de información.
•
Funciones Corporativas (Corporate Functions-CF): Su objetivo es garantizar que la
organización esté alineada en torno a su estrategia y a los objetivos que ha delimitado;
por lo tanto, está en su responsabilidad la divulgación de las normas y procedimientos,
así como velar por su cumplimiento.
[P&G, 2005]
En cada una de las unidades descritas trabajan grupos multifuncionales para lograr sus
objetivos. Estos grupos están liderizados por el departamento de Mercadeo, el cual se apoya en
Finanzas, Investigación de Mercado, Suministro de Productos, Ventas, Tecnologías de
Información, Desarrollo de Productos y Legal para crecer el negocio.
CAPÍTULO 3: OBJETIVOS
Este capítulo expone los objetivos generales y específicos que enmarcan al proyecto.
3.1 OBJETIVOS GENERALES
Explorar el potencial de Support Vector Machines como herramienta en la
identificación de segmentos de la población basados en patrones de consumo y características
psicográficas, con el fin de maximizar las ganancias de la empresa al diseñar productos e
implementar políticas de mercadeo dirigidos a los mismos.
3.2 OBJETIVOS ESPECÍFICOS
•
Estudiar las técnicas ampliamente utilizadas en Minería de Datos
•
Estudiar las bases teóricas detrás de Support Vector Machines
•
Investigar aplicaciones de Support Vector Machines
•
Conocer, describir y caracterizar las bases de datos disponibles y sus orígenes
•
Identificar e implementar las herramientas de Minería de Datos óptimas para la
segmentación y reducción de los datos
•
Generar distintos modelos de clasificación basados en Support Vector
Machines
•
Evaluar el desempeño de los modelos de clasificación creados
CAPÍTULO 4: MARCO TEÓRICO
El presente capítulo enmarca la información necesaria para la comprensión de los
temas, términos y métodos empleados en la ejecución del proyecto. Incluye una introducción a
las Máquinas de Aprendizaje como rama de la Inteligencia Artificial, seguido de una
descripción de los métodos de Minería de Datos utilizados, finalizando con el desarrollo
teórico, características y aplicaciones de Support Vector Machines. Por último, concluye con
un acercamiento al Mercadeo y a la Investigación de Mercados dada su importancia en el
contexto del proyecto.
4.1 MÁQUINAS DE APRENDIZAJE
Durante las últimas dos décadas, la acelerada evolución de la capacidad de
procesamiento de las computadoras ha traído consigo un sinfín de aplicaciones nuevas,
haciendo posible el desarrollo de teorías que, con las herramientas informáticas de la época,
eran imposibles de implementar.
Entre estas aplicaciones se encuentra el Aprendizaje
Automático que, de la misma forma en que los zoólogos y sociólogos estudian el aprendizaje
en animales y el hombre, estudia el aprendizaje en las máquinas.
El Aprendizaje Automático surge como una rama de la Inteligencia Artificial (IA) que,
uniendo fundamentos y herramientas de áreas del conocimiento tan disímiles como las que se
enumeran a continuación, busca desarrollar técnicas que permitan a las máquinas aprender:
•
Psicología: no se pueden separar los términos inteligencia y aprendizaje-
adaptación.
•
Biología: la adaptación, en todas sus vertientes, no se puede separar de nosotros
•
Artes: permite nuevas formas de creación.
•
Matemáticas: estadística e inducción son dos formas clásicas de análisis de
datos y generalización.
•
Ingeniería: realimentación.
10
•
Informática: Inteligencia Artificial como generadora de nuevas soluciones.
[NRL, 2005]
El Aprendizaje Automático generalmente provoca cambios en los sistemas que
realizan tareas asociadas con IA (ver Figura 4.1), al integrar los métodos y técnicas para lograr
juicio en tareas como reconocimiento, planificación, clasificación y predicción. “A partir de
un conjunto de datos, se realiza el proceso de aprendizaje automático el cual adquiere el
conocimiento que luego puede expresar” [Aguilar, 2002].
Figura 4.1 Un sistema de Inteligencia Artificial
Fuente: [Aguilar, 2002]
La construcción de máquinas capaces de aprender a través de experiencias pasadas, ha
sido un tema de debate desde hace mucho tiempo por el escepticismo de muchos. La
importancia estratégica de estos modelos radica en que actualmente los algoritmos clásicos de
programación, presentes en los modelos matemáticos, no son capaces de resolver múltiples
tareas. Muestra de esto son los caracteres escritos a mano, de los cuales hay innumerables
ejemplos, pero no existe un algoritmo programable capaz de reconocerlos [Cristianini y
Shawe-Taylor, 2000]. De esta forma, las Máquinas de Aprendizaje intentan simular el modo
de aprendizaje del ser humano; un niño al ser expuesto a distintos tipos de automóviles, con el
entrenamiento de sus padres u otro agente que le enseña a qué grupo pertenecen,
11
eventualmente será capaz de diferenciar correctamente un carro deportivo que jamás ha visto,
asociando sus características (posiblemente inarticulables) con experiencias pasadas.
A la técnica de usar ejemplos en el entrenamiento de una máquina para la obtención de
un programa que resuelva un problema planteado, se le conoce como “metodología del
aprendizaje”. Ésta contempla dos tipos:
•
Aprendizaje supervisado: el algoritmo produce una función que establece una
correspondencia entre las entradas y las salidas deseadas del sistema a partir de los
ejemplos proporcionados o data de entrenamiento.
•
Aprendizaje no supervisado: todo el proceso de modelado se lleva a cabo sobre un
conjunto de ejemplos constituido tan sólo por entradas al sistema. No se tiene información
sobre las categorías de esos ejemplos y el objetivo es entender mejor la data.
Otra forma de dividir los métodos de aprendizaje es de acuerdo a la forma en que la
data de entrenamiento es proporcionada: si toda la data es suministrada al inicio del
aprendizaje, se conoce como aprendizaje en lote. Si se proporciona un ejemplo a la vez, dando
una salida estimada a la entrada antes de recibir la salida verdadera, actualizando el modelo
con cada ejemplo, se denomina aprendizaje en línea.
En los primeros intentos de Máquinas de Aprendizaje, el objetivo era lograr modelar
una función conocida a través del entrenamiento aplicado, por lo que su eficiencia se medía en
qué tan buena era la función obtenida por la máquina. En la actualidad, las aplicaciones para
las cuales se intentan emplear dichas máquinas son mucho más complicadas: además de no
conocer de antemano la función que relaciona a las entradas y salidas de los ejemplos, estos
últimos pueden tener ruido inherente. Gracias a esto, el nuevo objetivo se centra en clasificar
de forma correcta data que no era parte de los ejemplos empleados en el entrenamiento, lo cual
es conocido como generalización.
La obtención de un buen desempeño de la generalización de una Máquina de
Aprendizaje, a partir de un número finito de ejemplos, depende de un buen balance entre la
capacidad de la máquina (habilidad de aprender de la data de entrenamiento sin ningún error)
y la exactitud de la data de entrenamiento [Burgues, 1998]. En este sentido, una máquina con
12
mucha capacidad es, como en el caso de los automóviles deportivos, aquel niño que tiene
memoria fotográfica y al presentarle un deportivo con número de placa distinto a los que se le
mostró en el entrenamiento, lo declara no deportivo; mientras que una máquina con poca
capacidad es como el niño despistado que declara cualquier cosa que tenga neumáticos como
deportivo.
Una de las características que hacen sumamente atractiva a la metodología del
aprendizaje, consiste en su gran cantidad de aplicaciones: éstas van desde un mejor
entendimiento del comportamiento humano, lo cual inspiró los primeros trabajos en redes
neuronales, hasta la posibilidad de evitar engorrosos procesos de diseño y programación de
soluciones para los problemas tradicionales, con el simple entrenamiento a través de ejemplos
etiquetados. [Cristianini y Shawe-Taylor, 2000]
El concepto detrás de la metodología del aprendizaje es bastante asimilable y
entendible dentro del paradigma del aprendizaje humano, pero esto no debe disfrazar la
complejidad del tema a la hora de llevarlo a la práctica. Al final todo se resume en las
matemáticas (las computadoras sólo entienden números), las cuales han proporcionado
grandes avances en las técnicas empleadas. Sin embargo, asuntos como la selección del tipo de
función a través de la cual se efectúa el mapeo de las entradas a las salidas proporcionadas y
otros parámetros de ajuste, son hasta ahora resueltas por ensayo y error para cada aplicación
especifica.
4.2 MINERÍA DE DATOS
Con el advenimiento de los avances tecnológicos, la información se ha convertido en
una herramienta muy valiosa. No obstante, la capacidad para recolectar y almacenar grandes
cantidades de datos ha generado la necesidad de técnicas y procesos para la optimización de su
uso. Lo anterior es conocido como el proceso de descubrimiento de conocimiento, e incluye
las siguientes etapas:
•
Determinación de objetivos
•
Preparación de datos
•
Transformación de datos
13
•
Minería de Datos
•
Análisis de resultados
•
Asimilación del conocimiento
La Minería de Datos surge como parte del proceso de descubrimiento de conocimiento,
buscando predecir y describir procesos a través de la síntesis y análisis de datos. Puede
considerarse el núcleo fundamental de la ingeniería del conocimiento, constituyendo el
“proceso de exploración y análisis de grandes cantidades de datos de forma automática o
semiautomática para descubrir patrones y reglas y poder utilizarlos en la toma de decisiones”
[Aguilar, 2002].
4.2.1 Técnicas
En el desarrollo de Máquinas de Aprendizaje, el manejo de grandes cantidades de
información se torna una necesidad, siendo la Minería de Datos quien proporciona técnicas de
tratamiento de información para aprendizaje supervisado (predicción, estimación y
clasificación) y no supervisado (agrupamiento y análisis de asociación) que se describen a
continuación:
•
Clasificación: consiste en designar un elemento a una clase predefinida, de
acuerdo a ciertas características proporcionadas. Generalmente los datos se separan
en atributos que representan características, donde la clase suele estar como un
atributo adicional en la data de entrenamiento.
•
Estimación: determina el valor de una variable continua, de acuerdo a los valores
de las entradas. Se basa en la clasificación añadiendo la base probabilística.
•
Predicción: puede ser considerado estimación o clasificación según sea el caso,
pero la diferencia radica en el énfasis sobre el tipo de resultado obtenido, el cual, al
proporcionar un valor futuro, no se puede verificar hasta que los hechos ocurran.
•
Agrupamiento: consiste en segmentar un conjunto de datos en grupos con
características similares que, a diferencia de la clasificación, no son conocidos
previamente.
14
•
Análisis de asociación: determina las relaciones que existen entre los elementos
de un conjunto de acuerdo a sus características.
A continuación se dará una explicación más detallada sobre Agrupamiento y
Componentes Principales, formando este último parte de los análisis de asociación. La
clasificación será discutida más adelante dentro del marco de Support Vector Machines.
4.2.1.1 Agrupamiento
El Agrupamiento es una técnica de análisis exploratorio de datos que busca definir
grupos con características similares. La misma sugiere varios resultados, que deben ser
verificados y afinados de forma tal que tengan sentido dentro del contexto en el que se
enmarcan los datos.
Los grupos son definidos bajo el criterio de distancia entre los datos. De esta forma,
aquellos que se encuentren distanciados pertenecerán a grupos distintos, mientras que si ocurre
lo contrario serán etiquetados dentro del mismo grupo.
Existen básicamente dos tipos de Agrupamiento: jerárquico y no jerárquico. En el
primero las características que hayan resultado en un grupo deben permanecer juntas; no
siendo así en el segundo.
Dentro del Agrupamiento jerárquico existen varias formas de medir la distancia entre
los datos (ver Figura 4.2). A continuación se numeran los más empleados:
•
Vecino más próximo: calcula la distancia entre dos grupos como la menor
distancia entre todos los pares de puntos de cada grupo.
•
Vecino más lejano: calcula la distancia entre dos grupos como la mayor entre
todos los pares de puntos de cada grupo.
•
Centroide: calcula la distancia entre dos grupos como la distancia entre los
promedios de puntos de cada grupo.
•
Promedio de relación entre grupos: calcula la distancia entre dos grupos como el
promedio de las distancias entre todos los pares de puntos de cada grupo.
15
a. Vecino más próximo
b. Vecino más lejano
c. Centroide
d. Promedio de relación entre grupos
Figura 4.2 Métodos de medición de distancia entre datos
Fuente: [SPSS, 2002]
El Agrupamiento jerárquico proporciona como resultado una especie de árbol
genealógico de grupos, en el cual cada grupo se subdivide en un mayor número de
conglomerados de menor tamaño. La representación gráfica de lo anterior se denomina
dendrograma, el cual incluye las distancias entre las subdivisiones, así como el número de
casos resultantes en cada subgrupo (ver Figura 4.3).
16
Figura 4.3 Ejemplo de Dendograma
Fuente: [SPSS, 2002]
El Agrupamiento no jerárquico se emplea cuando se tiene un conocimiento previo de
los datos que permitan estimar el número de grupos en que se divide la data, ya que debe ser
proporcionado al inicio del análisis. Su método más comúnmente empleado es el algoritmo de
agrupamiento K-medias, el cual basa sus mediciones de distancias en el centroide descrito
anteriormente.
El lector interesado en profundizar sobre Agrupamiento, ver [Politécnico de Milano,
2005].
4.2.1.2 Componentes Principales
El método de tratamiento de los datos conocido como Componentes Principales se
utiliza generalmente con el fin de reducir el número de parámetros o características empleadas
para tomar decisiones. En muchas aplicaciones se utilizan variables que están altamente
correlacionadas entre si, o poco correlacionadas con una variable dependiente de interés. Al
17
realizar un estudio de componentes principales, se discriminan características innecesarias o
redundantes de forma para simplificar el modelo.
Una componente principal es una combinación lineal de variables observadas,
independiente (ortogonal) de otras componentes. La primera componente principal considera
la mayor cantidad de varianza en la data de entrada; la segunda componente considera la
mayor cantidad de varianza restante en la data, y así sucesivamente. Cabe acotar que el hecho
de que sean componentes ortogonales implica que no están correlacionadas, lo que facilita la
interpretación.
El lector interesado en profundizar sobre Componentes Principales, ver [Smith, 2002].
4.3 SUPPORT VECTOR MACHINES
Support Vector Machines es una nueva generación de sistemas de aprendizaje,
producto de grandes avances en la teoría de aprendizaje estadístico en las últimas dos décadas,
desarrollado principalmente por Vapnik y sus colaboradores. Desde sus orígenes a principios
de los años noventa, han probado ser muy útiles en la solución de problemas del mundo real,
tales como reconocimiento de escritura a mano, clasificación de imágenes, análisis de
secuencias de ADN, etc. Es por ello que hoy en día es considerada una herramienta con
inmenso potencial en las áreas de Máquinas de Aprendizaje y Minería de Datos, tanto para
clasificación como para regresión.
A continuación se describen las características que forman Support Vector Machines,
haciendo énfasis en su aplicación como clasificador. Se inicia con un estudio más profundo de
clasificadores lineales, seguido de la introducción a los dominios característicos (feature
spaces) y su relación con los Kernels, la Teoría de Generalización y la Teoría de
Optimización, finalizando con sus aplicaciones en Clasificadores Support Vector.
4.3.1 Clasificadores Lineales
En aprendizaje supervisado, como se explicó anteriormente, se le proporciona a la
máquina de aprendizaje un grupo de ejemplos (entradas) con sus correspondientes etiquetas o
grupo al que pertenecen (salidas). Luego de tener estos vectores de entradas y salidas, se
18
puede elegir una serie de hipótesis referente al tipo de clasificador que puede separarlos de
forma óptima. Debido a su simpleza, los clasificadores lineales son utilizados como base para
otros más complejos, siendo el caso de la clasificación binaria su forma elemental.
La clasificación binaria se lleva a cabo generalmente con una función real
, siendo la entrada x=(x1, …,xn)´ asignada a la clase positiva si f ( x) ≥ 0 y a la
f:
negativa en caso contrario. La función f (x) es una función lineal de x ∈ X , que puede ser
escrita como:
f ( x) = w ⋅ x + b
n
= ∑ wi xi + b ,
i =1
donde w y b ∈
son los parámetros de control vector de peso y polarización
respectivamente, determinados a través del los datos de entrenamiento. La función de decisión
es signo( f (x) ), donde por convención signo(0) = 1. La representación gráfica de lo anterior
se muestra en la Figura 4.4, en donde un hiperplano separa a dos clases de datos.
Figura 4.4 Hiperplano (w, b) separando una data de entrenamiento bidimensional
Fuente: [Cristianini y Shawe-Taylor, 2000]
19
Desde hace más de cuatro décadas, existen muchos algoritmos para la separación de
dos clases de datos por medio de un hiperplano. Los más conocidos son el Perceptrón de
Rosenblatt y Mínimos Cuadrados, a través de los cuales se minimiza una denominada función
de costo para hallar una solución. El problema del primero radica en que, dependiendo del
orden de los datos de entrenamiento, el resultado puede variar no asegurando de esta manera
una solución óptima.
El algoritmo de Mínimos Cuadrados se encarga de minimizar la siguiente función de
costo denominada función cuadrática de pérdida:
l
L( w, b) = ∑ ( yi − w ⋅ xi − b) 2 .
i =1
Al obtener los valores del vector de peso y la polarización que minimicen la función
cuadrática de costo, se consigue el hiperplano con el máximo margen, el cual se define para un
punto específico como la distancia mínima de dicho punto al hiperplano de decisión (ver
Figura 4.5). Dicho margen máximo se conoce como el margen del conjunto de entrenamiento,
y se muestra en la Figura 4.6.
Figura 4.5 Márgenes para dos puntos para un hiperplano
Fuente: [Cristianini y Shawe-Taylor, 2000]
20
Figura 4.6 Margen del conjunto de entrenamiento
Fuente: [Cristianini y Shawe-Taylor, 2000]
Otro concepto importante es el de margen estacionario, definido para un punto
ejemplo como la distancia por la cual dicho punto fracasa en tener un margen determinado.
Esto es, para un punto que se encuentra ubicado del lado opuesto a su clase (por ende
clasificado erróneamente por el hiperplano), la distancia que lo separa de cierto margen,
pudiéndose observar geométricamente en la Figura 4.7.
Figura 4.7 Margen estacionario de dos puntos
Fuente: [Cristianini y Shawe-Taylor, 2000]
21
Una importante propiedad de los clasificadores lineales, explotada ampliamente por
Support Vector Machines, es su forma dual. Esta es el resultado de reescribir la función de
decisión como sigue:
h( x) = sgn ( w ⋅ x + b )
⎛
= sgn ⎜⎜
⎝
l
⎞
i =1
⎠
∑α i yi xi ⋅ x + b ⎟⎟
⎛ l
⎞
= sgn ⎜ ∑ α i yi xi ⋅ x + b ⎟ .
⎝ i =1
⎠
Para esto, se parte de la suposición de que
l
w = ∑ α i y i xi .
i =1
Lo anterior resulta de asumir que el vector de peso al inicio del algoritmo es el vector
cero, por lo que la hipótesis final será una combinación lineal de los puntos de entrenamiento
dada por el vector α . Sus beneficios serán evidentes en la siguiente sección, cuando se
introduzca el concepto de Kernel.
Para el caso de clasificación multi-clase, cuyo dominio de salida es Y = {1, 2, …, m},
es asignado un vector de peso y una polarización para cada una de las m clases, siendo la
función de decisión
c( x) = max( wi ⋅ x + bi ) .
1≤i ≤ m
Lo anterior equivale geométricamente a asociar un hiperplano a cada clase, y asignar
un punto nuevo x a la clase que tenga el hiperplano más lejano.
22
4.3.2 Dominios característicos y Kernels
En general, los problemas de la vida real son mucho más complejos para ser
solucionados con funciones lineales: la solución debería ser una combinación lineal de sus
atributos, cosa que rara vez ocurre. Además, la forma en que los datos son presentados a la
máquina de aprendizaje determina la complejidad de la función de decisión óptima buscada, lo
cual determina a su vez la dificultad del aprendizaje.
Los dominios o espacios característicos pueden definirse como la representación de los
datos en una forma más simple para el aprendizaje por parte de la máquina. Esto se logra al
trasladar las variables o atributos de un dominio X,
a un nuevo dominio F (dominio
característico) a través de una transformación de la forma:
x = ( x1 ,..., xn ) a φ ( x ) = (φ1 ( x ),..., φ N ( x )) ,
donde F = Φ( x) | x ∈ X. Para una mejor ilustración, puede verse la Figura 4.8, en donde antes
de la transformación los datos no eran separables por un clasificador lineal, pero luego si.
Figura 4.8 Ejemplo del uso de dominios característicos
Fuente: [Cristianini y Shawe-Taylor, 2000]
Aunque existen distintas opiniones en cuanto a los pasos a seguir para la creación del
espacio característico, esto dependerá básicamente de los datos, pudiendo llegar a convertirse
en un proceso iterativo.
23
Un primer paso, sugerido en [Cristianini y Shawe-Taylor, 2000], puede ser la reducción
de dimensionalidad, que consiste básicamente en identificar la menor cantidad de
características que sigan conteniendo la información esencial de los atributos originales, de la
siguiente forma:
x = ( x1 ,..., x n ) a φ ( x ) = (φ1 ( x ),..., φ d ( x )), d < n .
La reducción de dimensionalidad, además de simplificar los datos reduciendo la
complejidad computacional, permite mejorar la generalización de la máquina de aprendizaje,
ya que empeora al aumentar el número de características (maldición de dimensionalidad).
Otro paso para la creación de un espacio característico óptimo puede incluir la detección
de características irrelevantes y su eliminación; el análisis de componentes principales, al
determinar la varianza de cada característica y por ende su influencia sobre los resultados,
permite no sólo eliminar aquellas que aparentemente no son relevantes, sino que “proporciona
una transformación de los datos a un espacio característico en el cual las nuevas
características son funciones lineales de los atributos originales y están ordenados por la
cantidad de varianza que los datos muestran en cada dirección” [Cristianini y Shawe-Taylor,
2000]. De esta forma, el análisis de componentes principales además de ayudar en la detección
y eliminación de características irrelevantes, puede reducir la dimensionalidad creando un
espacio característico.
Una vez obtenido el dominio característico, la función de decisión resultante y su
representación dual son de la forma:
N
N
i =1
i =1
f ( x ) = ∑ wiφi ( x ) + b =∑ α i yi φ ( xi ) ⋅ φ ( x ) + b .
Debido a que la representación dual permite calcular el producto interno
< Φ ( x i ) ⋅ Φ ( x) > como función de los atributos originales, se puede construir una máquina de
aprendizaje no lineal en un sólo paso, utilizando un clasificador lineal con un espacio
24
característico K que haga, tanto la transformación no lineal, como el producto interno de la
forma:
K ( x, z ) = φ ( x ) ⋅ φ ( z )
,
donde x, z ∈ X y la función K es denominada Kernel. Al usar la representación dual, la
dimensión del dominio característico no influye en la intensidad del cálculo computacional;
esto es por que no se representan los vectores característicos de forma explícita sino a través
del producto interno. De esta forma, el número de operaciones es limitado por el tamaño del
conjunto de entrenamiento, sin influir la asunción sobre el valor inicial del vector de peso
descrita en la sección anterior.
Existen varios enfoques en cuanto al uso de Kernels; al abordar el problema buscando
un Kernel que contenga de forma implícita la transformación de los datos al dominio
característico, se evita la búsqueda de dicha función, mientras que al analizar los datos de
forma intensiva se puede obtener un Kernel más apropiado al crear una transformación
óptima. El primer acercamiento se emplea generalmente cuando se posee experiencia sobre el
tipo de datos, pero se debe comprobar la validez del la transformación implícita al satisfacer
ciertas condiciones dadas por el teorema de Mercer detallado en [Cristianini y Shawe-Taylor,
2000].
Se pueden mencionar tres Kernels reconocidos por ser muy efectivos en aplicaciones
diversas:
• Kernel Lineal:
K (xi , x j ) = xiT x j
• Kernel Polinomial:
(
)
K (xi , x j ) = xiT x j + 1
d
25
• Kernel RBF (Radial Basis Function):
K (x i , x j ) = e
−
xi x j
2
σ2
Los Lineal y Polinomial son los más básicos y generales, empleados usualmente
cuando los datos de cada grupo están muy concentrados alrededor de cierto valor. El RBF por
su parte “es por mucho la alternativa más popular de tipos de Kernels usados en Support
Vector Machines” [Sutton y Barto, 1998]; esto se debe principalmente por su excelente
desempeño en todo el rango de los números reales, aplicando separación de gaussianas con
parámetro de dispersión
σ (ver Figura 4.9). Cabe acotar que este último presenta resultados
opuestos cuando se trata de datos de valores no continuos.
Figura 4.9 Ejemplo de RBF unidimensional
Fuente: [Sutton y Barto, 1998]
4.3.3 Teoría de Generalización
La importancia de la generalización de una máquina de aprendizaje fue expuesta en
secciones anteriores, pero la introducción de los Kernels hace aún más importante su control.
Esto se debe a que con la libertad en cuanto al número de dimensiones proporcionado por los
Kernels, se puede tender a ser demasiado específico en cuanto a las características
(overfitting), que es lo contrario al concepto de generalización.
Las investigaciones de Vapnik y Chervonenkis han arrojado varios límites
matemáticos sobre la generalización de clasificadores lineales, los cuales indican cómo
controlar la complejidad de las soluciones, siendo ésta la base de Support Vector Machines. Su
26
Teorema principal indica que, con probabilidad 1- δ , cualquier hipótesis h ∈ H que es
consistente con los datos de entrenamiento presenta un error
2⎛
2el
2⎞
+ log ⎟ ,
err (h ) ≤ ε (l, H , δ ) = ⎜ d ⋅ log
d
δ⎠
l⎝
siendo H un dominio de hipótesis de soluciones con dimensión VC d para l ejemplos
aleatorios, siempre y cuando d ≤ l y l > 2 / ε .
La dimensión VC es una medida de la capacidad de la máquina y “para un grupo de
funciones { f (α )} se define como el número máximo de puntos de entrenamiento que pueden
ser quebrantados por { f (α )} ” [Burges, 1998], entendiéndose por quebrantar el hecho de
separar mediante hiperplanos cierto número de puntos de todas las formas posibles. Un
ejemplo de esto se observa en la Figura 4.10 para el caso de R 2 . En general, la dimensión VC
de un grupo de hiperplanos orientados en R n es n + 1.
Figura 4.10 Tres puntos en R quebrantados por líneas orientadas
2
Fuente: [Burgues, 1998]
Otros límites importantes se relacionan con los márgenes definidos en secciones
anteriores, y son derivados del Teorema de Vapnik- Chervonenkis. El primero se conoce como
27
el Limite de Margen Máximo según el cual, con probabilidad 1- δ , cierta hipótesis f ∈ L con
margen mayor o igual que γ , presenta un error
2 ⎛ 64 R 2
elγ
128lR 2
4⎞
⎟
err ( f ) ≤ ε (l, L , δ , γ ) = ⎜⎜ 2 log
log
log
+
l⎝ γ
4R
γ2
δ ⎟⎠ ,
siendo L un dominio de funciones lineales reales, l el número de ejemplos aleatorios y R la
distancia radial que encierra a todos los puntos, siempre y cuando 64 R 2 / γ 2 < l y l > 2 / ε .
El segundo es el Límite de Margen Flexible según el cual, bajo los mismos parámetros
del límite anterior, y con margen estacionario ξ , existe un parámetro c tal que el error de la
hipótesis f es
2
c ⎛⎜ R + ξ
err ( f ) ≤
l⎜ γ2
⎝
2
1 ⎞⎟
log l + log
δ ⎟⎠ .
2
La importancia del Límite de Margen Máximo radica en su independencia de la
dimensión de los datos de entrada, pero a su vez necesita que los datos sean separables con
cierto margen γ . En los casos de la vida real, los datos generalmente contienen ruido que
puede hacer que no sean completamente separables, caso en el que este límite no proporciona
ninguna información.
Para solventar el problema del caso no separable, surge el Límite de Margen Flexible,
el cual toma en cuenta la cantidad por la que los puntos fallan en tener cierto margen γ . Este
límite sugiere minimizar dicha cantidad para optimizar el desempeño de la máquina, lo cual no
necesariamente implica minimizar el número de clasificaciones incorrectas, que implicaría un
mayor esfuerzo computacional.
28
4.3.4 Teoría de Optimización
Luego de presentar la Teoría de Generalización, es claro que el problema de
aprendizaje de la máquina se ha convertido en un problema de minimización de funciones de
costo, sujetas a ciertos límites. La Teoría de Optimización es la rama de las matemáticas que
se encarga de caracterizar las soluciones a este tipo de problemas, desarrollando algoritmos
efectivos para hallarlas.
Para entrenar un Support Vector Machine, el problema planteado se limita a la
solución de funciones cuadráticas y convexas, siendo estas últimas aquellas que poseen un
solo mínimo local (por ende es mínimo global). El método empleado para la minimización de
este tipo de funciones es el de los multiplicadores de Lagrange, que, para la optimización de
una función f (w) con restricciones hi(w) = 0, utiliza el Lagrangiano:
m
L(w, β ) = f (w) + ∑ β i hi (w) ,
i =1
donde los coeficientes βi se llaman multiplicadores de Lagrange. El Teorema de Lagrange
especifica que para obtener el mínimo de la función f (w), se deben cumplir las siguientes
condiciones:
∂L(w, β )
=0
∂w
∂L(w, β )
=0.
∂β
Luego, al generalizar en cuanto a las restricciones impuestas sobre w añadiendo
gi(w) ≤ 0, se obtiene el Lagrangiano generalizado:
k
m
i =1
i =1
L(w,α , β ) = f (w) + ∑ α i g i (w) + ∑ β i hi (w)
29
= f (w) + α ' g (w) + β ' h(w) .
El Teorema de Kuhn-Tucker expone que dado el Lagrangiano generalizado, la
optimización se consigue al obtener α * , β * tales que
∂L(w,α , β )
=0,
∂w
∂L(w,α , β )
=0,
∂β
α i g i (w) = 0 , i = 1,..., k ,
g i (w) ≤ 0 , i = 1,..., k ,
α i ≥ 0 , i = 1,..., k .
La última relación es conocida como la condición complementaria de Karush-KuhnTucker, e implica que sólo cierto número de variables de los datos de entrenamiento tendrán
valores de α no nulos. Dichos puntos son denominados vectores de soporte, ya que son los
que determinan la función de decisión, siendo la razón del nombre Support Vector Machines.
4.3.5 Clasificadores Support Vector
Las secciones anteriores describen cómo controlando la capacidad de la máquina con
base en la Teoría de Generalización y empleando las técnicas matemáticas descritas en la
Teoría de Optimización, un clasificador Support Vector “aprende” hiperplanos óptimos,
aprovechando las ventajas del uso de Kernels con dominio característico implícito.
Dependiendo del límite utilizado en la Teoría de Generalización, existen varios
clasificadores Support Vector. Los dos más importantes son el Clasificador de Margen
30
Máximo por razones históricas, y el Clasificador de Margen Flexible, cuyos límites empleados
fueron descritos en la sección 4.3.3 (Limite de Margen Máximo y Limite de Margen Flexible,
respectivamente). Debido a las características de dichos límites, el primero sólo funciona en
datos separables, mientras que el segundo procura una mejor generalización, permitiendo la
clasificación incorrecta de ciertos datos de entrenamiento como se muestra en el ejemplo de la
Figura 4.11.
a. Clasificador de Margen Máximo
b. Clasificador de Margen Flexible
Figura 4.11 Ejemplo de Clasificadores Support Vector para cierta data de entrenamiento
Fuente: [Cristianini y Shawe-Taylor, 2000]
Existen varios métodos para estimar los errores en los clasificadores, pero los
ampliamente aceptados son los siguientes:
• Técnica “Holdout” (retener fuera): utiliza una porción del total de registros disponibles
como conjunto de entrenamiento, y el resto como conjunto de prueba, con el cual se
calcula el error de clasificación (ver Figura 4.12).
31
Figura 4.12 Estimación del error de clasificación con la técnica “Holdout”
Fuente: [Aguilar, 2002]
• Técnica de validación cruzada: el conjunto total de registros es dividido en k grupos
aleatorios mutuamente excluyentes, de aproximadamente el mismo tamaño. Luego se
realizan k entrenamientos, seleccionando un conjunto de prueba distinto, siendo el error
estimado la media de los k errores obtenidos (ver Figura 4.13).
Figura 4.13 Estimación del error de clasificación con la técnica de validación cruzada
Fuente: [Aguilar, 2002]
32
4.3.6 Aplicaciones de Support Vector Machines
El número de aplicaciones de esta herramienta crecen cada día, y como se expuso
anteriormente, las áreas en donde es utilizada son muy variadas. A continuación se presenta
parte de una lista disponible y detallada en [ClopiNet, 2005], que contabiliza algunas de las
aplicaciones dadas a Support Vector Machines por investigadores alrededor del mundo:
•
Clasificación de expresiones faciales
•
Clasificación de textura a través de imágenes
•
Aprendizaje en línea (e-learning)
•
Clasificación de texto
•
Agrupamiento de imágenes
•
Reconocimiento de voz
•
Teoría del caos
•
Predicción de velocidad de tráfico y tiempo de viaje
•
Estructura de proteínas
•
Identificación de exones alternativos en secuencias de ADN
•
Detección de intrusos en redes de computadoras
•
Efectos de la quimioterapia en probabilidades de sobrevivir al cáncer de mama
•
Identificación de Quarks y partículas en física energética avanzada
•
Reconocimiento de objetos 3-D
4.4 MERCADEO
El mercadeo se entiende por la actividad que lleva a cabo una compañía para vender los
productos/servicios que manufactura/presta, comprendiendo cuatro componentes principales:
• Productos y Servicios: establece una estrategia en cuanto al producto o servicio a
vender, la cual define el tipo del mismo (especializado, de alta calidad, versiones,
etc.).
33
• Promoción: define la estrategia de publicidad e interacción con los consumidores,
la cual debido a los elevados costos de espacios en medios de comunicación masivos,
deben ser optimizados para tener un buen retorno de inversión (ROI).
• Precio: establece la estrategia a tomar en cuanto al precio del producto, tomando en
cuenta que mayor precio implica menor volumen en ciertos casos, pero en otros se
traduce en el resultado opuesto (elasticidad negativa).
• Distribución: define en que tipo de locales y canales va a estar disponible el
producto, así como las zonas geográficas de los mismos.
Bajo una buena gerencia, las estrategias adoptadas en cada uno de los componentes
descritos están orientadas a convencer a los consumidores a probar o seguir usando un
producto específico. Para determinar la combinación óptima de los mismos se deben llevar a
cabo las siguientes tareas:
1. Segmentación de Mercado: “es la división del mercado en grupos homogéneos
de consumidores, cada uno de ellos reaccionando diferente ante promociones,
comunicación, precio y otras variables de las componentes del mercadeo” [Recklies,
2001a]. La idea de dirigir los esfuerzos para la venta de un producto a toda la
población es poco eficiente por sus elevados costos (bajo ROI); la segmentación se
encarga de diferenciar varios grupos de consumidores cuyas características tengan
sentido práctico a la hora de diferenciarlos entre sí. Dichas características
regularmente se refieren a geográficas (país o región, área metropolitana o rural),
demográficas (edad, sexo, estado civil, ingreso económico, religión, raza, educación,
ocupación), psicográficas (estatus social, estilo de vida) y de comportamiento
(intensidad de uso del producto, lealtad a cierta marca, lugar de compra).
2. Identificación de Mercados Blanco (targeting): luego de tener los grupos
diferenciados por la etapa anterior, se evalúa cuál o cuáles de ellos presenta
características más afines con el producto. “Es importante asegurar que el target
seleccionado genere suficiente volumen para obtener ganancias” [Bucherer y
Robinson, 2003].
3. Posicionamiento: finalmente se decide de qué forma se presentará el producto al
target elegido, atendiendo sus necesidades y expectativas. Se trata de “una imagen
34
para un producto en las mentes de los consumidores” [Recklies, 2001b], la cual
incluye precio, calidad, valor, y confiabilidad, entre otros, no necesariamente siendo
los reales. Es importante escoger una imagen que diferencie el producto de la
competencia, de forma tal que resulte atractivo para el consumidor. En la Figura 4.14
se muestra uno de los elementos más importantes del posicionamiento, que es la
relación entre precio percibido y calidad; mientras más arriba y a la izquierda de la
diagonal trazada por la mayoría de los productos, mejor posicionamiento se tiene.
Figura 4.14 Posicionamiento por calidad versus precio percibido
Fuente: [Recklies, 2001b]
Para lograr obtener buenos resultados en dichas tareas surge la Investigación de
Mercado, rama del mercadeo que se encarga entre muchas cosas de:
•
Entender el potencial del mercado (tamaño)
•
Analizar el comportamiento del mercado (tendencias)
•
Entendimiento de los consumidores
•
Definición de consumidor blanco (target)
•
Analizar a la competencia y sus participaciones en las ventas de la categoría de
interés
CAPÍTULO 5: MARCO METODOLÓGICO
Este capítulo describe la metodología utilizada para la realización del proyecto, la cual
incluye una revisión bibliográfica inicial, seguida de la etapa de desarrollo que abarca todos
los pasos de un proyecto de Minería de Datos.
5.1 REVISIÓN BIBLIOGRÁFICA
Debido a la complejidad teórica del proyecto y a su avanzado nivel, una investigación
bibliográfica exhaustiva fue requerida. Esta incluyó libros, publicaciones en medios
especializados (papers) y páginas web.
5.2 DESARROLLO DEL PROYECTO
A lo largo del la etapa de desarrollo del proyecto se siguió la metodología sugerida por
el modelo de referencia CRISP-DM, cuyas siglas significan Proceso Estándar para Minería de
Datos en Industrias Varias (Cross Industry Standard Process for Data Mining). Cabe acotar
que dicho modelo incluye muchas etapas del proceso de descubrimiento de conocimiento
discutido en el marco teórico.
Este modelo consiste en seis fases mostradas en la Figura 5.1 en las cuales, como
indican las flechas, se avanza o retrocede dependiendo de los resultados obtenidos en cada una
de ellas. La flecha exterior simboliza en ciclo natural de la Minería de Datos, no terminando el
mismo cuando una solución es obtenida, ya que ésta puede traer consigo nuevas y mejor
enfocadas interrogantes sobre el tema en el que se enmarcan.
36
Figura 5.1 Fases del modelo de referencia CRISP-DM
Fuente: [Chapman et al., 1999]
5.2.1 Entendimiento del negocio
La fase inicial se enfoca en entender los objetivos de negocio, los objetivos del
proyecto y los requisitos para lograrlo, para luego convertir este conocimiento en un problema
de Minería de Datos e incluye:
• Antecedentes: provee una visión del contexto del proyecto y contiene el área en
el que se desarrolla, problemas identificados y razones por las cuales la Minería de
Datos puede proveer una solución.
• Objetivos de negocio y criterio de éxito: describe las metas que se esperan
alcanzar desde el punto de vista del negocio, así como medidas que determinen el
éxito de los resultados.
37
• Inventario de recursos: busca identificar recursos disponibles para el buen
desenvolvimiento del proyecto, incluyendo personal, fuentes de datos, locaciones,
entre otros.
• Requerimientos, suposiciones y limitaciones: describe requisitos para realizar
el proyecto, así como asunciones y condiciones necesarias para lograrlo.
• Riesgos: describe posibles problemas a encontrar durante el desarrollo del
proyecto, y sus posibles soluciones o medidas a tomar.
• Costos y beneficios: el desembolso dinerario del proyecto y su posibles aportes
(tangibles o no).
• Objetivos de la Minería de Datos y criterio de éxito: manifiesta los resultados
del proyecto que permitirán el alcance de los objetivos de negocio, así como
medidas que determinen el éxito de los resultados en términos de Minería de Datos.
• Plan de proyecto: indica las etapas del proyecto, junto con una duración
tentativa que debe tomar en cuenta la cualidad iterativa de la Minería de Datos.
• Apreciación inicial de herramientas y técnicas: describe los instrumentos que
probablemente sean utilizados.
5.2.2 Entendimiento de los datos
Esta fase comienza con la obtención de los datos, seguido de ciertas actividades para
familiarizarse e identificar problemas en los mismos. Se divide en las siguientes etapas:
•
Reporte inicial de recolección de datos: especifica el origen de los datos,
método de extracción de los mismos y problemas encontrados durante el proceso.
•
Reporte de descripción de datos: abarca la descripción específica de los datos,
incluyendo unidades utilizadas, códigos, etc.
•
Reporte de exploración de datos: explica cualquier evento u observación
relevante después de hacer una exploración inicial a los datos.
•
Reporte de calidad de los datos: describe que tan completa y precisa es la base
de datos.
38
5.2.3 Preparación de los datos
Generalmente, la herramienta de modelado a utilizar necesita los datos en cierto
formato distinto al original y con la mínima cantidad de errores posible, por lo cual deben ser
pre-procesados para obtener resultados óptimos. En esta fase se describen los pasos tomados
para la preparación de los datos y la descripción de sus resultados, incluyendo objetivos del
pre-procesamiento, acciones dirigidas a resolver problemas de calidad de los datos, razones
para la inclusión o exclusión de atributos y otros descubrimientos obtenidos en el proceso.
5.2.4 Modelado
Describe la técnica de modelaje seleccionada y aplicada, así como la calibración de sus
parámetros hasta obtener valores óptimos. Generalmente en esta etapa dicha técnica es
seleccionada entre las muchas que hay, teniendo que retroceder a la etapa anterior para
satisfacer los requisitos de la misma; en el caso de este proyecto ya esta definida en sus
objetivos (Support Vector Machines) por lo cual dicho retroceso no fue necesario. Sus pasos
se pueden resumir en:
•
Asunciones del modelado: define explícitamente las asunciones acerca de los
datos y la herramienta de modelado utilizados.
•
Diseño de prueba: especifica cómo los modelos son creados, probados y
evaluados, para poder cumplir con los objetivos de la Minería de Datos planteados.
•
Descripción del modelo: para cada modelo desarrollado se especifican los
parámetros, condiciones y otras características bajo las cuales fue creado, así como
los resultados obtenidos y su relación con los objetivos propuestos.
•
Apreciación del modelo: describe los resultados obtenidos al aplicar la prueba
especificada anteriormente, a los distintos modelos.
Las últimas dos fases fueron implementadas de forma iterativa, hasta obtener
resultados satisfactorios.
39
5.2.5 Evaluación
Para esta etapa se debe tener un modelo (o modelos) creado que aparentemente posea
alta calidad desde el punto de vista de análisis de datos. Antes de continuar a la etapa de
despliegue, es importante asegurar que los procedimientos seguidos en la obtención de dicho
modelo fueron los adecuados para lograr los objetivos, así como debe revisarse si hubo algún
objetivo importante que no haya sido suficientemente considerado.
Finalmente se concluye si los resultados de la Minería de Datos realizada serán
utilizados, incluyendo recomendaciones en cuanto a próximos pasos a seguir.
5.2.6 Despliegue
El despliegue depende principalmente de las características del proyecto y puede ser,
como en este caso, la redacción de un reporte con los resultados obtenidos a lo largo del
proceso, que puedan ser utilizados cuanto antes para obtener beneficios en el negocio.
CAPÍTULO 6: SOFTWARE UTILIZADO
El presente capítulo describe el software informático empleado en el desarrollo del
proyecto.
6.1 MATLAB
MATLAB es un lenguaje de alto desempeño desarrollado por The MathWorks Inc,
integrando cómputo, visualización y programación en un ambiente matemático. Es empleado
en desarrollo de algoritmos computacionales, adquisición de datos, modelaje, simulación,
análisis de datos, desarrollo de aplicaciones gráficas, entre otros.
Su nombre proviene de “Matrix Laboratory” (laboratorio de matrices), ya que
originalmente fue diseñado para facilitar el manejo de matrices. En la actualidad esa es solo un
pequeño atributo del programa, siendo complementado por extensiones llamadas “toolbox”
que no son mas que secuencias de funciones de MATLAB para resolver problemas
específicos. Existe una gran variedad de áreas que poseen toolbox disponible, incluyendo
procesamiento se señales, sistemas de control, redes neurales, lógica difusa, entre otros. La
Figura 6.1 muestra una vista del programa.
Figura 6.1 Ejemplo de vista del programa MATLAB
41
6.1.1 LS-SVM toolbox
Desarrollado por el grupo KULeuven-ESAT-SCD, el toolbox LS-SVM de MATLAB
es una programación de la metodología de aprendizaje de Support Vector Machines, enfocada
en mínimos cuadrados. Dicho enfoque permite resolver problemas con la condición de
Karush-Kuhn-Tucker (KKT) de forma tal que solo un reducido número de datos de
entrenamiento determinen los márgenes (vectores de soporte).
Permite realizar clasificaciones y regresiones basadas en Support Vector Machines,
ofreciendo características gráficas y de optimización que no están desarrolladas en su totalidad
(no soportan casos de múltiples clases). Además, permite su uso a través de la interfaz
orientada a objetos así como la tradicional interfaz funcional. En la Figura 6.2 se muestra una
gráfica de un ejemplo de clasificación binaria de datos con dos dimensiones.
Figura 6.2 Ejemplo de clasificación binaria con toolbox LS-SVM
42
6.2 SPSS
SPSS es una herramienta estadística desarrollada por SPSS Inc. que permite realizar
una gran variedad de análisis de datos, a la vez permitiendo modificarlos, transformarlos y
graficarlos. Dichos datos conforman una matriz con valores, ya sean categóricos (nominales u
ordinales) o escalares, como se muestra en las Figuras 6.3 (variables región y ventas96
respectivamente).
Figura 6.3 Ejemplo de vista de datos con valores categóricos y escalares en SPSS
Entre los análisis más importantes que provee SPSS se encuentran los siguientes:
• Análisis Factorial: intenta identificar variables subyacentes o factores, que
expliquen la configuración de las correlaciones dentro de un conjunto de
variables. Se suele utilizar en la reducción de los datos para identificar un
pequeño número de factores que explique la mayoría de la varianza observada en
un número mayor de variables manifiestas.
• Análisis de Conglomerados Jerárquico: este procedimiento intenta identificar
grupos relativamente homogéneos basándose en las características seleccionadas,
mediante un algoritmo que comienza con cada caso (o cada variable) en un
conglomerado diferente y combina los conglomerados hasta que sólo queda uno.
43
• Análisis de Conglomerados de K-medias: intenta identificar grupos de casos
relativamente homogéneos basándose en características seleccionadas, utilizando
un algoritmo que puede gestionar un gran número de casos, aunque requiere que
el usuario especifique el mismo. Además se puede especificar los centros
iniciales de los conglomerados si se conoce de antemano dicha información.
• Procedimiento MLG Multivariante: proporciona un análisis de regresión y un
análisis de varianza para variables dependientes múltiples por una o más
covariables o variables de factor.
• Análisis de regresión: estima la relación lineal entre una variable dependiente y
una o más variables independientes.
• Análisis de varianza o ANOVA: comparación de la varianza muestral estimada
a partir de las medias de los grupos respecto a la estimada dentro de dichos
grupos.
6.3 QUANVERT
Quanvert es un software desarrollado por SPSS Inc. que permite la tabulación de datos,
y es empleado para proporcionar los resultados de una investigación cuantitativa. Además,
posee la capacidad de exportar los mismos a SPSS ya que son hechos por la misma compañía.
La Figura 6.4 muestra una vista del programa en la cual se puede apreciar del lado derecho la
lista de variables medidas en el estudio, y en el izquierdo las especificaciones de la tabulación.
44
Figura 6.4 Ejemplo de vista del programa Quanvert
CAPÍTULO 7: RESULTADOS OBTENIDOS
En este capítulo se exponen y discuten los resultados obtenidos al llevar a cabo la
metodología descrita en el Capítulo V.
7.1 REVISION BIBLIOGRAFICA
Luego de investigar a profundidad el sistema de aprendizaje Support Vector Machines,
así como su rol en la creación de máquinas de aprendizaje, se obtuvo el conocimiento
necesario para llevar a cabo el proyecto. Además se estudió las técnicas de minería de datos
necesarias para la preparación de los datos disponibles. En el Capítulo IV se expuso un
resumen del conocimiento adquirido en esta etapa, la cual tuvo una duración de
aproximadamente 7 semanas.
7.2 DESARROLLO DEL PROYECTO
Una vez familiarizado con el tema se siguió el modelo CRISP-DM descrito
anteriormente para el desarrollo del proyecto. Las etapas con sus frutos se presentan a
continuación.
7.2.1 Entendimiento del negocio
Desde el año 2003, la unidad de Cuidado Bucal de Procter & Gamble Servicios
Latinoamérica ha tenido un gran auge en el segmento de pastas dentales en México bajo su
marca principal Crest, en un mercado ampliamente dominado por Colgate. Esto ha sido el
resultado de varios esfuerzos de mercadeo para renovar la imagen de la marca e innovar en la
creación de productos que, siguiendo los lineamientos y propósitos de la compañía, ayuden a
mejorar la vida de los consumidores los cuales recompensarán dicho esfuerzo comprando los
productos.
Hasta la fecha, las iniciativas de nuevos productos de la marca Crest en México se han
basado en el desempeño de los mismos y su aceptación por parte de los consumidores, la cual
46
es capturada a través de estudios realizados por el departamento de Investigación de Mercado.
Además, la publicidad y distribución de los mismos no han sido optimizadas por la falta de un
mercado blanco (target) a quien dirigir los esfuerzos realizados. Esto implica un mal uso de
los fondos destinados a dichas áreas, así como un enfoque fuera de lo deseado al no estar
completamente centrado en el consumidor.
Los objetivos de negocio planteados ante la situación descrita son:
•
Producir dentífricos diseñados para una población específica, la cual al verse
identificada y satisfecha con los mismos procederán a adquirirlos.
•
Aumentar en índice de retorno de inversión ROI, a través de la optimización
de los gastos en publicidad y distribución.
•
Determinar la combinación óptima de las componentes del mercadeo para ser
más eficientes.
•
Lograr un posicionamiento sólido en el mercado de pastas de dientes en
México, atrayendo a la mayor cantidad de consumidores que actualmente
compran Colgate.
Al cumplir con dichos objetivos de negocio, se espera que las ventas de productos
Crest así como sus márgenes de ganancia aumenten. Cabe acotar que por razones de
confidencialidad de la empresa, las medidas precisas de éxito de los objetivos expuestos no
pueden ser divulgadas.
Para alcanzar dichos objetivos, el departamento de Investigación de Mercado de la
unidad de Cuidado Bucal decidió llevar a cabo la segmentación del mercado de pastas
dentales, utilizando una serie de 295 atributos provistos por la unidad de Cuidado Bucal del
GBU de Norte América. Dichos atributos son preguntas que determinan características
psicográficas, demográficas, actitudinales y emocionales de los consumidores, y se incluyeron
en una encuesta realizada entre una muestra representativa de la población mexicana en Mayo
del 2005 de 895 personas. Los resultados de dicho estudio constituyen el recurso principal
para la realización del proyecto, además del personal perteneciente al departamento de
Investigación de Mercado.
47
Cabe destacar que regularmente en los estudios realizados por el departamento de
Investigación de Mercado, el número de entrevistas sobre una muestra representativa de la
población es de 300, pero dada la importancia estratégica de este proyecto se decidió triplicar
dicha cifra para obtener resultados más precisos.
El éxito del proyecto depende altamente de la suposición de que los datos
proporcionados por los consumidores a través de las encuestas son verídicos. Al mismo
tiempo debe tomarse en cuenta la limitación de que dichos datos serán válidos por un tiempo
determinado (generalmente 2 a 3 años), ya que las variables medidas tienden a cambiar en la
población.
El costo monetario constituye información confidencial, pero sus beneficios son
considerables al aumentar las ganancias del negocio, tanto por volumen de ventas, como por
optimización de recursos empleados para lograr las mismas.
La Minería de Datos, como herramienta para el procesamiento de datos y parte del
proceso de descubrimiento de conocimiento, fue planteada como instrumento para lograr los
siguientes objetivos:
•
Lograr una segmentación efectiva de la población, entendiéndose por efectiva
que tengan sentido en el contexto de mercadeo.
•
Utilizar los resultados de dicha segmentación como base para la creación de un
método que permita identificar a los distintos grupos en futuros estudios del
departamento de Investigación de Mercado.
El principal problema para lograr el segundo objetivo es que en futuros estudios, cuyos
propósitos ya no serán la segmentación de la población (ej. calificación de nuevos productos),
no será posible añadir la gran cantidad de atributos utilizados por este proyecto a las preguntas
concernientes a la nueva investigación. Además, para lograr la clasificación de entrevistados
con combinaciones de características no vistas en la segmentación inicial, es necesario la
utilización de un sistema de aprendizaje con buenas propiedades de generalización.
48
El criterio de éxito propuesto es obtener la aprobación de los expertos de mercadeo en
cuanto a la coherencia de la segmentación de la población, así como lograr la clasificación de
datos no utilizados en el entrenamiento del sistema de aprendizaje a modelar, a partir de
menos de 15 atributos, con un más de 95% de efectividad. Para lograr esto, se propuso el
siguiente plan basado en la metodología expuesta en el Capítulo V:
•
Entendimiento de los datos (1 semana): familiarización con los datos
resultantes del estudio realizado, así como la descripción de sus valores y
unidades.
•
Preparación de los datos (4 semanas): dado que la segmentación especificada
en los objetivos será utilizada para el modelado del sistema de aprendizaje, fue
considerada parte de esta etapa, siendo un sub-problema de Minería de Datos a
través de la técnica de agrupamiento. Además, para lograr disminuir la cantidad
de variables empleadas, el análisis de componentes principales fue considerado
de forma similar en esta fase.
•
Modelado (5 semanas): creación de un modelo de Support Vector Machines
para la clasificación de los datos, partiendo de los kernels más exitosos en áreas
diversas.
•
Evaluación (1 semana): revisión exhaustiva de los métodos empleados y sus
resultados, involucrando a expertos de Investigación de Mercado y Mercadeo
de la empresa.
•
Despliegue (2 semanas): elaboración del informe con los resultados obtenidos,
correspondiente al presente libro final del proyecto de pasantía.
Las técnicas y herramientas empleadas fueron descritas en el Capítulo IV.
7.2.2 Entendimiento de los datos
La fuente principal de datos para la realización del proyecto son los resultados de las
895 entrevistas realizadas por el departamento de Investigación de mercado, constituyendo
cada una de ellas una fuente puntual de información.
49
Los datos fueron proporcionados en formato Quanvert (extensión pkd). Este programa
permite elaborar tablas con los resultados pero no posibilita el tratamiento de los datos, por lo
que se utilizó su propiedad de exportación a SPSS.
Una vez en formato SPSS, se pudo apreciar las siguientes características de los datos:
•
Corresponden a medidas ordinales de tipo numérico.
•
Sus valores válidos, con su correspondiente significado ante preguntas de
conformidad son: -2,00 “Fuertemente en desacuerdo”, -1,00 “En desacuerdo”,
,00 “Ni de acuerdo ni en desacuerdo”, 1,00 “De acuerdo” y 2,00 “Fuertemente
de acuerdo”.
•
Los valores -9901,00 y -99,99 corresponden a datos perdidos o no contestados
por los entrevistados, considerados como inválidos.
•
Cada atributo posee un nombre código así como una etiqueta. Este último
corresponde a la pregunta explicita realizada en el estudio, siendo la primera
una abreviación de la misma. Por razones de confidencialidad de la empresa,
estos no podrán ser asentados en este informe y en lo sucesivo serán
distorsionadas las imágenes que los contengan.
En la Figura 7.1 se puede apreciar parte del análisis de estadísticos descriptivos
realizado, el cual incluye para cada atributo el número de casos válidos (N), mínimo, máximo,
media, desviación estándar o típica y varianza. Solo se muestra una parte debido a la gran
cantidad de atributos.
50
Figura 7.1 Estadísticos descriptivos de los datos disponibles (primeros 7 atributos)
Este análisis permitió observar las medias y desviaciones estándares de cada atributo,
proporcionando una exploración de los resultados arrojados por el estudio, así como junto a la
varianza, se pudo tener un primer acercamiento en cuanto a cuales características podrían ser
discriminantes al momento de separar grupos y cuales no. Debido a la gran cantidad de
atributos que presentaron poca varianza en relación a un grupo de aproximadamente 30 que
desatacó con valores superiores, se concluyó que el análisis de componentes principales
planteado en el plan propuesto tenía altas probabilidades de éxito.
La calidad de los datos, tomando en cuenta las suposiciones expuestas anteriormente,
se pudo valorar a través de la cantidad de casos válidos. En promedio, cada atributo cuenta con
mas del 99.7% de datos válidos, pero al investigar más a fondo solo el 79% de los individuos
51
entrevistados poseen datos válidos para todos los atributos. Esta última cifra representa mas
adecuadamente la calidad de los datos tomando en cuenta los objetivos del proyecto, ya que
para realizar una segmentación efectiva de personas deben tomarse en cuenta todas las
características medidas, por lo que la ausencia de una de ellas representa un problema.
7.2.3 Preparación de los datos
Debido a la elevada cantidad de entrevistas con datos inválidos descubiertos en la
etapa anterior, y tomando en cuenta que la cantidad total de entrevistas realizadas es tres veces
mayor que lo usual, se decidió utilizar solo aquellas que fueran completamente válidas para
asegurar una segmentación efectiva. Con esto se eliminaron 192 fuentes puntuales de datos,
quedando 703 restantes para las siguientes etapas.
Una vez solventado el problema de la calidad de los datos, se continuó a la etapa de
segmentación a través de la técnica de agrupamiento. Utilizando el programa estadístico SPSS
se realizaron varios análisis de agrupamiento jerárquico para obtener una idea de la cantidad
de grupos separables en los datos.
Se utilizaron los métodos de medición de distancia por centroide y por promedio de
relación entre grupos, para evitar en lo posible la influencia de datos aislados. No se obtuvo
diferencia entre ambos resultados y el dendograma resultante se muestra en la Figura 7.2 (solo
la parte final ya que completo son 16 páginas). Este muestra como existen 4 grupos
principales, siendo uno de ellos demasiado pequeño (menos del 0,5% de las fuentes de datos).
52
Figura 7.2 Dendograma de los datos (parte final)
Luego de eliminar el insignificante grupo hallado (restando 700 fuentes de datos), y
tomando en cuenta que la solución aparente es de 3 grupos, se realizó un agrupamiento Kpromedios ya que proporciona más información que el jerárquico pero necesita el número de
conglomerados. El mismo fue repetido hasta alcanzar el número de iteraciones en el cual las
53
distancias entre los centros de los conglomerados no cambiasen, obteniéndose otra fuente de
datos extraordinario que no permitía la separación de los 3 grupos deseados (Figura 7.3).
Figura 7.3 Resultados del agrupamiento K-promedios No. 1
Se identificó y eliminó el caso problemático y se repitió el análisis. El resultado de
número de casos en cada conglomerado se muestra en la Figura 7.4, y son muy similares a los
tamaños sugeridos por el agrupamiento jerárquico; la pequeña diferencia se puede explicar por
la exclusión de los 4 casos considerados como ruido.
Figura 7.4 Resultado del agrupamiento K-promedios No. 2
54
Utilizando los centros de los conglomerados finales (parte de la cual se muestra en la
Figura 7.5), se elaboró un reporte con las características principales de cada grupo en cuanto a
los atributos evaluados, el cual fue discutido con el departamento de Mercadeo. Se concluyó
que los grupos poseen características suficientemente diferentes y aprovechables, por lo que
fue validado.
Figura 7.5 Centros de cada conglomerado para cada atributo evaluado (primeros 9)
55
Con esto se obtuvo una lista final de pertenencia de cada caso o fuente de datos a cada
grupo con sus respectivas distancias a los centros de los mismos, parte de la cual se muestra en
la Figura 7.6. A partir de ésta se creó una variable de pertenencia de conglomerado para
utilizarse en la siguiente etapa.
Figura 7.6 Pertenencia a los conglomerados de cada fuente de datos (primeros 30)
La variable de pertenencia de conglomerados fue utilizada como variable dependiente
en el análisis de componentes principales, el cual al definir la combinación de los atributos que
56
abarcan la mayor cantidad de varianza sobre cada conglomerado determina cuales tienen
mayor influencia. En la Tabla 7.1 se muestran parte de los resultados para cada conglomerado.
Grupo 1
atributo 1
atributo 2
atributo 3
atributo 4
atributo 5
atributo 6
atributo 7
atributo 8
atributo 9
atributo 10
atributo 11
atributo 12
atributo 13
atributo 14
atributo 15
atributo 16
atributo 17
atributo 18
atributo 19
atributo 20
atributo 21
atributo 22
atributo 23
atributo 24
atributo 25
atributo 26
atributo 27
atributo 28
atributo 29
atributo 30
Grupo 2
Bruta
Reescalada
,381
,368
,165
,180
,093
,277
,105
,400
,161
,244
,241
,351
,457
,358
,223
,299
,168
,235
,146
,094
,225
,330
,256
,179
,323
,268
,208
,282
,238
,139
,381
,361
,187
,211
,127
,340
,145
,410
,197
,292
,281
,401
,491
,396
,277
,312
,209
,271
,173
,129
,304
,379
,302
,241
,344
,280
,219
,297
,274
,158
Bruta
,060
,254
,183
,096
,061
,200
,328
,094
,256
,298
,112
,159
,112
,242
,354
,047
,160
-,208
,331
,382
,138
,128
,087
,252
-,012
-,054
,487
,347
,331
,281
Grupo 3
Reescalada
,098
,324
,199
,095
,066
,255
,411
,112
,301
,398
,114
,181
,153
,283
,435
,055
,162
-,243
,339
,388
,142
,178
,110
,305
-,016
-,088
,480
,362
,394
,374
Bruta
Reescalada
,111
-,085
,051
,014
,103
,131
,215
-,014
,290
,286
,126
,174
-,050
,153
,204
-,057
,009
-,114
,143
,257
,207
-,080
,169
,231
-,078
-,170
,311
,085
,209
,220
,137
-,094
,057
,015
,117
,169
,291
-,015
,323
,378
,145
,191
-,061
,184
,242
-,064
,010
-,127
,155
,325
,246
-,095
,199
,310
-,096
-,196
,369
,097
,234
,227
Tabla 7.1 Matriz de componentes para cada conglomerado (primeros 30 atributos)
Al analizar la matriz de componentes se seleccionaron 18 atributos que sobresalieron
por tener alta influencia sobre los grupos establecidos en la segmentación (los 6 mayores de
cada grupo) y se muestran en la Tabla 7.2.
57
Grupo 1
,491
,476
,472
,438
,435
,435
,364
,399
,188
,219
,277
,122
,369
,297
,225
,315
,196
,288
atributo 13
atributo 56
atributo 50
atributo 36
atributo 45
atributo 107
atributo 31
atributo 68
atributo 94
atributo 27
atributo 15
atributo 288
atributo 87
atributo 86
atributo 89
atributo 121
atributo 95
atributo 125
Grupo 2
,153
,109
,283
,203
,093
,101
,489
,486
,481
,480
,435
,427
,405
,184
,176
,384
,362
,263
Grupo 3
-,061
-,188
,045
,218
-,019
,152
,184
,219
,358
,369
,242
,380
,438
,428
,425
,421
,415
,395
Tabla 7.2 Componentes de los atributos seleccionados para cada conglomerado
Al hacer un estudio de correlaciones bivariadas (Tabla 7.3) se determinó que sólo 15
atributos eran independientes (correlación < 0,3 en relación a los otros atributos), eliminando
el 50, 87 y 94. Además se decidió prescindir del atributo 13 por tener 4 correlaciones mayores
a 0,2.
Atributos
13
15
27
31
36
45
50
56
68
86
87
89
94
95
107
121
125
288
13
1,000
,176
,098
,140
,214
,160
,266
,239
,105
,029
,041
,032
,053
,013
,258
,004
,083
-,006
15
27
31
36
45
50
56
68
1,000
,187
,154
,083
,036
,060
,078
,069
,099
,129
,156
,089
,060
,097
,130
,127
,092
1,000
,218
,114
,192
,169
,057
,196
,170
,214
,076
,235
,154
,160
,164
,185
,160
1,000
,120
,172
,190
,125
,197
,064
,109
,038
,133
,054
,214
,102
,097
,080
1,000
,149
,205
,126
,104
,096
,137
,122
,096
,021
,169
,093
,053
,012
1,000
,240
,183
,147
-,007
,074
,057
,110
,041
,213
,001
,045
,025
1,000
,336
,196
,090
,083
,035
,153
-,017
,303
,057
,109
,059
1,000
,178
,080
-,049
,048
,083
-,109
,214
-,048
-,009
,093
1,000
,130
,142
,124
,193
,106
,141
,122
,125
,067
58
Tabla 7.3 Matriz de correlaciones bivariadas (Continúa en la siguiente página)
Atributos
13
15
27
31
36
45
50
56
68
86
87
89
94
95
107
121
125
288
86
87
89
94
95
107
121
125
288
1,000
,313
,128
,100
,125
,083
,139
,137
,143
1,000
,229
,141
,221
,080
,330
,251
,200
1,000
,220
,150
,060
,195
,077
,098
1,000
,414
,109
,146
,119
,173
1,000
-,021
,197
,148
,157
1,000
,080
,106
,102
1,000
,213
,149
1,000
,140
1,000
Tabla 7.3 Matriz de correlaciones bivariadas (Continuación)
Con lo anterior se cumplió con la selección de menos de 15 atributos a tratar en el
modelado, como se había planteado.
7.2.4 Modelado
En esta etapa se utilizó el toolbox de Matlab LS-SVMlab para crear un modelo de
Support Vector Machines que separase los 3 grupos. Para lograrlo se empleó inicialmente la
técnica “Holdout” por ser computacionalmente menos exigente y por ende, más apropiada
para esta etapa (por basarse en la iteración), utilizando los primeros 500 casos para entrenar a
la maquina de aprendizaje con distintos valores de gamma (factor de generalización), para
luego evaluar el desempeño de cada modelo con los 199 casos restantes.
Inicialmente se modeló empleando distintos kernels reconocidos por ser exitosos en
distintas aplicaciones, utilizando cada atributo como una dimensión y valores de gamma y
sigma que pudiesen arrojar diferencias significativas entre si (con valor máximo de gamma
100 ya que valores superiores implican tiempos de procesamiento no meritorios). La Figura
7.7 muestra los resultados obtenidos, destacando aquellos arrojados al utilizar el Kernel Lineal
59
con 77,4% de efectividad sin importar el nivel de generalización. A su vez se comprobó el
pobre desempeño del Kernel RBF con datos no continuos con poco más de 60% de eficacia en
el mejor de sus casos. El Kernel Polinomial (resultados no mostrados en la Figura 7.7), resultó
ser el menos eficiente, al clasificar a todos los casos como pertenecientes al grupo 1,
mostrando su inhabilidad de distinguir los grupos en el entrenamiento.
Resultados obtenidos con distintos Kernel y
parámetros sobre los datos de prueba
80.0%
70.0%
60.0%
50.0%
40.0%
30.0%
20.0%
10.0%
LIN g=0.1
LIN g=1
LIN g=10
LIN g=100
RBF sig=0.2 g=0.1
RBF sig=0.2 g=1
RBF sig=0.2 g=10
RBF sig=0.2 g=100
RBF sig=0.4 g=0.1
RBF sig=0.4 g=1
RBF sig=0.4 g=10
RBF sig=0.4 g=100
0.0%
Correctas
Incorrectas
No clasificados
Figura 7.7 Resultados obtenidos con distintos Kernel y parámetros sobre los datos de prueba
Al obtener los resultados presentados para los Kernels comúnmente utilizados en el
sistema de aprendizaje de Support Vector Machines, se clarificó la necesidad de crear un
espacio característico que lograse separar efectivamente los datos correspondientes a grupos
distintos, ya que los objetivos planteados no fueron alcanzados. Para lograrlo, se probaron
distintas funciones que modificasen los datos originales, cuyos los resultados fueron
empleados como datos de entrada en la creación del modelo. De esta forma se pudo iterar con
menor complejidad en la creación de dicha función a sabiendas que requeriría mayor esfuerzo
60
computacional, ya que no se poseía la experiencia necesaria con el tipo de datos para la
creación de un Kernel que tuviese implícita la transformación.
Inicialmente se realizó un análisis de componentes principales utilizando solo los 14
atributos determinados, siendo la variable de pertenencia de conglomerado la variable de
selección. Este proporcionaría la influencia de cada atributo en la pertenencia a cierto
conglomerado, con lo cual se ponderarían los resultados como se sugiere en [Cristianini y
Shawe-Taylor, 2000]. El resultado del análisis de componentes principales se muestra en la
Tabla 7.4.
Atributos
Finales
Grupo 1
Grupo 2
Grupo 3
1
2
3
4
5
6
7
8
9
10
11
12
13
14
-0,0784
0,4081
0,5100
0,5242
0,2193
0,3951
0,5725
0,1673
-0,1112
0,4147
0,1769
-0,3403
0,4944
-0,1960
0,2503
-0,0595
0,2593
-0,1528
0,1875
0,6121
0,1403
0,3362
-0,2341
0,4515
0,5975
0,3383
0,5820
-0,2584
0,5075
0,2398
0,3063
0,2325
0,2457
0,3330
0,3719
0,4291
0,3611
0,6336
0,6984
0,4909
0,5948
0,4767
Tabla 7.4 Componentes de los atributos para cada conglomerado
Al ponderar para cada conglomerado el valor de cada atributo y sumarlos se
obtuvieron las 3 dimensiones utilizadas para modelar varias SVM con los mismos parámetros
que en el caso anterior. En la Figura 7.8 se muestran la distribución de los datos en el espacio
característico creado, en el cual se pueden observar los 3 conglomerados con cierto grado de
separación.
61
Figura 7.8 Distribución de los datos en el espacio característico de componentes principales
En la Figura 7.9 se grafican los resultados obtenidos con los datos de prueba,
manifestando un mejor desempeño del Kernel RBF sobre datos reales, especialmente para una
dispersión sig=0,2 y una generalización gamma=10 (78,4%), y 0,4 y 100 respectivamente
(76,4%). La razón de la equivalencia de los 2 casos anteriores se debe a que la segunda amplía
el tamaño de la distribución gaussiana pero es menos exigente con los límites. Cabe destacar
que ambas soluciones presentan menos del 1% de casos no clasificables, que a pesar de ser
insignificante no es nula. El Kernel Lineal desmejora significativamente sus resultados con
este espacio característico presentando 40,7% de eficacia y más de 13% de casos no
clasificables. Por su parte el Kernel Polinomial falló de nuevo en poder discriminar los
conglomerados.
62
Resultados obtenidos con especio característico de
componentes principales con distintos Kernel y
parámetros sobre los datos de prueba
80.0%
70.0%
60.0%
50.0%
40.0%
30.0%
20.0%
10.0%
LIN g=0.1
LIN g=1
LIN g=10
LIN g=100
RBF sig=0.2 g=0.1
RBF sig=0.2 g=1
RBF sig=0.2 g=10
RBF sig=0.2 g=100
RBF sig=0.4 g=0.1
RBF sig=0.4 g=1
RBF sig=0.4 g=10
RBF sig=0.4 g=100
0.0%
Correctas
Incorrectas
No clasificados
Figura 7.9 Resultados obtenidos con espacio característico de componentes principales con distintos Kernel y
parámetros sobre los datos de prueba
Se llevaron a cabo varios intentos de mejorar la separación de los datos en este espacio
característico, incluyendo normalizaciones lineales y exponenciales. La primera se empleó ya
que al analizar los datos procesados por el espacio característico, fue evidente que no existía
relación alguna entre cada uno de los casos tal que se pudiese observar un patrón; para
resolverlo se normalizaron las dimensiones para que su suma fuese 1. Esto no logró llevar todo
a una misma base como se muestra en la Figura 7.10, debido a que al haber valores negativos
no existían límites para que la suma fuese 1. Es por lo anterior que se empleó la normalización
exponencial (la suma de las exponenciales de cada dimensión igual 1 para cada caso), con la
cual se obtendrían datos más separados dentro de un rango establecido (todos los valores
positivos), logrando la distribución de la Figura 7.11. Si bien para en caso de las componentes
principales no hubo mejora alguna con estas modificaciones, se mencionan por su importancia
en espacios característicos creados posteriormente.
63
Figura 7.10 Distribución de los datos en el espacio característico de componentes principales con normalización
lineal a 1
Figura 7.11 Distribución de los datos en el espacio característico de componentes principales con normalización
exponencial a 1
64
El espacio característico creado a partir de las componentes principales, si bien es
cierto que mejoró significativamente el desempeño del Kernel RBF, no logró superar de forma
contundente el resultado anterior del Kernel Lineal y mucho menos alcanzar el objetivo de
95% de eficacia. Por dicho motivo se iteró en la búsqueda de un Kernel que lo lograse,
haciendo uso de análisis de componentes principales desde 2 hasta 6 componentes por
conglomerado, ponderación por el inverso de la distancia al promedio de los conglomerados,
regresiones lineales, logarítmicas, entre otros.
Todos los anteriores fallaron en lograr una mejora excepto por la regresión lineal; la
misma se llevó a cabo para cada conglomerado, asignando el valor 1 a la función a aproximar
si el caso perteneciese a ese grupo y 0 en caso contrario. Es importante señalar que para dicha
regresión sólo se utilizaron los casos pertenecientes a los datos de entrenamiento, para de esta
forma comprobar su validez sobre casos no estudiados.
A partir de dicho análisis se obtuvo 3 dimensiones con componentes para cada
atributo, además de una constante. Los valores obtenidos no se muestran por razones de
confidencialidad de los datos de la empresa.
Con los componentes obtenidos a raíz de dicha regresión se logró la distribución de los
datos de la Figura 7.12, en la cual se observan los conglomerados aún mas separados que con
el espacio característico de componentes principales.
65
Figura 7.12 Distribución de los datos en el espacio característico de regresión lineal
Con este espacio característico se modelaron las SVM con los mismos parámetros
usados anteriormente para establecer comparaciones. Los resultados se muestran en la Figura
7.13 revelando que se obtuvo modelos que superaron el 90% de clasificaciones correctas, y
específicamente para valores de gamma=1 y sigma=0,4, se obtuvo 94,5% de eficiencia con
0,5% de casos no clasificados. Nuevamente se hizo evidente la superioridad en desempeño del
Kernel RBF sobre el lineal para datos con valores reales, así como sobre el polinomial que
presentó el mismo problema de los espacios característicos anteriores. Los modelos RBF más
exitosos sobre los datos de prueba fueron aquellos con poca generalización (gamma 1 y 10),
reflejando que los datos se encuentran lo suficientemente separados como para prescindir de
una generalización computacionalmente demandante como lo es gamma=100 (tiempo de
procesamiento elevado), pero a la vez no suficiente para prescindir completamente de ella
(gamma=0,1).
66
Resultados obtenidos con especio característico de
regresión con distintos Kernel y parámetros sobre los
datos de prueba
100.0%
90.0%
80.0%
70.0%
60.0%
50.0%
40.0%
30.0%
20.0%
10.0%
LIN g=0.1
LIN g=1
LIN g=10
LIN g=100
RBF sig=0.2 g=0.1
RBF sig=0.2 g=1
RBF sig=0.2 g=10
RBF sig=0.2 g=100
RBF sig=0.4 g=0.1
RBF sig=0.4 g=1
RBF sig=0.4 g=10
RBF sig=0.4 g=100
0.0%
Correctas
Incorrectas
No clasificados
Figura 7.13 Resultados obtenidos con espacio característico de regresión con distintos Kernel y parámetros sobre
los datos de prueba
Finalmente se trataron los datos con la normalización exponencial mencionada
anteriormente, obteniendo la distribución de la Figura 7.14. En la misma se observa una
evidente separación de los grupos, lo cual pudiese augurar un mejor desempeño de los
clasificadores.
67
Figura 7.14 Distribución de los datos en el espacio característico de regresión lineal con normalización
exponencial
La Figura 7.15 revela los resultados del modelaje de varias SVM utilizando el espacio
característico de regresión lineal con normalización exponencial. En ella se observa que el
desempeño tanto del Kernel RBF como el Lineal, supera el objetivo de 95% de clasificaciones
correctas. Cabe acotar que los modelos resultantes del Kernel Lineal presentaron un 1,5% de
casos no clasificados, mientras que para el RBF existieron 5 casos con 99,5% de efectividad y
ningún caso no clasificable (sigma=0,2 con gamma 1 y 10, sigma 0,4 con gamma 1, 10 y 100).
68
Resultados obtenidos con especio característico de
regresión normalizado EXPONENSIALcon distintos
Kernel y parámetros sobre los datos de prueba
100.0%
90.0%
80.0%
70.0%
60.0%
50.0%
40.0%
30.0%
20.0%
10.0%
LIN g=0.1
LIN g=1
LIN g=10
LIN g=100
RBF sig=0.2 g=0.1
RBF sig=0.2 g=1
RBF sig=0.2 g=10
RBF sig=0.2 g=100
RBF sig=0.4 g=0.1
RBF sig=0.4 g=1
RBF sig=0.4 g=10
RBF sig=0.4 g=100
0.0%
Correctas
Incorrectas
No clasificados
Figura 7.15 Resultados obtenidos con espacio característico de regresión con normalización exponencial para
distintos Kernel y parámetros sobre los datos de prueba
A partir de los 5 casos en los que se obtuvo la mayor tasa de clasificaciones correctas
sin casos no clasificables, se llevó a cabo una validación cruzada para determinar cual era el
más óptimo. La misma consistió en entrenar a la SVM con los mismos parámetros pero con
distintos grupos de datos de entrenamiento y de prueba. Como los resultados obtenidos hasta
este punto estaban basados en los primeros 500 casos como data de entrenamiento y los
restantes 199 de prueba, se realizaron 2 nuevos análisis utilizando los primeros 199 casos
como data de prueba y el resto de entrenamiento, al igual que con los segundos 199 casos. En
la Tabla 7.5 se muestran los resultados de las 3 validaciones y el promedio para cada caso (no
se muestran las tasas de no clasificados por ser inexistentes en todos), el cual establece que los
valores óptimos del Kernel RBF para los datos procesados por el espacio característico de
regresión lineal con normalización exponencial son gamma=100 y sigma=0,4, con un
promedio de 99,16% de clasificaciones correctas y 0% de datos no clasificados.
69
Kernel RBF
Validación 1
Validación 2
Validación 3
Promedio
sigma=0,2
gamma=1 gamma=10
99,50%
99,50%
95,98%
98,99%
95,48%
96,98%
96,98%
98,49%
gamma=1
99,50%
97,99%
96,98%
98,16%
sigma=0,4
gamma=10 gamma=100
99,50%
99,50%
98,99%
98,99%
97,99%
98,99%
98,83%
99,16%
Tabla 7.5 Resultados de la validación cruzada para el Kernel RBF con espacio característico de regresión con
normalización exponencial
Cabe acotar que aunque para los 5 casos estudiados en la validación cruzada todos
cumplieron con el criterio de éxito propuesto para medir el alcance de los objetivos de la
Minería de Datos planteados, el que aplicaba mayormente la generalización asumiendo una
distribución gaussiana no tan estrecha de los datos fue el que tuvo mejor desempeño. Lo
anterior pone de manifiesto la importancia de la generalización como característica
fundamental de Support Vector Machines.
Finalmente se entrenó a la máquina con los 699 casos con los parámetros y espacios
característicos, obteniendo una SVM con valores de polarización (b) y vector α con los
cuales se clasificarán a las personas en futuros estudios de mercado. Dichos valores no se
muestran por razones de confidencialidad de la empresa.
7.2.5 Evaluación
En la sección anterior se mostró como se obtuvo un modelo óptimo para la
clasificación de la población a partir de pocos parámetros. Al revisar los procedimientos
empleados se concluye que los mismos, si bien tuvieron características iterativas por la poca
información disponible sobre el procedimiento más adecuado, se llevaron a cabo con el
cuidado debido de no alterar la esencia de los datos, así como de asegurar su aplicabilidad
sobre combinaciones de atributos distintas a las tratadas en este proyecto. Además se
considera que los objetivos de la minería de datos planteados fueron alcanzados, así como se
proporcionan las herramientas para lograr los objetivos de negocio.
Los próximos pasos a seguir constituyen desde el punto de vista de la Minería de datos
la creación de un Kernel que contenga implícito el espacio característico creado, evitando el
efecto de la dimensionalidad y concentrando el esfuerzo computacional sólo en el producto
70
interno, además de la programación de una representación gráfica de los resultados. Desde el
punto de vista del Negocio son el enfoque de las estrategias de mercadeo sobre el grupo de la
población más susceptible a cambiarse de su marca de pasta de dientes tradicional (Colgate),
determinado por las características de los 3 conglomerados resultantes de este proyecto, así
como el diseño de nuevos productos diseñados para cubrir las necesidades de los mismos.
7.2.6 Despliegue
El despliegue de los resultados obtenidos con el desarrollo de éste proyecto fueron la
exposición de los mismos a los directivos de Investigación de Mercado de la unidad de
Cuidado Bucal de Procter & Gamble Servicios Latinoamérica, así como la creación de este
informe. A raíz del primero, dicho departamento incluirá el grupo preguntas determinantes
sugeridas en sus próximos estudios cuantitativos, para llevar a cabo la validación de la
metodología en cuanto a impacto en el negocio.
CAPÍTULO 8: CONCLUSIONES Y RECOMENDACIONES
Este capítulo enmarca las experiencias adquiridas a través de la realización del
proyecto, así como a la vez expone la aplicabilidad de los resultados obtenidos. Además,
finaliza con sugerencias para futuros trabajos en el área.
Luego de finalizado el proyecto de Implementación de Support Vector Machines para
reconocimiento de segmentos de la población basados en patrones de consumo y
características psicográficas, se concluye que los todos los objetivos planteados fueron
alcanzados y superados. No solo se exploraron las técnicas de Minería de Datos y las bases
teóricas de Support Vector Machines, sino que se implementaron sobre los datos
suministrados por la empresa, logrando un modelo robusto de reconocimiento.
Específicamente se concluye que:
•
La metodología CRISP-DM empleada proporcionó una clara y profunda visión
del proyecto y sus etapas, tomando en cuenta no solo los pasos necesarios para
el tratamiento de datos, sino también el aspecto gerencial contenidos en los
objetivos de negocio que se desean alcanzar.
•
El análisis de componentes principales proporcionó una reducción significativa
del número de variables necesarias para la identificación de segmentos
homogéneos de datos.
•
El Kernel Lineal posee gran aplicabilidad en la clasificación de datos discretos,
debido a la superioridad demostrada sobre los datos categóricos ordinales
originales en comparación con el RBF y el Polinomial. Lo mismo ocurre para
el Kernel RBF sobre datos continuos (escalares).
•
Los Kernel comúnmente empleados en el modelaje de Support Vector
Machines (Lineal, RBF y Polinomial), no son lo suficientemente efectivos en la
clasificación de los datos originales utilizados en este proyecto. Por esto, la
creación de un dominio característico que ayudase a cumplir los objetivos
planteados fue necesaria.
72
•
La creación de un dominio característico a partir del análisis de componentes
principales que ayudase a cumplir con los objetivos establecidos, fracasó.
•
Los objetivos fueron alcanzados a través de la creación de un dominio
característico de regresión lineal con normalización exponencial, con un
promedio de validación cruzada superior al 99% de efectividad, empleando el
Kernel RBF con parámetros de generalización gamma=100 y de dispersión
sigma=0,4.
•
Se comprobó el alto potencial de Support Vector Machines en el
reconocimiento de segmentos de la población a través de patrones de consumos
y características psicográficas, al obtener más de 95% de efectividad, pero a la
vez evidenciando el rol protagónico de los espacios característicos en dichos
resultados.
•
Se demostró la importancia de la generalización como elemento fundamental
de Support Vector Machines, al tener un importante y generalmente positivo
impacto en los resultados de los modelos generados.
Es importante resaltar que, debido a los excelentes resultados obtenidos ante la
aplicación de la metodología presentada sobre datos reales provenientes de encuestas, sin
precedentes aparentes, la publicación del trabajo realizado se encuentra bajo consideración.
Para trabajos futuros se recomienda:
•
Emplear el modelo CRISP-DM en trabajos que involucren Minería de Datos,
por los motivos expuestos anteriormente.
•
Diseñar una metodología genérica para la creación espacios característicos,
debido a que estos permiten la expansión de las áreas de aplicación de Support
Vector Machines.
•
Evaluar la aplicabilidad de la rama de regresión de Support Vector Machines en
la predicción de consumos de mercados, dadas ciertas características
influyentes
como
macroeconómicos, etc.
publicidad,
distribución,
promociones,
elementos
CAPÍTULO 9: REFERENCIAS BIBLIOGRÁFICAS
[Aguilar, 2002]
R. Aguilar, “Minería de Datos: Fundamentos,
Técnicas y Aplicaciones”, Reprografía Signo,
Salamanca, España (2002)
[Bucherer y Robinson, 2003]
J. Bucherer y L. Robinson, “Effective Targeting:
Unifying Segmentation and Market Structure”,
www.acnielsen.com (2003)
[Burgues, 1998]
C. Burgues, “A tutorial on Support Vector
Machines for Pattern Recognition”, Data Mining
and Knowledge Discovery 2, 121-167 (1998)
[Chapman et al., 1999]
P. Chapman, J. Clinton, R. Kerber, T. Khabaza, T.
Reinartz, C. Shearer y R. Wirth, “CRISP-DM 1.0
step-by-step
data
mining
guide”,
www.crisp-dm.org (1999)
[ClopiNet, 2005]
ClopiNet
Consulting
Company,
www.clopinet.com, “SVM Application List”.
Consultado en mayo de 2005.
[Cristianini y Shawe-Taylor, 2000]
N. Cristianini y J. Shawe-Taylor, “An Introduction
to
Support
Vector
Machines”,
Cambridge
University Press, Cambridge, EUA (2000)
[NRL, 2005]
U.S.
Naval
www.nrl.navy.mil,
Research
“Automatic
Laboratory,
Learning”.
Consultada en abril de 2005)
[P&G, 2005]
Procter & Gamble, www.pg.com, Página principal
de Procter & Gamble. Consultado en septiembre
de 2005.
[Politécnico de Milano, 2005]
Politécnico de Milano, www.elet.polimi.it, “A
Tutorial on Clustering Algorithms”. Consultado
en abril de 2005.
74
[Recklies, 2001a]
D. Recklies, “Why Segmentation?”,
www.themanager.org (2001)
[Recklies, 2001b]
D. Recklies, “Positioning as a Strategic Marketing
Decision”, www.themanager.org (2001)
[Smith, 2002]
L. Smith, “A tutorial on Principal Components
Analysis”, www.kybele.psych.cornell.edu (2002)
[SPSS, 2002]
“Data Analysis with SPSS”, SPSS Inc. (2002)
[Sutton y Barto, 1998]
R. Sutton y S. Barto, “Reinforcement Learning:
An Introduction”, MIT Press, Cambridge, EUA
(1998)