Oscilador a Cristal Controlado por Voltage (VCXO): Estudios

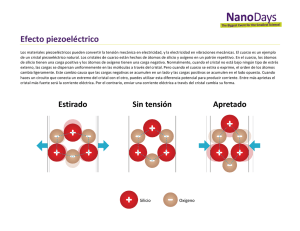
Oscilador a Cristal Controlado por Voltage (VCXO):
Estudios Preliminares para su Integración.
Laureano Bulus
Alumno UNLP
CeTAD, Facultad de Ingeniería de la Universidad Nacional de La Plata,
Calle 48 y 116, La Plata (1900), Bs. As., Argentina.
e-mail: lbulus@barcala.ing.unlp.edu.ar
Abstract. This document presents circuit
considerations that will serve as reference for
constructing a Voltage Controlled Crystal
Oscilator (VCXO). Basic concepts about
oscillators are introduced, as well as
considerations for their design and integration.
Also, are shown measurement results of a discrete
prototype.
Resumen.
Este
documento
presenta
consideraciones que servirán como referencia
para la construcción de un Oscilador a Cristal
Controlado por Tensión (VCXO). Se introducen
conceptos básicos de osciladores así como también
consideraciones para su diseño e integración.
También se muestran resultados de mediciones de
un prototipo discreto.
1. INTRODUCCIÓN
La importancia de los osciladores a cristal en
la electrónica se debe al extremadamente alto Q,
pequeño tamaño y excelente estabilidad frente a
variaciones de temperatura que poseen los
resonadores de cristal de cuarzo.
Con el fin de diseñar un oscilador a cristal
controlado por tensión (VCXO), es indispensable dar
primero una reseña acerca del funcionamiento de los
osciladores. Básicamente, un oscilador puede ser
pensado como un sistema de lazo cerrado compuesto
por un amplificador y una red de realimentación (que
contendría al cristal) que determina la frecuencia de
operación. En la Figura 1 se puede apreciar un
esquema simplificado del sistema.
Usando algebra de bloques se puede
encontrar la transferencia de lazo cerrado como,
v o (s)
A
?
v i (s ) 1 ? ? (s ) A
(1)
Para obtener una oscilación automantenida,
debe haber salida sin excitación externa. Lo anterior
es posible sólo cuando el denominador de (1) se
anula. Por consiguiente la frecuencia y amplitud de
oscilación deben responder a,
vi(s)
+
A
vo(s)
? (s)?
Figura 1. Diagrama en bloques de un oscilador.
1 ? ? ( j? )A ? 0
(2)
A esta última ecuación se la llama criterio de
oscilación de Barkhausen [2]. Si el bloque de
realimentación cumple con esta última condición,
entonces el sistema tendrá polos de lazo cerrado
sobre el eje imaginario del plano s.
Para lograr que el oscilador comience a
funcionar se deberá cumplir ? (j? o)A>1 (los polos de
lazo cerrado se mueven un poco hacia el semiplano
derecho), siendo fo = ? o/2? la frecuencia de
oscilación, la amplitud de la señal de salida crecerá
hasta el punto en el que las nolinealidades del
amplificador hagan decrecer la ganancia de lazo a la
unidad (los polos de lazo cerrado vuelven a estar
sobre el eje imaginario). La frecuencia de oscilación
fo se ajusta sola de manera que el desfasaje total
alrededor del lazo sea de 0° o 360°.
La ecuación compleja (2) se separa en parte
real e imaginaria. La parte real brinda una expresión
para obtener la ganancia del amplificador (o
equivalentemente su transconductancia gm) requerida
para la oscilación, mientras que la parte imaginaria da
una expresión para obtener la reactancia del cristal
necesaria para cumplir la condición de fase para la
oscilación.
Como el sistema resulta ser no lineal las
ecuaciones, en general, no dan resultados muy
exactos. Debido a esto es aconsejable hacer un diseño
en forma conjunta con las ecuaciones y una
contraparte experimental.
Existen varios métodos para diseñar
osciladores a cristal [1]. El que será uasdo aquí es el
de los parámetros admitancia. Previo a comenzar con
el método de diseño se obtendrá un modelo con el
cual poder representar al resonador de cristal de
cuarzo.
2. MODELO DEL CRISTAL DE CUARZO
Un resonador de cristal de cuarzo utiliza las
propiedades piezoeléctricas del cuarzo. Este se
compone de un trozo de cristal ubicado entre dos
electrodos. Una tensión alterna aplicada a estos
electrodos produce una vibración en el cristal. Si la
frecuencia de esta tensión es muy cercana a la
resonancia mecánica del trozo de cuarzo, la amplitud
de la vibración se vuelve muy grande. La impedancia
efectiva que hay entre los electrodos depende
fuertemente de la frecuencia de excitación y posee un
Q extremadamente alto.
Eléctricamente, el cristal de cuarzo puede
ser representado por el esquemático simplificado de
la Figura 2.
Rc, Lc y Cc representan el cuarzo y Co
representa la capacidad entre los electrodos en
paralelo con la capacidad del contenedor del
resonador. La inductancia Lc es una función de la
masa del cuarzo mientras que Cc está relacionado con
su rigidez. La resistencia Rc resulta de las pérdidas
del cuarzo y del arreglo del montaje. Todos estos
parámetros pueden ser medidos con bastante buena
exactitud, por ejemplo con un voltímetro vectorial.
En la Figura 3 se puede apreciar un gráfico de la
reactancia y la resistencia equivalente del cristal en
función de la frecuencia para un cristal de 2 MHz
típico. La impedancia del cristal cambia tan
rápidamente con la frecuencia que cualquier otro
componente del circuito puede ser considerado de
reactancia constante. Los valores de los elementos
del modelo del cristal graficado en la Figura 3 son,
(a)
(b)
Figura 2.
(a) Representación circuital de un
cristal de cuarzo; (b) Impedancia equivalente de un
cristal de cuarzo.
frecuencia difiere un poco de fs debido a la presencia
de Co, pero para fines prácticos puede ser considerada
igual. La frecuencia marcada como fL es en la cual el
cristal resuena con una capacidad externa CL=50pF.
Si definimos ? f = fL - fs, se puede obtener,
Cc
?f
?
(6)
fs
2 (C o ? C L )
Por último, la frecuencia llamada fp es la
frecuencia de resonancia paralelo del cristal con la
10
x 10
5
Re
Xe
5
.
0
fp
Rc = 153 ? ; Lc = 718 mH; Cc = 8,82 fF; Co = 7 pF
Resistencia y reactancia del cristal
Siendo la reactancia y la resistencia
equivalente del cristal,
Re ?
Xe ?
R cXo
2
R c ? (X c ? X o )
2
-5
2.0002
2.0004
(3)
2
X o [R c ? X c (X c ? X o )]
2.0006
2.0008
frecuencia [Hz]
2.001
6
x 10
(a)
2
R c ? (X c ? X o )
2
2
(4)
7000
6000
5000
1
donde: X o ? ?
? Co
y
Xc ? ? Lc ?
4000
3000
1
? Cc
1/(2 ? f CL)
2000
1000
0 del cristal
Reactancia
Hay varias frecuencias marcadas en la figura
3-b. fs es la frecuencia a la cual el cristal es resonante
serie y está dada por,
fs ?
1
2? L c ? C c
(5)
La segunda frecuencia que se aprecia es fr, a
la cual el cristal es puramente resistivo; esta
..
fs
fr
.
fL
-1000
-2000
-3000
1.9993 1.9994 1.9995 1.9996 1.9997 1.9998 1.9999
frecuencia [Hz]
2
2.0001 2.0002
x 10
6
(b)
Figura 3. (a) Variaciones de la resistencia y reactancia del
cristal en función de la frecuencia; (b) Reactancia del cristal
alrededor de la frecuencia de resonancia serie del cristal.
capacidad de su contenedor Co. Esta frecuencia está
dada aproximadamente por,
?
Cc ?
f p ? f s ?1 ?
?
2C o ?
?
excepto aquel para el cual el denominador también es
cero; en ese caso V es indeterminado. Sin embargo,
se sabe que para que exista la oscilación V debe ser
distinto de cero y por consiguiente se debe cumplir
(7)
Normalmente un cristal es utilizado entre la
frecuencia de resonancia serie y la de resonancia
paralelo de manera que su reactancia equivalente sea
inductiva [1].
ADMITANCIA
Se puede derivar la ecuación compleja que
determina las condiciones de oscilación usando el
digrama en bloques de la Figura 4, en el cual el
elemento activo está representado por sus parámetros
Y (o de admitancia), y la red de realimentación está
representada por sus parámetros Z (o de impedancia).
Planteando mallas se tiene,
I = y11 V + y12 V’
I’= y21 V + y22 V’
(8)
V’= -z11 I’- z12 I
V = -z21 I’– z22 I
Resolviendo estas ecuaciones utilizando el
método de determinantes para despejar V se obtiene
(9).
0 y 12 ? 1 0
0 y 22
0
?1
0 1 z12 z11
0 0 z 22 z 21
V?
(9)
y 11 y 12 ? 1 0
y 22
1
0
z12
?1
z11
1
0
z 22
z 21
El numerador de la expresión anterior es
igual a cero, haciendo V = 0 para cualquier caso
I
I’
y11 y12
V
-I
z11 z12
V
V’
y21 y22
z21 z22
Figura 4. Diagrama en bloques de un oscilador.
y 12
?1
0
y 21
y 22
0
?1
0
1
1
0
z12
z 22
z11
z 21
? 0
(10)
Resolviendo este determinante se obtiene la
ecuación:
3. MÉTODO DE LOS PARÁMETROS
y 21
0
y 11
y21 z21 + y11 z22 + y22 z11 + y12 z12 + ? y ? z + 1 = 0
(11)
donde
? y = y11 y22 – y21 y12
? z = z11 z22 – z21 z12
Esta ecuación es muy general y puede ser
aplicada a casi cualquier oscilador. Se puede
representar el elemento activo por sus parámetros Y y
la red de realimentación por sus parámetros Z, o
viceversa.
Es importante destacar que el uso de los
parámetros de dos puertos implica que el
amplificador es lineal. Teniendo en cuenta esto
último, la ecuación (9) no puede brindar información
acerca de la generación de armónicos o la limitación
de la amplitud como resultado de la dependencia de
los parámetros con la amplitud. Para el caso de
grandes amplitudes, los parámetros Y deben ser
definidos
como
razones
de
componentes
fundamentales de corriente a componentes
fundamentales de tensión.
4. DISEÑO DEL VCXO
Los osciladores Pierce, Colpitts y Clapp [1]
tienen la misma configuración circuital, pero con la
tierra de señal en diferente posición. En el oscilador
Pierce la tierra está en el emisor, en el Colpitts en el
colector y en el Clapp en la base. En un circuito
práctico las capaciadades parásitas y los resistores de
polarización aparecen en paralelo de diferentes
elementos para cada una de las tres configuraciones
haciendo que cada una se desempeñe de distinta
manera. En la Figura 5 se puede observar un
esquemático que sirve para representar las tres
configuraciones.
Aunque hasta ahora se ha hablado de
osciladores y no de osciladores controlados por
tensión, el análisis también se aplicará a este caso
pues para variar la frecuencia de oscilación del
circuito se puede agregar un capacitor controlable por
tensión, en serie con el cristal. Para lograr esto se
puede utilizar un diodo varicap. También hará falta
agregar una resistencia de valor elevado para separar
la tensión de control y que el circuito no la considere
como un cortocircuito en señal.
En el presente trabajo se hará uso de la
configuración Colpitts, puesto que en ella uno de los
terminales del cristal está a tierra permitiendo poner
el ánodo del diodo varicap directamente a dicho
potencial. En la Figura 6 se pueden apreciar las
consideraciones circuitales antes mencionadas.
En la Figura 7 aparece el circuito utilizado
en el diseño, junto con sus versiones de polarización
y de señal.
?
gm>>
1
RE
Entonces los parámetros Y simplificados del
amplificador quedan:
yi ?
1
? j? C ?
r?
(12-a)
Cálculo de los parámetros Y del amplificador
En la Figura 8 se puede observar el modelo
? -híbrido del transistor bipolar en colector común
[3], incluyendo además las resistencias de
polarización y de carga.
Antes de comenzar haremos algunas
aproximaciones para simplificar el circuito: ro y r?
son de valor muy elevado, y rbb’ es de pequeño valor,
por lo tanto no serán tenidas en cuenta en el diseño.
El circuito simplificado aparece en la figura 8-b.
Planteando mallas en el circuito simplificado
de la Figura 8-b y teniendo en cuenta las siguientes
simplificaciones:
a) C? >>C? .
b) las resistencias de polarización, por lo
general se eligen de gran valor para poder
considerarlas despreciables frente a la resistencia de
entrada del transistor:
1
1
?
??
r?
R th
1 gm
?
, pues ? o es
r?
?o
al menos del orden de las de las decenas.
c) ? o=gmr?
?
gm>>
(a)
(b)
(c)
Figura 7.
Circuito del oscilador Colpitts a
diseñar: (a) circuito completo; (b) circuito
simplificado de polarización; (c) circuito
simplificado de señal.
C?
(a)
b
Rth
r?
rbb’
C?
R?
c
Figura 5.
Diagrama esquemático
básico de señal de los osciladores
Pierce, Colpitts y Clapp.
r?
b
c
d) si RE es del orden de los k? y gm del
orden de las decenas de mS
ro
C?
RE
c
C?
Rth
Figura 6. Agregado circuital para lograr el
VCXO.
v?
gmv?
e
e
v?
gmv?
RE
(b)
c
Figura 8. Circuito de pequeña señal del amplificador:
(a) circuito completo, modelo ? -híbrido del transistor
bipolar con la inclusión de las resistencias de
polarización; (b) circuito simplificado de pequeña señal
para el amplificador.
yr ? ?
1
? j? C ?
r?
(12-b)
yf ? - gm - j? C?
(12-c)
yo ? gm + j? C?
(12-d)
I1
C2
Re
V1
C1
? y = yi yo – yf yr = 0
Figura 9. Red de realimentación del VCXO.
Cálculo de los parámetros Z de la red de
realimentación
En la figura 9 está representado el circuito
de la red de realimentación.
z r ? z12 ?
z f ? z 21 ?
z o ? z 22 ?
V1
I2
?
I2 ? 0
X 2 (? X e '? jR e )
Z
?
I1 ? 0
V2
I1
V2
I2
?
I2 ? 0
?
I1 ? 0
Siendo:
1
Xe '? Xe ?
y
? Cd
X 2 (? X 1 ? X e '? jR e )
Z
X 2 (? X e '? jR e )
? zr
Z
? 1
? ?? ? j? C ?
? r?
? R e ? j(X1 ?
?
? X 2 (? X e '? jR e ) ?
?
?
X 2 ? X e ') ? 0
El próximo paso es separar la ecuación
compleja anterior en parte real e imaginaria.
Sus parámetros Z están dados por:
V1
I1
V2
Le ’
Debido a la simetría de las ecuaciones
anteriores el parámetro ? y se anula.
z i ? z11 ?
I2
(13-a)
(13-b)
(13-c)
(X 1 ? X 2 )(? X e '? jR e )
(13-d)
Z
Z = Re + j(X1+X2+Xe’)
Además podemos calcular ? z como:
X X
? z ? z i z o ? z f z r ? ? 1 2 2 (R e ? jX e ' )
Z
Derivación de las ecuaciones de diseño
Multiplicando (11) por Z y reemplazando
los parámetros ya calculados, la ecuación se
convierte en:
? (g m ? j? C ? )X 2 (? X e '? jR e ) ?
? 1
?
? ?? ? j? C ? ?? (X1 ? X 2 )(? X e '? jR e ) ?
? r?
?
? (g m ? j? C ? )X 2 (? X 1 ? X e '? jR e ) ?
Parte real:
De la parte real, simplificando y
reagrupando se obtiene:
XX '
g m X1X 2 ? 1 e ? ? C ? R e X1 ? R e
(14)
r?
El signo mayor igual aparece porque la
ganancia inicial del amplificador debe ser mayor a la
ganancia de oscilación estable para que el circuito
comience a oscilar, como fue mencionado
anteriormente.
Parte imaginaria:
Nuevamente, simplificando y reagrupando:
R
X1 ? X 2 ? X e ' ? ? e X 1 ? ? C ? X 1 X 2 ? ? C ? X 1 X e '
r?
(15)
Las ecuaciones obtenidas son de la forma:
g m X1 X 2 ? R e ? K 1
(16)
X1 ? X 2 ? X e ' ? 0 ? K 2
(17)
1
.
? C
Despejando Xe’ de (15) y reemplazando en
(14) se obtiene:
Haciendo C1=C2=C, X 1 ? X 2 ? X ? ?
g m ? R e (? C ) 2 ?
1
1
r? ?
C ?
?1? ? ?
C ?
?
?
R
C
?2? e ? ?
?
r?
C
?
?
? ? ? 2 C ? CR e
?
?
(18)
Ahora, despejando el valor de capacidad del
diodo varicap de (15) se consigue la ecuación (19).
Cd ?
1
1
? Xe ?
(C ? C ?
?
R
C ?
? 2? e ? ? ?
) ??
r?
C ??
(19)
Con las ecuaciones (18) y (19), el VCXO
puede ser diseñado para un dado cristal, una dada
capacidad C y un dado transistor.
Como el circuito deberá oscilar en cierto
rango de frecuencia, (18) y (19) se deberán cumplir
en todo ese rango. Se puede ver de (16) que la peor
condición para la elección de gm se dará a la mayor
frecuencia de oscilación, por lo que todo el
procedimiento siguiente se deberá realizar para la
máxima frecuencia de operación.
Primero, se realiza un cálculo inicial de gm
con (16) considerando K1 nula. Luego, el valor
obtenido de gm se utiliza para calcular los parámetros
aproximados del transistor a utilizar. Con (18) se
calcula un nuevo valor de gm que se utiliza para
recalcular los parámetros del transistor y reemplazar
otra vez en (18). Iterando de esta manera, se llega a
una condición en la que gm(n+1)=gm(n). Una vez
obtenido el valor de transconductancia se elige un
valor gmo, que es 2 a 3 veces la calculada (ya que este
valor da buenos resultados en la práctica). Ahora con
la ayuda de (19) se calculan las capacidades máxima
y mínima del diodo para que el circuito oscile a las
frecuencias mínima y máxima, respectivamente.
Con el valor de gmo obtenido se calcula la
corriente de colector de polarización necesaria.
Ahora, teniendo en cuenta el circuito de polarización
de la Figura 8-b se pueden plantear las siguientes
ecuaciones:
IC
[R th ? (? ? 1)R E ]
?
VCC = VCE – IC RE
Vth ? VBE ?
(20)
(21)
Fijando un punto de trabajo para un dado
valor de VCE y eligiendo Rth por lo menos 10 veces
mayor a r? sólo restan calcular los valores de las
resistencias Ra, Rb y RE (considerando una tensión de
alimentación dada).
Si las condiciones para la oscilación son
satisfechas, la amplitud de oscilación empieza a
crecer hasta que los efectos no lineales reducen la
ganancia efectiva del lazo a la unidad.
En un oscilador a transistor, la nolinealidad
predominante ocurre debido al corte de la juntura
base-emisor durante parte del ciclo. Bajo ciertas
condiciones de polarización puede ocurrir la
saturación de colector. Generalmente, la saturación
de colector tiende a incrementar la dependencia del
oscilador con la tensión de alimentación y por
consiguiente se trata de evitar [1].
Una vez que el circuito esté oscilando de
manera estable, la transconductancia de gran señal
(definida como razón de componentes fundamentales
de corriente y tensión) será igual al gm calculado. Con
0
10
o
m
/m
g
-1
10
Factor de transconductancia g
-2
10
10
-1
0
10
10
1
10
2
V=qE/(kT)
Figura 10. Relación entre la transconductancia de gran
señal y la de pequeña señal.
la transconductancia de pequeña señal requerida para
la oscilación gm y la de pequeña señal inicial gmo (2 a
3 veces gm) se puede calcular la razón gm/gmo y
obtener de la Figura 10 la tensión base-emisor
normalizada V, considerando que se produce el corte
de la juntura base-emisor durante parte del ciclo. La
tensión base-emisor es E=V kT/q (siendo
kT/q=26mV a 25°C). La curva de la Figura 10
responde a la ecuación:
gm
2 ? I1 (V )
?
g mo V ? I 0 (V )
En la ecuación anterior Ii representan
funciones de Bessel modificadas de primer tipo [1].
Una vez obtenida la tensión en la base es
fácil obtener la tensión en las otras partes del circuito.
Si el oscilador estuviera polarizado de
manera de producir limitación por colector, la tensión
de salida puede ser determinada construyendo una
recta de carga como se muestra en la Figura 11. La
tensión de salida será, aproximadamente, V1 o V2, la
menor de las dos.
IC
Q
V1
V2
VCE
Figura 11. Predicción de la tensión de salida del
oscilador a partir del punto de trabajo del transistor
Q y de la recta de carga.
6. CONSIDERACIONES PARA LA
INTEGRACIÓN
En vistas a implementar un VCXO en forma
integrada, varios factores deben ser tenidos en cuenta.
Como una primera consideración, los límites
máximos para resistencias y capacitores integrados
está en el orden de los 100k? y 100pF,
respectivamente.
Las resistencias pueden ser sintetizadas
usando un Layer especial de polisilicio de alto grado
óhmico (HIPO) en las tecnologías que lo posean.
También pueden ser integradas con el Layer de Pozo
(R?? 2k? / ?).
Los capacitores pueden ser construídos por
la superposición de 2 Layers de metal o de polisilicio.
Otro aspecto de importancia son las dimensiones del
transistor usado en este tipo de configuración. En
virtud de que la transconductancia de los BJT es
aproximadamente un orden de magnitud mayor que
la de los MOST, quizás sea conveniente el uso del
primer tipo de transistor. Como contraparte, el costo
de las tecnologías BJT o BiCMOS son elevados
cuando son comparados frente al costo de una
tecnología MOS. Mas aún, el poder integrar en
tecnología MOS habilita al circuito a poder formar
parte de estrcucturas mixtas (analógico-digitales)
MOS, como es la tendencia actual.
La topología empleada es similar en el caso
de un circuito realizado enteramente en MOS, pero
teniendo en cuenta ahora la expresión cuadrática de
los mencionados dispositivos. Si se usan MOST en
conducción subumbral, los resultados teóricos
obtenidos se mantienen sin cambio, en virtud de la
característica exponencial de los dispositivos en esta
zona de operación.
A fin de conformar el diodo varicap, una
juntura inversamente polarizada puede ser utilizada,
por lo que su construcción no reviste mayor
inconveniente a la hora de elegir una tecnología de
integración.
(a)
(b)
Figura 12. Pantallas de osciloscopio mostrando la salida
del protoptipo discreto de VCXO: (a) frecuencia 2MHz; (b)
frecuencia 2,0004MHz.
hace para la mayor frecuencia de operación por lo
que para la menor frecuencia, el valor de
transconductancia está sobredimensionado y debido a
esto el contenido armónico será mayor [1]. Sin
embargo, es usual colocar un comparador a la salida
del circuito de manera de salvar esta diferencia en la
forma de onda al variar la frecuencia, así como
también eliminar toda modulación de amplitud.
7. RESULTADOS EXPERIMENTALES
8. CONCLUSIONES Y TRABAJO FUTURO
A fin de validar el procedimiento de diseño
presentado, a continuación se muestran los resultados
obtenidos con la implementación de un prototipo
discreto.
Para la obtención de los valores de los
dispositivos empleados, un software de uso comercial
fue usado a fin de implementar el algoritmo descripto
en el item 4.
En la Figura 12 es mostrada la salida del
circuito trabajando a dos frecuencias distintas, usando
el cristal de la Figura 3. Los valores calculados se
corresponden
bien
con
los
obtenidos
experimentalmente. En la mencionada Figura se
puede apreciar que para la mayor de las frecuencias
la forma de onda es más similar a una sinusoide. Esto
se debe a que la elección de la transconductancia se
El análisis de un VCXO ha sido presentado.
El proceso de aproximaciones para el cálculo de los
dispositivos, en forma iterativa, demuestra ser
eficiente. Aunque el diseño explicado en el item 4 es
para un caso particular (con sus respectivas
aproximaciones), el procedimiento no pierde
generalidad para otro tipo de dispositivo o tecnología.
Resultados obtenidos de un prototipo discreto son
dados validando lo anterior. Trabajo futuro es la
integracion en silicio de 2 prototipos en tecnología
MOS de bajo costo: uno trabajando en inversión
débil, con propósitos de baja potencia consumida, y
otro para mayor frecuencia de operación con los
MOST trabajando en el régimen de inversión fuerte.
9. AGRADECIMIENTOS
Agradezco a los Ing. Hugo Lorente y
Gerardo Sager por su ayuda y colaboración para que
este trabajo pudiera ser realizado.
Quiero hacer un agradecimiento especial a
José Luis Ceballos por su apoyo y ayuda con respecto
de las consideraciones de integración.
10. REFERENCIAS
[1] Frerking, Marvin. “Crystal oscillator design and
temperature compensation”, Van Nostrand Reinhold
Company, 1978.
[2]
Strauss, Leonard. “Wave Generation and
Shaping”, Mc Graw Hill Book Company, 1960.
[3] Ph.D. Millman, Jacob. Sc.D. Grabel, Arvin.
“Microelectrónica”, Editorial Hispano Europea,
1991.