EL “MODO ARRASTRE”1 El principal atributo de Cabri
Anuncio
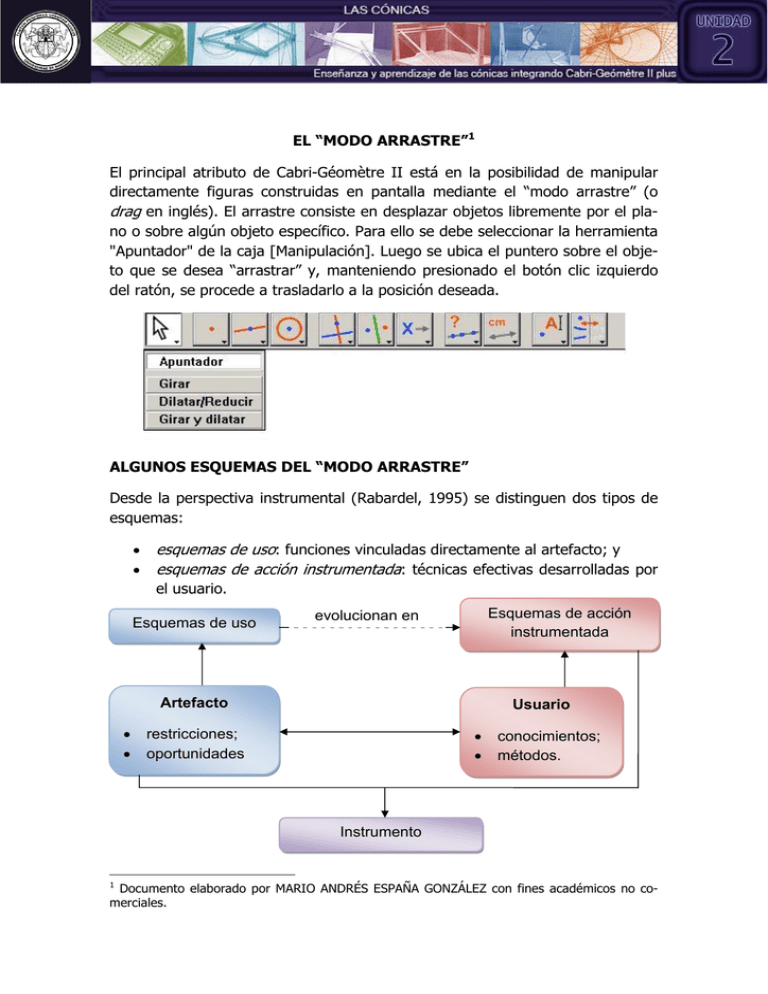
EL “MODO ARRASTRE”1 El principal atributo de Cabri-Géomètre II está en la posibilidad de manipular directamente figuras construidas en pantalla mediante el “modo arrastre” (o drag en inglés). El arrastre consiste en desplazar objetos libremente por el plano o sobre algún objeto específico. Para ello se debe seleccionar la herramienta "Apuntador" de la caja [Manipulación]. Luego se ubica el puntero sobre el objeto que se desea “arrastrar” y, manteniendo presionado el botón clic izquierdo del ratón, se procede a trasladarlo a la posición deseada. ALGUNOS ESQUEMAS DEL “MODO ARRASTRE” Desde la perspectiva instrumental (Rabardel, 1995) se distinguen dos tipos de esquemas: esquemas de uso: funciones vinculadas directamente al artefacto; y esquemas de acción instrumentada: técnicas efectivas desarrolladas por el usuario. Esquemas de uso Esquemas de acción instrumentada evolucionan en Artefacto Usuario restricciones; oportunidades conocimientos; métodos. Instrumento 1 Documento elaborado por MARIO ANDRÉS ESPAÑA GONZÁLEZ con fines académicos no comerciales. A este proceso evolutivo, que conduce a la construcción de instrumentos, se le llama génesis instrumental (Trouche, 2005). Soury-Lavergne (2008), propone la siguiente lista de posibles esquemas en la génesis instrumental del arrastre para la validación de construcciones: Esquemas de uso Hacer clic en el icono de puntero y soltar el botón; distinguir los puntos que pueden ser arrastrados de los otros; y mantener presionado el botón derecho del ratón y moverlo en diferentes direcciones. Esquemas de acción instrumentada Elegir los objetos adecuados para efectuar el arrastre; identificar perceptualmente el hecho geométrico que se debe comprobar; decidir si se conserva o no; y concluir si el hecho geométrico es una propiedad de la figura o no. TIPOS DE ARRASTRE El arrastre puede ser utilizado para varios fines y en distintos momentos, todo depende de la estructura cognitiva que oriente la acción del estudiante. En efecto, Arzarello y otros (2002), a partir de sus propias experiencias, han logrado detectar varios modos de arrastre. Siguiendo estas investigaciones, Gutiérrez (2005) destaca como más útiles los siguientes tipos: Tipo Arrastre de test Arrastre errático Descripción Consiste en arrastrar puntos u objetos básicos de un diagrama construido para comprobar si las condiciones iniciales del problema se conservan con la variación. Consiste en arrastrar aleatoriamente puntos u objetos básicos con el propósito de encontrar invariantes o regularidades, sin disponer de una idea previa que oriente la exploración. Arrastre guiado Arrastre sobre un lugar geométrico oculto Consiste en arrastrar puntos u objetos básicos a fin de obtener una configuración particular del diagrama construido. Consiste en acotar el dominio de variación de un punto cuando es arrastrado, esto con el fin de preservar una propiedad descubierta. Generalmente, la trayectoria del punto coincide con un lugar geométrico oculto, incluso sin ser consciente de ello. Ejemplo: Construir el foco y la directriz de una parábola dada. BIBLIOGRAFÍA Arzarello, F., Olivero, F., Paola, D. & Robutti, O. (2002). A cognitive analysis of dragging practices in Cabri environments. Zentralblatt für Didaktic der Mathematik, 34 (3), 66-72. Gutiérrez, A. (2005): Aspectos metodológicos de la investigación sobre aprendizaje de la demostración mediante exploraciones con software de geometría dinámica. En A. Maz; B. Gómez & M. Torralbo, (Eds.). Actas del 9º Simposio de la Sociedad Española de Investigación en Educación Matemática. (pp. 27-44). Córdoba, España: Universidad de Córdoba. Rabardel, P. (1995). Les hommes et les technologies: approche cognitive des instruments contemporains. Paris, Francia: Arman Colins. Soury-Lavergne, S. (2008). Deductive reasoning and Instrumental genesis of the drag mode in dynamic geometry. ICMI 11 International Congress on Mathematical Education - TSG 22. Monterrey, México: UANL. Trouche, L. (2005). An instrumental approach to mathematics learning in symbolic calculator environments. En D. Guin, K. Ruthven y L. Trouche (Eds.). The didactical challenge of symbolic calculators. (pp. 137-162). Dordrecht, NL: Springer.