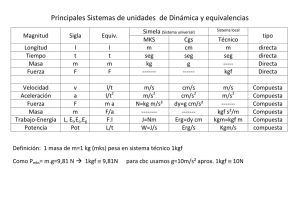
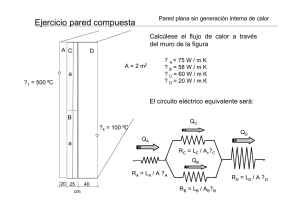
Definición de función compuesta

Definición de función compuesta
La función compuesta f g, de dos funciones, f y g se define
mediante
(f g)(x) = f(g(x)).
El dominio de f g es el conjunto de todas las x en el dominio
de g, tales que g(x) esté en el dominio de f.
La figura que está a continuación es un esquema que muestra las
relaciones entre f g y f g.
Nótese que para x en el dominio de g, primero se determina g(x)
(la cual debe estar en el dominio de f ) y después se determina f(
g(x)).
Para la función compuesta g f, se invierte este orden, calculando
primero f(x) y después g(f(x)). El dominio de g f es el conjunto
de todas las x en el dominio de f tales que f(x) esté en el dominio
de g.
Como la notación g(x) se lee "g de x", a veces se dice que g es
una función de x. Para la función compuesta f g, la notación
f(g(x)) se lee "f de g de x," y se considera que f es función de g(x).
En este sentido, una función compuesta es una función defunción,
o, con más propiedad, una túnción de los valores de otra función.