x A B C D y a b
Anuncio

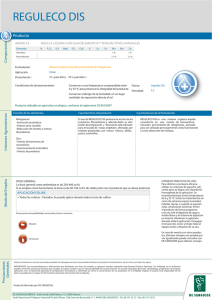
Escuela Técnica Superior de Ingenieros de Caminos, Canales y Puertos (Madrid) Método de los Elementos Finitos (Curso 07-08) EJERCICIO 2: Modelos de potencial Fecha lı́mite de entrega: lunes 3 de diciembre diciembre 1. Se considera el problema de contorno unidimensional definido por las siguientes ecuaciones: d2 u − p(p − 1)xp−2 = 0, 2 dx du =0 dx x=0 u(1) = 1 0<x<1 (1) (2) (3) siendo p una constante dada. Se pide: 1. Obtener la solución exacta de este problema para p = 5, y representarla gráficamente. 2. Expresar la formulación débil del problema de contorno. 3. Expresar la formulación de Galerkin. 4. Expresar la formulación matricial. 5. Resolver “a mano” la formulación matricial del problema de elementos finitos del apartado anterior para p = 5, utilizando funciones de forma lineales y considerando las siguientes discretizaciones: a) un único elemento. b) dos elementos iguales. 6. Comparar el valor exacto de la derivada de u en x = 1 con los valores aproximados obtenidos en el apartado anterior. Justificar porqué los resultados numéricos no aproximan correctamente el resultado analı́tico. 2. Una placa conductora rectangular, de lados a = 4 m. y b = 2 m., tiene las temperaturas impuestas en sus cuatro lados de acuerdo con las expresiones (ver la figura adjunta): TAB = TBC = TAD = T0 TCD (x) = T0 x(a − x) + T0 T0 = 100◦ C y D a C b x A B Considerando que la placa se encuentra en régimen estacionario, realizar un modelo de elementos finitos que permita calcular la distribución de temperaturas en la placa y comparar los resultados obtenidos con la solución analı́tica: Z a ∞ X 2 senh(λn y) T (x, y) = T0 + sen(λn x) T0 x(a − x) sen(λn x) dx a senh(λ b) n 0 n=1 πn λn = a