Diapositivas TEMA II parte II
Anuncio

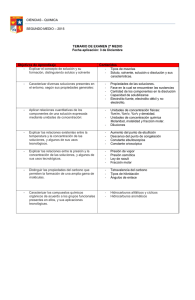
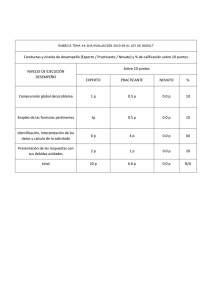
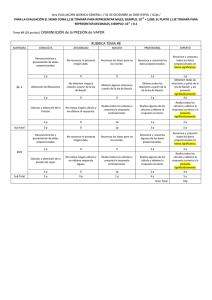
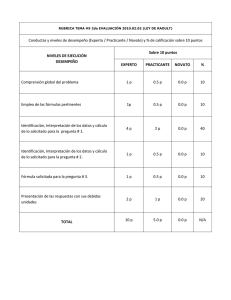
EQUILIBRIO DE FASES Equilibrio Líquido-Vapor de soluciones binarias, en el sentido de la Ley de Raoult La representación tridimensional de los sistemas de equilibrio binario puede ser difícil de analizar por lo que podemos analizar estos sistemas a partir de su representación en el plano, realizando cortes a Temperatura constante, obteniendo gráficos P vs. XY y a Presión constante, obteniéndose diagramas T vs. XY. Los diagramas de Equilibrio se basan en las siguientes premisas • Se toma como componente uno (1) el componente más volátil • El eje de las abscisas contendrá tanto los datos de la composición del vapor como el de líquido. • El eje de las composiciones ira de 0 a 1 respecto al componente 1 de izquierda a derecha y para el componente 2 de 0 a 1 de derecha a izquierda • En el eje de las Ordenadas ira P si la T es constante y T si la P es constante • El componente 1 será el que tiene la Presión de Vapor (Psat) más alta o la Temperatura de Saturación más baja. EQUILIBRIO DE FASES Equilibrio Líquido-Vapor de soluciones binarias, en el sentido de la Ley de Raoult En el Equilibrio L-V se introducen los siguientes términos: zi: Fracción de molar global o promedio de la mezcla del componente i Xi: Fracción molar en la fase líquida yi: Fracción molar en la fase de vapor Para el balance molar de las fases: F: cantidad de moles o flujo molar de la mezcla. L: Cantidad total de moles en la fase líquida V: Cantidad total de moles en la fase de Vapor Por definición: Balance Global F=L+V Balance por componentes ziF=xiL+yiV EQUILIBRIO DE FASES Construcción de Diagramas P vs. XY y T vs. XY para sistemas binarios utilizando la ley de Raoult Diagramas P vs. XY. Procedimiento para la elaboración de un diagrama P vs. XY a T constante. • Como la T es constante calculamos las Pisat de ambos componentes; puede calcularse mediante la ecuación de Antoine 𝐵 𝐿𝐿𝑃𝑖 𝑠𝑠𝑠 = 𝐴 − 𝑇+𝐶 • Asumimos los valores de la composición de la fase líquida del componente más volátil x1 entre 0 y 1. • Calculamos la P del sistema empleando la Ley de Raoult colocándola en función de x1. 𝑦1 𝑃 = 𝑥1 𝑃1 𝑠𝑠𝑠 𝑦2 𝑃 = 𝑥2 𝑃2 𝑠𝑠𝑠 sumando 𝑥1 = 1 − 𝑥2 𝑃 = 𝑥1 𝑃1 𝑠𝑠𝑠 + 𝑥2 𝑃2 𝑠𝑠𝑠 𝑃 = 𝑥1 𝑃1 𝑠𝑠𝑠 − 𝑃2 𝑠𝑠𝑠 + 𝑃2 𝑠𝑠𝑠 EQUILIBRIO DE FASES Construcción de Diagramas P vs. XY y T vs. XY para sistemas binarios utilizando la ley de Raoult • Con cada valor de x1 calculamos la correspondiente presión • Las composiciones de la fase líquida las determinamos por Raoult. 𝑥1 𝑃1 𝑠𝑠𝑠 𝑦1 = 𝑃 • Graficamos x1 vs. P y y1 vs. P, obteniendo las curvas de burbuja y rocío respectivamente Líquido comprimido P1sat Curva de Burbuja L-V Línea de Pliegue Curva de Rocío P2sat Vapor sobrecalentado 0 Z1 X1 X1 Y1 Y1 1 Línea Isopleta EQUILIBRIO DE FASES Construcción de Diagramas P vs. XY y T vs. XY para sistemas binarios utilizando la ley de Raoult Diagramas T vs. XY. Procedimiento para la elaboración de un diagrama T vs. XY a P constante. Dada una presión total P • Calculamos la Tisat para cada componente por Antoine. 𝑇𝑖 𝑠𝑠𝑠 = 𝐵𝑖 − 𝐶𝑖 𝐴𝑖 − 𝑙𝑙𝑙 • Con T1sat y T2sat calculados, asumimos valores en ese rango. • Con cada valor entre T1sat y T2sat, calculamos P1sat y P2sat por Antoine • Suponiendo válida la Ley de Raoult y estableciendo la relación de Presión para 2 componentes: 𝑃 = 𝑥1 𝑃1 𝑠𝑠𝑠 − 𝑃2 𝑠𝑠𝑠 + 𝑃2 𝑠𝑠𝑠 EQUILIBRIO DE FASES Construcción de Diagramas P vs. XY y T vs. XY para sistemas binarios utilizando la ley de Raoult Despejamos x1 y calculamos esta para cada Pisat 𝑥1 = 𝑃 − 𝑃2 𝑠𝑠𝑠 𝑃1 𝑠𝑠𝑠 − 𝑃2 𝑠𝑠𝑠 • Conocidas todas las x1 calculamos y1 por la ecuación de Raoult • Calculamos todos los x1 y calculamos las y1 por Raoult 𝑥1 𝑃1 𝑠𝑠𝑠 𝑦1 = 𝑃 Calculamos y1 a cada x1 y P1sat con P constante. Conocidas x1 para cada T trazamos la curva de burbuja. Conocida y1 para cada T trazamos la curva de rocío. EQUILIBRIO DE FASES Construcción de Diagramas P vs. XY y T vs. XY para sistemas binarios utilizando la ley de Raoult Diagrama T vs. XY Vapor sobrecalentado T2sat Curva de Rocío L-V Curva de Burbuja T1sat Líquido Sub-enfriado 0 X1 X1 Y1 Z1 Y1 1 EQUILIBRIO DE FASES Análisis del comportamiento de un sistema binomial L P1sat C L-V D H G E I J F T , Z1 P2sat V 0 X1H X1J X1 Y1 Z1 Y1I Y1G 1 EQUILIBRIO DE FASES Análisis del comportamiento de un sistema binomial V V2 V1 T1 N T2sat T2 T2 Q L T3 R L-V T3 L2 L1 S L T1 T1sat L Y1 0 X1 Z1 X1 X1 Y1 Y1 1 EQUILIBRIO DE FASES Regla de la Palanca Diagrama T vs. XY V Y1 V Balance global 𝐹 =𝐿+𝑉 F Balance por componente Z1 T2sat L-V A B C L 𝑍𝑖 𝐹 = 𝑋𝑖 𝐿 + 𝑌𝑖 𝑉 Despejando X1 𝐿 𝑦1 − 𝑧1 = 𝑉 𝑧1 − 𝑥1 T1sat L Z1 0 X1 X1 Y1 Y1 1 EQUILIBRIO DE FASES Regla de la Palanca Tomando como punto de apoyo a z1, el brazo opuesto a la composición de la fase cuya cantidad se calcula dividiendo esta por la longitud total de la palanca para obtener la cantidad de dicha fase. Cantidad de líquido Cantidad de vapor 𝑦1 − 𝑧1 𝐵𝐵 𝐿= = 𝑦1 − 𝑥1 𝐴𝐴 𝑧1 − 𝑥1 𝐴𝐵 𝑉= = 𝑦1 − 𝑥1 𝐴𝐴 Nota: Esto se encuentra bajo la base de 1 mol o fracción entre 0 y 1 por lo que hay que calcular la cantidad total del sistema. EQUILIBRIO DE FASES Ejercicio En un papel milimetrado construya el sistema binario, BENCENOTOLUENO A 350 K, suponiendo válida la ley de Raoult ¿Cuál es el punto de Burbuja de una mezcla al 30% peso en benceno de composición global a la temperatura de 350 K? ¿A qué presión debe mantenerse una mezcla al 60% de tolueno para que vaporice un 30%? ¿Cuál es la presión de rocío de una mezcla al 55% de benceno? ¿Cuál es la presión y composición del vapor que se encuentra en equilibrio con un líquido al 80% mol de benceno? Para una presión igual al promedio aritmético de las presiones de saturación y una composición global de 65% determine la relación molar entre las fases. Utilice la regla de la palanca. EQUILIBRIO DE FASES Datos de la Ec. De Antoine Benceno (1) A 13,8858 B 2788,51 C -52,36 Temperatura del Sistema T (K) 350 Tolueno (2) 13,9987 A B 3096,52 C -53,67 𝐵 𝑇 𝐾 +𝐶 más volátil verificado por su peso comparado con el tolueno. P1sat (kPa) 91,5665435 P2sat (kPa) 34,7831696 De la Ley de Raoult 𝑃 = 𝑥1 𝑃1 𝑠𝑠𝑠 − 𝑃2 𝑠𝑠𝑠 + 𝑃2 𝑠𝑠𝑠 𝑥1 𝑃1 𝑠𝑠𝑠 𝑦1 = 𝑃 𝑃𝑆𝑆𝑆 𝑘𝑘𝑘 = 𝑒 𝐴− Escogemos a Benceno como componente 1 debido a que es el Presiones de Saturación 𝑦𝑖 𝑃 = 𝑥𝑖 𝑃𝑖 𝑠𝑠𝑠 Ec. De Antoine X1 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 P(kPa) 34,7831696 40,461507 46,1398444 51,8181818 57,4965192 63,1748565 68,8531939 74,5315313 80,2098687 85,8882061 91,5665435 Y1 0 0,22630532 0,39690877 0,53012209 0,63702321 0,72470717 0,7979285 0,8599928 0,9132696 0,95950181 1 100 Benceno (1)-Tolueno(2) -350K P1sat 90 80 Burbuja P (kPa) 70 60 Rocío 50 40 P2sat 30 0 0,1 0,2 0,3 0,4 0,5 0,6 X1 Y1 Burbuja Rocío 0,7 0,8 0,9 1