Problema 65
Anuncio

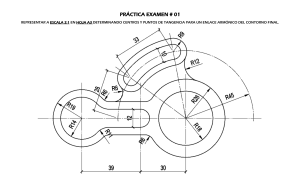
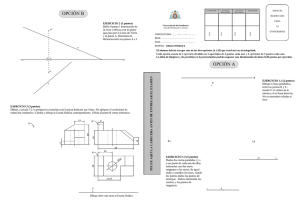
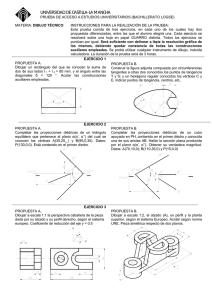
Problema 65 Propuesto por Juan Carlos Salazar, Puerto Ordaz (Venezuela). El cuadrilátero ABCD es bicéntrico (es decir, tiene círculo inscrito y circunscrito); el círculo inscrito tiene centro I y radio r; los círculos exinscritos correspondientes a los lados AB y CD tienen centros y radios (I1 ,r1 ) e (I2 ,r2 ), respectivamente. Los puntos de tangencia del círculo inscrito con los lados AB, BC, CD y DA son, respectivamente, W, X, Y y Z. Los puntos de tangencia de los círculos exinscritos (I1 ,r1 ) e (I2 ,r2 ) con un lado del cuadrilátero y la prolongación de los otros dos, determinan los triángulos “tangenciales exteriores” de áreas S1 y S2 , respectivamente. Demostrar que: i) [WXYZ ] = S1 S r ii) 1 = 1 S 2 r2 r2 r + S2 1 , r1 r2 3/ 2 , donde [ ] representa el área. Z'' C B X I2 Y Z' W I1 I Y' W'' X'' X' A Z D Sean Y', X' y Z' los puntos de tangencia de (I1 ,r1 ) con el lado AB y las prolongaciones de los lados AD y BC, respectivamente, y sean W'', X'' y Z'' los puntos de tangencia de (I2 ,r2 ) con el lado CD y las prolongaciones de los lados AD y BC, respectivamente. Por ser ABCD cíclico, se tiene que: ∠Z ' BY ' = π − ∠ B = ∠D ; ∠X ' AY ' = π − ∠A = ∠C ; ∠X ' ' DW ' ' = π − ∠D = ∠B ; ∠Z ' ' CW ' ' = π − ∠C = ∠ A . Las bisectrices de ∠WBX, ∠XCY, ∠YDZ y ∠ZAW confluyen en I, las de ∠X'AY' e ∠Y'BZ' en I1 , y las de ∠W''DX'' y ∠W''CZ'' en I2 . Por lo tanto, r r CY ∠A AY ' tan = = = 2 ; = r1 AW r CW ' ' 2 r r DY ∠B BY ' tan = = = 2 . = r1 BW r DW ' ' 2 XY W ' ' Z ' ' ∠A X 'Y ' WZ 2 sin = = = ; = r1 AW r CW ' ' 2 ∠B Y ' Z ' WX YZ W ' ' X ' ' 2 sin = = = . = r1 BW r DW ' ' 2 De las anteriores igualdades se obtiene trivialmente que r1 r2 =r2 , y que X 'Y ' Y ' Z ' r1 AY ' BY ' AY '+ BY ' AB = = = = = = ; XY YZ r CY DY CY + DY CD X ' 'W ' ' W ' ' Z ' ' r2 DW ' ' CW ' ' DW ' '+CW ' ' CD = = = = = = . XW WZ r BW AW BW + AW AB Además, AB = AY '+BY ' = r ⋅ r1 r ⋅ r1 ( AW + BW )r ⋅ r1 AB ⋅ r ⋅ r1 + = = ; AW BW AW ⋅ BW AW ⋅ BW XY ⋅ YZ r ⋅r r = = = WX ⋅ WZ AW ⋅ BW r1 AW ⋅ BW = r ⋅ r1 ; r2 . r1 Nos faltan ahora únicamente ciertas relaciones entre ángulos: ∠XYZ = ∠XYI + ∠ZYI = π − ∠XIY π − ∠YIZ ∠C + ∠D + = . 2 2 2 De la misma forma se demuestra que ∠X 'Y ' Z = ∠C + ∠D ; 2 ∠XWZ = ∠X ' 'W ' ' Z ' ' = ∠A + ∠B ∠C + ∠D =π − . 2 2 Podemos entonces decir que S1 [X 'Y ' Z '] = X ' Y '⋅Y ' Z ' sin (∠X 'Y ' Z ') = XY ⋅ YZ r1 = r1 = S 2 [W ' ' X ' ' Z ' '] W ' ' X ' '⋅W ' 'Y ' ' sin (∠X ' 'W ' ' Z ' ') WX ⋅ WY r2 2 r2 2 3/ 2 , q.e.d., y usando este resultado y los anteriores, se tiene que [WXYZ ] = [WXZ ] + [ XYZ ] = WX ⋅ WZ sin (∠ XWZ ) + XY ⋅ YZ sin (∠ XYZ ) 2 2 r W ' ' X ' '⋅W ' ' Z ' ' r X ' Y '⋅Y ' Z ' = 2 sin (∠X ' 'W ' ' Z ' ') + 2 sin (∠ X ' Y ' Z ') 2 2 r2 r1 2 = r2 r1 2 [W ' ' X ' ' Z ' '] + r 2 [ X ' Y ' Z '] = 2 r r = 1 2 r2 r1 q.e.d.. 2 r1 3/ 2 r S1 + 2 r1 r1 r2 3/2 S2 = r1 r S2 + 2 S1 r2 r1 r2 r S1 + 1 S 2 , r1 r2